Introduction
Alpine glaciers make up about 4% of the world’s land ice area (Reference Dyurgerov and MeierDyurgerov and Meier, 1997, 2000). Yet, despite this small fraction, the mass loss of small glaciers accounts for 20–50% of the 10–15cm rise in sea level during the last century (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Reference Kuhn, Warrick and BarrowKuhn, 1993; Reference Meier and BahrMeier and Bahr, 1996; Reference Dyurgerov and MeierDyurgerov and Meier, 1997). Furthermore, small glaciers are highly sensitive to changes in temperature and precipitation (Reference MeierMeier, 1984; Reference OerlemansOerlemans and others, 1998), making them important indicators of regional climate change. Ice loss from alpine glaciers and changes in glacier extent affect alpine ecosystems by altering the watershed hydrology (Reference HallHall, 1994). Variations in glacier mass affect stream-flow volume and timing, which in turn affect hydroelectric power production, irrigation and domestic water supplies (Reference Post, Richardson, Tangborn and RosselotPost and others, 1971; Reference ØstremØstrem, 1973; Reference TangbornTangborn, 1980; Reference Fountain and TangbornFountain and Tangborn, 1985). Therefore, the monitoring of alpine glaciers is also important for resource planning.
To track or estimate glacier volume change requires some kind of monitoring program. Historically, glacier-monitoring programs were based on intensive measurements at each glacier to understand the links between glacier mass balance, meteorology and runoff (Reference Reinwarth and YoungReinwarth, 1993; Reference HolmlundHolmlund, 1996; Reference KrimmelKrimmel, 1999b). However, such intensive measurements were limited to one glacier within a region, with the expectation that those changes represented the processes on all the glaciers across the region. Even if the number of measurements were significantly reduced, monitoring a large number of glaciers is logistically and economically difficult. For many parts of the world, regional glacier inventories have been compiled that depict the distribution and area of individual glaciers at a moment in time (Reference Ommanney, Goodman and MúllerOmmanney and others, 1969; Reference Hagen, Liestøl, Roland and JørgensenHagen and others, 1993; Reference Mool, Bajracharya and JoshiMool and others, 2001). Furthermore, assessment of the temporal change of glacier area over broad regions is extrapolated from a few (often just one) measured glaciers (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Reference Dyurgerov and MeierDyurgerov and Meier, 1997) and applied to these inventories where available. The purpose of our study is to quantify the statistical and topographic characteristics of glacier change over a broad region and to examine the utility of extrapolating that change from a few glaciers. Because the glaciers are shrinking, we also examine the contribution of ice melt to regional stream runoff.
Study Area and Previous Work
The North Cascades National Park Complex, Washington, USA, covers an area of 2757 km2 located at 48º14’–49º N, 120º33′–121º39′ W. The ‘Complex’ refers to the administrative region that includes a national park and two national recreation areas administered by the US National Park Service. It straddles the crest of the northern section of the North Cascade Range, which varies in elevation from <100 m to >2800 m (Fig. 1). The topography is characterized by steep relief with dense forest cover at low to middle elevations and large expanses of exposed rock, snow and ice at upper elevations. Major portions of the complex are alpine and sub-alpine ecosystems, which are conditioned to the water flow from glaciers. Two of the three major watersheds in the complex, Skagit and Stehekin, contain five hydroelectric facilities providing power for several cities including the metropolitan area of Seattle, Washington. The production cycle of these facilities is highly dependent on the timing and volume of stream-flow, which is in turn influenced by patterns of snow and ice melt (Reference TangbornTangborn, 1980). Also, over 600 000 tourists visit the National Park Complex annually (personal communication from J.L. Riedel, 2001) and the glaciers are a major draw. In summary, the timing, magnitude and spatial pattern of glacier shrinkage plays a significant role in the alpine hydrology and ecology, and economy of northwestern Washington State.

Fig. 1. Location of the study area and the distribution of glaciers within it during 1958.
Systematic research of glaciers in the North Cascades dates to the mid-20th century (Reference HubleyHubley, 1956; Reference LaChapelleLaChapelle, 1962). Prior to our study, two inventories of glaciers in the North Cascades were completed. The first is a preliminary census of the glaciers in the contiguous United States that lists 519 glaciers in the entire North Cascade Range (Reference MeierMeier, 1961). The second inventory, by Reference Post, Richardson, Tangborn and RosselotPost and others (1971), identified all ice masses in the North Cascade Range larger than 0.1 km2. They counted 756 glaciers with a combined area of 267 km2. In the late 1950s, a program of intensive measurements began at South Cascade Glacier and included mass change, climate and runoff (Reference MeierMeier, 1961; Reference KrimmelKrimmel, 2000). Other projects in the region have included mapping changes in glacier termini on Mount Baker (Reference HarrisonHarrison, 1970; Reference HarperHarper, 1992) and measuring terminus positions and net mass balance on 47 other glaciers spread throughout the range (Reference PeltoPelto, 1988; Reference Pelto and RiedelPelto and Riedel, 2001). Beginning in 1993, the US National Park Service began a program of annually monitoring four glaciers in the National Park Complex (Riedel and others, 2002).
Glacier Area
Methods
Reference Post, Richardson, Tangborn and RosselotPost and others (1971) used vertical and oblique aerial photography acquired in the late 1950s and 1 : 38 000 scale planimetric maps, produced by the US Forest Service, to create their glacier inventory. Based on their glaciological expertise, they modified the maps by eliminating seasonal snowpatches that biased glacier outlines and deleting isolated snowpatches to preclude misidentification as unique glaciers. From these data they compiled a catalog of glacier characteristics including area, length, average elevation, location (latitude/longitude) and type (e.g. alpine, cirque). Because of their expertise we presume that they developed the best possible inventory of glaciers for that region at that time. However, the authors smoothed the boundaries of the glaciers, making a one-to-one comparison with a future inventory of glaciers problematic.
To provide a basemap of glacier extent, we used a Geographic Information System (GIS) to compile the topographic attributes of the glaciers and to calculate glacier changes. We used 1 : 24 000 scale United States Geological Survey (USGS) topographic maps, which are compiled from aerial photography captured in 1958. Although several map revisions have been produced since 1958, the revisions are limited to changes in man-made structures (e.g. roads) or in major landforms, whereas glacier extent and topography were not updated (personal communication from I. Land-graf, 2000). We tested this assertion by acquiring the original aerial photography (August 1958) for several maps published in the 1990s and found that indeed the glacial extents in the photography matched that depicted on the ‘revised’ maps. After the glacier outlines for 1958 were digitized, they were superimposed on a 30m resolution digital elevation model (DEM) from which the topographic characteristics (maximum, minimum and average elevation, average orientation and average slope) were calculated. Because the photography used for the USGS maps dated to the same time period as those used by Reference Post, Richardson, Tangborn and RosselotPost and others (1971), we could test the accuracy, in a general way, of our inventory.
A second glacier coverage was produced from unrectified color vertical aerial photography (1:12 000 scale) acquired in August 1998. Because georectification of the large number of photographs was prohibitively expensive, we modified the 1958 glacier outlines by superimposing them on the DEM to mimic the shadows observed in the 1998 photography and adjusted the outlines to match the 1998 position relative to landmarks in the photography and on the shaded DEM. This strategy adapted Reference LaChapelleLaChapelle’s (1962) method with hard-copy aerial photographs. Early in the project, we investigated using Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) imagery (Reference Mool, Bajracharya and JoshiMool and others, 2001; Reference Kääb, Paul, Maisch, Hoelzle and HaeberliKääb and others, 2002; Reference Yang, Ding, Chen, Liu and LuYang and others, 2003; Reference BolchBolch, 2004), but its 15 m resolution was too coarse for the small cirque glaciers (> 0.5 km2) common to our study region. We could not use Shuttle Radar Topography Mission (SRTM) data to update glacier topography because 14% of the glacier area is missing due to layover and radar shadowing in steep terrain. Furthermore, the data were collected in February (2000), when snowpack can be as much as 5 m thick and is customarily wet. C-band synthetic aperture radar (SAR) does not penetrate wet snow. Consequently, the topography was not updated, and only glacier area could be determined for the 1998 coverage. To quantify possible non-climatic influences on glacier change we quantified debris-covered area on affected glaciers in the 1998 coverage, and for both coverages we measured the distance from the glacier to any nearby lake. Although the glaciers in the North Cascades are generally free of surface debris, when present the debris can insulate the ice and affect glacier response to climate variation.
Errors
For the 1958 coverage, the accuracy of paper maps was assumed to meet the USGS National Mapping Standards (http://rockyweb.cr.usgs.gov/nmpstds/nmas647.html), which require for horizontal position that 90% of 20 or more points surveyed in the field fall within 0.508 mm of the same identifiable points on the map. For the 1 : 24 000 maps used, 0.5 mm represents 12.2 m on the ground. We consider this uncertainty a minimum because in practice the Mapping Standards do not apply to mountainous topography (personal communication from J. Landwehr, 2000). The digitizing error, estimated from the width of the line denoting the glacier boundary on the 1 : 24 000 maps, is 2.4 m. The uncertainty in the 1958 glacier area was determined by calculating the area of a buffer around each glacier having a width equal to twice the root-mean-square error (6.2 m) of the mapping and digitizing errors. The uncertainty in glacier area for the 1998 coverage was estimated by comparing the area for individual glaciers to the areas independently measured from a digital orthophotographic quadrangle. Only the Cascade Pass Quadrangle, which included 13 glaciers, was available to us. The errors determined for each area were averaged over the 13 glaciers and used as an estimate for all the glaciers in the 1998 coverage.
Results
A total of 896 snow and ice features were found on the USGS maps for a total area of 128.1 ± 1.0 km2. Most (698) of these features were smaller than 0.1 km2. The smallest was 642 m2. In contrast, the Reference Post, Richardson, Tangborn and RosselotPost and others (1971) inventory counted 321 glaciers with a total area of 115.6km2. The primary reason for this difference is that Post and others deleted all mapped snow and ice features that did not fit their definition of a glacier, eliminating most features <0.1 km2. Filtering the 1958 USGS glacier inventory to the same 321 glaciers as Post and others (Fig. 1) resulted in a total ice-covered area of 117.3 ± 1.1 km2, 1.7 km2 larger than the Post and others inventory. The frequency distributions of glacier size of the filtered 1958 inventory and the Post and others inventory were very similar. The small differences between inventories can be attributed to map scale – Reference Post, Richardson, Tangborn and RosselotPost and others (1971) used a coarser scale, 1 : 38 000, compared to our 1 : 24 000 scale – and to the different technologies used to measure area. Post and others used mechanical planimeters to a precision of 0.1 km2, whereas we relied on the digital accuracy of the GIS (ArcView) with a precision of 0.001 km2. From this comparison we conclude that the 1958 USGS glacier inventory is equivalent to the manual inventory compiled by Reference Post, Richardson, Tangborn and RosselotPost and others (1971), and we use the filtered 1958 inventory as our base glacier coverage for comparison with more recent glacier coverage.
For the North Cascades Complex the average glacier area in 1958 was 0.37 km2 (standard deviation of 0.71 km2) with the smallest 0.01 ± 0.01km2 and the largest, 6.83 ± 0.19 km2. Glaciers ≤ 1.0 km2 accounted for 56% of the total glacier area and 93% of the glacier population (Fig. 2), whereas glaciers ≥ 5.0 km2 accounted for 10% of the glacier area and only 1% of the population. Average glacier elevation was 2011 m, with the lowest glacier at 1375 m and the highest at 2457 m. Glacier elevation increases to the east, away from the ocean, in agreement with Reference Post, Richardson, Tangborn and RosselotPost and others (1971). Average glacier slope is normally distributed about 34° and ranges from 12° to 62°, with the most frequent slope at about 20°. Most glaciers (71% of population, 65% of total area) were oriented north (between northwest and northeast). By 1998, the glacier population was 316 (loss of 5) and the total glacier area was 109.1 ± 1.1km2, a reduction of 8.2 ± 0.1km2 (7%) from 1958. Four of the five missing glaciers had areas <0.1 km2. Average glacier area for 1998 was 0.35 km2, with the largest glacier 6.53 ± 0.20 km2. As previously mentioned, slope, elevation and orientation for 1998 could not be calculated since 1998 topographic data were not available.

Fig. 2. Number of glaciers against area for 1958. Glaciers are grouped into 0.1 km2 intervals.
Glacier Volume
Glacier volume change is a key variable because it can be used to estimate mass change of the glacier and to estimate meltwater runoff. To estimate glacier volume, we used an area–volume scaling relation and tested several approaches (Reference Driedger and KennardDriedger and Kennard, 1986; Reference Chen, Ohmura, Lang and MusyChen and Ohmura, 1990; Reference Bahr, Meier and PeckhamBahr and others, 1997) to determine which was most suitable for our application. We compared the calculated results to five glaciers where volume change is known from repeated mappings of the glacier surface over time. Four of the glaciers (Silver, Noisy, North Klawatti, Sandalee) are within the park complex monitored by the National Park Service (J.L. Riedel and others, http://www.nps.gov/noca/massbalance.htm) and one glacier outside, South Cascade monitored by the USGS (Reference KrimmelKrimmel, 1999a). The ‘empirical’ volume difference was calculated by digitally superimposing DEMs with 10m horizontal spacing from 1992 to 1994 on that for 1958. The ‘theoretical’ volume change was found by subtracting the volumes predicted using area–volume scaling for glacier area at the time depicted. As expected, results show large errors in predicted volume change (Table 1). Because our sample size of five glaciers is small, our results are only suggestive. Reference Chen, Ohmura, Lang and MusyChen and Ohmura (1990) and Reference Driedger and KennardDriedger and Kennard (1986) consistently underestimate the volume change, while Reference Bahr, Meier and PeckhamBahr and others (1997) provide a more reasonable estimate. We therefore used the parameters of Reference Bahr, Meier and PeckhamBahr and others (1997) to estimate glacier volume change and used the average difference as the error. Although the error in the volume change for individual glaciers is large, our intent is not to use these values but to report instead the total ice volume change in the North Cascades Complex. Because the error is randomly distributed around the regression equation of the original area–volume relation (Bahr and others, 1997) the error on the aggregate should be smaller. Estimates of total ice volume in 1958 and in 1998 are 10.1 ± 0.2 km3 and 9.3 ± 0.2 km3, respectively. The difference represents a loss of about 0.8 ± 0.3 km3 (7.9%) or 6.7 ± 0.2 m surface lowering averaged over the 1958 glacier area. The average glacier thickness in 1958 was about 86 ± 0.2 m in 1958 and about 79 m in 1998.
Table 1. Volume errors (%) using the ‘empirical’ topographically derived volume change as the standard. The glacier names define the columns and AVG is the average error for the five glaciers

Analysis
To determine the influence of topographic characteristics, the fractional area change (FAC), the area change divided by the original 1958 area, was calculated and plotted against area, average elevation, orientation and slope. We also examined subgroups for glaciers <0.2 km2 in area and with elevations <1900 m (Table 2).
Table 2. Characteristics of glaciers grouped by fractional area change (FAC). C is class number; FAC is fractional area change since 1958. N, E, S and W are the number of glaciers oriented north, east, south and west, respectively
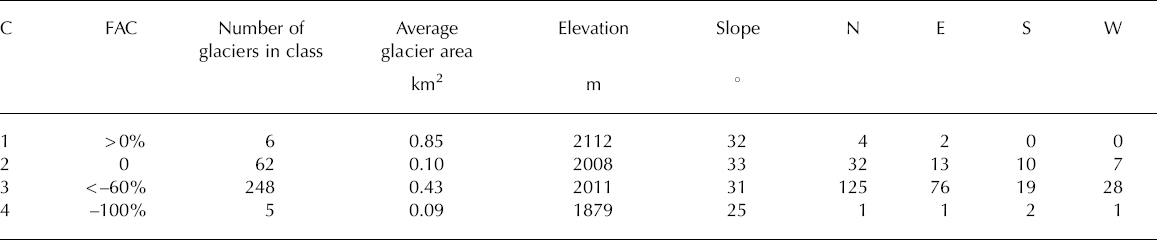
The FAC for individual glaciers ranged from +10.3% to –100%, with an average FAC of –11.4% and a median of –6.9% (Fig. 3). Six glaciers, 2% of the glacier population, have a positive FAC and are found at elevations higher than average. But not all glaciers at higher elevations increased in size, and nothing in the analysis points to a reason for enlargement. The increase may be due to error, as the FACs for these glaciers are well within the uncertainty (Fig. 3). Almost one-fifth, 19%, of the population showed no change, and the remaining 79% lost area, with five disappearing altogether. The average elevation of each class indicates that the higher the elevation the less the glacier shrinkage. However appealing this intuitive expectation, the elevation variability within each class overwhelms the difference between classes, indicating that local topographic effects presumably overwhelm the regional climatic trend within the region. We found no other consistent correlations with other topographic characteristics (aspect, slope, elevation). One clear trend is that smaller glaciers have greater FACs than larger glaciers (Fig. 3). According to the area–volume relation of Reference Bahr, Meier and PeckhamBahr and others (1997), it can be shown that smaller glaciers have a larger area-to-volume ratio than larger glaciers. Consequently, for the same ablation rate, smaller glaciers should shrink faster than larger ones.

Fig. 3. Individual glacier FAC against area. Open circles represent individual glaciers and the solid lines represent the error envelope about the axis.
Over the entire 40 year period, the volume of meltwater from net glacier mass loss in four watersheds in the park complex ranged from 0.1 to 7.4 x 106m3. This loss occurs mostly during August and September after much of the seasonal snow ablates, revealing glacier ice (Reference MeierMeier, 1969). Assuming all the net loss occurs in these 2 months, its contribution to average August–September runoff ranges from 0.1% to 6.0% (Reference GranshawGranshaw, 2002). This period is also the driest part of the year in this climate (Reference Jackson, Jackson and KimerlingJackson, 2003), and in terms of precipitation the net mass loss augments August–September rainfall by 1.0–15.7%.
Discussion and Conclusions
In 1958, the North Cascades National Park Complex had 321 glaciers having a combined area (volume) of 117.3 ± 1.1 km2 (10.1 ± 0.2 km3). By 1998 this population had decreased to 316, with the area dropping to 109.1 ± 1.1km2 (9.3 ± 0.2 km3). Between 1958 and 1998, combined glacier area decreased by 7% (8.2 ± 0.1 km2) and ice volume loss was 0.8± 0.1 km3.
These values equate to an average thickness loss of about 6.7 m of ice from all glaciers. Although a few glaciers enlarged over this time period, this change is well within the uncertainty. Five glaciers disappeared entirely and it is possible they were misclassified in the original Reference Post, Richardson, Tangborn and RosselotPost and others (1971) inventory. No correlations were found between magnitude of shrinkage and topographic characteristics of elevation, aspect or slope. A modest trend existed between average elevation and change class, whereby the glaciers that changed the least were at higher elevations. But the variation within class was much larger than between classes, indicating that local topography exerted a strong control compared to the weaker climatic trend with elevation. The only obvious relation was between glacier size and change. The fractional area change was greater for smaller glaciers.
The overall shrinkage in glacier area is less than that for specific glaciers elsewhere in the continental USA. For example, Reference Hall and FagreHall and Fagre (2003) show that Sperry and Grinnell Glaciers, in the Lewis Range of Montana ~ 500 km east of the North Cascades Complex, shrank by 30% in area over the same time period. South Cascade Glacier, within a few tens of kilometers of the complex, shrank by 22%. In contrast, Blue Glacier, about 120 km to the southwest of the complex, retreated by only about 34 m (2%) (Reference Conway, Rasmussen and MarshallConway and others, 1999). However, comparisons between individual glaciers and a sizable population of glaciers may be misleading.
A more apt comparison is made with the results from two European inventories, one in the Austrian Alps (Reference PaulPaul, 2002) consisting of 235 glaciers and one in Switzerland (Reference Kääb, Paul, Maisch, Hoelzle and HaeberliKääb and others, 2002; Reference Paul, Kääb, Maisch, Kellenberger and HaeberliPaul and others, 2004), which examined 938 glaciers. The distribution of glacier population with size is different between studies. The glacier population in the North Cascades Park Complex is shifted towards slightly smaller glaciers than in the Austrian population, and much smaller glaciers than the population in Switzerland, in which some glaciers exceed 100 km2 in area (in the North Cascades Park Complex they are all less than 10 km2). All regions show overall glacier shrinkage during the past three decades. The total loss in ice-covered area is greater for Switzerland (21%, 1973–98 (Reference Kääb, Paul, Maisch, Hoelzle and HaeberliKääb and others, 2002)) and Austria (18.3%, 1969–92 (Reference PaulPaul, 2002)) than the loss of only 7% in the North Cascades Park Complex from 1958 to 1998, despite our longer time interval. The reason for this difference in glacier shrinkage is unclear. All glacierized regions show glacier shrinkage, and greater fractional shrinkage with smaller glaciers. The North Cascades Park Complex is compared to the Swiss Glacier Inventory in Table 3 with similar results to that of the Austrian Alps (Reference PaulPaul, 2002) . We hypothesize, as previously mentioned, that smaller glaciers shrink faster than large glaciers under the same ablation regime because the area–volume ratio is greater for smaller glaciers.
Table 3. Comparison of glacier change by size class for the Swiss Glacier Inventory (SGI; Reference Paul, Kääb, Maisch, Kellenberger and HaeberliPaul and others, 2004) and the North Cascades National Park Complex (NOCA). The period for the SGI is 1973–98, while the period for NOCA is 1958–98

The large variation in the change of small glaciers is explained by Reference Kuhn, Warrick and BarrowKuhn (1993) who argued that some small glaciers may be quite stable against climatic variations because they reside in favorable topographic pockets on a slope fed by avalanches. Once the pocket is filled with snow, subsequent avalanches carry snow downslope. Because these glaciers have more snow available than they can physically trap, they are insensitive to variations in winter snowfall and their annual mass balance (and their area) is quite stable. By contrast, other glaciers are located in less favorable settings and are quite sensitive to climatic variations, resulting in large responses. We believe the observed difference in fractional area change (where smaller glaciers, on average, exhibit a much larger shrinkage than large glaciers) is due to the area–volume relation.
One important implication of this distribution of glacier change with size is that one has to be careful in identifying a ‘representative’ glacier for any given region. Indeed, many of our well-studied glaciers (e.g. South Cascade Glacier; Hintereisferner, Austria) are much larger than the average glacier size in the surrounding region and are probably not representative of area changes. Because glacier area and volume are linked, through scaling relations, studies that infer global glacier change from a small sample of monitored glaciers may under-represent the magnitude of glacier change and therefore its contribution to global sea-level change.
Acknowledgements
This research was made possible by the financial and technical support of the US National Park Service. Special thanks go to J. Riedel and R. Burrows (North Cascades National Park), R. Krimmel (USGS), A. Post and W. Tangborn (USGS, retired) and M. Pelto (North Cascades Glacier Climate Project, Nicols College). We also appreciate the efforts of two anonymous reviewers in improving the manuscript.








