Introduction
Renewed interest in snow fences for the protection of transportation facilities and other structures from snow-drifts has resulted from the success of the recently constructed snow-fence system along Interstate Highway 80 in south-eastern Wyoming (Tabler, [1973]).
If snow fences are to be successful, they must be designed with sufficient capacity to store the volume of snow transported over the course of a season as estimated by currently available methods (Reference TablerTabler, 1975; Reference Dyunin and KomarovKomarov, 1954 [a]). This requires that the maximum storage capacity of fences be known. Knowledge of the relationship between fence height and storage capacity is also required before economic analyses can be used to determine optimum barrier arrangements. Analysis of fence construction costs per unit volume of snow storage, for example, clearly demonstrates tall fences to be more economical than shorter ones (Reference TablerTabler, 1974).
The shape of drifts behind snow fences must also be known if fences are to be properly positioned. Maximum drift length determines the minimum distance a fence should be placed up-wind of the protected area, as well as proper spacing between multiple rows of fencing.
Detailed information on drift geometry is also essential to provide verification or calibration of wind-tunnel and water-flume simulations of snow-transport phenomena, as recently exemplified by Reference WuebbenWuebben (1978), and to provide a basis for a better understanding of the aerodynamics of snow fences, leading to improved design.
Numerous studies have been made of air flow behind artificial and natural barriers without snow-drifts, but unfortunately it is not yet possible to infer from this information the shape which a snow-drift will assume.
By comparison very few studies have been made of the drifts themselves. It is apparent from reviews by Reference SchneiderSchneider (1959) and Reference MellorMellor (1965) that no general consensus exists as to how drift characteristics are related to barrier geometry. One reason for the diversity of published results is the different experimental methods that have been used. Reference FinneyFinney (1934) and Nøkkentved (Reference PughPugh, 1950) used sawdust or mica to simulate drifts behind model barriers in wind tunnels. Although this classic work has provided many useful qualitative guidelines, it is likely that requirements for dynamic similarity were not met sufficiently to provide true geometric scaling of model and prototype.
Results of full-scale studies by Nøkkentved (Reference PughPugh, 1950), Komarov (1954[b]), Reference PricePrice (1961), and Croce (Reference MellorMellor, 1965) also provide conflicting results, probably because some investigators mistakenly identified immature drifts as having reached equilibrium. Other causes of disparate results include possible local terrain effects, and differences in weather conditions. Although there is no a priori reason why drift shapes should depend on wind speed over the relatively narrow range encountered naturally, many climatic and site factors affect the quantity of snow transport at a site, which in turn determines the likelihood of equilibrium conditions being attained.
Observations are required over many years and at numerous locations before maximum drift profiles can be known with any certainty. In addition, a wider range of heights should be studied than has been reported in the literature before the effect of height on drift geometry can be specified.
This paper presents results from extensive measurements of snow-drifts formed by horizontal-and vertical-slat snow fences having 50% porosity and heights from 0.8 to 3.8 m. These data, collected from 1962 to 1979 at more than 60 separate locations in south-east Wyoming, allow the most definitive assessment yet available of the geometry of drifts formed by snow fences.
Fence design, study sites, and measurements
Horizontal-slat fences
The horizontal-slat “Wyoming” fences were of the standard design used since 1971 by the Wyoming State Highway Department, as described by Reference TablerTabler (1974). These structures consist of horizontal boards 15 cm wide separated by 15 cm spaces, a bottom gap of approximately 0.1H (where H is vertical fence height), and a 15° inclination down-wind. Net porosity (open area) of the structure, excluding the bottom gap, is 48%, but averages about 50% over the total height.
The study fences are located along 70 km of Interstate Highway 80 between Laramie and Walcott, Wyoming, at elevations from 2 190 to 2 400 m. Of the 50 km of snow fence comprising the total system, 71% is 3.78 m in height, 6% is 3.17 m, 22% is 2.44 m, and 1% is 1.83 m in height. Lengths of the individual fences measured for this study range from 40 to 200 H.
The snow-drifting season typically extends from 1 November to 1 April, without appreciable melting. Average weather conditions during drifting, as measured at 2 m height over the 1971-72 winter and weighted according to mass flux, were as follows: 16 m/s wind speed at 260° azimuth, 80% relative humidity, –8°C air temperature, and 67.2 J/cm2 h incoming shortwave radiation (Tabler, unpublished).
Precipitation (water-equivalent) over the accumulation season averages about 250 mm, and the maximum recorded over the period of study (1971 to 1979) was 350 mm.
Measurements presented here are restricted to sites on gently sloping (<5%), uniform terrain. Contributing distance, or “fetch”, extends 2-6 km up-wind of the study fences. Vegetation consists of low-growing (<30 cm) shrubs and grasses. The seasonal snow transport coefficient defined by Komarov (1954[a]) ranges from about 0.5 to 0.75, which compares to the same author’s value of 0.7 for Siberia.
Vertical-slat fences
Vertical-slat fences were of the typical wood lath and twisted wire construction, referred to by Pugh (1950, p. 4) as “Canadian” fencing. Typical dimensions included slats 3.8 cm wide, spaced at 5.5 cm, resulting in a porosity of about 59%. These fences were installed vertically, with a 15 cm bottom gap. Fence heights of 0.8, 1.37, 1.83, 2.44, 3.05, 3.66, and 4.88 m were studied, but equilibrium drifts were only observed for the 0.8, 1.37, and 3.05 m heights.
The 0.8 m fences were installed at two of the sites described for the horizontal-slat fence studies. The single 3.0 m fence to attain equilibrium was part of a water yield-improvement project at lat. 41° 59’ N., long. 105° 30’ W., elevation 2235 m. All other vertical-slat fences were installed within a 3 km radius of lat. 41° 16’ N., long, 105° 22’ W., at elevations between 2 370 and 2 530 m.
Winter precipitation (water-equivalent) averages about 150 mm, with occasional years as high as 250 mm. Mean 2 m wind speed during drifting was 12 m/s, measured over the 1970—71 winter, with other weather and site conditions similar to those described for the horizontal-slat fences (Reference TablerTabler and Schmidt, 1973).
Measurements
Snow depths were measured directly with an aluminum probe at 3 m intervals along transects parallel with the prevailing wind. Snow profiles were also measured normal to fences used for a study to determine effect of wind orientation. All other fences were oriented within 15° of perpendicular to the wind. Snow densities were also sampled at 3 m intervals, using a standard Federal (Mount Rose) snow tube. In most years, only three to six such transects were needed to characterize snow density adequately.
Transects were located no closer than 15H from the ends of the fences to avoid the curved part of the drift caused by wind sweeping around fence ends (Reference TablerTabler, 1974). The number of transects measured at each fence varied from one to three, depending on the uniformity of the drift and the underlying ground surface.
For horizontal-slat fences, measurements were repeated annually from 1971 to 1979 at the same locations at each fence where possible. Measurements at vertical-slat fences could only be repeated over two to three years before the fences were moved to new locations whose positions were dictated by the objectives of other studies.
Although in some years measurements were repeated after each significant drifting event throughout the winter, measurements usually began with the arrival of above-freezing temperatures in February or March and were repeated after subsequent drifting events until it was certain that maximum accumulation had been reached for the season. These repetitious measurements allowed equilibrium conditions to be identified when snow accumulation did not increase over one or more major drifting periods.
The number of fences measured varied from year to year, depending on time available for measurements and objectives of other studies in progress.
During the years when the vertical-slat fences were studied (1962 to 1970) we did not regard the up-wind drift as a significant feature, and so failed to take sufficient measurements to characterize the up-wind drifts at equilibrium.
Drift geometry (longitudinal)
Equilibrium drifts
It is reasonable to assume that any given snow fence has a maximum snow-retention capacity which cannot be exceeded regardless of the quantity of blowing snow arriving at the fence. The snow-drift formed by a fence that has reached this ultimate condition is said to be at “saturation” or “equilibrium”. The latter term is used in this paper to avoid possible confusion with free-water content of the drift.
If development of a snow-drift follows the so-called law of natural growth, so that at any given time growth rate is inversely proportional to total accumulation up to that time, then trapping efficiency of the fence might be expected to decline in some manner as the fence fills with snow. If so, the true “equilibrium” profile may be approached as a limit, but may not be attained with a finite amount of snow transport.
Although there is no way to be certain that true equilibrium has indeed been attained for any particular fence in the field, the primary criterion used for this study was cessation of drift growth before the drifting season ended. Where possible, values thus assumed to represent equilibrium conditions were further substantiated when essentially identical profiles were measured behind the same fence over two or more years having different quantities of snow transport.
During the 18 years of study summarized in this paper, equilibrium drifts were measured at 18 horizontal-slat fences, and 14 vertical-slat fences. Dimensions for these drifts are presented in Table I, and empirical relationships derived from the data are summarized in Table II. For comparison, results published by other investigators are given in Table III.
If drifts are geometrically scaled with fence height H, then all drift dimensions must be proportional to H, so that
where y is drift depth at distance x from the fence. Drift length L, maximum depth ymax, and cross-sectional area A would therefore be given by
The equilibrium profiles plotted in Figures 1 and 2 indicate the requirement of Equation (1) is met, and the regressions in Table II imply that (2a), (2b), and (2c) are valid. The equilibrium drifts may therefore be considered geometrically scaled over the range of heights for which data are available.
A polynomial regression curve (Fig. 1) for the horizontal-slat fence lee drift, using data from the 2.44, 3.17, and 3.78 m heights, is

This was the lowest degree of polynomial that provided a reasonable fit to the data.
The curve (Fig. 2) approximating the profile of the lee drift for the verlical-slat fences is

Only data for the 1.37 m height were used in determining regression equation (3b). This was because depth measurements behind the 0.76 m fence were subject to substantial errors (Figure. 1 and 2) because irregularities of the underlying ground were significant relative to the height of the fence. Also, the 3.05 m fence was nearly buried due to several drifting events having winds of opposite direction from the prevailing winds, thus making the drift shape near the fence atypical.

Fig. 1. Profiles of equilibrium drifts formed by horizontal-slat, 50% porous snow fences on level terrain.

Fig. 2. Profiles of equilibrium lee drifts formed by vertical-slat, 60% porous snow fences on level terrain.
Reference PricePrice (1961) suggested (based on the observation of Reference ChorleyChorley (1959) that a lemniscate equation can be used to describe streamlined forms) that the shape of snow-drifts could be mathematically represented by the “rose” equation (in polar coordinates)
where r is the vector distance from the down-wind end of the drift, L and l are distances from the fence to the leeward and windward ends of the drift, respectively, and η is given by

where A is cross-sectional area of the drift. Reference TablerTabler (1974) has shown that the lemniscate equation
where
provided a better fit to lee drifts formed by horizontal-slat fences. Neither Equations (4) nor (5) adequately represent shapes of the equilibrium drifts shown in Figures 1 and 2, but the empirical polynomial Equations (3) provide adequate approximations.
From Figures 1 and 2 and Table I, maximum lee-drift depth is seen to be about 1.20H at 6.7H distance for horizontal-slat, and 1.06H at 5.7H distance for vertical-slat fences. This difference may be due to the 15° leeward inclination of the Wyoming design. Drift length is 29.5H for the horizontal-slat and 26.5H for the vertical-slat fence.
Table I. Mean measured dimensions for equilibrium drifts (with 95% confidence intervals)

Average tail slope of the drifts, as measured between down-wind distances of 12H and 22 H, is about 6% for both types of fence (Table II). This slope is the same as that of the halfangle generally recognized as the threshold for separation of flow through two-dimensional divergent channels (diffusers) (Reference ChangChang, 1970), and apparently reflects the pressure gradient required to maintain a uniform longitudinal distribution of surface shear stress.
Cross-sectional area is shown as a function of fence height in Figure 3, which also shows measurements of four “Swedish” fences of the design described by Pugh (1950, p. 5). Areas of lee drifts are approximated by Horizontal-slat fences :
Vertical-slat fences:
Drifts on the up-wind side of horizontal-slat fences had a maximum depth of about 0.5H, and a length of 12H. Cross-sectional area is approximately
Although the results presented here suggest larger dimensions than previously reported by most investigators (Table III), there is notable agreement with the single example for a 2 m fence given by Komarov (1954[b]) and Reference Dyunin and KomarovDyunin and Komarov (1954).
Table II. Summary of empirical expressions describing dimensions of equilibrium drifts
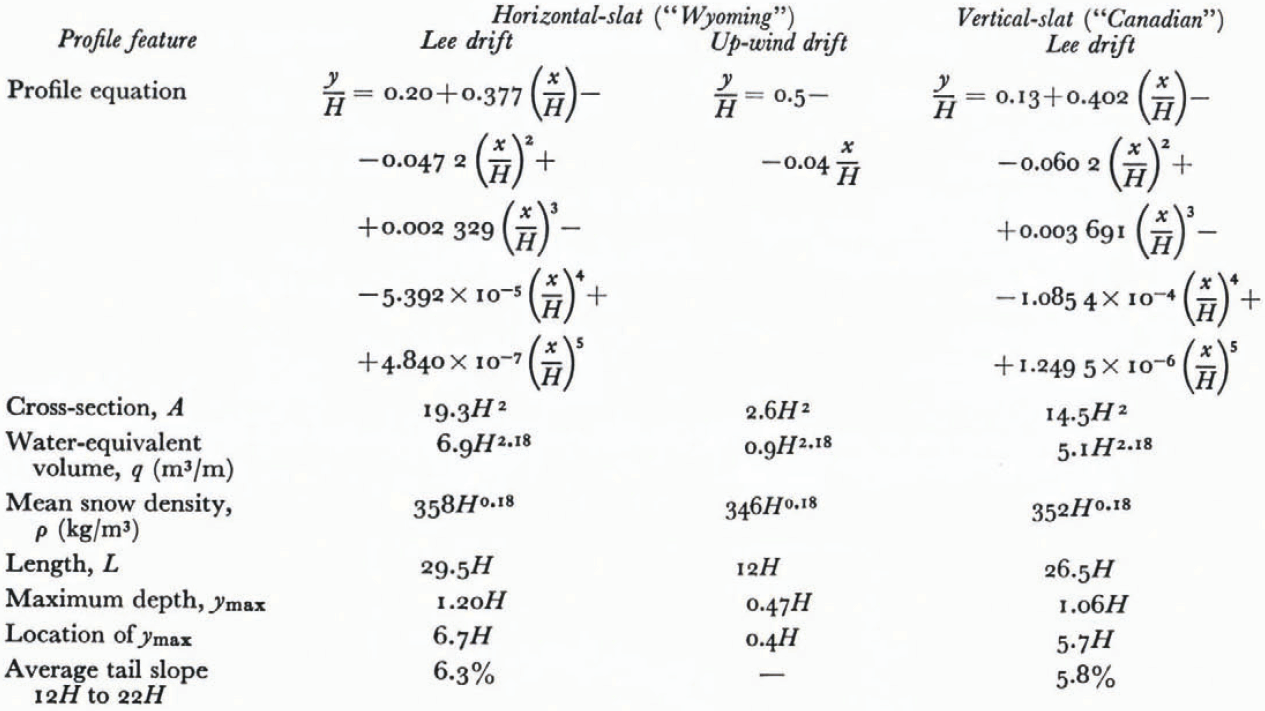

Fig. 3. Cross-sectional area of equilibrium drifts as a function of fence height,for data in Table I
Pre-equilibrium drifts
In this section, dimensions of drifts before equilibrium is attained are expressed as functions of “relative drift area” S defined as the ratio of cross-sectional area of a drift to that expected at equilibrium. Pre-equilibrium geometry will only be analyzed for the horizontal-slat fences which provide a better range of heights and more definitive equilibrium values. Polynomial regression equations have been fitted to the pre-equilibrium data for those relationships where they provide reasonable approximations to trends. These empirical equations are not valid beyond the range of data shown in the figures.
Table III. Summary of lee-drift dimensions reported in literature for 50%
porous fences with height H


Fig. 4. Maximum depth of lee drifts formed by horizontal-slat fences as a function of cross-sectional area relative to that at equilibrium.
Maximum depth, location of maximum depth, and length of the lee drift are shown as functions of relative drift area in Figures 4 to 6. These presentations provide estimates of critical drift dimensions prior to equilibrium, and provide insight into how drifts grow. When a 3.8 m fence half-filled to capacity (S = 0.5), for example, maximum depth of the lee drift would be approximately 1.05H at is about 6.5H from the fence, and total drift length would be about 16H. Estimates for drift length prior to saturation are essential when it is necessary to place a tall fence, which is not expected to fill, as close to the protected area as possible.
The relatively slow growth in drift length up to S = 0.5 in Figure 6, coincides with the period of time the steep “slip face”, or cornice, dominates the geometry. It is possible that relationships such as those shown in Figures 4 to 6 can be used to deduce changes in trapping efficiency.
Growth of the up-wind drift relative to that of the lee drift is shown in Figure 7. This relationship suggests that up-wind drift area is about 13% of that of the lee drift throughout the pre-equilibrium period. There is also some indication that the area of the windward (Figure.5 and 6) drift attains a maximum value of about 3H 2, even though the lee drift may continue to grow due to a terrain depression or an interaction with another row of fencing down-wind.

Fig. 5. Location of maximum depth of lee drifts formed by horizontal-slat fences as a function of cross-sectional area relative to that at equilibrium.

Fig. 6. Length of lee drift formed by horizontal-slat fences as a function of cross-sectional area relative to that at equilibrium.
Maximum depth of the up-wind drift with respect to that of the lee drift, is shown in Figure 8. This relationship suggests that maximum depth of the up-wind drift increases rapidly once the lee drift depth exceeds the height of the fence.
Geometry near fence ends
criteria for overlapping staggered fences, extension required beyond the protected area, and minimum length must be developed from a knowledge of how capacity of a snow fence varies as a function of distance from the end of the fence. For a fence oriented exactly normal to the wind, ends of the lee drift are rounded by wind sweeping around the fence. This effect (Figure.7 and 8) is due to turbulence generated at the fence boundary, an acceleration of air flow around the ends of the fence, and the response of air flow to lateral pressure gradients developed behind the barrier.

Fig. 7. Cross-sectional area of up-wind drift AuP as a function of lee drift area Alee, for horizontal-slat fences. Areas are made dimensionless by dividing by the square of fence height H2.

Fig. 8. Maximum depth of up-wind drift as a function of lee-drift depth for horizontal-slat fences.
Data for 6 horizontal-slat fences show this end-effect on cross-sectional area to extend inward as far as 12H from the end of the fence (Fig. 9). Drift length varies with distance from the fence end as shown in Figure 10.
Effect of wind orientation
The effect of fence orientation (i.e. wind attack angle) on drift geometry is important in determining to what degree fences can be skewed with respect to prevailing wind direction.

Fig. 9. Relative cross-sectional area of lee drift as a function of distance from end of horizontal-slat fences.

Fig. 10. Relative length of lee drift as a function of distance from end of horizontal-slat fences.
The limited data shown in Figure 11 suggest that cross-sectional area of a lee drift, as measured perpendicular to the fence, varies directly as the cosine of the wind departure angle. This implies that geometry of a lee drift, as measured parallel to the wind, is independent of fence orientation up to departure angles of at least 75°. This generalization only applies to very long fences (the fences used for these measurements had lengths of 50H to 200H), and does not necessarily imply that trapping efficiency is unaffected by wind orientation.
Density of snow-drifts
The mean vertical snow densities shown in Figure 12, represent only those measurements taken during the accumulation season, before the beginning of melt. At the locations used in this study, melt is usually negligible over the drifting season, so that densification is due (Figure.11 and 12) primarily to compressive loading by the overlying snow. As a result, the depth-density relationship is relatively consistent from year to year.

Fig. 11. Relative area of lee drift as a function of wind-departure angle. Drift area parallel to wind Aw was measured behind fences oriented perpendicular to the prevailing wind.

Fig. 12. Average (vertical) snow density as a function of snow depth for drifts before melt. Density was measured with a Federal sampler and corrected for overestimation.
Because it is generally recognized that the Federal (Mount Rose) snow sampler tends to overestimate density, the measured values were corrected using a modification of the empirical equation developed by Reference Peterson and BrownPeterson and Brown (1975):
where ρm is measured snow density (in kg/m3), and ρc is the corrected density. The correction is thus 2% at 300 kg/m3 and 10% at 500 kg/m3.
An average curve fitted to all years of data for snow depths y is
In general, densities predicted by Equation (9) for depths to 5 m are within 10% of published values for polar and alpine snow, as summarized by Reference KeelerKeeler (1969). Although validity of this regression equation is strictly limited to the range of depths used for its development, values predicted for depths between 20 and 100 m are also within 10% of those reported for deep cores from interior Greenland (Langway, cited by Reference BensonBenson (1962); Miller, unpublished). Equation (9) closely coincides with values expected for the lower limit of the “soaked” glacier facies, as typified by Greenland Station 0-35 (Reference BensonBenson, 1962).
Storage capacities of snow fences must be expressed in terms of water-equivalent if they are to be comparable with mass transport estimates used for designing snow-fence systems. Snow-drift water-equivalent volume q, expressed in m3 per meter of fence length, is given by

where ρw is the density of watery is snow depth, and x is distance from the fence. Numerical integration of Equation (10) for fence heights to 5 m, after substituting expressions for ρc (Equation (9)) andy,from the profile Equations (3), give the approximations horizontal-slat fences:
vertical-slat fences:
where q lee is water-equivalent volume of the lee drift (in m3/m), and H is in meters.
A similarly derived approximation for water-equivalent volume of the drift on the up-wind side of horizontal-slat fences is
The mean snow density for drifts is given by

Substituting Equations (6) and (11) into (13), mean snow density for lee drifts can be approximated by horizontal-slat fences:
vertical-slab fences:
Discussions and conclusions
Results reported here are restricted to snow fences having 50% porosity located on nearly level surfaces, and future studies will be needed to develop methods for predicting drift geometry in irregular terrain.
As a general rule over the commonly used range of fence heights, lee-drift geometry is characterized by length proportional to fence height H and cross-sectional area proportional to H 2. Water-equivalent volume, however, is approximately proportional to H 2.18 due to the increase in densification with snow depth. This suggests an even greater economic advantage of tall fences than was indicated from an analysis based on cross-sectional area (Reference TablerTabler, 1974).
These results imply that equilibrium drifts are geometrically scaled with height over the range 0.8 to 4 m. In another paper (Reference TablerTabler, 1980), the author has shown from outdoor modeling studies on lake ice that the relationship extends to heights as low as 0.06 m, and hypothesizes that dynamic similarity requirements are satisfied over a period of time because surface roughness height z0 varies approximately as the square of shear velocity u⋆ in saltating flows in air.
The relatively limited data for vertical-slat fences do not allow as much confidence to be placed in the results for this design. In comparison with the Wyoming horizontal-slat fences, however, it appears that drifts behind vertical-slat Canadian fences tend to be about 10% shorter and 12% shallower, resulting in 26% less water-equivalent volume. It is uncertain how much of this difference is due to the 15° inclination of the Wyoming design as compared to differences in porosity and dimensions and orientation of the slats.
As mentioned previously, there is no way to be certain that the drifts considered to be at equilibrium are actually the maximum drifts possible for the fence designs studied here. The author noted in an earlier paper (Reference TablerTabler, 1974) that drifts behind the Wyoming fence appeared to have a cross-sectional area of 18H 2 and a length of 24H, based on two years of measurements. A comparison with the new estimates after eight years of study demonstrates that, although future observations may also lead to upward revisions of maximum dimensions, it seems unlikely that ultimate estimates would depart significantly from those presented here.
Acknowledgements
Research reported here was supported in part by the Wyoming State Highway Department. The author gratefully acknowledges the invaluable assistance of research technician Robert L. Jairell in the collection of data over the last 16 years of this study.

















