1. Introduction
With the increase in computing power in recent years, solving inverse problems has become feasible. In a forward problem, the values of the model parameters are known, and observable quantities are calculated based on those known parameters. For the corresponding inverse problem, the goal is to determine the values of the model parameters, based on observed data. Many inverse problems in glaciology can be formulated and reliably solved. An example of an inverse problem is the estimation of basal sliding from measurements of the ice-surface velocity and the geometry of a flowband (e.g. Reference TrufferTruffer, 2004). Formulating a formal inverse problem makes it possible to deduce information about parameters that are not otherwise easily measured. Solving an inverse problem requires a well-defined forward problem, which consists of an algorithm that calculates observable quantities from specific model parameters. An inverse problem can be formulated in different ways. Formulating an inverse problem is an important step, since it is at this stage that any a priori information about the solution, or constraints on the solution, can be introduced into the problem. Once the inverse problem has been formulated and a forward algorithm has been developed, a variety of tools are available to solve the formulated inverse problem. Each tool has advantages and disadvantages, and the most appropriate tool must be chosen carefully, according to the specific problem. Whenever possible, it is important to use several tools to solve an inverse problem, since multiple approaches may reveal more information about the solution.
Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) formulated a steady-state inverse problem to recover spatial patterns of accumulation using deep internal layers, ice-sheet surface and bed topography, and other available data. As part of this inverse problem, the associated forward algorithm generates an internal layer in a flowband based on model parameters of accumulation rate, layer age, and the influx of ice at the upstream end of the flowband. Internal layers, which are interpreted as horizons of constant age, can be detected using ice-penetrating radars (e.g. Reference Paren and RobinParen and Robin, 1975). The inverse problem formulated by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) seeks model parameters that generate an internal layer that fits the available data at an objective tolerance criterion. Their formulation finds a spatially smooth accumulation-rate solution. The forward algorithm of Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) tracks particles along a steady-state flowband of non-uniform width by integrating the velocity field. The positions of particles of equal age map out a calculated internal layer. In this inverse problem, following Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007), we define a layer to be deep when its depth cannot be reproduced from local accumulation and strain rates; the entire particle trajectories must be considered.
Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) solved the inverse problem using the Gradient method (e.g. Reference TarantolaTarantola, 2005). The Gradient method performs a local search for the maximum-likelihood solution for the model parameters. This method can find only a single solution, unless a range of initial guesses are made. The solution found using the Gradient method could be a secondary solution if several solutions are present. This drawback can prevent the search from revealing the best model that could generate the observed data (Reference Mosegaard and TarantolaMosegaard and Tarantola, 1995). Since the Gradient-method solution consists of only one set of model parameters, information about the correct solution could be lost. The advantage of this method is that it requires relatively little computation and therefore can run relatively fast. In contrast to the Gradient method, the Monte Carlo (MC) method does a global search, sampling models from the entire solution space in correspondence to our a priori information about the solution and the data and their uncertainties. This method has the ability to discover whether multiple solutions fit the data. Based on statistics, it can provide the mean and standard deviation of the solution(s). The disadvantage of this method is that it requires more computation time.
In this paper, we weigh the advantages and disadvantages of the MC and Gradient methods. After describing the general principles involved we illustrate these concepts using a particular dataset from Taylor Mouth, a flank site off Taylor Dome, Antarctica (Fig. 1). For consistency, the same forward algorithm and the same observed data parameters have been used in both methods. This study will determine whether the solution recovered using the Gradient method is representative of the most likely solution, or whether it represents only a secondary solution caused by the search algorithm getting trapped in a secondary well. We present results from different formulations of the inverse problem, showing how different constraints and preconception values affect the solution of the inverse problem. This thorough analysis of different formulations will help when addressing future inverse problems, as it shows the advantages and weaknesses of the different formulations. It is not always possible to use several formulations when solving an inverse problem because the problem considered may be too computationally expensive. Our analysis can provide guidance on which formulation to use when solving an inverse problem relating internal layers to accumulation-rate patterns, as well as other inverse problems.

Fig. 1. Inset shows location of study area, Taylor Mouth, in Antarctica. Black solid curve represents our flowline. Taylor Dome ice core is marked by a solid dot. Taylor Mouth core site is shown with an open dot.
2. The Taylor Mouth Problem
The Taylor Mouth problem described by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) belongs to a group of problems in glaciology in which information about the accumulation rate and age of the internal layers is sought, based on internal layers in glaciers or ice sheets. As more radar profiles are obtained every year from Greenland and Antarctica, as well as smaller ice caps around the Arctic, it is desirable to define strategies for obtaining information from these data. In order to present possible different strategies for solving the inverse problem to determine the age of an internal layer and the accumulation-rate profile, we solve the problem using data from Taylor Mouth, and compare our solution to that of Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007). We use the surface, bed and flowband-width geometry of Taylor Mouth and an estimate of the age of the tracked internal layer (shown in Fig. 2 as a dashed curve), the influx into the upstream end of the flowband, and the accumulation-rate profile along the flowband. Based on these parameters, the forward algorithm returns the depth of the layer and the surface velocity along the flowband. Using the shallow-ice approximation (e.g. Reference PatersonPaterson, 1994, p.262) and ice deformation, defined by a temperature-dependent Glen-type flow law (e.g. Reference PatersonPaterson, 1994, p.85), the forward algorithm tracks particles by integrating the velocity field. This is based on the expectation that surface-parallel shear strain rate dominates the ice flow and that temperature controls its magnitude. Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) give a detailed description of the forward algorithm. The particles are tracked through both space and time along a steady-state flowband with non-uniform width. The forward algorithm calculates the ice velocity, ice-temperature field, ice-surface topography and shapes of internal layers. Points of equal age on all the paths form an internal layer.

Fig. 2. Ice-penetrating radar profile along our flowband at Taylor Mouth (2 MHz center frequency) (Reference GadesGades, 1998). The Taylor Mouth 100 m core at 11.4 km is indicated by a vertical bar. The internal layer used in this inverse problem is marked by a dashed curve.
3. Model and Data Distributions and Their Respective Spaces
The model space,
![]() , is spanned by the set of model parameters, each of which constitutes a dimension in the model space. A set of values for the model parameters represents a specific point in the model space. Such a point constitutes a model in the model space and is denoted by a vector, m. The data space is defined in a similar way, with each data parameter representing a dimension and an observed dataset representing a point denoted by a vector, d, in the data space,
, is spanned by the set of model parameters, each of which constitutes a dimension in the model space. A set of values for the model parameters represents a specific point in the model space. Such a point constitutes a model in the model space and is denoted by a vector, m. The data space is defined in a similar way, with each data parameter representing a dimension and an observed dataset representing a point denoted by a vector, d, in the data space,
![]() . When solving an inverse problem the goal is to estimate those values of the model parameters which, when mapping them using a forward algorithm from the model space to the data space, recreate the observed data with regard to their uncertainties.
. When solving an inverse problem the goal is to estimate those values of the model parameters which, when mapping them using a forward algorithm from the model space to the data space, recreate the observed data with regard to their uncertainties.
Here we define some important terms regarding probability distributions that we use to describe the data and model parameters. Table 1 summarizes these probability distributions. One of the main problems when visualizing the probability distributions for the data and model parameters is the high dimensionality of the spaces. To introduce the concepts, we visualize two parameters spanning a two-dimensional space, m and d, where m is mapped over into d; adding additional parameters is equivalent to adding extra dimensions. An example of a probability distribution, ρ(m, d), for sets of values of the two parameters, m and d, is shown in Figure 3a. Sets of parameters from darker areas are more likely than sets of parameters from lighter areas.
Table 1. The different probability distributions introduced in the text


Fig. 3. (a) An example of a probability distribution for parameters m and d. Darker areas indicate sets of m and d that are more likely. (b) A non-exact mapping of parameter m into parameter d. If the mapping had been exact, this would be a solid curve rather than a gray shaded area. (c) Joint probability distribution between the probability distribution shown in (a) and the information relating parameters m and d shown in (b). (d) Marginal probability distribution of the joint probability distribution for parameter m.
Another probability distribution is shown in Figure 3b. This distribution, represented by Θ(m, d), is a mapping of the parameter space of m into the parameter space of d. However, this mapping might not be exact; a given m may be mapped into a range of possible values of d. An example of such a mapping could be a forward algorithm with some built-in noise or uncertainty.
We can combine the two probability distributions shown in Figure 3a and b to obtain more information about how parameters m and d relate to each other. The result is called the joint probability distribution, σ(m, d); it is defined as the product of the two original probability distributions. An example of a joint probability distribution between the distributions shown in Figure 3a and b is shown in Figure 3c.
Once the joint probability distribution is defined for a set of parameters, we can find the probability distribution for a single parameter, or a subset of parameters. This distribution is called the marginal probability distribution, denoted by σ mar(m). An example of the marginal probability distribution for parameter m is shown in Figure 3d. The marginal probability distribution is calculated by integrating the joint probability distribution over all the parameters other than the one parameter (or set of parameters) for which the marginal probability distribution is sought.
We use the terms ‘a priori’ and ‘a posteriori’ probability distributions. These refer, respectively, to the probability distribution before introducing information about any available data and to the probability distribution after we have incorporated information about data, a priori knowledge and relations that map model parameters into the data space. Hereafter, parameters m and d are vectors, spanning the model and data space where each parameter constitutes a dimension.
The measured data for this problem constitute only a single point, d
obs, in the data space, but since there is an uncertainty associated with every measurement, the real values of the observable quantities may differ from the data, d
obs. The observable quantities are therefore represented by a distribution in the data space centered around their measured values, rather than by a single point in the data space. This distribution we call the probability distribution of observable quantities,
![]() . The probability distribution is a normal distribution when it is assumed that the measurement errors are normally distributed. In the same way, for our a priori knowledge about the values of the model parameters, we expect the model parameter values to be given by a probability distribution centered around our best guess, their preconception values. The characteristic widths of their probability distributions are given by our confidence in their preconception values. This distribution, which we call the probability distribution of the model parameters,
. The probability distribution is a normal distribution when it is assumed that the measurement errors are normally distributed. In the same way, for our a priori knowledge about the values of the model parameters, we expect the model parameter values to be given by a probability distribution centered around our best guess, their preconception values. The characteristic widths of their probability distributions are given by our confidence in their preconception values. This distribution, which we call the probability distribution of the model parameters,
![]() , is situated in the model space. All available information about the data, the model parameters, the forward algorithm, the data space and the model space is used to create the a posteriori probability distribution of the model parameters, σ(d, m). The solution to the inverse problem can then be inferred from this distribution.
, is situated in the model space. All available information about the data, the model parameters, the forward algorithm, the data space and the model space is used to create the a posteriori probability distribution of the model parameters, σ(d, m). The solution to the inverse problem can then be inferred from this distribution.
The probability distribution, σ(d, m), representing the a posteriori information, is the joint probability between the probability distribution for the model parameters,
![]() , and the probability distribution for the data,
, and the probability distribution for the data,
![]() , along with the distribution, Θ(d, m), of the calculated observable quantities produced by mapping a model into the data space (Reference TarantolaTarantola, 2005); Θ(d, m) is also called the theoretical probability distribution of calculated observable quantities. Therefore, the a posteriori probability distribution is expressed as
, along with the distribution, Θ(d, m), of the calculated observable quantities produced by mapping a model into the data space (Reference TarantolaTarantola, 2005); Θ(d, m) is also called the theoretical probability distribution of calculated observable quantities. Therefore, the a posteriori probability distribution is expressed as
The distribution σ(d, m) is normalized by a constant, k, such that it integrates to unity. To correct for any nonlinear features of the joint data and model space, a distribution μ(d, m) is introduced into the equation for the a posteriori probability. This could, for example, be necessary if a spherical coordinate system, which is not a linear space, was used for the model or data space. This distribution, μ(d, m), is called the homogeneous probability density for the joint data and model space (Reference Mosegaard, Tarantola, Lee, Kanamori, Jennings and KisslingerMosegaard and Tarantola, 2002). For the combined data and model space in the Taylor Mouth example, μ(d, m) is unity. Formally, the a posteriori probability distribution for the model and data parameters is not the joint probability between the different distributions. This is because the probability distribution for the model parameters is not independent of the probability distribution for the data when the probability distribution for the model parameters is affected by the data. We will assume here that the error introduced by assuming independence is negligible. The a posteriori probability distribution of models in the model space is the marginal probability distribution over the data space, defined as the integral over the data space of the a posteriori probability distribution. This is written as
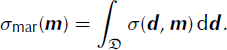
This allows the a posteriori probability distribution of the models to be written as the product between the probability distribution of the model parameters and a likelihood function, L(m), that indicates how well the model, m, explains the data (Reference TarantolaTarantola, 2005):
with the likelihood function given by
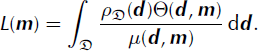
Assuming that the theory for calculating the observable quantities based on a model is exact, i.e. the uncertainties in the calculated observable quantities are negligible compared to the uncertainties in the data, the calculated observable quantities from the mapping of a model m into the data space can then be represented by a Dirac delta function. The theoretical probability distribution of calculated observable quantities is then
![]() , where d
cal = f(m) are the calculated observable quantities based on a model, m, using a forward algorithm, and
, where d
cal = f(m) are the calculated observable quantities based on a model, m, using a forward algorithm, and
![]() is the homogeneous probability density for the model space. According to the definition of Reference Mosegaard, Tarantola, Lee, Kanamori, Jennings and KisslingerMosegaard and Tarantola (2002), this forward problem is only weakly nonlinear and, since the data space is seen to be a linear space, the likelihood function is reduced to the probability distribution for the calculated observable quantities,
is the homogeneous probability density for the model space. According to the definition of Reference Mosegaard, Tarantola, Lee, Kanamori, Jennings and KisslingerMosegaard and Tarantola (2002), this forward problem is only weakly nonlinear and, since the data space is seen to be a linear space, the likelihood function is reduced to the probability distribution for the calculated observable quantities,
![]() .
.
The probability distribution of the model parameters can be formulated in different ways depending on the goal of the investigation. Three different formulations are compared here which we call ‘smallest’, ‘flattest’ and ‘smoothest’. In a ‘smallest’ formulation, the value of the probability distribution is defined by the distance between the model parameters and their respective preconception values. If the model parameters are assumed to have a geometrical relationship, other formulations are also possible. In a ‘flattest’ formulation, the value of the probability distribution is defined by the deviation of the slope of the model-parameter profile from a slope of zero. In a ‘smoothest’ formulation, the probability distribution is defined by the deviation of the curvature of the model-parameter profile from zero curvature. Using a ‘flattest’ or ‘smoothest’ formulation is possible only if the model parameters have a spatial or temporal relationship to one another. The problem described by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) can be formulated using either a mixed ‘smallest’ and ‘smoothest’ probability distribution or a pure ‘smallest’ probability distribution.
4. Inverse-Problem Formulation
The solution to the inverse problem is highly dependent on its formulation, because this is how any a priori information and constraints on the solution are included. Three different formulations of the inverse problem are presented here in order to explore their similarities and differences. The different formulations are characterized by the way in which the likelihood function and the probability distribution for the model parameters are defined. The three formulations are Tikhonov regularization and Occam’s inversion, both of which use a mixed ‘smallest’ and ‘smoothest’ formulation of the probability distribution, and Bayesian inference which uses a pure ‘smallest’ formulation.
4.1. Tikhonov regularization
One of the goals of this investigation is to determine how well a MC method performs compared to a Gradient method. To obtain a stable and physically reasonable solution with the Gradient method, the inverse problem can be regularized using Tikhonov regularization. Since the solution obtained from the MC simulation should be comparable to the solution obtained from the Gradient method, the Tikhonov regularization is defined similarly to the definition given by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007). The idea behind the Tikhonov regularization is that the solution should neither overfit nor underfit the data. This constraint is important because the observed data contain measurement errors, and because the theory (i.e. the forward algorithm) coupling the model parameters and the observed data may be imperfect. This means that the solution to the inverse problem will contain only structure that is required by the observations, within their measurement uncertainties. (For a more detailed description of Tikhonov regularization see, e.g., Reference ParkerParker, 1994; Reference Aster, Borchers and ThurburAster and others, 2005, ch. 5.) To regularize our inverse problem, the misfit criterion, which will be met by adjusting the weight on the observed data, is defined as
where ||d|| is referred to as the data norm given by

where
![]() is the ith calculated observable,
is the ith calculated observable,
![]() is the ith observed data parameter and
is the ith observed data parameter and
![]() is the standard deviation of the ith observed data parameter. N
d is the number of data parameters. An estimate of the tolerance, T, is given by Reference ParkerParker (1994, p.124) as
is the standard deviation of the ith observed data parameter. N
d is the number of data parameters. An estimate of the tolerance, T, is given by Reference ParkerParker (1994, p.124) as
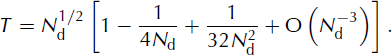
The age of the layer, and the flux into one end of the flowband are denoted, respectively, by ‘age’ and ‘Q in’. The probability distribution for these two model parameters is defined as
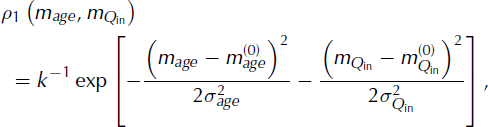
where superscript ‘(0)’ on the model parameters indicates the preconception value. This representation of the probability for the model parameters, age and Q
in, assumes that they are normally distributed around the preconception value, with a standard deviation of σage
and
![]() .
.
We expect the accumulation rate to vary smoothly along the flowband. Therefore the probability distribution for the accumulation-rate profile will be defined by its smoothness. The smoothness will be defined in scalar form by the integral along the flowband of the squared second derivative of the accumulation rate,
![]() , with respect to distance,
, with respect to distance,
![]() . Using a finite-difference representation of a uniform second-order derivative of the accumulation rate in the vicinity of xj
, the curvature can be expressed as (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007)
. Using a finite-difference representation of a uniform second-order derivative of the accumulation rate in the vicinity of xj
, the curvature can be expressed as (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007)

The probability distribution for the model parameter
![]() is defined as
is defined as

where
![]() is the a priori smoothness (equal to zero) and
is the a priori smoothness (equal to zero) and
![]() is the characteristic curvature of the accumulation-rate profile, given by
is the characteristic curvature of the accumulation-rate profile, given by
![]() , where
, where
![]() is a characteristic accumulation rate and l
(c) is a characteristic length scale for variability in the accumulation rate. The second term is a normal distribution, which is included to ensure that the probability distribution can be normalized. If this term is not included, an infinite number of sets of model parameters exist for which the first term will be of unity and the probability distribution can therefore not be normalized. The superscript ‘t’ represents the transpose of the model parameter vector.
is a characteristic accumulation rate and l
(c) is a characteristic length scale for variability in the accumulation rate. The second term is a normal distribution, which is included to ensure that the probability distribution can be normalized. If this term is not included, an infinite number of sets of model parameters exist for which the first term will be of unity and the probability distribution can therefore not be normalized. The superscript ‘t’ represents the transpose of the model parameter vector.
![]() is the covariance matrix for the
is the covariance matrix for the
![]() model parameters with only the diagonal being nonzero. Since the only purpose of this term is to ensure that the probability distribution can be normalized, the width of the normal distribution, exp
model parameters with only the diagonal being nonzero. Since the only purpose of this term is to ensure that the probability distribution can be normalized, the width of the normal distribution, exp
![]() , must be large enough that the solution is not affected. The total probability distribution for all the model parameters is the product of ρ
1(m) and ρ
2(m).
, must be large enough that the solution is not affected. The total probability distribution for all the model parameters is the product of ρ
1(m) and ρ
2(m).
Since the likelihood function in Equation (4) is reduced to the probability distribution for the calculated observable quantities,
![]() and the noise on the data is assumed to be Gaussian distributed, the likelihood is defined as
and the noise on the data is assumed to be Gaussian distributed, the likelihood is defined as
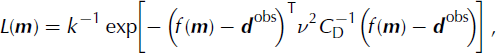
measuring how well the observable quantities based on a given model resemble the data. Here f(m) represents the forward algorithm coupling the model parameters with the observable quantities; d obs consist of the observed data given by the targeted internal layer, surface velocities at given points along the flowband and the estimated accumulation rate at the Taylor Mouth core site. These parameters are described in section 4.5. C D is the data covariance matrix. When the data parameters are statistically independent of each other, all the off-diagonal elements in the covariance matrix are zero. Along the diagonal is the variance for each of the data parameters. The scalar ν is a positive Lagrange multiplier, which is also called the ‘trade-off parameter’, because this value is adjusted until the misfit criterion defined in Equation (5) is satisfied. Adjusting the value of the Lagrange multiplier will adjust the balance between fitting the data and finding a smooth model for the accumulation pattern, with the values for age and Q in being within errors close to their preconception values.
4.2. Occam’s inversion
Occam’s inversion is conceptually similar to Tikhonov regularization, but instead of adjusting the influence of the data misfit on the result, the smoothness is adjusted. The strategy is to find the solution that fulfills the following constraints (Reference Gouveia and ScalesGouveia and Scales, 1997):
where R is a roughening operator, which calculates the second derivative of the model profile, and T is the tolerance on the observed data parameters, given by Equation (7). In our problem, the roughening operator applies only to the accumulation-rate profile, and not to our other model parameters. With these constraints we seek a set of model parameters where the accumulation profile is as smooth as possible, while keeping the data misfit below or at a given tolerance. The above constraints can easily be seen to be equivalent to the misfit criterion described in Equation (5). This means that only the features in the model that are required to fit the data will persist. The difference between Occam’s inversion and the Tikhonov regularization is in the influence of the Lagrange multiplier.
In Occam’s inversion, the Lagrange multiplier is included in the probability distribution for the accumulation-rate profile; in the Tikhonov regularization it is included in the likelihood function. This means that in Occam’s inversion the effect of the Lagrange multiplier is on the smoothness of the accumulation-rate profile, whereas in Tikhonov regularization its effect is on the data. Changing the value of the Lagrange multiplier enforces a greater or lesser degree of smoothing. This does not change the a priori confidence in the preconception values for the model parameters age and Q in or uncertainty in the data. Not changing confidence limits or standard deviations is appealing since it guarantees that the model parameters and data have the desired weights.
The probability distribution for the model parameters age and Q
in remains unchanged and is given by ρ
1 from Equation (8). The probability distribution for the model parameters
![]() is given by
is given by
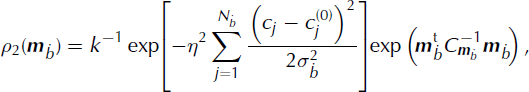
where η is the Lagrange multiplier. The probability distribution for all the model parameters is given by the product of ρ 1 and ρ 2. The likelihood function is given by

The Lagrange multiplier has been moved from the likelihood function in Equation (11) into Equation (14).
4.3. Bayesian inference
In contrast to Tikhonov regularization and Occam’s inversion, Bayesian inference does not assume that the accumulation-rate profile should be smooth. Instead, each model parameter has a probability distribution independent of the other model parameters, the same way the probability distribution for age and Q in is defined in the previous two methods (see Equation (8)). This means that all information regarding the data and model parameters is given as a probability distribution (Reference Gouveia and ScalesGouveia and Scales, 1997). For example, Reference Gudmundsson and RaymondGudmundsson and Raymond (2008) used a Bayesian inference method. Bayesian inference could be considered more objective because less personal opinion about the final solution to the problem is used to constrain the result of the MC simulation. This is obtained by omitting the Lagrange multiplier, letting the preconception values and associated confidence in those values dictate the solution(s) to the problem without forcing the solution to neither overfit nor underfit the data. A uniform value of the accumulation rate obtained from a local-layer approximation (LLA; Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007), averaged along the flowline, is our preconception value for the accumulation-rate profile. The LLA is calculated using a layer-thinning correction, assuming there are no horizontal gradients in geometry and strain rate. The accumulation-rate values are expected to be normally distributed about their preconception values. The probability distribution for the whole model parameter space is given by

where N
m is the number of model parameters and
![]() is the preconception value for the jth model parameter. The likelihood function is defined by Equation (15).
is the preconception value for the jth model parameter. The likelihood function is defined by Equation (15).
4.4. Model parameters and their confidence limits
The distributions of the model parameters age and Q
in are assumed to be Gaussian in all three MC formulations. Their preconception values are respectively age
(0) = 2000 years and
![]() per meter flowband width (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007). It is only in the Bayesian-inference formulation that the model parameters for the accumulation-rate profile are assumed to be normally distributed. In the cases where a model parameter is assumed to be normally distributed, the confidence limits on the model parameters have been estimated, a priori, and these limits are equivalent to the standard deviations of their distributions. The confidence limits can also be seen as an indication of the degree to which the preconception values may be trusted: the less trust in the preconception values, the larger the confidence limits. In all three formulations, the confidence limits (the standard deviations) on the model parameters age and Q
in are 400 years and 25 m3 a−1 per meter flowband width, respectively, as used by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007). For the accumulation-rate profile, the a priori curvature in the Tikhonov regularization and Occam’s inversion is assumed to be zero. The confidence limit is given by the ratio between the characteristic length scale for changes in the accumulation rate and the characteristic accumulation rate, given by L
(c) = 700 m and
per meter flowband width (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007). It is only in the Bayesian-inference formulation that the model parameters for the accumulation-rate profile are assumed to be normally distributed. In the cases where a model parameter is assumed to be normally distributed, the confidence limits on the model parameters have been estimated, a priori, and these limits are equivalent to the standard deviations of their distributions. The confidence limits can also be seen as an indication of the degree to which the preconception values may be trusted: the less trust in the preconception values, the larger the confidence limits. In all three formulations, the confidence limits (the standard deviations) on the model parameters age and Q
in are 400 years and 25 m3 a−1 per meter flowband width, respectively, as used by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007). For the accumulation-rate profile, the a priori curvature in the Tikhonov regularization and Occam’s inversion is assumed to be zero. The confidence limit is given by the ratio between the characteristic length scale for changes in the accumulation rate and the characteristic accumulation rate, given by L
(c) = 700 m and
![]() , respectively. In the Bayesian inference formulation the a priori value for the model parameters
, respectively. In the Bayesian inference formulation the a priori value for the model parameters
![]() is 0.074 m a−1 ice equivalent. This value has been estimated by averaging the LLA profile. The standard deviation for this value is 0.025 m a−1, as estimated from the standard deviation of the LLA profile.
is 0.074 m a−1 ice equivalent. This value has been estimated by averaging the LLA profile. The standard deviation for this value is 0.025 m a−1, as estimated from the standard deviation of the LLA profile.
4.5. Data and their uncertainties
The data that are used when calculating the likelihood in Equations (11) and (15) comprise three types: the continuous internal layer at a discrete number of points with a spacing of 200 m; the ice velocity at the Taylor Mouth core site and three other locations along the flowband; and the estimated accumulation rate at the core site (see Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007, for a detailed description of the data parameters). The internal layer is highlighted in Figure 2. Based on gross-β measurement of bomb fallout products, the yearly accumulation rate at the Taylor Mouth core site is estimated to be
![]() The uncertainties in the observed data are assumed to be normally distributed (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007); they will therefore be equivalent to the estimated standard deviation. All the uncertainties have been estimated by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007): ±5 m for the internal layer depth, ±0.05 m a−1 for the velocity data and ±0.01 m a−1 for the accumulation rate at the Taylor Mouth core site.
The uncertainties in the observed data are assumed to be normally distributed (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007); they will therefore be equivalent to the estimated standard deviation. All the uncertainties have been estimated by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007): ±5 m for the internal layer depth, ±0.05 m a−1 for the velocity data and ±0.01 m a−1 for the accumulation rate at the Taylor Mouth core site.
5. Monte Carlo Simulation
While Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) used the Gradient method to infer values of the model parameters based on the data, here we use the MC method. The difference between the two methods lies in the search algorithm. The search algorithm finds the set of values for the model parameters that form the solution to the formulated inverse problem. The Gradient method performs a local search, while the MC method performs a global search (Reference Mosegaard and TarantolaMosegaard and Tarantola, 1995). Performing a global search by systematically exploring the whole model space might be practical for low-dimensional spaces, but for spaces with higher dimensions this method can require unreasonable computation time (Reference Mosegaard and TarantolaMosegaard and Tarantola, 1995). To deal with this issue, we use the Metropolis algorithm (Reference Metropolis and UlamMetropolis and Ulam, 1949). The Metropolis algorithm samples models according to any a priori information we have about the model parameters, and according to the resemblance between their calculated observable quantities and the data. From the set of sampled models, the solution to the inverse problem can be inferred (e.g. Reference Geman and GemanGeman and Geman, 1984; Reference TarantolaTarantola, 2005). A key advantage of this MC method is that only one distribution of sampled models exists and, regardless of the starting point in the model space, the method always converges towards this stable distribution (Reference Kaipio, Kolehmainen, Somersalo and VauhkonenKaipio and others, 2000). The MC method is well suited to nonlinear problems because it has the ability to find all likely solutions, whereas the Gradient method finds only the solution most accessible to its starting guess.
5.1. The Metropolis algorithm
The sampled density of models from the model space using the Metropolis algorithm is proportional to the a posteriori probability distribution (Equation (3)) for the model parameters (Reference Mosegaard, Tarantola, Lee, Kanamori, Jennings and KisslingerMosegaard and Tarantola, 2002). An algorithm with this property is called an ‘importance-sampling’ algorithm. This algorithm has two major advantages: first, it avoids extensive sampling from low-probability areas, thereby saving computation time; second, it is not necessary to evaluate the whole a posteriori probability distribution, only the a posteriori probability for the sampled models (Reference Mosegaard, Tarantola, Lee, Kanamori, Jennings and KisslingerMosegaard and Tarantola, 2002).
The Metropolis algorithm performs a pseudo-random walk that consists of an exploration step and an exploitation step (Reference Mosegaard and SambridgeMosegaard and Sambridge, 2002). The exploration step jumps from the current model in the model space, denoted by m j , to the next model, m j +1. In practice this is done by first choosing a random model parameter from the whole set of model parameters and then perturbing the model parameter by a step whose size is given by a bounded symmetric uniform distribution centered around zero. The maximum size of this step is tuned such that an acceptance rate of 30–50% is obtained (Reference TarantolaTarantola, 2005). The goal is to choose as large a step size as possible while maintaining a high acceptance rate (Reference MosegaardMosegaard, 1998). During the exploration step, the algorithm decides whether to accept the perturbed model or to reject the perturbation and return to the previous model. The acceptance probability is given by (Reference Mosegaard and SambridgeMosegaard and Sambridge, 2002)
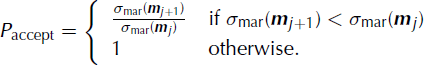
This means that if the a posteriori probability, σ mar(m), is increased by the exploration step, the random walk will definitely take the suggested step and the perturbed model, m k , will become the new current model. If the a posteriori probability has decreased, the perturbed model can still be accepted. The probability that the perturbed model is accepted is given by the ratio between the perturbed a posteriori probability, σ mar(m k ), and the present a posteriori probability, σ mar(m j ). If the perturbed model is not accepted, the random walk steps back to the current model, m j , and information about this model will be saved again and a new perturbation follows.
Since the initial model is often far away in the model space from the volume of interest, sampling begins after the burn-in time, as suggested by Reference Kaipio, Kolehmainen, Somersalo and VauhkonenKaipio and others (2000). The volume of interest is the volume where models generate high a posteriori probability and therefore this volume is sampled more often than areas of low a posteriori probability. The burn-in time can be determined by noting when the sampled a posteriori probability, as a function of the number of runs through the Metropolis algorithm since the start, reaches a relatively stable level. Another way of determining the burn-in time is by projecting the model space, including all sampled models, into a two-dimensional plane. By plotting two different model parameters versus each other, the burn-in time can be estimated by noting when the sampled models reach the area of interest, illustrated by a high density of sampled models. It can be seen that the sampled models move from the initial model in the model space in a direct path before reaching the area of interest, thereby illustrating the burn-in time.
In order for the sampled models to be statistically independent of each other, a waiting period between saving solutions has to be included. This is obtained by letting the sampling algorithm sample a number of models without actually saving them before saving the next model (e.g. Reference Dahl-JensenDahl-Jensen and others, 1998). The necessary number of runs between each pair of saved models for statistical independence is determined by the number of model parameters and by the nonlinearity of the forward algorithm.
5.2. Multiple solutions
If only one solution to the problem is present, working with the marginal distribution of each of the model parameters is possible. The marginal distribution of a model parameter is the frequency distribution of that model parameter. It is defined as the integral over the probability density distribution of the sampled models in the model space with respect to all model parameters except the specific model parameter for which the marginal distribution is calculated. Letting the probability density distribution of the sampled models in the model space be denoted by χ(m) and the model parameter for which the marginal distribution is calculated be mj , then the marginal distribution of mj is given by

where the integration is carried out over all the other model parameters except mj .
When several solutions in the form of several maxima in the a posteriori probability distribution are present, finding the mean and standard deviation from the marginal distribution for each of the model parameters is not a desirable method. This is because the solutions can ‘shade’ each other when calculating the marginal distribution so it can become difficult to determine the mean and standard deviation of the different solutions. Doing so may introduce errors and may not reveal any correct information about the solutions. Having more than three model parameters introduces a problem when trying to separate the solutions from each other, because simultaneous illustration of all the model parameters is not possible. An estimate of the number of solutions and the mean value of these solutions can be obtained by producing two-dimensional marginal distributions of pairs of model parameters. However, when there are more than a few model parameters, this procedure becomes computationally intensive since the number of different pairs of model parameters is given by N m!/[2(N m − 2)!]. It is possible to circumvent this problem by finding the mean and standard deviation of the multiple solutions in the high-dimensional model parameter space itself. Assuming that the distributions of the model parameters are normally distributed, we can use expectation maximization clustering. This clustering finds the mean and standard deviation for a pre-specified number of solutions. The mean and standard deviations are calculated such that the sum of the different N m-dimensional normal distributions for the various solutions approximates the sampled density distribution of the model parameters in the N m-dimensional model space (Reference MoonMoon, 1996).
5.3. Estimating the solutions
Using the forward algorithm of Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) and the available data for Taylor Mouth, we used the MC simulation to determine whether the a posteriori probability distribution is unimodal or multimodal. In the case of a multimodal a posteriori probability distribution, several possible solutions to the data can be inferred.
A posteriori probability distributions are sampled for different values of the Lagrange multiplier in the Tikhonov regularization and Occam’s inversion. The a posteriori probability distributions, σ mar(m), for the different values of the Lagrange multiplier can have one or several maxima. These maxima are inferred as possible solutions to the formulated inverse problem. The goal is to identify sets of model parameters that fulfill the misfit criterion (Equation (5)) from the possible solutions (i.e. maxima in the a posteriori probability distribution). In this way we regularize the inverse problem by demanding that the solutions neither overfit nor underfit the data. The sets of model parameters that fulfill the misfit criterion will then represent the solutions to the formulated inverse problem.
The a posteriori probability distribution is sampled for discrete values of the Lagrange multiplier. However, we seek solutions for which the misfit criterion (Equation (5)) is fulfilled, which is difficult to obtain with the use of sparsely spaced values of the Lagrange multiplier. Since it is computationally expensive to run the simulations with more values of the Lagrange multiplier, it is necessary to interpolate the a posteriori probability distributions to find solutions that satisfy the misfit criterion. Interpolating between N m-dimensional distributions is difficult because of problems visualizing high-dimensional spaces. Instead, we interpolate between the values of the misfit for the corresponding maxima in the a posteriori probability distributions corresponding to the different values of the Lagrange multiplier. This allows us to determine the values of the Lagrange multipliers for which the different solutions fulfill the misfit criterion. Once the values of the Lagrange multipliers are determined for the different solutions, the values of the model parameters corresponding to the different solutions can be found by interpolation. Before interpolating between the misfit for the corresponding maxima, the maxima of the different a posteriori probability distributions are divided into groups according to which solution they belong to. We do this by looking at the model parameters, age and Q in, and the evolution of their distributions for different values of the Lagrange multiplier.
6. Results
The misfit error, ||d||2 − T 2, as a function of the Lagrange multipliers, ν and η, for the different maxima in the a posteriori probability distribution, is shown in Figure 4a for Tikhonov regularization and Figure 4b for Occam’s inversion. Different shades of gray and markers are used in the figure to separate the maxima corresponding to different solutions. The misfit of the corresponding maxima in the a posteriori probability distribution is scattered because of uncertainties in the sampling of the a posteriori probability distribution. This uncertainty arises because the Metropolis algorithm has not been running for enough time to obtain a stable a posteriori probability distribution.

Fig. 4. Markers in (a) and (b) show misfit errors, ||d 2|| − T 2, associated with different maxima (identified by different shades of gray) in the a posteriori probability distribution, σ mar(m), as functions of the Lagrange multipliers, ν and η, for Tikhonov regularization and Occam’s inversion, respectively. Each solution to the inverse problem is found by tracking one maximum in σ mar(m) while varying the Lagrange multiplier, ν or η. Interpolation between the maxima for the different Lagrange multipliers is used to find the exact value of the Lagrange multiplier that fulfills the misfit criterion (Equation (5)). For example, the parameters age (c, d) and Q in (e, f) corresponding to each maximum in σ mar(m) are given by their values at the Lagrange multiplier for which the corresponding misfit error is zero in (a) or (b). The values are indicated by stars. Different shades of gray are used for the different solutions to the inverse problem.
Based on the fitted polynomial, the misfit error equal to zero in the Tikhonov regularization occurs for a Lagrange multiplier, ν, of 0.402 and 0.440 for the two solutions. For Occam’s inversion, the misfit error equal to zero occurs for a Lagrange multiplier, η, of 2.154, 2.332, 2.365 and 2.607 for the four solutions (see Table 2). Hereafter, the different solutions are identified by the value of the Lagrange multiplier for which the mismatch criterion (Equation (5)) is satisfied. Figure 4c and d show the age parameter for Tikhonov regularization and Occam’s inversion, respectively. Based on the fitted polynomial, the value of the age parameter is estimated for the values of the Lagrange multiplier where the misfit becomes zero. The determined values of the age parameter are marked by stars. The model parameter input flux, Q in, for different values of the Lagrange multiplier is shown in Figure 4e for Tikhonov regularization and Figure 4f for Occam’s inversion. The Q in parameter is analyzed in the same way as the age parameter, and values corresponding to a misfit equal to zero are indicated by stars. The accumulation-rate parameters are not shown, but their preferred values are inferred in the same way. The resulting accumulation-rate parameters are shown in Figure 5a and b.
Table 2. Values for age and Q in, and likelihood for the two solutions from Tikhonov regularization and for the four solutions from Occam’s inversion. For Bayesian inversion the solutions from the two simulations are close to being identical, except at the Taylor Mouth core site, so only one set of the values of the model parameters, age and Q in, is shown


Fig. 5. Mean values of the accumulation-rate parameters, spaced 200 m apart along the flowband, corresponding to the multiple maxima in the a posteriori probability distributions, σ mar(m), for (a) Tikhonov regularization and (b) Occam’s inversion, identified by the same gray shades as used in Figure 4. As in Figure 4, each solution is evaluated using the Lagrange multiplier that produces zero misfit error for the corresponding maximum in σ mar(m) (c) Two solutions were obtained with Bayesian inversion, with and without a preconception value for the accumulation rate at the Taylor Mouth core site. The position of the Taylor Mouth core site is shown with a vertical bar. The accumulation rate found here, based on gross-β measurement, was estimated to be 0.023 m a−1.
6.1. Tikhonov regularization
For Tikhonov regularization, the Lagrange multiplier, ν, is included in the likelihood function (Equation (11)). By changing the value of ν, the degree to which the model parameters recreate the observed data is adjusted. This is done by adjusting the weight that the data exert on the solution. The mean value of the accumulation-rate parameters along the flowband is shown in Figure 5a. The shape of the accumulation-rate profile is approximately the same for the two solutions, given by ν equal to 0.402 and 0.440, although the value of the accumulation rate is not. The values of the two solutions can vary by as much as 0.01 m a−1 along the flowline. This difference is counteracted by a difference in the corresponding age and Q in values, such that higher accumulation rates correspond to faster flow rates, and therefore a younger age for the targeted layer. The corresponding age and Q in values are listed in Table 2. The recreated layers based on the two solutions are shown in Figure 6. The figure illustrates that the large-scale structures of the layer are well resolved, but the structures smaller than ∼1 km are not. This is a result of the probability distribution given by the curvature of the accumulation-rate profile and the misfit criterion preventing the solution from overfitting the observed data.

Fig. 6. Shades of gray indicate layers calculated by the forward algorithm using corresponding accumulation-rate profiles in Figure 5. Thick gray band represents the targeted internal layer (data). In (a) and (b), values of Lagrange multipliers where the misfit criterion (Equation (5)) was satisfied distinguish the multiple solutions. In (c) the two layers shown correspond to Bayesian solutions with and without a preconception value for accumulation rate at the core site.
Particles that move past the end of the flowband before reaching their prescribed age reveal no information about the accumulation rate in the part of the flowband they pass. This means that particles started within the last ∼2 km of the flowband will reveal no information about the accumulation-rate pattern. Furthermore, since the effect of the accumulation-rate pattern is greater on particles near the surface than deeper down in the ice, the uncertainty on the estimated model parameters will increase along the flowband for this part, as seen in Figure 7, where the uncertainty seems to increase exponentially towards the end of the flowband, as information from shallow particles is missing.

Fig. 7. Standard-deviation profiles of the accumulation rate for Tikhonov regularization (solid curves), Occam’s inversion (dashed curves) and Bayesian inversion (dotted curves).
Since the speed of the flow increases along the flowband, the further down the flowband a particle is started the greater distance it will travel before reaching a given age. Since the final depth depends on the accumulation-rate history experienced, this implies that the uncertainty on the estimated accumulation-rate pattern will increase along the flowband, as seen in Figure 7. Furthermore, since the flow speed depends on the accumulation rate upstream of a given particle, uncertainties in the accumulation rate upstream will propagate into the flow speed and add uncertainty to the path of the particle. Right at the beginning of the flowband, few particles move through the ice, which results in the increased uncertainty, as seen in Figure 7. The uncertainty in the accumulation-rate solution is 5–10%, except at the beginning and end of the flowband, where it is higher because we are less able to resolve these values.
6.2. Occam’s inversion
Analysis of the sampled a posteriori probability distributions for the different Lagrange multipliers with Occam’s inversion shows that four solutions to the formulated inverse problem exist. The solutions are determined using the maxima in the sampled a posteriori probability distributions. The shape of the mean value of the accumulation-rate parameters along the flowband is very close to being the same as that for Tikhonov regularization, but the values are slightly lower. As with Tikhonov regularization, the uncertainties increase gradually in the downstream direction, then increase rapidly over the last 2 km of the flowband. The recreated layer is shown in Figure 6b. No significant differences can be seen between the recreated layers from Tikhonov regularization and Occam’s inversion. With this inverse method, all the large-scale features of the internal layer are recreated but small-scale structures are not produced by the chosen accumulation-rate profiles. As seen in Table 2, the age and Q in values are significantly higher in the solutions in Occam’s inversion than those derived with Tikhonov regularization. These higher values occur together with a lower accumulation-rate profile. The uncertainties for the solutions obtained using Occam’s inversion show the same features as seen for the solutions from Tikhonov regularization. However, here the values are ∼50% lower than for Tikhonov regularization.
6.3. Bayesian inference
In Tikhonov regularization and Occam’s inversion, a priori information and a smoothing constraint was applied to the model solution. In Bayesian inference, prior knowledge about the distribution of the model parameters is taken into account, but a smoothness constraint is not applied; the misfit criterion in Equation (5) is not applied either. Instead, the solutions are inferred solely from the a posteriori probability distribution, σ mar(m). Two simulations were performed, with and without the measured accumulation rate at the Taylor Mouth core site as a data parameter. In both simulations, a unimodal a posteriori probability distribution, σ mar(m), was found and therefore a single solution to the formulated inverse problem can be inferred for each simulation. Comparison of these two simulations shows the effect of the Taylor Mouth ice-core accumulation-rate data on the solution. The accumulation-rate profiles shown in Figure 5c are close to being identical for both simulations, only deviating significantly at the position of the core site. The general trend of the accumulation rate for Bayesian inversion is similar to the trend of the accumulation-rate profiles from Tikhonov regularization and Occam’s inversion. However, small-scale as well as large-scale structures in the accumulation-rate profile are present in the solution from Bayesian inversion. Both accumulation-rate profiles obtained using Bayesian inversion show a large decline at ∼2.5 km. This decline is present in order to reproduce the shoulder seen in the targeted internal layer in Figure 6. In the accumulation-rate profile corresponding to the simulation using the accumulation rate at the core site, a large decline is seen at the core site’s position. Since this decline is not seen in the accumulation-rate profile corresponding to the simulation without the use of the accumulation rate at the core site, the decline must be present because the confidence in the preconception value for the accumulation rate at the core site was too high.
The uncertainties, represented by the standard deviation of the accumulation-rate profile, are shown in Figure 7. They increase rapidly at the beginning of the flowband, after which they continue to increase slightly downstream. The recreated layers for both simulations are shown in Figure 6. Contrary to Tikhonov regularization and Occam’s inversion, Bayesian inference overfits the data because the data norm, ||d||, is less than the expected tolerance, T, calculated from the uncertainty in the data. The Bayesian formulation takes only the prior expectation and the data parameters and their uncertainty into consideration when finding solutions to the inverse problem. In this framework, whether the solution overfits or underfits the data is not an issue.
7. Discussion
Because of the computational requirements of the MC simulation, estimating the exact value of the Lagrange multiplier in Equation (11) or (14) that satisfies Equation (5) is expensive. A small uncertainty in the correct values for v and η for each solution must be tolerated. Existence of several maxima in the a posteriori probability distribution, σ mar(m), increases the complexity because the misfit criterion (Equation (5)) is fulfilled at different values of the Lagrange multipliers for the different solutions. An uncertainty in the sampled a posteriori probability distribution, σ mar(m), arises because a stable probability distribution is not always obtained. Removing this uncertainty requires the MC simulation to sample more models, thereby increasing the computational time. This uncertainty in the a posteriori probability distribution for the different values of the Lagrange multipliers results in an uncertainty in the determined Lagrange multipliers for which the solutions fulfill the misfit criterion.
When the sampled a posteriori probability distribution, σ mar(m), is multimodal, the likelihood that a given solution to a problem is the correct one can be estimated by the ratio of the number of sampled models attached to the cluster around that solution, to the total number of sampled models. Because of uncertainties in the sampling of models by the MC simulations, the ratio of sampled models in each cluster compared to the total of sampled models can vary when the Lagrange multiplier is changed. Since the solutions using Tikhonov regularization require different Lagrange multipliers, determining the likelihood of the individual solutions is difficult. The same problem applies to Occam’s inversion. Using Bayesian inference, no Lagrange multiplier exists. If the a posteriori probability distribution is multimodal, all solutions to the inverse problem can be inferred from the same probability distribution. The likelihoods of the different solutions are therefore better defined.
The likelihood that the solutions from Tikhonov regularization corresponding to v = 0.402 and 0.440 are correct is approximately 46% and 56%, respectively. The likelihoods do not add up to 100% because of uncertainties in sampling the a posteriori probability distributions, σ mar(m). For Occam’s inversion, the likelihood is 12%, 28%, 25% and 38%, respectively, for the solutions associated with η = 2.154, 2.332, 2.365 and 2.607. For Occam’s inversion there is, again, an uncertainty in sampling a posteriori probability distributions. From this it can be inferred that the solution corresponding to η = 2.607 is the most likely solution, while for Tikhonov regularization both solutions are close to being equally likely.
Using a Gradient method, Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) found age = 1703 years and Q in = 112 m3 a−1 per meter flowband width. Their solution is within one standard deviation of one of our solutions (v = 0.440, age = 1714 years) found with the MC method using Tikhonov regularization. The accumulation-rate profile inferred by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) corresponds to values partly from both the solutions found in the MC simulations. The solution of Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) is probably not at a maximum in the a posteriori probability distribution, but rather some model parameters were at a secondary maximum, while others reached the point in the model space corresponding to the absolute maximum a posteriori probability.
To eliminate multiple solutions from the MC simulation, more data are needed to constrain the solutions. For example, it would be possible to eliminate uncertainty in the model parameter Q in by starting the flowband at the ice divide, where the influx of ice is zero. Another way to constrain the influx, Q in, is to have a surface-velocity measurement near the upstream end of the flowband which could constrain uncertainty in Q in to within the measurement uncertainty of the surface-velocity measurement. In general, more surface-velocity measurements would constrain the solution of this inverse problem. If the age of the tracked internal layer was known (e.g. by absolute dating) and the accumulation-rate profile and the influx, Q in, were unknown, probably only one maximum would be present in the a posteriori probability distribution. The solution to the problem would therefore be well defined, and the problem would be well suited for the Gradient method.
The fundamental difference between formulations using Tikhonov regularization and Occam’s inversion is the way in which the Lagrange multiplier controls the solution. In Tikhonov regularization, the Lagrange multiplier influences the importance of recreating the data, thereby permitting the solution to be more or less smooth, as well as changing the degree of trust in the preconception values of age and Q in. In contrast, Occam’s inversion uses the Lagrange multiplier to directly control the degree of smoothness of the accumulation-rate profile and does not change the confidence in the preconception values of the parameters, age and Q in, while adjusting the Lagrange multiplier in order to fulfill the misfit criterion. This makes Occam’s inversion preferable. In a case where determining the age and Q in parameters is not part of the inverse problem, our formulations of Tikhonov regularization and Occam’s inversion are equivalent. The absence of a smoothing constraint in Bayesian inversion is clearly seen in the result: the accumulation-rate profile is much more variable. Using Bayesian inference, only observed data and probability distributions of the model parameters influence the solution. This means that Bayesian inference is less affected by a priori knowledge, since the smoothing constraint is not imposed. This, however, does not imply that the solution is more correct than the solutions from Tikhonov regularization and Occam’s inversion. Although short-wavelength features have been seen in shallow radar data, we think they are unlikely to persist for ∼1500 years, and we attribute the variations in the solution to the Bayesian inference to errors in the layer data. Formulating the inverse problem using Bayesian inversion reveals information about the solution at different spatial scales to the formulations based on Tikhonov regularization and Occam’s inversion.
When solving an inverse problem, not only the method used (e.g. Gradient or MC) but also the formulation of the problem is important, since it is in this step that any a priori constraints on the solution to the problem are introduced. One therefore has to decide whether or not the smoothness of a set of model parameters should be introduced in the probability distribution for the model parameters. If no smoothness constraint is introduced, the formulation of the problem could be carried out using Bayesian inference. Bayesian inference returns a solution that is dictated entirely by the observed data, and by the preconception values of the model parameters and their tolerances. This formulation is beneficial either if one fully trusts the theory relating model parameters to data parameters and trusts the observed data, or if one wishes to infer the information ignored or smoothed out by other methods. An example of extra information revealed by Bayesian inference can be seen in Figure 5, where we test the effect of introducing a preconception value for the accumulation rate at the Taylor Mouth core site. The decline in the accumulation rate at the core site, for the solution that includes the preconception value for the accumulation rate, shows that the average accumulation rate over the last 1500–1600 years is higher than the average accumulation rate from 1955 to 1995. This was noticed by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) and could also have been inferred from the solutions generated by our Tikhonov regularization and Occam’s inversion, but it is only once the smoothing constraint is removed that the difference between the average accumulation from 1955 to 1995 and that over the last ∼1500 years can be trusted. Furthermore, it can be seen that the accumulation rate on both sides of the core site has to increase to counteract the lower accumulation rate at the core site, which was forced to be there because of the preconception value.
Bayesian inference also suggests that the along-flow decrease in the accumulation rate at ∼8 km is steeper than suggested by the other formulations, where smoothing constraints are introduced. The Bayesian-inference solution also shows that locally low accumulation rate is required to recreate the shoulder seen in the tracked internal layer at ∼2.5 km. This could imply that the shoulder is caused by an error in the depth of the internal layer if, for example, the tracking algorithm jumped to a different layer at that point; to solve this would require full three-dimensional topography of the bed.
Each solution has a N m by N m correlation matrix, whose element in row i and column j describes how parameter i correlates with parameter j. This matrix then reveals information about the resolution of the model parameters. Correlation matrices for multiple solutions from the same formulation of the inverse problem are nearly identical, therefore only one correlation matrix from each method is shown in Figure 8. The first two model parameters in the correlation matrix are age and Q in. Model parameters 3–62 are the accumulation rates at 200 m intervals along the flowband. There are no major differences between the correlation matrices for Tikhonov regularization and Occam’s inversion. The correlation between an accumulation rate at a specific point and its adjacent points is similar in both formulations. It can be seen in Figure 8a and b that a band with high correlation values exists along the diagonal of the correlation matrix. This means that the accumulation rate at a specific point is not independent of the accumulation rate at the adjacent points. The size of the correlated neighborhood is determined by the characteristic width of this band, which gives a measure for the spatial resolution of the solution. This high correlation between adjacent points is probably a result of the smoothing constraint. Because of the high correlation between adjacent model parameters for the accumulation rate, it might be practical to decrease the number of accumulation-rate parameters along the flowband. This would not decrease the amount of information revealed by solving the inverse problem, but it would decrease the computation time.

Fig. 8. Correlation matrix for solutions from (a) Tikhonov regularization, (b) Occam’s inversion and (c) Bayesian inversion. The first two model parameters are age and Q in, respectively. Model parameters 3–62 are the accumulation-rate parameters at 200 m intervals along the flowband. Only one correlation matrix is shown for each formulation because the matrices for different solutions from each formulation are nearly identical. For Bayesian inversion, the correlation matrix corresponds to the simulation which includes a preconception value for the accumulation rate at the Taylor Mouth core site.
The correlation matrices also show that each accumulation-rate model parameter in the downstream half of the flowband is anticorrelated with the accumulation rate ∼1–2 km on each side. At larger offsets, there is very little or no correlation in the solution with Tikhonov regularization. Not surprisingly, a strong anticorrelation exists between the first model parameter (age) and the magnitude of the accumulation-rate profile. This is expected because higher accumulation rate along the flowband must result in a lower age of a layer at the same depth. This anticorrelation generally decreases along the flowband. This effect is illustrated by a resolving function, which becomes broader downstream of the flowband (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007). The resolving function characterizes the ability to recreate perturbations in the accumulation-rate pattern. There is a positive correlation between the age and Q in model parameters. This correlation is weaker in Bayesian inversion than in Tikhonov regularization and Occam’s inversion. Furthermore, since no smoothing constraint is applied to the accumulation-rate profile in the Bayesian inversion, the accumulation-rate parameters are not positively correlated with their adjacent points. On the contrary, they are negatively correlated with their adjacent points. This anticorrelation decreases along the flowband, except at the Taylor Mouth core site. As pointed out above, the accumulation rate at the core site is anticorrelated with the adjacent points. This anticorrelation indicates that the accumulation rate over the period 1955–94 measured by gross-β detection of bomb layers at the core site is much smaller than the average accumulation rate for the last 1500–1600 years, as inferred from the depth of the layer. As for Tikhonov regularization and Occam’s inversion, the age model parameter is anticorrelated with the accumulation-rate profile for the Bayesian inversion.
8. Conclusions
Although several solutions to the inverse problem may exist, depending on the formulation, the main features of the accumulation-rate profile are the same, independent of the formulation. The long-wavelength features are in agreement with the results of Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007), except at the downstream end of the flowband, where nearly all the solutions found by the MC simulation show increasing accumulation rate in the downstream direction. Only the solution corresponding to η = 2.607 in Occam’s inversion follows the trend found by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) in this part of the flowband. The solution corresponding to η = 2.607 is the most likely of the solutions (38% in Occam’s inversion). This indicates that the accumulation-rate parameters found in this region by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) are near the absolute maximum in the a posteriori probability distribution, σ mar(m).
We have shown that solutions to the inverse problem described by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) can differ in subtle ways, depending on the formulation, and within a particular formulation the solutions may again not be unique. This implies that introducing more data parameters could modify the solution from the Gradient method that is used by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007), and the MC method used here.
In addition, we find it is preferable to use the Gradient method since the computation time for the MC simulation is greater by a factor of 100. The Gradient method, however, carries the risk of finding only one out of several maxima in the a posteriori probability distribution and thereby not finding all likely solutions to the inverse problem. The MC method should, whenever possible, be used as an independent check on the results generated by the Gradient method.
The MC method also reveals information about the solution to the inverse problem that the Gradient method cannot, such as a well-defined uncertainty in the solution(s) and correlation coefficients between the various model parameters. This underlines the importance of using as many formulations as possible to solve an inverse problem. The solutions found with Tikhonov regularization, Occam’s inversion and Bayesian inference agree on the shape of the accumulation-rate profile, but they are inconsistent regarding the value of the age and Q in parameters, and thus the magnitude of the accumulation-rate profile. The value of the accumulation rate is more likely to be tightly constrained if the age of the layer is more constrained, or if more surface velocity data are available. The inverse problem presented here, and by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007), is a mixed ‘smallest’ and ‘smoothest’ problem, and we have argued that Occam’s inversion is a more appropriate formulation than Tikhonov regularization when a smoothing constraint is applied. Since we use a smoothing constraint, each accumulation-rate parameter is correlated with its neighbors. With this problem formulation, the correlation is found to be high, suggesting that the same information could be obtained while using fewer accumulation-rate model parameters, thereby reducing the computation time required by the MC simulation.
Acknowledgements
We thank Antarctic Support Associates for field logistical support and J. Dibb for gross-β accumulation-rate measurements. Reviewer O. Eisen and scientific editor R. Greve provided many helpful comments and suggestions. This work was supported by US National Science Foundation grants OPP-0440666 and OPP-9421644. H.C. Steen-Larsen thanks the following organizations for financial support during a six-month stay at University of Washington: Oticon Fonden; Niels Bohr Fondet; Karen Marie Louise Jensens Mindelegat; Hotelejer Anders Maansson og hustrus legat; Studenterhuset; and travel stipend from the Danish Geophysical Union.












