Introduction
The problem of describing the motion of a clast in the basal ice of a glacier lies at the heart of physically-based models of erosion and deposition. Order-of-magnitude calculations have been made by Reference LewisLewis (1960), who discussed the maximum force that could be exerted by a rock held in ice, and by Reference Boulton, Wright and MoseleyBoulton ([c1975]), who adapted Reference WeertmanWeertman’s (1957) sliding theory to produce a condition for the onset of abrasion. Reference RöthlisbergerRöthlisberger (1968) identified and described the processes which tend to bring clasts into contact with the bed. Full analytical solutions for the motion of isolated clasts in ice unbounded by other solid surfaces have been obtained by Reference Glen, Glen, Donner and WestGlen and others (1957), to explain the preferred orientation of the long axes of clasts in the direction of flow of a glacier, and by Reference WattsWatts (unpublished), in order to derive equivalent viscosities for dilute suspensions of particles in ice. This paper describes an analytical solution for the flow of ice past a solid object and over an external solid boundary. The analysis indicates that interaction between processes occurring on the glacier bed and on the surface of a clast in the basal ice will produce effects which have not been considered in previous calculations.
Figure 1 shows the simple two-dimensional problem that will be analysed in this paper. A long cylindrical stone with circular cross-section, radius R, lies in the ice at the point x = 0, y = ∆. The stone lies in an area zone (i) where the glacier bed and the surface of the ice are horizontal planes, y = 0 and y = H. Up- and down-stream, in zones (ii) and (iii), the glacier bed is undulating and has an overall slope. We shall suppose that the boundaries of zone (i) are far enough from the origin for the ice flow not to be affected by the presence of the stone.

Fig. 1. A cylindrical stone radius R lying a distance ∆ from a plane rock surface in ice of thickness H.
In basal-sliding theories dealing with clean ice (Reference WeertmanWeertman, 1957; Reference LliboutryLliboutry, 1968; Reference NyeNye, 1969, Reference Nye1970; Reference KambKamb, 1970) it is usual to assume that a lubricating “regelation layer” of water exists between ice and bed-rock. Thus, locally, the shear stress at the ice–rock interface is zero. However, if the bed undulates about a given base plane the ice exerts a net force on the rock which can be interpreted as the result of an average shear stress acting over the base plane. In zones (ii) and (iii) there is an average shear stress between the ice and the undulating bed. In zone (i) we will suppose that the bed can be given an effective or “magic” roughness for part or all of its area, despite the fact that geometrically it is treated as a flat plane. This means that the shear stress on this part of the boundary y = 0 can take non-zero values. Thus, the transition between the region of flow over an effectively rough bed and the region of flow around the smooth stone and over a smooth bed is independent of the choice of the extent of zone (i). This allows a physically reasonable description of the boundary conditions on y = 0 to be combined with simple boundary conditions describing the velocity distribution in the ice at the boundaries between zones (i), (ii), and (iii). The geometry of this problem has been specified in such a way that the two boundaries at which the physical processes are most complicated, the ice–rock interfaces, are coordinate curves in the bipolar coordinate system.
Suppose that in zones (ii) and (iii) the ice moves under gravity with a steady-state flow pattern which depends on the shape of the bed and the depth of the ice. In general there will not be a steady-state situation in zone (i), for, unless the stone is at rest with respect to the bed or moves in such a way that the separation ∆ is maintained, the pattern of flow must change with the change in the relative positions of the ice–rock interfaces. This problem does not arise in the analysis of the motion of isolated clasts in ice.
For the sake of making a relatively simple first analysis, it is assumed in this paper that forces — X, —Y and a couple L oppose the forces X, Y, and couple L exerted by the ice so that a steady-state situation is maintained. Thus, only a small sub-set of the possible solutions for the motion of the ice and stone is being considered. The set of solutions with X = 0, L = 0, and — Y equal to the weight of the stone is physically possible. Other solutions are artificial, but the direction of the resultant force that would have to be applied to the stone, in order to maintain its position with respect to the bed, gives an indication of the direction in which the stone would tend to move in the real situation where gravity is the only force acting at a distance on it.
Reference Boulton, Wright and MoseleyBoulton ([c1975]) derives a condition for the lodgement of a stone on a glacier bed by estimating the horizontal force exerted on the stone by the ice and equating this to the retarding friction between stone and bed. Strictly speaking, the analysis in this paper cannot be applied to a stone in contact with the bed. However, if the stone is extremely close to the bed, i.e. when ∆ ≈ R, we might postulate the existence of a very small irregularity on the stone which allows normal and frictional forces to be transmitted without disturbing the pattern of flow of the ice or altering the physical processes at the boundaries. Then we might hope to derive a more accurate estimate of the lodgement condition, based on an analytical solution for the forces of the ice on the stone rather than an order-of-magnitude calculation.
The Navier–Stokes equations in bipolar coordinates
The bipolar coordinates α, β are defined in terms of the Cartesian coordinates x, y by the equations

The coordinate curves are two sets of coaxial circles (Fig. 2) which intersect orthogonally. The scale factor a is the distance between the point α = ∞ and the line α = 0 (the x-axis). The metric coefficient is

Elements of arc have lengths δα/h, δβ/h. The radius of the circle α = α 1, is R = a/sinhα 1, and the distance of its centre from the line α = 0 is ∆ = a|coth α 1|. In this coordinate system, the Navier–Stokes equations for the slow steady flow of a linearly viscous incompressible fluid under gravity are
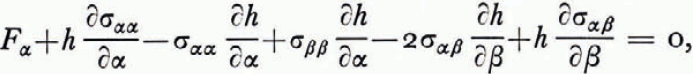
and

Fα and Fβ are the components of the body force which can be derived from the hydrostatic pressure p 1

If the line α = 0 is horizontal, then

where p 1 = p b is constant on α = 0, ρ is the density of the ice, and g the acceleration due to gravity.

Fig. 2. The bipolar coordinate system.
The components of the stress tensor σ ij are related to the components of the strain-rate tensor ė ij by the equations

where η is the viscosity and p is a pressure term. The continuity equation is

where uα is the velocity in the α direction and uβ the velocity in the β direction. Thus, a stream function ψ may be defined by the equations

The Navier–Stokes and continuity equations reduce to the biharmonic equation for the stream function
and the Laplace equation for the pressure p
The general solution for the biharmonic equation in bipolar coordinates has been given by Reference JefferyJeffrey (1920, Reference Jeffery1922)

where the Fourier coefficients ɸn , Χn are functions of α:

Since p and η∇2
Ѱ are conjugate functions, an expression for p in terms of the constants ![]() etc., can be derived. The leading term is 2η(B
0+D
1) β/a. Since p must on physical grounds be single-valued with β,
etc., can be derived. The leading term is 2η(B
0+D
1) β/a. Since p must on physical grounds be single-valued with β,
The components of the strain-rate tensor can be expressed in terms of ψ

and hence, using Equations (12) and (13), may also be written as Fourier series in β with coefficients that are functions of the hψ coefficients An, An ′, etc. From Equation (6), p 1 may also be expanded in a Fourier series

Hence, from Equation (7), the components of the stress tensor may be expanded in Fourier series with coefficients that are functions of the hψ coefficients.
Boundary conditions
Figure 1 shows a cylindrical stone, radius R, at a distance ∆ from the horizontal bed of a glacier. The surfaces of the stone and bed are defined by the curves α = α 1, α = 0 respectively. The equation of the upper surface of the ice is

Up- and down-stream boundaries are defined by the equation
The coefficients in Equations (13) are determined by applying boundary conditions to these five curves.
(i) The ice–rock interfaces
Conditions at these interfaces will be described in terms of the “classical” regelation theory (Reference NyeNye, 1967) although laboratory experiments have shown that this theory is oversimplified (Reference Nunn and RowellNunn and Rowell, 1967; Reference Townsend and VickeryTownsend and Vickery, 1967; Reference Drake and ShreveDrake and Shreve, 1973; Reference MorrisMorris, 1976). Drake and Shreve have pointed out that the effect of impurities, supercooling, and the formation of a trace must be included in a complete regelation analysis. However, we use the simple theory since it allows a simple and clear mathematical demonstration of a difficulty which I believe would arise in any case. In this geometry the classical regelation analysis proceeds as follows: Between ice and rock on the surfaces α = o, α = α 1 there are thin films of water, the regelation layers. On the boundary between the ice and the stone (α = α 1) there is no shear stress;
On part of the boundary between the ice and the bed we may want to allow a non-zero shear stress τ produced by the effective roughness. Thus

where β 1 and β 2 are arbitrary constants.
This boundary condition can be written in the form of a Fourier expansion for σαβ,

on the surface α = 0.
In areas where the normal pressure on the rock is high, ice melts and the water travels through the regelation layer to the areas of low normal pressure. The ice–water interfaces are always at the melting-point temperature, which varies with the stress normal to the interface. Thus
where C is a constant having the value 0.7 x 10–7 deg Pa–1.
The high-pressure areas have a lower temperature than the low-pressure areas. Thus the latent heat released by the ice when it refreezes in the low-pressure areas flows through ice, stone, and bed to melt more ice in the high-pressure areas.
The velocity of the ice in the positive direction is

The latent heat released by freezing per unit time on an element δβ/h is Luαδβ/h on α = 0 and —Luαδβ/h on α = α 1, L is the latent heat of melting of ice per unit volume (2.8 X 108 J m–3). Let T i, T s, T b be the temperature distributions in the ice, stone, and bed respectively, and k i, k r the thermal conductivities of the ice and rock. Then, on α = 0,

and on α = α 1

In the classical regelation analysis the temperature distributions are solutions of the Poisson equation with boundary conditions given by Equations (24) and (25), and the restriction that the temperature should remain finite as α → 0, β → 0 (i.e. as x → ∞, y → ∞) and as α → ± ∞.
The distributions have the form


and

Using Equation (22) the T coefficients, En , Gn , etc., can be denned in terms of the hѱ coefficients. Then Equations (24) and (25) give sets of equations relating groups of the hѱ coefficients. Further equations are derived from the boundary conditions (19) and (21) for the shear stress. We arrive finally at sets of linear equations from which all the hѱ coefficients may be determined given A 0, B 0, C 0, D 0, B 1, A 2, C 2, A 3, C 3, A 1′, B 1′, C 1′, D 1′, A 2′, and C 2′. The further equations which determine the values of these last coefficients are derived from other boundary conditions.
(ii) The ice-air. interface
Since H ⪢ a we have α → 0, β→ 0 on the upper surface of the glacier. The expansions for p and ėαα reduce to

Therefore, from Equation (7) the boundary condition
reduces to

Now h → 0 as α and β → 0 so huα → 0, hѱ → 0 if uα and ѱ remain finite on y = H. We may therefore specify two more conditions

(iii) The up-stream and down-stream boundaries
In a complete analysis of glacier flow the gravitational forces which produce motion in the ice are determined from the slope of the bed and/or the upper surface of the ice (e.g. Reference MorlandMorland, 1976). We have focussed attention on a small horizontal area of the bed over which the ice has a uniform thickness. We have to suppose that up-stream and down-stream of this area gravitational forces act so as to produce a certain pattern of flow of the ice as it enters and leaves the area of interest around the stone. This pattern is defined by boundary conditions on x = ±X 1. For example, we might suppose that far away from the stone there is simple shear flow parallel to the bed. Thus, for example,

where u b is the sliding velocity at the bed.
Forces on the stone
Let the forces applied to the surface α = α 1 be statically equivalent to forces X and Y acting at the centre of the stone and a couple L. X acts in the direction parallel to the bed and Y in the perpendicular direction

On the surface of the stone σα β = 0. From Equations (22) and (26), using the series expansions

Expressions for the forces may be obtained in terms of the T coefficients which are themselves known in terms of the hѱ coefficients. Thus,

Discussion
The solution of the equations relating the coefficients of the series expansion for hѱ (Equation (12)) is discussed in the Appendix. It is found that the series of coefficients {ɸn } and {ѱn } diverge, unless both λ⋆ and λ⋆′ (two dimensionless critical wavelengths) are zero. Given that L, C, k r, k i, and η are known, finite, and non-zero physical constants, this condition means that a → ∞ and the ratio of the distance of the radius of the stone to the distance of its centre from the bed R/ ∆ → 0. In other words, a solution exists for an isolated cylinder in ice (and has indeed been given by Reference WattsWatts (unpublished)), but not when there is another solid boundary.
Thus, we have found that, in the steady state, the classic regelation boundary conditions cannot be obeyed both at a flat bed and at the surface of a circular stone. That is, the temperature and stress distributions cannot be matched so that both the surfaces are at the pressure-melting point. A similar problem has arisen before in theoretical work on regelation and has been discussed by Reference NyeNye (1967) and Reference MorrisMorris (1976). In their analyses, for wires and spheres moving through ice and for ice moving around a cylinder with a wavy surface respectively, there is apparently only one boundary at which normal stress and temperature must be matched. However, at any point within the ice where there is a water inclusion, for example at a three-grain intersection, a relation between, the normal stress across the interface and the temperature can also be defined. Thus there are internal boundaries to be considered. Morris suggested that melting and refreezing within the ice would produce an “internal” temperature distribution to be added to the “regelation” temperature distribution which is produced by melting and refreezing on the solid boundary. The total temperature distribution would match the stress distribution so that the ice is always at the pressure-melting point. The classic method of analysis of regelation problems depends on the assumption that any “internal” component of temperature is negligible compared to the “regelation” component at the solid boundary.
I suggest that, even in the time-dependent case, when there are two solid boundaries with melting and refreezing on each there is no reason to suppose that the temperature and stress distributions can be matched so that the ice at both surfaces is at the pressure melting point. There are three ways in which this problem could be resolved:
-
(1) melting and refreezing within the ice could produce an “internal” temperature distribution such that the ice at the two boundaries and at the internal water inclusions was at the pressure-melting point. The magnitude of the internal heat sources and sinks would not be negligible compared to the magnitude of the sources and sinks on the boundaries;
-
(2) the ice could separate from the boundaries producing water-filled cavities with shapes such that the temperature at the ice–water interface was always the correct melting-point temperature for the normal stress across the interface. At the moment we do not know if there is any shape for which a steady-state solution is mathematically possible given our formulation of the problem with linearly viscous ice and classical regelation boundary conditions;
-
(3) the ice could separate from the boundaries producing cavities filled with air and/or water vapour. In this case, parts of the boundary where there is no melting can be well below the pressure-melting point and the requirement that stress and temperature distributions should match at all points of the boundaries is relaxed.
Field observations of clasts in basal ice (e.g. Reference Vivian and BocquetVivian and Bocquet, 1973; Reference Boulton, Boulton, Morris, Armstrong and ThomasBoulton and others, 1979) indicate that cavities frequently occur in the lee of large particles. Some of these cavities are full of water, others have long spicules of clear ice. The habit of these ice crystals suggests that they may have grown into a cold atmosphere which is below the pressure-melting point.
Of course, the conditions at the bed of a glacier are vastly more complicated than the simple problem that has been analysed in this paper. We have, for example, ignored the effect of geothermal heating, drainage of water at the glacier bed, and the interaction between several clasts in transport which may obscure the effects of the stress–temperature adjustment process described here. The classical regelation theory used in this paper and in current basal sliding and lodgement theories is known to be inadequate. However, two conclusions can be drawn which are important for theories of erosion and deposition:
-
1. Cavities may form around clasts in transport in the basal ice because of the presence of the bed. These cavities must be distinguished from those produced by “cavitation” Reference Nye(Nye, 1970) which is controlled by the overburden pressure of ice.
-
2. The size and shape of such cavities will depend on the pattern of flow of the ice. If the stone moves to a part of the bed with a different flow pattern, or the pattern at a given point changes in time, bulk melting or refreezing must take place as the cavities adjust to the new situation.
Thus, we cannot expect that the forces on a stone due to the ice can be calculated by a simple application of classic regelation and plastic-flow theory. Even when the clast is in contact with the bed and there is only one ice–rock boundary there may not be solutions of the partial differential equations for ѱ and T if regelation boundary conditions are applied along the whole of the boundary. Reference Happel and BrennerHappel and Brenner ([c1973], p. 61) remark that it is difficult to generalize on the required conditions for the existence of unique solutions to the Navier–Stokes equations given combinations of prescribed velocities and derivatives at the boundary. We know there are solutions for the rather odd mixed boundary conditions that arise from classical regelation theory when these are applied on spherical, cylindrical, and plane surfaces (note that in Nye’s solution for a perturbed plane and the Morris adaptation of this for a perturbed circular cylinder the boundary conditions are applied at the unperturbed surface). However, these are rather special geometries in which the orthogonal curvilinear coordinate system defined by the boundary curve has metric coefficients which do not vary with position along the boundary. Whether solutions exist for Newtonian flow of ice over rock humps or clasts of any shape resting on the bed with classic regelation conditions applied over the whole boundary is an open question.
I do not believe that the problem of the adjustment of stress and temperature distributions that has been raised in this paper is an artefact of the particular geometry, flow law, and boundary conditions chosen. The simplifications I have made merely allow a clear analytical demonstration of the need for an adjustment process. This process will almost certainly occur whenever there are two ice–rock interfaces close together and may also have a part to play in a complete description of flow over steep bedrock obstacles.
Appendix
This Appendix gives the derivation of the coefficients of ɸ n for high n. Similar equations hold for the coefficients of Xn . For low values of n some terms of the equations are lost or altered but the overall form is the same.
The shear-stress boundary conditions (Equations (21) and (19)) lead to

and

The normal stress boundary conditions lead to equations for the T coefficients


Ri and Si are functions of n, cosh nα 1 and sinh nα 1:

and
If ux /h expanded in the Fourier series

and

the velocity boundary conditions (Equations (24) and (25)) give

and

Substitution for Fn and Hn from Equations (A-3) and (A-4) into Equations (A-7) and (A-8) gives

and

λ⋆ and λ⋆′ are dimensionless critical wavelengths which may be compared to the critical wavelength given by Reference NyeNye (1969):

and

Now, from Equation (9)

hence from Equations (A-5) and (A-6)

and

Substitution for ρ i and ϒ i from Equations (A-9) and (A-10) and for B i and D i from Equations (A-1) and (A-2) using i = n — 3, n+3 leads to two simultaneous equations for A n+3 and C n+3 in terms of the known coefficients A n-3 to A n+2 and C n-3 to C n+2. Note that some coefficients are functions of λ⋆ or λ⋆′, others depend only on α 1.
Discussion
J. Weertman: Do your boundary conditions take into account the surplus, unfrozen water that is left over after the regelation cycle is completed? The volume of this water produced per unit time should be equal to the work done per unit time divided by the latent heat of melting–freezing per unit volume of ice. You could not obtain a consistent set of equations that could give a steady-state solution for this problem. But if water is continuously produced by the regelation cycle—which is a Carnot cycle—the problem cannot be a steady-state one.
E. M. Morris: My boundary conditions are those used by other authors such as G. S. Boulton and B. Hallet, since I am trying to investigate the validity of their order-of-magnitude analysis. I agree that the regelation equations used by these authors are inadequate.




