Introduction
Quantifying glacier terminus change in a consistent and accurate way is crucial for the accurate monitoring of glacier and ice-sheet dynamics over timescales ranging from days to centuries. Multiple methodologies have previously been applied to this problem, each with its own advantages and shortcomings. However, different methods can provide conflicting results when analysing the same glacier termini. As studies are increasingly applying single methods over large geographical areas, trying to quantify terminus change without knowledge of methodological limitations could result in the unnecessary introduction of errors. This is particularly relevant to studies of Greenland, where retreat of tidewater glacier termini has been both significant and widespread (Reference Moon and JoughinMoon and Joughin, 2008; Reference Box and DeckerBox and Decker, 2011; Reference Howat and EddyHowat and Eddy, 2011; Reference Jiskoot, Juhlin, St Pierre and CitterioJiskoot and others, 2012; Reference Mernild, Malmros, Yde and KnudsenMernild and others, 2012), especially over decadal to centennial timescales (Reference Bevan, Luckman and MurrayBevan and others, 2012; Reference BjørkBjørk and others, 2012). However, the methods discussed below are also of considerable relevance for monitoring tidewater and land-terminating terminus change in the other glaciated regions of the world (see, e.g., Reference Cook, Fox, Vaughan and FerrignoCook and others, 2005; Reference VanLooy and ForsterVanLooy and Forster, 2008; Reference Lopez, Chevallier, Favier, Pouyaud, Ordenes and OerlemansLopez and others, 2010; Reference BraunBraun and others, 2011; Reference Davies, Carrivick, Glasser, Hambrey and SmellieDavies and others, 2012).
In the majority of cases the inconsistencies and inaccuracies between methods will be small. However, where changes in glacier orientation, width or unusual margin geometries occur, significant errors can occur. Under certain circumstances these may render some methods unsuitable for tracking terminus change. Therefore understanding which method is likely to yield the most accurate results in a given scenario is crucial when deciding which methodology to employ. This decision should be based on the aims of the study, the level of detail required and a comprehensive awareness of the advantages and limitations of each methodology. This will allow glacier terminus position to be tracked with greater confidence, and data of greater relevance to the study to be collected. The issues highlighted here are primarily relevant to tidewater calving margins, where terminus geometry can be highly dynamic, and terminus positions can change by several kilometres within a single year. Calving glacier margins account for ~50% of mass loss from Greenland (Reference Van den BroekeVan den Broeke and others, 2009) and almost all Antarctic mass loss (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011), making the accurate tracking of calving margins crucial to improving our understanding of the drivers of and controls on dynamics and terminus stability (Reference MurrayMurray and others, 2010; Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011, 2012; Reference Christoffersen, O’Leary, Van Angelen and Van den BroekeChristoffersen and others, 2012).
Existing methodologies that are commonly used to track fluctuations of tidewater calving margins are applied to a range of idealized and real glacier scenarios to evaluate their ability to accurately track terminus retreats of varying complexity. We also present and evaluate two new methods of tracking terminus change: (1) a modification of the ‘box’ method (Reference Moon and JoughinMoon and Joughin, 2008; Reference Howat and EddyHowat and Eddy, 2011) that aims to increase its range of applicability and accuracy, and (2) a method that accounts for the position of the full terminus length relative to the glacier centre line. All the methods are simple to apply using standard tools available in ArcGIS v10.1 (Environmental Systems Research Institute).
Methods of Tracking Terminus Change
Multiple methods have previously been employed to track changes in calving margin position. The aim of these has been to reduce terminus position to a one-dimensional (1-D) value representing the distance the glacier has advanced/retreated along its flow axis. The methods that will be analysed in this study are summarized below.
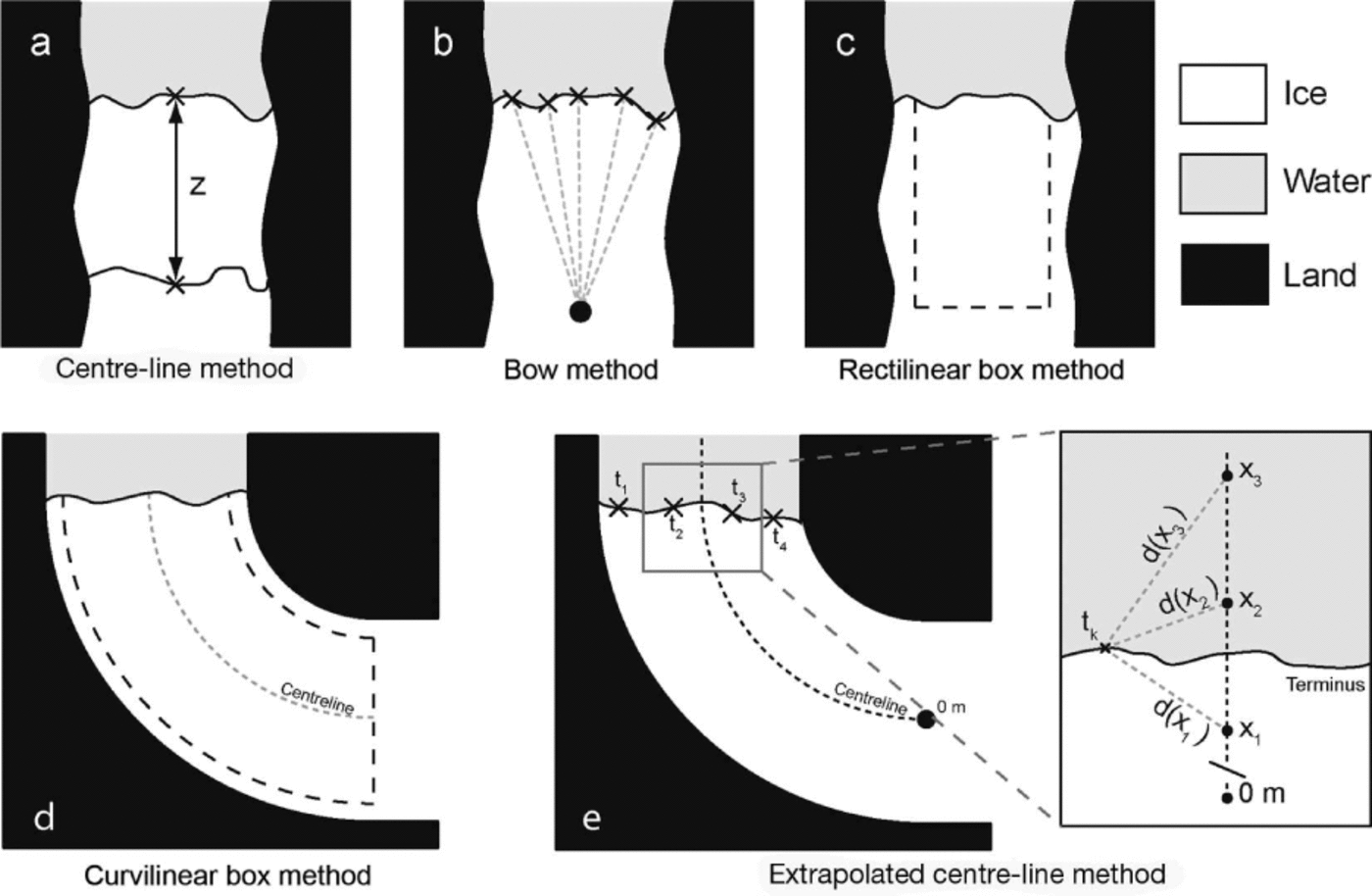
The centre-line method measures the distance between the centre of successive terminus observations along the glacier flow axis (Fig. 1a; Reference Bevan, Luckman and MurrayBevan and others, 2012; Reference Mernild, Malmros, Yde and KnudsenMernild and others, 2012; Reference Walsh, Howat and Ahn Yand EnderlinWalsh and others, 2012). Definition of the glacier centre line will depend on the aims of a particular study. For example, the centre line can be defined either through manual estimation, as the topographic centre line, or the fastest flow axis of the glacier, while automated methods for determining glacier length have also been employed (see, e.g., Reference LeBris and PaulLe Bris and Paul, 2013). In this study, all methods that require a centre line use the topographic centre line, defined as the line representing the midpoint between the lateral ice and fjord margins for the observation where the ice is at its greatest extent. This can be determined easily and quickly by delineating the glacier margins and tracing the line following the maximum Euclidean distance between these margins down to the glacier terminus. Results of analyses undertaken in this study will be relevant to centre-line-dependent methods irrespective of the centre-line definition used.

Fig.1. Different methods used to ascertain glacier terminus position relative to a fixed point/baseline: (a) Centre-line method showing a straight-line retreat of the terminus centre point by z. (b) Bow method, showing the reference point and the position on the terminus from where measurements are taken (the position of the reference point relative to the ice front is for illustrative purposes, since it would normally be at least six ice widths from the terminus). (c) Rectilinear box method. (d) Curvilinear box method tracking the glacier centre line. (e) Extrapolated centre-line method, with inset showing a generalized case of how positions on the glacier centre line, xn , are related to individual points on the terminus, tk , with the linear distances between them shown by d (xn ). The inset shows tk calculated using xn values taken from a centre-line distance range equivalent to the distance between x 1 and x 3.
The bow method determines terminus position relative to a fixed reference point positioned six or more glacier widths upstream of the farthest retreated terminus (Reference BjørkBjørk and others, 2012). At distances of six or more glacier widths upstream Reference BjørkBjørk and others, (2012) found that terminus change results for a subset of glaciers were convergent. Measurement points are spaced at predetermined distances along the user-delineated terminus, with the average linear distance between these and the reference point giving the overall terminus position (Fig. 1b). Glacier change can be calculated by differencing the relative position values for different termini.
The rectilinear box method quantifies the change in area between terminus observations of a fixed-width rectilinear box drawn over the glacier trunk. This is then converted to a 1-D value representing width-averaged terminus change by dividing the area by the width of the box (Fig. 1c; Reference Howat and EddyHowat and Eddy, 2011). This is a variation on the method of Reference Moon and JoughinMoon and Joughin, (2008), who tracked terminus change using boxes that were allowed to have straight, non-parallel sides. The effect of non-parallel sides on results would ideally need correcting for, requiring extra calculations to account for the changing box width for each observation. Further complexities also arise as a result of the multiple different ways in which box width could be defined, each potentially providing different results for the same termini. For these reasons, and the desire for methodological simplicity, clarity and accuracy, we evaluate only the fixed-width rectilinear box method (hereafter rectilinear box method), since the definition of box width is unambiguous.
The curvilinear box method is as above, but instead of the fixed-width box being rectilinear, it is curvilinear. This provides a notable advantage over the rectilinear box method in that it allows changes in fjord orientation to be accounted for (Fig. 1d). This is achieved by generating a box of fixed width tracking the glacier centre line.
The extrapolated centre-line method utilizes inverse distance weighting (IDW; Reference Shepard, Rosenberg and BlueShepard, 1968) to extrapolate positions from the glacier centre line across the complete width of the fjord, allowing the relative position of a terminus to be quantified. This method also allows terminus change to be tracked irrespective of changing fjord width or orientation. Terminus position is determined by averaging the position of points spaced at regular intervals along a user-delineated terminus. The position of each of these points on the terminus, tk , is an IDW extrapolation calculated from centre-line points representing distances of xn along the centre line (Fig. 1e). The calculation of tk first requires determining the weighting value, w, to be allocated for each value of xn , such that

where d xn ð Þ is the linear distance between xn and tk and p is the power parameter, which is generally taken to be 2 (Reference Shepard, Rosenberg and BlueShepard, 1968). Each value of w xn ð Þ is then normalized so that values of xn can be extrapolated laterally without tending towards zero with increasing distance from the centre line. This allows each value of tk to have an equal weighting in the calculation of the overall terminus position, such that

Then this can be used to calculate tk according to

where m is the number of centre-line positions (i.e. xn values) used in the calculation. The overall terminus position, T, can then be calculated, such that for q observations of t

The value of T represents the average distance of the entire terminus from the beginning of the centre line (Fig. 1e). However, the method in this form without modification is vulnerable to having its results skewed where the centre line is long, and numerous values of xn occur distal to tk . To account for this, a search radius for tk is defined, which limits the number of xn values used in its calculation to a subset. This consists of the xn values with the lowest associated d (xn ) values within a defined search radius. The value of m is therefore dependent on the number of xn values that fall within the search radius. The minimum search radius that should be used for calculation of tk is determined as part of the experiments conducted below.
This method can easily be applied in ArcMap v10.1 using the IDW tool to create a raster surface representing the extrapolated centre line, from which T can be calculated for each terminus by extracting the mean z values.
Glacier Configurations Tested
Experiments were designed to test the accuracy of each method when subject to different terminus geometries and changes in fjord orientation. By using idealized scenarios rather than comparisons with previously published data, analytical difficulties due to irregular terminus/fjord geometries, differences in user delineation of glacier termini and image resolution are avoided. This allows errors that result solely from the methodologies to be analysed. Finally each method is applied to tracking examples of actual glacier termini, and differences in the results are analysed with reference to the idealized scenarios.
Idealized glacier scenarios
Figure 2 displays the seven idealized glacier retreat scenarios tested. Each scenario was constructed so that a terminus undergoes a width-averaged retreat of R. For simplicity, R is taken to be equal to a single glacier width, W. All results are referred to in terms of glacier retreat, though the inverse of the results from these tests will be relevant for equivalent glacier advances. The experiment scenarios constructed are:

Fig. 2. Experiments showing the idealized scenarios, where R is an identical width-averaged retreat for each experiment. The letters of each experiment conform to those indicated in the text. The grey dashed line indicates a width-averaged retreat of R parallel to the original terminus. Where the rectilinear box method is applied to experiments (e)–(g), the box is orientated so that the upstream edge of the box is both parallel to, and centred on, the black dashed line indicated. Unless specified in the text, the curvilinear box used for experiments (e)–(g) is of width W and tracks the fjord width.
-
(a) Retreat of a linear terminus by R to form a new parallel terminus in a straight fjord (Fig. 2a).
-
(b) Width-averaged retreat of a linear terminus by R to form a new symmetric terminus with a calving bay of 0.25R in a straight fjord (Fig. 2b).
-
(c) Width-averaged retreat of a linear terminus by R to form a new asymmetric terminus, with the asymmetry hinged on the centre line (at 0.5W), and a calving bay of 0.25R in a straight fjord (Fig. 2c).
-
(d) Width-averaged retreat of a linear terminus by R to form a new asymmetric terminus, with the asymmetry offset from the centre line by 0.25W, and a calving bay of 0.5R in a straight fjord (Fig. 2d).
-
(e) Width-averaged retreat of a linear terminus by R to form a new parallel terminus in a fjord that has changed orientation. The retreated terminus is offset to the right by 0.5W (Fig. 2e).
-
(f) As for (e), but the retreated terminus is positioned perpendicular to the fjord wall (Fig. 2f).
-
(g) As for (e), but the retreated terminus has a calving bay of 0.25R symmetric along the glacier centre line (Fig. 2g).
In reality, the challenge of tracking glacier terminus change reflects a combination of some or all of the above scenarios
Real glacier examples
To allow an intercomparison of results from the different methods, six Greenlandic tidewater glaciers exhibiting a range of retreat behaviour were selected for analysis (Fig. 3). Together they exemplify a number of potentially problematic scenarios that can arise when tracking change of real termini. The glaciers selected were Narssap Sermia (NS; 64.648 N, 49.978 W), Jakobshavn Isbræ (JI; 68.178 N, 49.858 W), Petermann Glacier (PG; 80.788 N, 60.618 W), Helheim Glacier (HG; 68.618 N, 32.938 W), Qalerallit Sermia West 1 (QSW1) and Qalerallit Sermia West 2 (QSW2) (61.048 N 46.728 W). Some of the issues with the retreat of these glaciers include: the terminus of NS changes orientation within the fjord, and demonstrates asymmetry and increasing complexity across the time series analysed; the width of JI changes significantly during its retreat, while embayments with relatively stagnant ice also exist; the terminus of PG is an ice shelf, meaning that periodically large calving events of tabular icebergs occur, and identification of the terminus itself can be problematic; HG is a fast-flowing glacier retreating through a straight fjord that experiences significant changes in terminus geometry; and QSW retreats from being a single glacier to form two separate termini that are analysed separately (named here as QSW1 and QSW2).

Fig. 3. Landsat-based observations of terminus change at six Greenlandic glaciers, and the results given by different methods of tracking terminus change (inset). Glaciers shown are (a) Narssap Sermia (64.648 N, 49.978 W), (b) Jakobshavn Isbræ (68.178 N, 49.858 W), (c) Petermann Glacier (80.788 N, 60.618 W), (d) Helheim Glacier (68.618 N, 32.938 W) and (e) Qalerallit Sermia West 1 and Qalerallit Sermia West 2 (61.048 N, 46.728 W). The rectilinear and curvilinear boxes used to track terminus change are overlaid on the images. Box width was limited to that of the narrowest terminus observation.
For each glacier, five terminus positions acquired between 1992 and 2012 were delineated from Landsat panchromatic band (15 m pixel resolution) images, and terminus change quantified using each method. For JI and HG, images were preselected for the period after the melange in their fjord had broken up to allow easier definition of their termini. Termini were delineated at a level of image magnification that allowed individual pixels to be visually resolved. This allowed a consistent level of detail to be maintained when delineating individual termini from different glaciers.
NS was subject to extra experiments (below) to demonstrate how the bow and box methods deal with issues pertaining to terminus asymmetry, width and fjord orientation when applied to real glaciers. Its terminus retreated significantly between 2009 and 2012, having previously maintained an approximately stable terminus position since the end of the Little Ice Age (Fig. 4; Weidick and others; 2012). To allow the relative effects of a change in fjord orientation to be fully evaluated, a straight terminus of semi-arbitrary orientation was also positioned upstream of the 2012 terminus (terminus A; Fig. 4).

Fig. 4. Location map of Narssap Sermia showing the reference points used in the bow method indicated by the red crosses, and their associated offsets from a semi-arbitrary 08 position centred on terminus A. Each reference point is positioned at least 6W from terminus A. The background Landsat image shown was acquired on 15 September 1987. Dates are day/month/year.
Experiments
Terminus change was calculated for all the scenarios outlined, according to the methodologies described above. To allow full interrogation of the methods, additional method-specific experiments were also undertaken for the bow, box and extrapolated centre-line methods as described below.
Bow method experiment
The distance between the reference and measurement points used for the bow method is known to exert control on the accuracy and consistency of its results (Reference BjørkBjørk and others, 2012). However, the effect of the reference point positions relative to fjord and terminus orientations has not been established. Consequently, the range of effects that could result from changes in fjord orientation upstream of the termini was evaluated by quantifying terminus change for experiments (a)– (g) using 19 different reference points positioned 6W behind the terminus distributed evenly along a 1808 arc at 108 intervals. This experiment was also conducted over the same range of reference points for NS to demonstrate how reference point position can affect results for real termini (Fig. 4). Although the majority of fjord orientations will change by significantly less than 908 from their original terminus orientation, testing a large range of reference point positions allows the effects of a comprehensive range of potential changes in fjord orientation to be evaluated. The points on the termini used in the calculation of overall position were spaced along each terminus at equidistant 0.01W intervals for scenarios (a)–(g) and 10 m intervals for NS.
Box method experiment
One of the primary advantages of the box methods is that they are capable of accounting for the natural asymmetry of glacier termini (Reference Moon and JoughinMoon and Joughin, 2008). However, since it is necessary to use boxes of fixed width for the method, it is inevitable that parts of the fjord terminus margins will fall either outside or inside the predefined box. To test the relative importance of this, boxes of 0.25–2W width (with 0.25W increments) were applied to scenarios (a)–(g), while boxes of 1–7 km width (with 1 km increments) were applied to NS. This was done for both the rectilinear and curvilinear box methods. Where the terminus end of the box was wider than the delineated glacier terminus, the box was closed by extending the terminus edges with straight lines perpendicular to the upstream edge of the box for the rectilinear box method, and with lines perpendicular to the centre line of the box for the curvilinear box method.
he aim of this experiment is to test the sensitivity of both box methods to the proportion of the glacier terminus that is included in the calculation of terminus change.
Extrapolated centre-line experiment
To allow the method to be evaluated in a non-dimensionalized manner for experiments (a)–(g), the search radius that defines the number of xn values used in the calculation of each tk value needs to be defined in a clear and consistent way. This experiment aims to determine over what scales of search radii calculated terminus positions begin to converge, so that the value of the search radius can be standardized. Different search radii were tested, from a minimum using individual xn values in the calculation of tk , to ranges of xn values taken over a centre-line distance of 3W. These are then applied to the scenarios (e)–(g) where termini retreat a distance of R through a fjord that has changed orientation and exhibit different terminus geometries. Terminus position was calculated from points positioned on the terminus at 0.01W intervals, while points representing values of xn on the centre line were also separated by 0.01W.
Results
Centre-line method
While simple and quick to implement, the centre-line method does not account for the full complexity of terminus geometries, and hence cannot provide an accurate value of width-averaged retreat. This is highlighted in experiments (b), (c), (d) and (g), where the method overestimates terminus retreat (Table 1). Terminus geometry therefore exerts a strong control on the accuracy and applicability of the centre-line method.
Table 1. Summary of results from each method after application to each of the idealized scenarios shown in Figure 2. Results for rectilinear and curvilinear box methods are for box widths of W only. All results are given in terms of R

Bow method
The bow method accurately calculates width-averaged retreat for experiments (a) and (b), but underestimates terminus retreat in the remaining scenarios (Table 1). When compared with Figure 5a, underestimates for experiments (e)–(g) are caused by the position of the reference point relative to the change in fjord orientation. In these cases, the correct retreat value is obtained for reference points offset 408 from the original (Fig. 5a). A line from this reference point will be orientated perpendicular to the termini of experiments (e)–(g). The error produced by the method can be significant depending on the position of the reference point used to measure terminus retreat, with the –808 and –908 offsets of experiments (e)–(g) even showing the terminus to have advanced (Fig. 5a).

Fig. 5. Results of experiments testing the sensitivity of (a) the bow method to changes in the position of the reference point from which measurements are taken and (b) the rectilinear box method and (c) the curvilinear box method to different box widths. The results are from each method applied to the experiments shown in Figure 2.
The bow method also underestimates retreat for experiment (c), and more significantly for experiment (d), where the retreated terminus has a more pronounced asymmetry (Table 1). The results curves are also laterally offset towards the relative position of terminus asymmetry, compared with the results of experiments (a) and (b) (Fig. 5a). This offset is greater for the more asymmetric experiment (d), indicating that terminus asymmetry also exerts a control on the relative accuracy of the technique. However, the effects of terminus asymmetry are markedly less significant than that of the relative positioning of the reference point.
Rectilinear and curvilinear box methods
Where box width equals terminus width, the curvilinear box method successfully measures width-averaged retreat across all scenarios, while the rectilinear box method demonstrates a dependence on fjord orientation (experiment (e)) and terminus geometry (experiment (f)); Table 1). The results from the curvilinear box method for experiments (f) and (g) replicated the results from experiments (a) and (b) for the rectilinear method. This demonstrates that the curvilinear method accurately accounts for changing fjord orientation, provided that the box width is identical to that of the terminus (Fig. 5c; Table 1).
Where the boxes were less than the full glacier width, terminus geometry dictated the accuracy of both the rectilinear and curvilinear box methods (Fig. 5b and c). For box widths greater than the idealized terminus widths, the curvilinear box method consistently underestimated retreat, with the scale of this underestimation increasing with box width (Fig. 5c). The overall magnitude of underestimation by the curvilinear box method is dependent on terminus geometry, with only linear termini (experiments (a), (e) and (f)) being unaffected. By comparison, terminus geometry and changing fjord orientation can result in the rectilinear box method producing both under- and overestimates where the box is wider than the glacier terminus being measured.
Extrapolated centre-line method
The initial extrapolated centre-line method experiment shows that changing the ranges of xn values used to calculate values of tk has minimal effect, with a 2.5% range of results observed (Fig. 6). As the search radius increases towards W, the method becomes more accurate across all experiment scenarios, with search radii >W producing generally concordant results (Fig. 6). Consequently, for subsequent analyses, values of tk were calculated using the nearest xn values taken from a stretch of the centre line of W length. This was also used for the application of the extrapolated centre-line method to NS (where W 5 km).

Fig. 6. Results testing sensitivity of the extrapolated centre-line method to the different ranges of xn values used in the calculation of tk and how that affects overall calculated terminus position
The results of the extrapolated centre-line method demonstrate that it succeeds in accurately calculating terminus retreat where termini are symmetrical, but underestimates retreat where termini are asymmetric (Table 1). Comparing the results of experiment (c) with experiment (d), the error increases with asymmetry, though the magnitude of this is still 5% (Table 1). This demonstrates that the method is capable of accounting for changes in fjord orientation, though it is prone to small errors where complex terminus geometries occur.
Narssap Sermia experiments
As observed with scenarios (a)–(g), results given by the bow method for NS are also dependent on the positioning of the reference point relative to the termini (Figs 4 and 7a). For all box sizes tested, the general pattern of retreat calculated by both box methods is comparable (Fig. 7b and c). Where the box widths are less than the terminus width of NS (5 km), the two box methods generate different values since the boxes have different orientations. Therefore, even though the boxes may have identical widths, the two methods will be tracking change between different sections of the termini. Nevertheless, both the curvilinear and rectilinear box methods produce very similar results for the retreat of NS from 2009 to 2012 (Fig. 7b and c). However, where the fjord changes orientation for 2012-terminus A, the value from the rectilinear box method disagrees with that from the curvilinear box method, exceeding it by 339 m (Fig. 3a).

Fig. 7. Comparison of results tracking the change of Narssap Sermia, showing the sensitivity of (a) the bow method to changes in the position of the reference point from which measurements are taken and (b) the rectilinear box method and (c) the curvilinear box method to different box widths.
For the bow method no single reference point from the 1808 arc displays results comparable with the box or centre-line methods for the entire record from 2009-terminus A (Fig. 7). However, a similar pattern and magnitude of change can be extracted from the bow method by using the results of all the reference points in the 1808 arc and taking the single largest retreat value for each year to create a record of terminus change (Fig. 7).
Different box widths display no systematic behaviour of over- or underestimation between the different NS terminus observations (Fig. 7b and c). This is probably a result of differing terminus geometries between observations. A change of fjord orientation can be ruled out as a causal factor of this since, for the period 2009–12, retreat occurs in a relatively straight section of the fjord (Fig. 4). Where the boxes are less than the full terminus width (i.e. <5 km), the magnitude of terminus-change values is reduced. Boxes that overlap the fjord edges (i.e. >5 km) tend to display the extreme upper and lower values for terminus change (Fig. 7b and c).
Real glacier method intercomparison
Figure 3 shows the results of different methods applied to the termini of six Greenlandic tidewater glaciers. There is significant variability in the results, with no method displaying a consistent bias for under- or overestimation compared with others. In most cases each method produces the same general pattern of terminus change, though the absolute numbers can vary considerably, with examples of discrepancies up to 1.94 km at HG (2003–05) and 4.76 km at PG (2009–12; Fig. 3c and d). In some cases the methods identify differing patterns of retreat, an example being the bow and extrapolated centre-line method results contrasting with those of the other three methods at QSW1 after its terminus becomes diffluent from QSW2 (Fig. 3e). The bow method also estimates significantly less retreat compared with the others at NS (a difference of up to 1.67 km), after the termini change orientation by 2011 (Fig. 3a). Prior to this, terminus observations are positioned directly behind the bow method reference point, with these results being more concordant with other methods compared with subsequent observations. A further notable discrepancy occurs at JI, where the centre-line method estimates an advance (84 m between 2005 and 2012), with other methods estimating a retreat of 1.58–3.12 km.
Discussion
Overall, the analyses above allow a distinction to be made between three broad styles of measuring glacier terminus change along a flow axis, namely, 1-D terminus change (e.g. centre-line method), length-averaged change (e.g. bow and extrapolated centre-line methods) and area/width-averaged change (e.g. rectilinear and curvilinear box methods). When deciding which to apply, the choice should primarily be based on an explicit justification of which method is capable of providing the most relevant data to fulfil the aims of a study. Factors that need to be considered with respect to this include (1) whether using a method that quantifies length-averaged change or area/width-averaged change is relevant to the aims of the study, (2) the level of detail required, (3) the importance of accounting for changes in terminus width, (4) any changes in fjord orientation, (5) whether terminus geometries display significant asymmetry or complexity and (6) whether a specific definition of the centre line or flow axis could significantly affect results. Table 2 provides a summary of scenarios in which each method is, and is not, reliable in providing accurate results. Given the importance of terminus-setting variability, the decision as to which method to use should only be made after all termini have been delineated. This will allow comprehensive evaluation of whether certain methods may be comparatively more susceptible to error for particular terminus settings.
Table 2. Summary of situations for which each method is capable of accurately accounting, and whether results may be dependent on how a centre line is defined. Asterisks highlight that the bow and extrapolated centre-line methods do have some dependence on terminus geometry, though this is in most cases negligible

An example scenario would be if areas of stagnant/slow-flowing ice are not relevant to a study. In such situations, including terminus margins (where the occurrence of stagnant ice is most common) may not be necessary and may lead to the inclusion of irrelevant information in the data collected. The curvilinear box method may be best suited to such scenarios, given its ability to account for changing orientation along a flow axis. However, if significant width changes occur, the extrapolated centre-line method could also be usefully applied. This would be relevant if the part of the terminus that is of interest (e.g. ice flowing above a certain velocity) is not of a fixed width.
Evaluation of methods
The centre-line method has been shown to be the least broadly applicable method over a range of scenarios (Table 2). Results from scenarios (a)–(g) demonstrate that it is incapable of determining width-averaged terminus change, and commonly displays little absolute agreement with any other method (Table 1; Fig. 3). Conversely, the method is possibly the quickest and easiest to implement, and mostly successfully identifies the general pattern of terminus change on the real-world glacier examples (Fig. 3). However, considerable caution should be exercised in the application of this method since it is prone to significant error in both absolute and relative terms. It is vulnerable to substantial under- and overestimation of terminus change depending on terminus geometry, recording an advance at JI of 84 m between 2005 and 2012, when the terminus had clearly substantially retreated (Fig. 3b). The ability of the method to account for changes in fjord orientation provides an advantage over the rectilinear box and bow methods, which are both constrained by fixed frames of reference. The centre-line method should therefore be considered useful as a method for gaining cursory insight into the large-scale changes occurring at a glacier terminus, though owing to its inability to reflect width-averaged change, its application to detailed studies of tidewater terminus dynamics should be avoided. It is more suited to tracking changes at land-terminating margins where terminus response is likely to be more symmetric (see, e.g., Reference Lopez, Chevallier, Favier, Pouyaud, Ordenes and OerlemansLopez and others, 2010; Reference Leclercq and OerlemansLeclercq and Oerlemans, 2012).
The sensitivity of the bow method to terminus shape, fjord orientation and reference point positioning is demonstrated by the results of both idealized (Table 1; Fig. 5a) and real glacier analyses (Figs 3 and 7a). While the general pattern of retreat can be extracted from an arc of reference points, as exemplified by results from NS (Fig. 7a), this adds complexity to the method, requiring extra calculation and user input, thus compromising its simplicity. Furthermore, since the bow method calculates terminus position using straight-line distances from the reference point, it is unable to accurately track terminus change directly along the glacier flow axis when fjord orientation changes. In these situations the method will underestimate the along-glacier distance between the reference point and positions on the terminus. This is likely to be even more significant for smaller non-ice-sheet glaciers where changes in fjord/valley orientation compared with their overall size can be considerable.
Although scenarios (c) and (d) show that effects of terminus asymmetry on the accuracy of the bow method are small, the impacts of the relative positioning of the reference point on the end results are significant. The bow method should only be applied on straight glaciers, where the termini to be measured are near-linear and approximately parallel, otherwise the positioning of the reference point may significantly affect results. This is demonstrated by results from NS where termini change orientation and are highly asymmetric (Fig. 4).
Both the rectilinear and curvilinear box methods performed well in tracking the terminus change of glaciers of uniform width, though results from the idealized and real scenarios indicate that the latter has wider applicability (Table 1; Figs 3 and 5b and c). When tracking NS terminus change using different box widths, the larger spread of values given by the curvilinear box method compared with the rectilinear method can be accounted for by the two methods measuring different sections of the termini (Figs 4 and 7b and c). This is because the centre of the rectilinear box will differ from the curvilinear box, as the latter tracks the glacier centre line while the former is indirectly defined by the user when the rectilinear box is drawn. This demonstrates how terminus geometry can significantly affect box method results where the entire width of the glacier is not used to calculate terminus change (Fig. 5b and c). This was a significant problem for NS, JI, HG, QSW1 and QSW2 where box widths (limited in size to the narrowest terminus observation) were in some cases unable to cover significant fractions of the delineated termini. This is best exemplified at QSW1, where the pattern of terminus retreat differed significantly from the bow and extrapolated centre-line methods that account for full glacier widths (Fig. 3e).
Conversely, where termini are of roughly uniform width, the curvilinear box method is fully capable of tracking fjord orientation changes and accounting for complex terminus geometries (Tables 1 and 2; Fig. 3c). Owing to its inability to track changes in fjord orientation, the rectilinear box method should only be applied where glaciers retreat through a straight fjord.
It is worth noting that a further variation on the box method could potentially account for changes in glacier width and orientation. This would be achieved through dividing the terminus area into multiple adjoining boxes that are (1) orientated parallel with one another, (2) of equal ‘b –axis’ length (i.e. short axis approximately parallel with flow axis) and (3) of variable ‘a –axis’ length (i.e. long axis approximately perpendicular to flow axis), allowing changes in fjord width and orientation to be tracked. The accuracy of the method would also improve as the ‘b –axis’ length is decreased and the fjord geometry is more accurately captured by the boxes. Application of this method is complex compared with the other methods discussed, and hence beyond the confines of this study; however, if it could be automated then it would prove a highly accurate method of tracking area/width-averaged terminus change.
The extrapolated centre-line method performs well where termini are regular, and successfully tracks most asymmetric and complex termini with minimal error (Table 1; Fig. 3). It was anticipated that significant issues with terminus asymmetry and/or complexity may arise when tracking the termini of glaciers such as PG, where the margins are often comparatively fractured. This means that a significant fraction of the total length of their termini can be located near their margins (Fig. 3c). The effect of this would be to disproportionately weight the terminus position towards the terminus position of the ice margins. However, results for PG proved comparable with other methods (Fig. 3c). Nevertheless, this is an issue that should be considered before applying the method to termini with significantly fractured margins. Elsewhere the effect of terminus asymmetry will be less significant, with the idealized retreats showing an error of <5% (Table 1; Fig. 6). In most cases, this will lie within the operator delineation error.
Notable advantages of the extrapolated centre-line method include its ability to account for the entire terminus length irrespective of changes in glacier width, in addition to changes in fjord orientation. This proved to be especially useful where advance/retreat occurs through a glacier or fjord confluence such as at QSW, or where the terminus area of interest may change between observations.
Finally, the absolute uncertainty surrounding the delineation of each individual terminus position is worth brief consideration. If a given terminus observation is delineated multiple times, and the range of values determined, the absolute error will be different for each method for similar reasons to those outlined above. Nevertheless, where imagery such as Landsat or MODIS (Moderate Resolution Imaging Spectroradiometer) is used, the absolute error values in the delineation of individual termini are likely to be negligible compared with the absolute differences given by different terminus change methods (Fig. 3).
Conclusions
When selecting a method to track glacier terminus change it is important to consider the aims of the study, and the limitations of each method with regard to changes in glacier width, fjord orientation and terminus geometry. Each method was tested using idealized scenarios designed to highlight potential shortcomings, and hence indicate under which situations each method can confidently be applied. The methods were also applied to real glacier scenarios to highlight where methods can show disagreement, in addition to some of the practical issues that affect terminus tracking. From the results presented, the curvilinear box method accurately measures width-averaged retreat, though it is unable to fully account for changes in glacier width without incorporating some error. The extrapolated centreline method also performed well in a wide range of scenarios, successfully tracking changes in fjord orientation, width and terminus geometries with minimal associated error. Although potential caveats apply for its application to calving margins similar to PG, results generated were comparable to those of the curvilinear box method for the termini analysed.
These two methodologies represent improvements on existing methods as they fully account for changes in fjord orientation. However, since the extrapolated centre-line method is the only method that can directly account for changing fjord orientation, width and terminus geometry, it represents the most accurate method over the widest range of scenarios. The simplicity of the method also means that results can be generated easily and rapidly in only a few steps within GIS software packages such as ArcMap for any set of delineated glacier termini. This simplicity and range of applicability is important if attempts are made to track terminus changes across multiple glaciers at regional to continental scale using a single method.
Different methods can still be applied with confidence depending on the level of detail required for a study, the topic of interest and whether individual glacier terminus settings have been carefully evaluated. However, it is likely that such studies should either be looking at coarse-scale changes or be limited in the number of termini they seek to analyse. While results produced may be acceptable, using the extrapolated centre-line method will provide a high level of accuracy, is applicable across the majority of settings and minimizes the risk of introducing potentially significant methodological error into results.
Acknowledgements
The authors thank two anonymous reviewers for constructive comments that helped to improve the manuscript. This research was financially supported by J.M.L.’s PhD funding from UK Natural Environment Research Council grant No. NE/I528742/1.