1. INTRODUCTION
Snow slab avalanche release occurs as the result of failure initiation and crack propagation along a weak layer buried in the snowpack. When an initial crack in the weak layer reaches a critical size r c, it rapidly propagates resulting in the progressive fracture of the weak layer inducing its volumetric collapse (e.g. van Herwijnen and others, Reference van Herwijnen, Schweizer and Heierli2010). Avalanche release is thus a fracture mechanical process (e.g. McClung, Reference McClung1981).
The theory of fracture mechanics describes the separation of solids due to crack growth under external loading (e.g. Anderson, Reference Anderson1995). While the theory of fracture mechanics is far from complete, the field of linear elastic fracture mechanics has matured. Linear elasticity is the simplest form of material behavior, in which the stress and the strain in a material under uniaxial loading are related by the elastic modulus E = σ/ε. The overall aim of fracture mechanics is to assess the integrity of a structure in the presence of flaws (cracks), in particular to assess the crack size at which the energy available for crack growth exceeds the energy expended to extend the crack. To evaluate this critical crack size, it is convenient to use the energy release rate. It is defined as the rate of change in total energy per unit crack area (e.g. Anderson, Reference Anderson1995), i.e. a measure of the energy available to advance the crack by a unit area. Note that the energy release rate is with respect to crack length, not time. In an infinite uniform plate with a crack of length 2r subjected to a stress σ, the energy release rate G for linear elastic material is given by
At the onset of spontaneous crack propagation, when r = r c, the energy release rate G c equals the material resistance to unstable crack propagation: G c = 2w f, where w f is a material property called the specific fracture energy. It represents the energy that must be supplied to create a unit area of new crack surface (e.g. Bažant and Planas, Reference Bažant and Planas1998).
Applying Eqn (1) to cracks in a natural snow cover is not readily possible. First, snow is not a uniform material, as large density and microstructural depth variations are commonly observed. Interfacial fracture mechanics, which deals with crack growth between dissimilar materials, is thus more relevant to describe avalanche release (e.g. Schweizer and Camponovo, Reference Schweizer and Camponovo2002). However, due to the complexity of the interface problem, there are only a few analytical solutions available for special geometries (e.g. Hutchinson and Suo, Reference Hutchinson and Suo1992). Second, snow is a highly rate-dependent material, i.e. it generally does not behave like a linear elastic material. The fracture behavior of snow is thus best described as quasi-brittle, implying that the fracture process zone, a nonelastic zone ahead of the crack tip, is of finite size (Bažant and others, Reference Bažant, Zi and McClung2003; McClung, Reference McClung2009). Clearly, applying linear elastic fracture mechanics to snow does not account for the complex material behavior of snow. However, applying nonlinear theories requires additional material properties, such as the size of the fracture process zone and knowledge on the post-peak failure behavior (McClung, Reference McClung2015), which thus far remain unknown. Therefore, snow is still often treated as a linear elastic material. To assess the critical crack size for propagation in a layered snowpack consisting of a slab and the underlying weak snow layer, various theories have been proposed (e.g. McClung, Reference McClung1979; Chiaia and others, Reference Chiaia, Cornetti and Frigo2008; Heierli and others, Reference Heierli, Gumbsch and Zaiser2008; Gaume and others, Reference Gaume, Chambon, Eckert and Naaim2013). These all require knowledge of two material properties, namely the elastic modulus of the slab and the specific fracture energy (or strength) of the weak layer.
Our present knowledge on the elastic modulus of snow is mainly based on laboratory experiments. Mellor (Reference Mellor1975) reported values of the Young's modulus between 0.2 and 20 MPa for a snow density varying from 100 to 350 kg m−3. Most of these values were obtained from uniaxial compression experiments at very low strain rates
![]() $ \dot {\rm \varepsilon} $
between 8 × 10−6 s−1 and 4 × 10−4 s−1. More recently, Scapozza (Reference Scapozza2004) found similar values from quasi-static uniaxial compression tests (strain rate
$ \dot {\rm \varepsilon} $
between 8 × 10−6 s−1 and 4 × 10−4 s−1. More recently, Scapozza (Reference Scapozza2004) found similar values from quasi-static uniaxial compression tests (strain rate
![]() $ \dot {\rm \varepsilon} \lt 10^{ - 3} \,{\rm s}^{ - 1} $
). In contrast, Sigrist (Reference Sigrist2006) found significantly higher values by conducting dynamic loading experiments at high strain rates
$ \dot {\rm \varepsilon} \lt 10^{ - 3} \,{\rm s}^{ - 1} $
). In contrast, Sigrist (Reference Sigrist2006) found significantly higher values by conducting dynamic loading experiments at high strain rates
![]() $ \dot{\rm \varepsilon} \gt 10^{ - 2} \,{\rm s}^{ - 1} $
, and even higher values were reported by Capelli and others (Reference Capelli, Kapil, Reiweger, Or and Schweizer2016), obtained from acoustic wave propagation measurements. The observed differences are due to the fact that snow deformation is not purely elastic and also includes time dependent visco-plastic components, except for very fast loading rates and/or small deformations below the elastic limit. This is particularly true for experiments slower than the ductile-to-brittle transition of snow, which typically occurs for strain rates around 10−3 s−1 (e.g. Narita, Reference Narita1980; Schweizer, Reference Schweizer1998). Hence, quasi-static values represent an effective elastic modulus and most reported values include time dependent strain components.
$ \dot{\rm \varepsilon} \gt 10^{ - 2} \,{\rm s}^{ - 1} $
, and even higher values were reported by Capelli and others (Reference Capelli, Kapil, Reiweger, Or and Schweizer2016), obtained from acoustic wave propagation measurements. The observed differences are due to the fact that snow deformation is not purely elastic and also includes time dependent visco-plastic components, except for very fast loading rates and/or small deformations below the elastic limit. This is particularly true for experiments slower than the ductile-to-brittle transition of snow, which typically occurs for strain rates around 10−3 s−1 (e.g. Narita, Reference Narita1980; Schweizer, Reference Schweizer1998). Hence, quasi-static values represent an effective elastic modulus and most reported values include time dependent strain components.
With regard to weak layer specific fracture energy, far fewer measurements exist. Laboratory measurements are challenging due to the fragile nature of weak layers (Reiweger and Schweizer, Reference Reiweger and Schweizer2010, Reference Reiweger and Schweizer2013; Reiweger and others, Reference Reiweger, Gaume and Schweizer2015), and direct field measurements of the material properties of the snowpack are difficult and scarce (Föhn and others, Reference Föhn, Camponovo and Krüsi1998). Several studies introduced indirect methods to derive mechanical snow properties from field experiments. Sigrist and Schweizer (Reference Sigrist and Schweizer2007) were the first to estimate w f with field experiments and finite element (FE) modeling. Their method requires a Propagation Saw Test (PST; van Herwijnen and Jamieson, Reference van Herwijnen and Jamieson2005; Sigrist and Schweizer, Reference Sigrist and Schweizer2007; Gauthier and Jamieson, Reference Gauthier and Jamieson2008) to determine the critical cut length r c and a snow micro-penetrometer measurement (SMP; Schneebeli and Johnson, Reference Schneebeli and Johnson1998) to estimate the effective elastic modulus E of the slab. While Sigrist and Schweizer (Reference Sigrist and Schweizer2007) reported a mean fracture energy of 0.07 J m−2, more recent results using the same methodology on eight different weak layers indicate substantially larger values, typically around 1 J m–2 (Schweizer and others, Reference Schweizer, van Herwijnen and Reuter2011). Similar values (between 0.5 and 2 J m−2) were also found by Reuter and others (Reference Reuter, Proksch, Löwe, van Herwijnen and Schweizer2013) and Reuter and others (Reference Reuter, Schweizer and van Herwijnen2015) by integrating the penetration force signal of the SMP over the weak layer thickness. The differences in w f between Sigrist and Schweizer (Reference Sigrist and Schweizer2007) and Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011) arise from lower effective moduli used in the latter, obtained by using a more recent signal processing method for analyzing SMP force signals (Marshall and Johnson, Reference Marshall and Johnson2009; Löwe and van Herwijnen, Reference Löwe and van Herwijnen2012). The large differences in w f highlight the sensitivity of this approach to the method used to estimate the effective elastic modulus and the accuracy thereof. Unfortunately, the various procedures for determining the effective elastic modulus of snow lead to incompatible results and it remains unclear which method to use. A field-based experimental approach to determine the relevant mechanical properties of the snowpack seems most appropriate to resolve this discrepancy.
By extending the previously published methodological approach and data from van Herwijnen and Heierli (Reference van Herwijnen and Heierli2010), in this study, we report the effective elastic modulus of the slab and the specific fracture energy of the underlying weak layer for 80 different snowpack configurations. Using a video sequence of a PST, both parameters are estimated from the displacement field of the slab prior to crack propagation.
2. METHODS
2.1. Field experiments and particle tracking
We conducted 222 field experiments from 2008 to 2015 at 80 sites in Switzerland and in the USA. A PST (Gauthier and Jamieson, Reference Gauthier and Jamieson2008) modified to have slope normal, rather than vertical column ends was used in the field to measure critical crack lengths. A rectangular section of snow, 0.3 m across the slope and 0.9–3 m up the slope, was isolated on all sides. Starting from the down-slope end of the column, the weak layer was cut using a snow saw until crack propagation started. Numerous black markers were inserted in the snow above and below the weak layer. To scale the images, we measured the distance between the outermost markers in the top row. Experiments were recorded with a video camera with frame rates ranging from 15 to 480 frames s−1 (fps; Table 2). A 2 mm thick saw was used on harder slabs, while a 5 mm thick saw was used on very soft slabs to avoid crack-face contact. At each field site, a snow profile was recorded, giving information about grain shape and size, layer thickness, density and hand hardness index of snowpack layers.
A particle tracking velocimetry algorithm (PTV; Crocker and Grier, Reference Crocker and Grier1996) was used to analyze the displacement of the markers in a coordinate system aligned with the slope (Fig. 1). Displacements
![]() $u_x (r)$
and
$u_x (r)$
and
![]() $u_y (r)$
of each marker at cut length r were measured with reference to the initial positions x
0 and |y
0 | before cutting. The uncertainty in the position measurements was determined as the standard deviation of marker positions prior to sawing (overall mean 0.08 mm; range 0.01–0.4 mm). Saw cut lengths were estimated in 5–15 key frames, depending on the frame rate and length of the video recording. Key frames were evenly distributed from the start of the experiment to the onset of crack propagation. For frames in between the key frames, the saw cut length was estimated by linear interpolation. The critical cut length r
c was determined as the saw cut length in the last frame before crack propagation.
$u_y (r)$
of each marker at cut length r were measured with reference to the initial positions x
0 and |y
0 | before cutting. The uncertainty in the position measurements was determined as the standard deviation of marker positions prior to sawing (overall mean 0.08 mm; range 0.01–0.4 mm). Saw cut lengths were estimated in 5–15 key frames, depending on the frame rate and length of the video recording. Key frames were evenly distributed from the start of the experiment to the onset of crack propagation. For frames in between the key frames, the saw cut length was estimated by linear interpolation. The critical cut length r
c was determined as the saw cut length in the last frame before crack propagation.

Fig. 1. (a) Schematic representation of the experimental setup and coordinate system used in the analysis with x the slope parallel direction, y the slope normal direction and θ the slope angle. (b) FE model setup with a snow slab of total length L unsupported over the crack length r and rigidly supported at the base along the remaining length L–r. Triangles indicate fixed nodes.
Despite using a tripod, some unwanted camera movement was present in the majority of the experiments (88%). Post-processing was thus required to remove the resulting spurious displacements from the marker trajectories. Specifically, the average displacements
![]() $\overline {u_x (r)} $
and
$\overline {u_x (r)} $
and
![]() $\overline {u_y (r)} $
of markers at the up-slope end of the snow column were subtracted from the displacements of each marker (Fig. 2). The exact number and position of the markers used for averaging was determined by visual examination of marker trajectories on a case-by-case basis.
$\overline {u_y (r)} $
of markers at the up-slope end of the snow column were subtracted from the displacements of each marker (Fig. 2). The exact number and position of the markers used for averaging was determined by visual examination of marker trajectories on a case-by-case basis.
2.2. Derivation of mechanical properties
To determine the effective elastic modulus of the slab and the weak layer fracture energy from the displacement fields obtained from PST experiments, we used a method based on the work by Heierli and others (Reference Heierli, Gumbsch and Zaiser2008). For the test geometry shown in Figure 1, they suggested a formulation for the energy of an edge crack of length r. The total energy of the system
![]() $V(r) = V_{\rm f} (r) + V_{\rm m} (r)$
consists of the fracture energy
$V(r) = V_{\rm f} (r) + V_{\rm m} (r)$
consists of the fracture energy
![]() $V_{\rm f} (r)$
and the mechanical energy
$V_{\rm f} (r)$
and the mechanical energy
![]() $V_{\rm m} (r)$
. The fracture energy is the energy required to destroy the cohesion along the crack faces and is given by
$V_{\rm m} (r)$
. The fracture energy is the energy required to destroy the cohesion along the crack faces and is given by
![]() $V_{\rm f} (r) = w_{\rm f} r$
, with w
f the weak layer specific fracture energy per unit crack surface. The mechanical energy
$V_{\rm f} (r) = w_{\rm f} r$
, with w
f the weak layer specific fracture energy per unit crack surface. The mechanical energy
![]() $V_{\rm m} (r) = V_{\rm e} (r) + V_{\rm p} (r)$
consists of strain energy
$V_{\rm m} (r) = V_{\rm e} (r) + V_{\rm p} (r)$
consists of strain energy
![]() $V_{\rm e} (r)$
and gravitational potential energy
$V_{\rm e} (r)$
and gravitational potential energy
![]() $V_{\rm p} (r)$
and is the energy available for crack expansion.
$V_{\rm p} (r)$
and is the energy available for crack expansion.
To derive an expression for the mechanical energy
![]() $V_{\rm m} (r)$
, Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) assumed that changes in strain energy and gravitational potential energy of the slab are the main contributor to
$V_{\rm m} (r)$
, Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) assumed that changes in strain energy and gravitational potential energy of the slab are the main contributor to
![]() $V_{\rm m} (r)$
and contributions from the weak layer and substrate are negligible. Both the weak layer and the substrate are thus considered as rigid and
$V_{\rm m} (r)$
and contributions from the weak layer and substrate are negligible. Both the weak layer and the substrate are thus considered as rigid and
![]() $V_{\rm m} (r)$
can be described by two terms (see below)
$V_{\rm m} (r)$
can be described by two terms (see below)
where the load on the weak layer exerted by the slab of mean density ρ and thickness D consists of a negative shear stress τ = −ρgDsinθ and a negative compressive stress σ = −ρgDcosθ. Here,
![]() $E' = E/(1 - \nu ^2 )$
is the plane strain elastic modulus of the slab, assumed uniform, E is the elastic modulus, ν the Poisson's ratio (assumed = 0.2) and γ is a constant (assumed = 1; Heierli and others, Reference Heierli, Gumbsch and Zaiser2008). The terms in square brackets are given by
$E' = E/(1 - \nu ^2 )$
is the plane strain elastic modulus of the slab, assumed uniform, E is the elastic modulus, ν the Poisson's ratio (assumed = 0.2) and γ is a constant (assumed = 1; Heierli and others, Reference Heierli, Gumbsch and Zaiser2008). The terms in square brackets are given by
with
![]() $\eta = \sqrt {4(1 + \nu )/5} $
. The mechanical energy in Eqn (2) consists of two terms: a fracture mechanical and a bending term. The first term on the right-hand side is the fracture mechanical term and accounts for the elastic strain energy released by the material surrounding the crack when the crack advances. It is obtained by integrating the energy release rate G of a mixed/mode interface crack between two different elastic media over r (Eqn (2.29) in Hutchinson and Suo, Reference Hutchinson and Suo1992). The solution provided by Hutchinson and Suo (Reference Hutchinson and Suo1992) is valid for semi-infinite elastic media, thus only for short crack lengths (i.e. r < D). For longer crack lengths, bending of the unsupported part of the slab contributes considerable strain energy. The second term in Eqn (2), which is valid for longer cracks (i.e. r ≥ D), describes this contribution by considering the slab as a Timoshenko beam which is fixed to the rigid weak layer beyond the crack tip.
$\eta = \sqrt {4(1 + \nu )/5} $
. The mechanical energy in Eqn (2) consists of two terms: a fracture mechanical and a bending term. The first term on the right-hand side is the fracture mechanical term and accounts for the elastic strain energy released by the material surrounding the crack when the crack advances. It is obtained by integrating the energy release rate G of a mixed/mode interface crack between two different elastic media over r (Eqn (2.29) in Hutchinson and Suo, Reference Hutchinson and Suo1992). The solution provided by Hutchinson and Suo (Reference Hutchinson and Suo1992) is valid for semi-infinite elastic media, thus only for short crack lengths (i.e. r < D). For longer crack lengths, bending of the unsupported part of the slab contributes considerable strain energy. The second term in Eqn (2), which is valid for longer cracks (i.e. r ≥ D), describes this contribution by considering the slab as a Timoshenko beam which is fixed to the rigid weak layer beyond the crack tip.
The mechanical energy in Eqn (2) can be estimated from the measured displacement fields. Indeed, according to the theorem of Clapeyron, for a linear-elastic system,
![]() $V_{\rm m} = V_{\rm e} - V_{\rm p} = \displaystyle{1 \over 2}V_{\rm p} - V_{\rm p} = - \displaystyle{1 \over 2}V_{\rm p} $
, with V
e the strain energy stored in the body and V
p the gravitational potential energy. Snow slabs are rarely uniform, and in our experiments the slab above the weak layer generally consisted of several layers with different densities. The gravitational potential energy was therefore computed by dividing the slab into n layers, corresponding to the number of rows of markers in the slab (Fig. 1), of thickness D
i and density ρ
i. The mechanical energy is then computed as
$V_{\rm m} = V_{\rm e} - V_{\rm p} = \displaystyle{1 \over 2}V_{\rm p} - V_{\rm p} = - \displaystyle{1 \over 2}V_{\rm p} $
, with V
e the strain energy stored in the body and V
p the gravitational potential energy. Snow slabs are rarely uniform, and in our experiments the slab above the weak layer generally consisted of several layers with different densities. The gravitational potential energy was therefore computed by dividing the slab into n layers, corresponding to the number of rows of markers in the slab (Fig. 1), of thickness D
i and density ρ
i. The mechanical energy is then computed as
 $$V_{\rm m}^{PTV} (r) = - \displaystyle{1 \over 2}V_p (r) = - \displaystyle{1 \over 2}\sum\limits_{i = 1}^n \rho _i gD_i (\overline {u_{x,i} (r)} \sin \theta + \overline {u_{y,i} (r)} \cos \theta ),$$
$$V_{\rm m}^{PTV} (r) = - \displaystyle{1 \over 2}V_p (r) = - \displaystyle{1 \over 2}\sum\limits_{i = 1}^n \rho _i gD_i (\overline {u_{x,i} (r)} \sin \theta + \overline {u_{y,i} (r)} \cos \theta ),$$
with
![]() $\overline {u_{x,i} (r)} $
and
$\overline {u_{x,i} (r)} $
and
![]() $\overline {u_{y,i} (r)} $
the mean displacements of the markers in layer i. To account for slab stratigraphy, we therefore introduce an effective elastic modulus
$\overline {u_{y,i} (r)} $
the mean displacements of the markers in layer i. To account for slab stratigraphy, we therefore introduce an effective elastic modulus
![]() $E^{\rm \star} $
. It is defined as the modulus of a uniform slab of equal mean density and yielding the same displacement field as the real slab. To estimate
$E^{\rm \star} $
. It is defined as the modulus of a uniform slab of equal mean density and yielding the same displacement field as the real slab. To estimate
![]() $E^{\rm \star} $
, first E′ is determined for which Eqn (2) most accurately fits the mechanical energy derived by Eqn (6). Then, the relation
$E^{\rm \star} $
, first E′ is determined for which Eqn (2) most accurately fits the mechanical energy derived by Eqn (6). Then, the relation
![]() $E^{\rm \star} = (1 - \nu ^2 )E'$
is used to obtain the effective elastic modulus. Once E′ has been determined, the specific fracture energy is easily obtained by numerical differentiation of Eqn (2):
$E^{\rm \star} = (1 - \nu ^2 )E'$
is used to obtain the effective elastic modulus. Once E′ has been determined, the specific fracture energy is easily obtained by numerical differentiation of Eqn (2):
![]() $w_{\rm f} = G_{\rm c} = - \displaystyle{d \over {dr}}V_{\rm m} (r) \vert_{r = r_{\rm c}} $
. The described method can also be used to determine
$w_{\rm f} = G_{\rm c} = - \displaystyle{d \over {dr}}V_{\rm m} (r) \vert_{r = r_{\rm c}} $
. The described method can also be used to determine
![]() $E^{\rm \star} $
only by performing a PST in which there is no crack propagation, for instance when making the saw cut within a thick uniform snow layer and not in a weak layer.
$E^{\rm \star} $
only by performing a PST in which there is no crack propagation, for instance when making the saw cut within a thick uniform snow layer and not in a weak layer.
The uncertainties in the derived
![]() $E^{\rm \star} $
and w
f values were estimated using a Monte Carlo method to account for the PTV measurement uncertainty and uncertainties associated with the observations made in the field: density ±5%, scaling distance measurement ±1%, slope angle ±1°. By making 103 random draws from the probability distributions for the input quantities (assumed normal), the resulting distributions were evaluated. The values of
$E^{\rm \star} $
and w
f values were estimated using a Monte Carlo method to account for the PTV measurement uncertainty and uncertainties associated with the observations made in the field: density ±5%, scaling distance measurement ±1%, slope angle ±1°. By making 103 random draws from the probability distributions for the input quantities (assumed normal), the resulting distributions were evaluated. The values of
![]() $E^{\rm \star} $
and w
f reported here are the mean of the respective distributions. The reported uncertainty,
$E^{\rm \star} $
and w
f reported here are the mean of the respective distributions. The reported uncertainty,
![]() $\sigma _{{\rm E}^{\rm \star}} $
and
$\sigma _{{\rm E}^{\rm \star}} $
and
![]() $\sigma _{{\rm w}_{\rm f}} $
respectively, is twice the standard deviation of the respective distributions, which gives a level of confidence of approximately 95%.
$\sigma _{{\rm w}_{\rm f}} $
respectively, is twice the standard deviation of the respective distributions, which gives a level of confidence of approximately 95%.
2.3. FE simulations
The expression for the mechanical energy
![]() $V_{\rm m} (r)$
in Eqn (2) was derived based on empirical evidence. Indeed, Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) note that adding the fracture mechanical and the bending terms results in mechanical energy estimates that compare well with FE simulations. While Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) provided some supporting evidence to confirm their statement, a thorough validation is still required to investigate the reliability of Eqn (2) for a parameter range typically encountered in field experiments.
$V_{\rm m} (r)$
in Eqn (2) was derived based on empirical evidence. Indeed, Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) note that adding the fracture mechanical and the bending terms results in mechanical energy estimates that compare well with FE simulations. While Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) provided some supporting evidence to confirm their statement, a thorough validation is still required to investigate the reliability of Eqn (2) for a parameter range typically encountered in field experiments.
For this parametric study we used FE simulations to model the displacement of a snow slab bending over the edge of a rigid substrate, similar to the model setup employed by Reuter and others (Reference Reuter, Schweizer and van Herwijnen2015). In the model, a snow slab is rigidly supported at its base and unsupported along the crack length r (Fig. 1b). The slab has uniform material properties and is inclined at a slope angle θ. The same boundary conditions and model geometry were chosen as Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) described to derive Eqn (2). The model domain was divided into 2-D, quadrilateral plane strain elements with eight nodes each. The mesh consisted of 100 nodes m−1 in the vertical and horizontal direction, but node density was increased to 500 nodes m−1 in the unsupported section. The input parameters included slope angle, elastic modulus, Poisson's ratio (fixed value of 0.2), slab density, slab thickness, crack length and length of the beam (fixed at 10 m to avoid edge effects). The model system was loaded by gravity and solved in ANSYS workbench to obtain the total strain energy for a given crack length r. The FE simulation was run once for a system with a crack of size r, and once with a very short crack of r = 0.01 m. The difference in strain energy between these two states was termed
![]() $V_{\rm m}^{{\rm FEM}} (r)$
and compared with Eqn (2).
$V_{\rm m}^{{\rm FEM}} (r)$
and compared with Eqn (2).
3. RESULTS
3.1. Sensitivity study of Eqn (2)
We performed 120 FE simulations to investigate the influence of slab density ρ, slab thickness D, crack length r, elastic modulus E and slope angle θ on the accuracy of the mechanical energy computed with Eqn (2). Overall, numerically obtained
![]() $V_{\rm m}^{{\rm FEM}} (r)$
values were larger than those obtained with Eqn (2), up to a factor 2 (Fig. 3). While the elastic modulus and density of the slab did not influence the results (Figs 3a, b), slope angle and the ratio r/D substantially influenced the accuracy of Eqn (2) (Figs 3c, d). Indeed,
$V_{\rm m}^{{\rm FEM}} (r)$
values were larger than those obtained with Eqn (2), up to a factor 2 (Fig. 3). While the elastic modulus and density of the slab did not influence the results (Figs 3a, b), slope angle and the ratio r/D substantially influenced the accuracy of Eqn (2) (Figs 3c, d). Indeed,
![]() $V_{\rm m}^{{\rm FEM}} (r)/V_{\rm m} (r)$
increased with θ and decreased with r/D. There was also a weak influence of r, however only for very short crack lengths (Table 1; colors in Fig. 3d). Compared with the sensitivity to θ and r/D, the influence of r was deemed negligible.
$V_{\rm m}^{{\rm FEM}} (r)/V_{\rm m} (r)$
increased with θ and decreased with r/D. There was also a weak influence of r, however only for very short crack lengths (Table 1; colors in Fig. 3d). Compared with the sensitivity to θ and r/D, the influence of r was deemed negligible.

Fig. 2. Post-processing to remove spurious displacement due to camera movement. (a) Slope parallel displacement with time before correction. Colors indicate the vertical position y 0 of the markers relative to the weak layer. (b) Slope normal displacement with time before correction. Colors indicate the horizontal position x 0 of the markers relative to the right edge of the PST. (c) Displacement field at r = r c before correction. The black dashed square shows the markers that were used to calculate the mean displacement used for correcting marker trajectories. (d), (e) and (f) displacements after correction.

Fig. 3. Ratio (dots) between numerically obtained mechanical energy
![]() $V_{\rm m}^{FEM} (r)$
and
$V_{\rm m}^{FEM} (r)$
and
![]() $V_{\rm m} (r)$
obtained with Eqn (2) for various input parameters. A ratio of one (black dashed line) would mean perfect agreement. (a)
$V_{\rm m} (r)$
obtained with Eqn (2) for various input parameters. A ratio of one (black dashed line) would mean perfect agreement. (a)
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with elastic modulus E. (b)
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with elastic modulus E. (b)
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with density ρ. (c)
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with density ρ. (c)
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with slope angle θ. (d)
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with slope angle θ. (d)
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with the ratio between crack length r and slab thickness D. Colors indicate the crack length.
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with the ratio between crack length r and slab thickness D. Colors indicate the crack length.
To investigate the influence of θ and r/D in more detail, we carried out an additional 1430 FE simulations (Table 1; Fig. 4). Again,
![]() $V_{\rm m}^{{\rm FEM}} (r)$
values were larger than those obtained with Eqn (2), except for r/D < 0.05, a value recorded in only one field experiments. The influence of θ decreased with increasing r/D, in particular for r/D > 1, values encountered only in ~10% of our field experiments. Clearly, for realistic r/D values (Table 2; black dots in Fig. 4c), the sensitivity of the mechanical energy computed with Eqn (2) to θ and r/D has to be accounted for. To obtain more reliable effective elastic modulus estimates, we therefore used the adjusted mechanical energy
$V_{\rm m}^{{\rm FEM}} (r)$
values were larger than those obtained with Eqn (2), except for r/D < 0.05, a value recorded in only one field experiments. The influence of θ decreased with increasing r/D, in particular for r/D > 1, values encountered only in ~10% of our field experiments. Clearly, for realistic r/D values (Table 2; black dots in Fig. 4c), the sensitivity of the mechanical energy computed with Eqn (2) to θ and r/D has to be accounted for. To obtain more reliable effective elastic modulus estimates, we therefore used the adjusted mechanical energy
with
![]() $V_{\rm m} (r)$
the mechanical energy obtained with Eqn (2) and
$V_{\rm m} (r)$
the mechanical energy obtained with Eqn (2) and
![]() $Y(r/D,\theta )$
a correction factor that was extracted from a lookup table based on the FE simulations (Fig. 4c).
$Y(r/D,\theta )$
a correction factor that was extracted from a lookup table based on the FE simulations (Fig. 4c).

Fig. 4. (a) Ratio (dotted curves) between numerically obtained mechanical energy
![]() $V_{\rm m}^{FEM} (r)$
and
$V_{\rm m}^{FEM} (r)$
and
![]() $V_{\rm m} (r)$
obtained using Eqn (2) with slope angle θ. Colors indicate the ratio between crack length r and slab thickness D. (b)
$V_{\rm m} (r)$
obtained using Eqn (2) with slope angle θ. Colors indicate the ratio between crack length r and slab thickness D. (b)
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with r/D. Colors indicate θ. (c) Contour plot of
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with r/D. Colors indicate θ. (c) Contour plot of
![]() $V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with r/D and θ. The black dots represent the PST experiments.
$V_{\rm m}^{FEM} (r)/V_{\rm m} (r)$
with r/D and θ. The black dots represent the PST experiments.
Table 1. Overview of range of input parameters used in the FE simulations
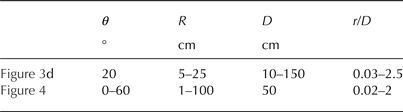
θ: slope angle; r: crack length; D: slab thickness; r/D: ratio between crack length and slab thickness.
3.2. Measured displacement fields
Displacement fields were analyzed in 222 PSTs at 80 sites covering a wide range of slab and weak layer properties (Tables 2 and 3). The observed displacement fields were characteristic of slab bending in several aspects (Fig. 5). First, the displacement in the unsupported part of the slab steadily increased with increasing r (Figs 5a, b before 2.8 s). Second, slope-normal displacement
![]() $u_y (x_0, y_0 )$
was independent of |y
0 | (Fig. 5c) and decreased with increasing x
0 (Fig. 5b). Third, slope-parallel displacement
$u_y (x_0, y_0 )$
was independent of |y
0 | (Fig. 5c) and decreased with increasing x
0 (Fig. 5b). Third, slope-parallel displacement
![]() $u_x (x_0, y_0 )$
was very close to zero or positive (upslope) immediately above the weak layer
$u_x (x_0, y_0 )$
was very close to zero or positive (upslope) immediately above the weak layer
![]() $(y_0 = 0)$
and negative (downslope) close to the snow surface (Fig. 5a). For x
0 >r
c, the displacement decreased with x
0 (Fig. 5c). On average, at the critical cut length r
c, u
y decreased from ~0.6 mm at x
0 = 0 to ~0.2 mm at x
0 = r
c and vanished near x
0 = 2r
c (black curve in Fig. 6). In other words, there was slope normal displacement beyond the crack tip, typically up to a distance of 2r
c. The displacements of the markers in the substrate were indistinguishable from the background noise (Figs 2f and 5c) indicating that the substrate does not notably deform during a PST.
$(y_0 = 0)$
and negative (downslope) close to the snow surface (Fig. 5a). For x
0 >r
c, the displacement decreased with x
0 (Fig. 5c). On average, at the critical cut length r
c, u
y decreased from ~0.6 mm at x
0 = 0 to ~0.2 mm at x
0 = r
c and vanished near x
0 = 2r
c (black curve in Fig. 6). In other words, there was slope normal displacement beyond the crack tip, typically up to a distance of 2r
c. The displacements of the markers in the substrate were indistinguishable from the background noise (Figs 2f and 5c) indicating that the substrate does not notably deform during a PST.

Fig. 5. Displacement measurements for a PST performed on a weak layer consisting of rounding faceted particles with θ = 19°, D = 36 cm,
![]() $\rho _{slab} = 226\, {\rm kg} {\rm m}^{ - 3} $
and
$\rho _{slab} = 226\, {\rm kg} {\rm m}^{ - 3} $
and
![]() $r_{\rm c} = 20\, {\rm cm}$
. (a) Negative slope parallel displacement with time. Colors indicate the vertical position |y
0 | of the markers relative to the weak layer. (b) Slope normal displacement with time. Colors indicate the horizontal position x
0 of the markers relative to the right edge of the PST. The insets represent a zoom of the bending phase before the onset of crack propagation. (c) Displacement field at r = r
c. The direction of gravity is indicated with the arrow, which, for scale, is 20 cm long.
$r_{\rm c} = 20\, {\rm cm}$
. (a) Negative slope parallel displacement with time. Colors indicate the vertical position |y
0 | of the markers relative to the weak layer. (b) Slope normal displacement with time. Colors indicate the horizontal position x
0 of the markers relative to the right edge of the PST. The insets represent a zoom of the bending phase before the onset of crack propagation. (c) Displacement field at r = r
c. The direction of gravity is indicated with the arrow, which, for scale, is 20 cm long.

Fig. 6. Slope normal displacement u y with normalized distance x 0/r c for all 222 tests (each color represent one test) at the critical cut length r = r c, i.e. the onset of crack propagation. The mean slope normal displacement of all experiments is depicted by the thick black curve.
Table 2. Overview of range of experimental parameters, effective elastic modulus of the slab
![]() $E^{\rm \star} $
and weak layer specific fracture energy w
f. fps: frame rate of the recordings; θ: slope angle; ρ: average slab density; D: slope normal slab thickness; r
c: mean critical cut length
$E^{\rm \star} $
and weak layer specific fracture energy w
f. fps: frame rate of the recordings; θ: slope angle; ρ: average slab density; D: slope normal slab thickness; r
c: mean critical cut length

Table 3. Percentage of tested weak layers by grain type, according to Fierz and others (Reference Fierz2009)

PP, precipitation particles; DF, decomposing and fragmented precipitation particles; RG, rounded grains; FC, faceted crystals; FCxr, rounding faceted particles; DH, depth hoar; SH, surface hoar.
It has been suggested that time dependent deformation of the snow slab needs to be accounted for in PSTs (e.g. McClung, Reference McClung2009). In order to investigate this issue, the time-dependency of test results was examined by performing 52 side-by-side PST experiments on a weak layer of depth hoar on 15 February 2010. In half these experiments the cut speed was fast (<1 s to r c), while in the other experiments the cut speed was slow (>30 s to r c). There was no significant difference in r c for fast cut speeds (r c = 26 ± 6 cm) and slow cut speeds (r c = 24 ± 7 cm; T-test p = 0.22).
3.3. Derived mechanical properties
The largest observed slope normal displacements prior to crack propagation were generally on the order of 1 mm or less (Fig. 6). In comparison, the mean uncertainty of the position measurements by the PTV method was 0.08 mm. Considerable scatter in the derived mechanical energy was therefore present, as seen in Figure 7 for the experiment shown in Figure 5. Nevertheless, the trend in
![]() $V_{\rm m}^* (r)$
was clear and generally well described by Eqns (2) and (7). For the example shown in Figure 7, the normalized root-mean-squared error (NRMSE; normalized with
$V_{\rm m}^* (r)$
was clear and generally well described by Eqns (2) and (7). For the example shown in Figure 7, the normalized root-mean-squared error (NRMSE; normalized with
![]() $V_{\rm m}^{PTV} (r = r_{\rm c} )$
) was 12%. Overall, the NRMSE ranged from 4 to 38% with a mean of 15% and significantly decreased with increasing r/D ratio (Spearman r = 0.29, p < 0.01).
$V_{\rm m}^{PTV} (r = r_{\rm c} )$
) was 12%. Overall, the NRMSE ranged from 4 to 38% with a mean of 15% and significantly decreased with increasing r/D ratio (Spearman r = 0.29, p < 0.01).

Fig. 7. Derived mechanical energy with crack length r for the experiment shown in Figure 5. The red dots represent the key frames at which the saw cut length r was estimated from the images. The black line represents the best fit of
![]() $V_{\rm m}^* (r)$
(Eqn (7)) to the experimental data
$V_{\rm m}^* (r)$
(Eqn (7)) to the experimental data
![]() $V_{\rm m}^{{\rm PTV}} (r)$
(Eqn (6), blue dots), and the black dashed-dotted lines the 95% confidence interval. The green dashed line represents the tangent to the mechanical energy at
$V_{\rm m}^{{\rm PTV}} (r)$
(Eqn (6), blue dots), and the black dashed-dotted lines the 95% confidence interval. The green dashed line represents the tangent to the mechanical energy at
![]() $r = r_{\rm c} = 0.2\, {\rm m}$
.
$r = r_{\rm c} = 0.2\, {\rm m}$
.
Overall, we estimated
![]() $E^{\rm \star} $
in 222 PSTs and it ranged from 0.08 to 34 MPa with a median of 3 MPa (Table 2). We estimated w
f in 206 PSTs and it ranged from 0.08 to 2.7 J m−2 with a median of 0.4 J m−2. The mean uncertainty in the derived
$E^{\rm \star} $
in 222 PSTs and it ranged from 0.08 to 34 MPa with a median of 3 MPa (Table 2). We estimated w
f in 206 PSTs and it ranged from 0.08 to 2.7 J m−2 with a median of 0.4 J m−2. The mean uncertainty in the derived
![]() $E^{\rm \star} $
values was ~25% (range from 20 to 67%), and the mean uncertainty in w
f was 16% (range from 6 to 50%). In about half of the experiments, the crack propagated to the end of the snow sample (106 of 222 experiments), while in the remaining experiments fracture arrest was observed. Interestingly,
$E^{\rm \star} $
values was ~25% (range from 20 to 67%), and the mean uncertainty in w
f was 16% (range from 6 to 50%). In about half of the experiments, the crack propagated to the end of the snow sample (106 of 222 experiments), while in the remaining experiments fracture arrest was observed. Interestingly,
![]() $E^{\rm \star} $
was significantly lower for experiments in which cracks arrested (median 2.1 MPa) than for experiments in which the crack propagated to the very end (median 3.6 MPa; U-test p < 0.01), in line with recent experimental and numerical results (Birkeland and van Herwijnen, Reference Birkeland and van Herwijnen2014; Schweizer and others, Reference Schweizer, Reuter, van Herwijnen, Jamieson and Gauthier2014). In contrast, w
f was similar in cases of fracture arrest (median 0.44 J m−2) and in cases where the crack propagated (median 0.42 J m−2).
$E^{\rm \star} $
was significantly lower for experiments in which cracks arrested (median 2.1 MPa) than for experiments in which the crack propagated to the very end (median 3.6 MPa; U-test p < 0.01), in line with recent experimental and numerical results (Birkeland and van Herwijnen, Reference Birkeland and van Herwijnen2014; Schweizer and others, Reference Schweizer, Reuter, van Herwijnen, Jamieson and Gauthier2014). In contrast, w
f was similar in cases of fracture arrest (median 0.44 J m−2) and in cases where the crack propagated (median 0.42 J m−2).
In general,
![]() $E^{\rm \star} $
correlated well with mean slab density (Spearman r = 0.69, p < 0.01; Fig. 8). A reasonable fit to the experimental data (NRMSE of 13%; blue dashed curve in Fig. 8) was given by the empirical power law,
$E^{\rm \star} $
correlated well with mean slab density (Spearman r = 0.69, p < 0.01; Fig. 8). A reasonable fit to the experimental data (NRMSE of 13%; blue dashed curve in Fig. 8) was given by the empirical power law,

Fig. 8. Effective elastic modulus
![]() $E^{\rm \star} $
with slab density. Field data (blue dots) and power law fit (blue dashed curve). Also shown are the parameterizations from laboratory studies presented in Scapozza (Reference Scapozza2004) (green line), Camponovo and Schweizer (Reference Camponovo and Schweizer2001) (red line) and Sigrist (Reference Sigrist2006) (black line) as well as estimates from SMP measurements (squares) from Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011).
$E^{\rm \star} $
with slab density. Field data (blue dots) and power law fit (blue dashed curve). Also shown are the parameterizations from laboratory studies presented in Scapozza (Reference Scapozza2004) (green line), Camponovo and Schweizer (Reference Camponovo and Schweizer2001) (red line) and Sigrist (Reference Sigrist2006) (black line) as well as estimates from SMP measurements (squares) from Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011).
Most of our measurements fell between the empirical model reported by Scapozza (Reference Scapozza2004) based on laboratory measurements on 200 uniform snow samples (green line in Fig. 8), and the model reported by Camponovo and Schweizer (Reference Camponovo and Schweizer2001) based on laboratory measurements performed at 1 Hz (red line in Fig. 8). However, the model reported by Sigrist (Reference Sigrist2006) based on cyclic loading experiments at 100 Hz (black line in Fig. 8) resulted in larger
![]() $E^{\rm \star} $
values than almost all of our measurements.
$E^{\rm \star} $
values than almost all of our measurements.
There was a weak negative correlation between weak layer specific fracture energy w
f and slope angle (Spearman r = −0.2, p < 0.01). On the other hand, w
f significantly correlated with the total overlying stress
![]() $\sigma _0 = \sqrt {\tau ^2 + \sigma ^2} = \rho gD$
(Spearman r = 0.51, p < 0.01; Fig. 9b). Finally, w
f values showed some dependence on grain type (Fig. 9a). While most of the investigated weak layers consisted of persistent grains (FC, FCxr, DH and SH in Table 3), there were also six weak layers of precipitation particles (PP) and 7 layers of decomposed and fragmented precipitation particles or rounded grains (DF/RG). The median weak layer specific fracture energy was highest for DF/RG and DH, while the lowest values of w
f were associated with PP.
$\sigma _0 = \sqrt {\tau ^2 + \sigma ^2} = \rho gD$
(Spearman r = 0.51, p < 0.01; Fig. 9b). Finally, w
f values showed some dependence on grain type (Fig. 9a). While most of the investigated weak layers consisted of persistent grains (FC, FCxr, DH and SH in Table 3), there were also six weak layers of precipitation particles (PP) and 7 layers of decomposed and fragmented precipitation particles or rounded grains (DF/RG). The median weak layer specific fracture energy was highest for DF/RG and DH, while the lowest values of w
f were associated with PP.

Fig. 9. (a) Weak layer specific fracture energy by grain type. On each box, the central line is the median, the edges of the box are the 1st and 3rd quartiles, the whiskers extend to the most extreme data points. (b) Weak layer specific fracture energy vs total overlying stress σ 0 = ρgD.
3.4. Reproducibility
At 53 sites, more than one PST was performed. To investigate the reliability of the measurements, we therefore determined the mean measurement uncertainty for each site, defined as
![]() $\overline {\sigma _{\rm E}} = \sqrt {\displaystyle{1 \over n}\Sigma _{i = 1}^n \sigma _{{\rm E}^{\rm *}, i}^2} $
and
$\overline {\sigma _{\rm E}} = \sqrt {\displaystyle{1 \over n}\Sigma _{i = 1}^n \sigma _{{\rm E}^{\rm *}, i}^2} $
and
![]() $\overline {\sigma _{{\rm w}_{\rm f}}} = \sqrt {\displaystyle{1 \over n}\Sigma _{i = 1}^n \sigma _{{\rm w}_{\rm f}, i}^2} $
, with n the number of measurements at the site. We also determined the uncertainty in the mean
$\overline {\sigma _{{\rm w}_{\rm f}}} = \sqrt {\displaystyle{1 \over n}\Sigma _{i = 1}^n \sigma _{{\rm w}_{\rm f}, i}^2} $
, with n the number of measurements at the site. We also determined the uncertainty in the mean
![]() $\Delta E^{\rm \star} $
and Δw
f for each site, defined as
$\Delta E^{\rm \star} $
and Δw
f for each site, defined as
![]() $R/2\sqrt n $
where the range R is the difference between the maximum and the minimum values of
$R/2\sqrt n $
where the range R is the difference between the maximum and the minimum values of
![]() $E^{\rm \star} $
and w
f, respectively. If the uncertainty in the mean was >1.25 times the mean uncertainty, we considered the measurement not reproducible. At 92% (49 out of 53) of the sites with more than one PST,
$E^{\rm \star} $
and w
f, respectively. If the uncertainty in the mean was >1.25 times the mean uncertainty, we considered the measurement not reproducible. At 92% (49 out of 53) of the sites with more than one PST,
![]() $\Delta E^{\rm \star} \le 1.25\overline {\sigma _{{\rm E}^{\rm \star}}} $
, suggesting very good reproducibility of the obtained
$\Delta E^{\rm \star} \le 1.25\overline {\sigma _{{\rm E}^{\rm \star}}} $
, suggesting very good reproducibility of the obtained
![]() $E^{\rm \star} $
values in nearby locations. The reproducibility for w
f was substantially poorer, since at only 46% (22 out of 48) of the sites
$E^{\rm \star} $
values in nearby locations. The reproducibility for w
f was substantially poorer, since at only 46% (22 out of 48) of the sites
![]() $\Delta w_{\rm f} \le 1.25\overline {\sigma _{{\rm w}_{\rm f}}} $
(blue dots in Fig. 10).
$\Delta w_{\rm f} \le 1.25\overline {\sigma _{{\rm w}_{\rm f}}} $
(blue dots in Fig. 10).

Fig. 10. (a) Uncertainty in the mean effective elastic modulus
![]() $E^{\rm \star} $
with mean measurement uncertainty at sites with more than one PST. The black line shows the one-to-one relation. Red dots show sites where the uncertainty in the mean was larger than 1.25 the mean measurement uncertainty. (b) Same as in (a) for the weak layer specific fracture energy w
f.
$E^{\rm \star} $
with mean measurement uncertainty at sites with more than one PST. The black line shows the one-to-one relation. Red dots show sites where the uncertainty in the mean was larger than 1.25 the mean measurement uncertainty. (b) Same as in (a) for the weak layer specific fracture energy w
f.
4. DISCUSSION
A recently developed method was applied to determine the weak layer specific fracture energy w
f and the effective elastic modulus of the overlying snow slab
![]() $E^{\rm \star} $
from 222 field experiments at 80 sites by considering slab bending in a PST (van Herwijnen and Heierli, Reference van Herwijnen and Heierli2010). By cutting with a snow saw into the weak layer below the slab, the unsupported part of the slab bends and the corresponding displacement field prior to the onset of crack propagation was analyzed using particle tracking velocimetry. From changes in the mechanical energy with increasing crack length we estimated an effective elastic modulus of the slab and weak layer specific fracture energy based on an analytical expression (Heierli and others, Reference Heierli, Gumbsch and Zaiser2008).
$E^{\rm \star} $
from 222 field experiments at 80 sites by considering slab bending in a PST (van Herwijnen and Heierli, Reference van Herwijnen and Heierli2010). By cutting with a snow saw into the weak layer below the slab, the unsupported part of the slab bends and the corresponding displacement field prior to the onset of crack propagation was analyzed using particle tracking velocimetry. From changes in the mechanical energy with increasing crack length we estimated an effective elastic modulus of the slab and weak layer specific fracture energy based on an analytical expression (Heierli and others, Reference Heierli, Gumbsch and Zaiser2008).
To assess the accuracy of this analytical expression, we conducted a parametric study using FE simulations. Results showed that the analytical energy formulation is most accurate for long cracks, i.e. r ≫ D, and is sensitive to slope angle θ and r/D. The strong sensitivity to r/D was somewhat expected, since the bending term in Eqn (2) becomes dominant for r ≫ D. However, for typical values found in the field experiments, i.e. r ≤ D and 0° ≤ θ ≤ 45°, a correction factor was thus required to obtain an adjusted mechanical energy in line with the FE simulations (Eqn (7) and Figure 4).
A number of assumptions were made to derive the expression for the mechanical energy provided by Heierli and others (Reference Heierli, Gumbsch and Zaiser2008), in particular (1) brittle fracture, (2) linear elastic behavior of the slab and (3) a rigid substrate. This first assumption relates to the weak layer failure mechanism, which is not clearly defined. It is important to point out that the exact failure mechanism, in terms of defining a failure envelope for the weak layer, is not needed here since the energy required to advance the crack per unit area is given by w f, regardless of the failure mechanism. Nevertheless, the fracture is assumed to occur under mixed mode loading and since it is brittle, negligible plastic deformation is assumed to take place prior to fracture. It has been argued that snow is a quasi-brittle material (e.g. Bažant and others, Reference Bažant, Zi and McClung2003; McClung, Reference McClung2009), and the existence of a finite fracture process zone around the crack tip, in which plastic deformation takes place, has to be accounted for. However, for critical crack lengths typically encountered in field experiments, Gaume and others (Reference Gaume2014) recently showed that both approaches lead to very comparable results.
The latter two assumptions, namely linear elastic behavior of the slab and a rigid substrate, were required to derive an expression for the mechanical energy with crack length r (Eqn (2)). The principal underlying assumption here is that changes in strain energy and gravitational potential energy of the slab are the main contributors to the overall energy of the system and are much larger than the contributions from the weak layer and the substrate. Our measurements show that the displacement in the snowpack layers below the weak layer was indistinguishable from the background noise (Figs 2f and 5c). Furthermore, the observed displacement fields clearly show slab bending prior to crack propagation, suggesting that substantial potential energy is available for crack propagation. While it is clear that we cannot confirm which part of the displacement observed in the experiments is associated with recoverable (elastic) deformation, overall our results suggest that the assumptions made to derive the expression for the mechanical energy seem valid, at the very least as a first approximation. Thus, applying the theory of Heierli and others (Reference Heierli, Gumbsch and Zaiser2008) to analyze our experimental data is appropriate to obtain first order estimates of
![]() $E^{\rm \star} $
and w
f from in-situ field tests.
$E^{\rm \star} $
and w
f from in-situ field tests.
Regarding the determination of the effective elastic modulus of the slab, various experimental procedures exist to determine
![]() $E^{\rm \star} $
values. Depending on the experimental procedure, mainly the applied loading or deformation rate, differences by a factor of 10 or more are possible (e.g. Camponovo and Schweizer, Reference Camponovo and Schweizer2001; Scapozza, Reference Scapozza2004; Sigrist and Schweizer, Reference Sigrist and Schweizer2007; Marshall and Johnson, Reference Marshall and Johnson2009). In our field tests, the effective elastic modulus of the slab ranged from 0.08 to 34 MPa with a median of 3 MPa, similar to values reported by Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011), who estimated
$E^{\rm \star} $
values. Depending on the experimental procedure, mainly the applied loading or deformation rate, differences by a factor of 10 or more are possible (e.g. Camponovo and Schweizer, Reference Camponovo and Schweizer2001; Scapozza, Reference Scapozza2004; Sigrist and Schweizer, Reference Sigrist and Schweizer2007; Marshall and Johnson, Reference Marshall and Johnson2009). In our field tests, the effective elastic modulus of the slab ranged from 0.08 to 34 MPa with a median of 3 MPa, similar to values reported by Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011), who estimated
![]() $E^{\rm \star} $
values from snow micro-penetrometer measurements (squares in Fig. 8). The observed increase in
$E^{\rm \star} $
values from snow micro-penetrometer measurements (squares in Fig. 8). The observed increase in
![]() $E^{\rm \star} $
with slab density ranged between the empirical model of Scapozza (Reference Scapozza2004) and that of Camponovo and Schweizer (Reference Camponovo and Schweizer2001), whereas the model used by Sigrist and Schweizer (Reference Sigrist and Schweizer2007) predicts much higher elastic moduli (Fig. 8). The experiments conducted by Scapozza (Reference Scapozza2004) and Camponovo and Schweizer (Reference Camponovo and Schweizer2001) were performed at low strain rates
$E^{\rm \star} $
with slab density ranged between the empirical model of Scapozza (Reference Scapozza2004) and that of Camponovo and Schweizer (Reference Camponovo and Schweizer2001), whereas the model used by Sigrist and Schweizer (Reference Sigrist and Schweizer2007) predicts much higher elastic moduli (Fig. 8). The experiments conducted by Scapozza (Reference Scapozza2004) and Camponovo and Schweizer (Reference Camponovo and Schweizer2001) were performed at low strain rates
![]() $(\dot{\rm \varepsilon} \lt 10^{ - 3} \,{\rm s}^{ - 1} )$
, whereas Sigrist and Schweizer (Reference Sigrist and Schweizer2007) reported values obtained with a dynamic method at 100 Hz. For the field experiments, the strain rate can roughly be approximated as
$(\dot{\rm \varepsilon} \lt 10^{ - 3} \,{\rm s}^{ - 1} )$
, whereas Sigrist and Schweizer (Reference Sigrist and Schweizer2007) reported values obtained with a dynamic method at 100 Hz. For the field experiments, the strain rate can roughly be approximated as
![]() $\dot{\rm \varepsilon} = (u_{{\rm y,max}} /r_c \Delta t)$
, with u
y,max the maximum observed slope normal displacement at r = r
c and Δt the time required to reach the critical crack length. In our field test,
$\dot{\rm \varepsilon} = (u_{{\rm y,max}} /r_c \Delta t)$
, with u
y,max the maximum observed slope normal displacement at r = r
c and Δt the time required to reach the critical crack length. In our field test,
![]() $\dot{\rm \varepsilon} $
ranged from 6 × 10−5 s−1 to 2 × 10−2 s−1 with a mean of 10−3 s−1, in line with the range of
$\dot{\rm \varepsilon} $
ranged from 6 × 10−5 s−1 to 2 × 10−2 s−1 with a mean of 10−3 s−1, in line with the range of
![]() $E^{\rm \star} $
values obtained. Results from side-by-side PST experiments with fast and slow cut speeds showed no significant differences. Nevertheless, it seems likely that given the low strain rates involved in PSTs, time-dependent strain components contribute to slab bending. Furthermore, possible plastic effects in the slab during bending, for instance local bond-breaking events, might also be present. At present, both time-dependent and plastic effects are not accounted for in the model.
$E^{\rm \star} $
values obtained. Results from side-by-side PST experiments with fast and slow cut speeds showed no significant differences. Nevertheless, it seems likely that given the low strain rates involved in PSTs, time-dependent strain components contribute to slab bending. Furthermore, possible plastic effects in the slab during bending, for instance local bond-breaking events, might also be present. At present, both time-dependent and plastic effects are not accounted for in the model.
Regarding the determination of the specific fracture energy of the weak layer, our w f values had a median value of 0.4 J m−2. The w f data exhibited a significant dependence on total overlying stress, suggesting that w f increases with increasing overburden. This comes as no surprise since additional load and time causes densification and pressure sintering, resulting in increased bonding (e.g. Brown and others, Reference Brown, Satyawali, Lehning and Bartelt2001; Szabo and Schneebeli, Reference Szabo and Schneebeli2007; Podolskiy and others, Reference Podolskiy2014). Similarly, Jamieson and Johnston (Reference Jamieson and Johnston2001), Zeidler and Jamieson (Reference Zeidler and Jamieson2006) and van Herwijnen and Miller (Reference van Herwijnen and Miller2013) reported a significant positive correlation between strength, overlying load and burial time for persistent and nonpersistent weak layers. Finally, our results also suggest that the lowest w f values are generally associated with precipitation particles (Fig. 9), which is in line with the fact that these weak layers are generally very recent.
Overall, the values of the specific fracture energy are in line with recently published results by van Herwijnen and Heierli (Reference van Herwijnen and Heierli2010), Schweizer and others (Reference Schweizer, van Herwijnen and Reuter2011) and Reuter and others (Reference Reuter, Proksch, Löwe, van Herwijnen and Schweizer2013) which ranged from 0.4 to 2.2 J m−2. On the other hand, our w
f values are almost an order of magnitude larger than the first reported field measurement of 0.07 J m−2 by Sigrist and Schweizer (Reference Sigrist and Schweizer2007), or estimates from avalanche crown faces ranging from 0.001 to 0.2 J m−2 reported by McClung (Reference McClung2007) assuming simple shear fracture as fracture mechanism for slab avalanche release. These important discrepancies arise from sensitivities of these previously reported w
f values to
![]() $E^{\rm \star} $
estimates. To circumvent this problem, McClung (Reference McClung2015) recently used the cohesive crack model to estimate w
f values from avalanche crown faces (0.08–0.36 J m−2) and PST experiments (0.04–0.1 J m−2). While
$E^{\rm \star} $
estimates. To circumvent this problem, McClung (Reference McClung2015) recently used the cohesive crack model to estimate w
f values from avalanche crown faces (0.08–0.36 J m−2) and PST experiments (0.04–0.1 J m−2). While
![]() $E^{\rm \star} $
estimates are not required in the cohesive crack model, the total slip at failure and the size of the fracture process zone are required, both of which cannot be measured in the field. In contrast, with the method employed here, both w
f and
$E^{\rm \star} $
estimates are not required in the cohesive crack model, the total slip at failure and the size of the fracture process zone are required, both of which cannot be measured in the field. In contrast, with the method employed here, both w
f and
![]() $E^{\rm \star} $
are obtained directly for the measured displacement field and are independent of each other since their values are determined simultaneously from the adjusted mechanical energy function (Eqn (7)).
$E^{\rm \star} $
are obtained directly for the measured displacement field and are independent of each other since their values are determined simultaneously from the adjusted mechanical energy function (Eqn (7)).
Recently, LeBaron and Miller (Reference LeBaron and Miller2014) used a microstructural model based on X-ray computer tomography to estimate w f, yielding values ranging between 0.005 and 0.05 J m−2. In their work, the specific fracture energy was calculated by determining the energy required for breaking the bonds in the minimum cut area i.e. the path most prone to fracture. Their model thus assumed that bonds outside the minimum energy fracture path do not break. However, plastic effects outside the minimum energy path also play a role in the fracture process and should influence w f. In our approach, the assumption is made that all the energy associated with the observed deformation is available for crack propagation. Thus, any energy dissipation due to nonelastic deformation (viscous and plastic) is neglected, leading to high w f values. Hence, our weak layer specific fracture energy values also represent effective values, including all energy sinks (elastic and plastic) in the system (LeBaron and Miller, Reference LeBaron and Miller2014). Clearly, the high w f values we obtained compared with typical values for ice (~0.5–2 J m−2) suggest that a substantial fraction of the potential energy may not be available to drive crack expansion but is otherwise dissipated. In addition, displacements in the slab were found, even for x 0 >r c (Fig. 6) suggesting that deformation might also occur inside the weak layer and the substratum. Therefore, future work taking into account time dependent and nonlinear plastic effects in the slab as well as the mechanical properties of the weak layer and the substratum may extend the results under discussion here. Furthermore, the assumption that the mechanical energy is equal to half the work of gravity is not valid any more when nonelastic parts of deformation are included into the work function.
The measurements of the displacement field allows evaluation of the guidelines for performing a PST. Based on a statistical analysis of numerous field tests, Gauthier and Jamieson (Reference Gauthier and Jamieson2008) recommended that the length of a PST should be at least 1 m, while the critical cut length should not exceed half the column length. Since the snow slab typically deformed up to a distance of 2r c (Fig. 6), the latter recommendation is insufficient. To remove the influence of the free upslope end of the column, we suggest that the column should be sufficiently long to ensure that the critical cut length does not exceed one third of the column length. This is in line with results from Bair and others (Reference Bair, Simenhois, van Herwijnen and Birkeland2014) who used FE modeling to show that edge effects occur when r c is larger than one fifth of the column length. For typical r c values of ~30 cm, this translates to a recommended column length of at least 150 cm. Note, however, that for studying dynamic crack propagation, even longer snow samples are required (van Herwijnen and others, Reference van Herwijnen, Schweizer and Heierli2010; Bair and others, Reference Bair, Simenhois, van Herwijnen and Birkeland2014; Gaume and others, Reference Gaume, van Herwijnen, Schweizer, Chambon and Birkeland2015).
The approach outlined in this paper provides a method to derive mechanical snow properties from field measurements. The consistency of results obtained in side-by-side experiments (Fig. 10) indicates that the method can be used to reliably determine the effective elastic modulus
![]() $E^{\rm \star} $
. However, poorer reproducibility was found for the weak layer specific fracture energy w
f due to error propagation when taking the derivative of the mechanical energy. An advantage of our method is that the effective elastic modulus can be measured on snow samples in the field, including low density snow (<150 kg m−3) and that w
f and
$E^{\rm \star} $
. However, poorer reproducibility was found for the weak layer specific fracture energy w
f due to error propagation when taking the derivative of the mechanical energy. An advantage of our method is that the effective elastic modulus can be measured on snow samples in the field, including low density snow (<150 kg m−3) and that w
f and
![]() $E^{\rm \star} $
as well as other fracture mechanical properties such as collapse height, propagation speed and crack-face friction, can be extracted from the same field data (van Herwijnen and Jamieson, Reference van Herwijnen and Jamieson2005; van Herwijnen and Heierli, Reference van Herwijnen and Heierli2009; van Herwijnen and others, Reference van Herwijnen and Heierli2010; Bair and others, Reference Bair, Simenhois, Birkeland and Dozier2012).
$E^{\rm \star} $
as well as other fracture mechanical properties such as collapse height, propagation speed and crack-face friction, can be extracted from the same field data (van Herwijnen and Jamieson, Reference van Herwijnen and Jamieson2005; van Herwijnen and Heierli, Reference van Herwijnen and Heierli2009; van Herwijnen and others, Reference van Herwijnen and Heierli2010; Bair and others, Reference Bair, Simenhois, Birkeland and Dozier2012).
5. CONCLUSION
We evaluated both the slab effective elastic modulus and the weak layer specific fracture energy from a single field experiment. Artificial cracks were induced in the weak layer using a saw, which caused bending of the slab prior to crack propagation. The method consists of analyzing the resulting displacement field in the slab using particle tracking velocimetry. Then the mechanical energy of the system is computed from the measured displacement field and fitted to an adjusted analytical expression allowing the determination of the effective elastic modulus of the slab and the weak layer specific fracture energy. We present these essential snow properties for 80 different snowpack configurations including persistent as well as nonpersistent weak layers. The effective elastic modulus ranged from 0.08 to 34 MPa and increased with mean slab density according to a power law relationship. The weak layer specific fracture energy ranged from 0.08 to 2.7 J m−2 and increased with increasing load. An analysis of the measurement uncertainties highlighted the robustness of the effective elastic modulus estimates but also showed a poorer reproducibility of obtained weak layer specific fracture energy values.
In the future, accounting for visco-plastic effects in the slab and in the weak layer will be required to refine the presented results and relax the stringent assumptions of the model, namely the purely elastic behavior of the slab and the rigid character of the weak layer and the substrate.
ACKNOWLEDGEMENTS
We acknowledge the contribution of Joachim Heierli. Furthermore, we would like to thank Sascha Bellaire, Achille Capelli, Stephan Harvey, Matthias Heck, Susanna Mitterer, Christoph Mitterer, Ron Simenhois, Stephan Simioni and Franziska Zahner for assistance with field work. Finally, we are grateful for the comments by three anonymous reviewers that helped to improve the manuscript.















