1. Introduction
Both the magnitude and spatial distribution of changes in freshwater flux from the Greenland ice sheet are likely to have implications across a spectrum of spatial and temporal scales. On an ocean basin scale, the freshwater flux into the North Atlantic Ocean exerts a strong control on the meridional overturning circulation, which plays a major role in global climate (Reference StoufferStouffer and others, 2006). Changes in Greenland’s freshwater flux can affect sea-ice formation in neighboring ocean basins, in turn influencing the air–sea exchange (Reference Gelderloos, Straneo and KatsmanGelderloos and others, 2012) and marine ecosystems (Reference Greene, Pershing, Cronin and CeciGreene and others, 2008) across the region. On the scale of individual glacial fjords, changes in the magnitude and spatial distribution of freshwater flux can influence fjord stratification and circulation by promoting a stable stratified water column or driving exchange with the neighboring shelf (Reference StraneoStraneo and others, 2011). Enhanced exchange of warming shelf waters may, in turn, influence the dynamic behavior of Greenland’s marine-terminating glaciers by modifying submarine melt rates or destabilizing ice-front melange (Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and MotykaAmundson and others, 2010; Reference Howat, Box, Ahn, Herrington and McFaddenHowat and others, 2010).
The freshwater flux from the Greenland ice sheet into adjacent ocean basins has increased rapidly over the past two decades due to enhanced surface meltwater runoff from the ablation zone and intensified iceberg discharge from marine-terminating glaciers in the southeast and northwest (Reference Van den BroekeVan den Broeke and others, 2009; Reference SasgenSasgen and others, 2012; Reference Enderlin, Howat, Jeong, Noh, Van Angelen and Van den BroekeEnderlin and others, 2014). For Greenland’s major drainage basins, changes in both iceberg discharge and surface meltwater runoff were asynchronous and spatially variable (Reference Van den BroekeVan den Broeke and others, 2009; Reference SasgenSasgen and others, 2012), resulting in order-of-magnitude cumulative freshwater flux anomaly differences from neighboring ocean basins (Reference Bamber, Van den Broeke, Ettema, Lenaerts and RignotBamber and others, 2012). It is likely that the distribution of freshwater fluxes also varies within each ocean basin depending on the relative contribution of iceberg discharge and surface meltwater runoff. For ocean basins where changes in freshwater flux can primarily be explained by interannual variability in surface meltwater runoff, the freshwater flux from the ice sheet is concentrated at glacier grounding lines (i.e. as a point source in each fjord). In contrast, melting of drifting icebergs acts as a spatially distributed source of fresh water to the fjord–shelf systems.
Freshwater fluxes from surface meltwater runoff and iceberg melting have not been well characterized or quantified for Greenland’s glacial fjords, largely due to challenges in obtaining hydrographic observations near the margins of actively calving glaciers and in iceberg-congested waters. For the few glacial fjords in Greenland with hydrographic observations, a cold and fresh surface layer is usually present (Reference StraneoStraneo and others, 2012) and likely varies with the availability of terrestrial runoff, surface meltwater runoff and/or iceberg meltwater. The runoff terms can be estimated for a glacial fjord using temperature and precipitation observations from local meteorological stations or from climate reanalysis models (e.g. Reference Bamber, Van den Broeke, Ettema, Lenaerts and RignotBamber and others, 2012) but submarine meltwater contributions are more challenging to estimate. Simple model parameterizations can be used if hydrographic observations are available (e.g. Reference Bigg, Wadley, Stevens and JohnsonBigg and others (1997) for icebergs and Reference Motyka, Hunter, Echelmeyer and ConnorMotyka and others (2003) for a glacier terminus), although the underlying assumptions required to estimate submarine melting from hydrography may not be valid for all glacial fjords (Suther-land and Reference StraneoStraneo, 2012). Most models assume a two-layer estuarine circulation inland of available hydrographic data (e.g. Reference Motyka, Hunter, Echelmeyer and ConnorMotyka and others, 2003; Reference Rignot, Koppes and VelicognaRignot and others, 2010), but detailed observations in Sermilik Fjord show that stratification of the ambient water masses and entrainment of a subglacial meltwater plume originating at several hundred meters depth can create multiple residual circulation cells, which complicate the estuarine-like circulation (Sutherland and Reference StraneoStraneo, 2012). Here we describe an alternative data-driven approach using changes in the iceberg surface elevation (i.e. freeboard) to estimate submarine melt rates.
Changes in iceberg freeboard are derived by differencing repeat digital elevation models (DEMs) extracted from very high-resolution stereo imagery collected by the WorldView-1 and –2 satellites. The DEM differencing technique has been widely used to map thickness and volume changes of Greenland’s marine-terminating outlet glaciers (Reference Stearns and HamiltonStearns and Hamilton, 2007; Reference Howat, Smith, Joughin and ScambosHowat and others, 2008; Reference McFadden, Howat, Joughin, Smith and AhnMcFadden and others, 2011; Reference Walsh, Howat, Ahn and EnderlinWalsh and others, 2012) from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) stereo image pairs. ASTER images are not well suited for studying iceberg elevation changes, however, because (1) their relatively coarse (15 m)-resolution pixels cannot adequately resolve icebergs, and (2) the several-meter vertical uncertainty of ASTER DEMs (e.g. Reference Stearns and HamiltonStearns and Hamilton, 2007) likely exceeds the difference in iceberg freeboard between DEM acquisition dates. With the recent launch of the WorldView series of very high-resolution stereo imaging satellites, it has become possible to observe subtle elevation changes for relatively small objects such as icebergs. Here we derive iceberg melt rates by differencing WorldView DEMs, which have both higher spatial resolution (~1.65 m) and lower vertical uncertainty (σ = 2.9 m) than ASTER products used for glaciological studies. To demonstrate our method and quantify potential sources of uncertainty, we carry out an analysis of submarine melt-water fluxes and rates for icebergs in Sermilik Fjord, East Greenland.
2. Data And Methodology
2.1. Stereo imagery
We use panchromatic imagery collected by the WorldView-1 and –2 satellites over Sermilik Fjord during the 2011–13 boreal summers. Two factors drive our selection of ideal image pairs. First, the time separation between DEMs needs to be long enough that measurable changes in iceberg surface elevations exceed sources of measurement error. Second, icebergs that break free of the near-terminus melange are capable of drifting up to 8 km d–1 (Reference Roth, Sutherland, Hamilton and StearnsRoth and others, 2013), meaning they can exit the region of interest if the time between images is too long. The selected images have a mean horizontal resolution of 0.55 m and a repeat interval of ~3–46 days (Table 1; Fig. 1). Cloud cover is negligible (i.e. covering < 1% of the image) in 15 of the 16 image pairs used herein (the image acquired on 24 August 2011 contains partially transparent clouds), enabling the construction of DEMs from all of the selected stereo images using the methods described below.
Table 1. Estimated submarine melt freshwater flux and associated uncertainty for all tracked icebergs in the 2011–13 high-resolution WorldView DEMs of Sermilik Fjord. The freshwater flux is 0.9 times the ice equivalent volume flux


Fig. 1. WorldView DEM footprints overlaid on a 2005 RADARSAT mosaic. Coordinates are in Polar Stereo, with a standard Parallel of 70° N and central Meridian of 45° W. DEM dates are distinguished by line color and style (see legend). The line colors distinguish the DEM pairs used in our analysis, with solid lines indicating the initial DEMs, and dashed lines indicating repeat DEMs. The primary iceberg sources are Helheim (HG) and Midgard (MG) glaciers.
2.2. DEM construction and co-registration
DEMs are generated using the NASA Ames Stereo Pipeline (ASP) software package (http://ti.arc.nasa.gov/tech/asr/intelligent-robotics/ngt/stereo/), an open-source suite of automated geodesy and stereogrammetry tools designed for processing planetary imagery. Extracting DEMs from ~0.5 m resolution stereo images is computationally intensive. To reduce processing time, we implement a parallelized version of ASP on the University of Maine high-performance supercomputing cluster, and only construct DEMs for image pairs containing large and distinctly shaped icebergs that can be visually identified on multiple acquisition dates.
DEM processing involves three steps: map projection, point cloud construction and DEM generation. A brief description of the ASP workflow is given below; additional details are described in the ASP User’s Guide.
The first task is to re-project the raw stereo images onto a low-resolution hole-less DEM with the ASP mapproject command. This step is optional, but has the advantage of decreasing the overall computation time. Here we use the Greenland Ice Mapping Project (GIMP) DEM (http://bprc.osu.edu/GDG/gimpdem.php) (Reference Howat, Negrete and SmithHowat and others, 2014) as our low-resolution hole-less DEM. Next, ASP uses a series of cross-correlation algorithms to generate a disparity map (i.e. a map of parallax between matched pixels) from the map-projected stereo images. The disparity map is used to generate a three-dimensional point cloud, which is converted to a DEM with the ASP point2dem command. The output DEM is automatically georeferenced using the satellite ephemeris metadata from the input stereo images. The point2dem command automatically produces an output DEM with the same post spacing (i.e. pixel resolution) as the input images, but we down-sample each DEM by a factor of three (average pixel size of 1.65 m) because the cross-correlation algorithms used in DEM construction are unlikely to successfully match all individual pixels within the image pairs (Intelligent Robotics Group, 2013). Down-sampling is carried out using a linear distance-weighted algorithm similar to the velocity down-sampling procedure described by Reference O’Neel, Pfeffer, Krimmel and MeierO’Neel and others (2005).
Derived differences in iceberg freeboard are due to (1) elevation bias between DEMs, (2) tidal height change between image acquisition times, (3) surface and submarine melting, and (4) random error in DEM elevations. We remove the bias between DEMs introduced by (1) and (2) by co-registering the DEM elevations within the fjord using two independent techniques. For each iceberg identified in the repeat DEMs, we first calculate the combined offset from (1) and (2) as the difference in the mean elevation of ice-free pixels adjacent to the iceberg (i.e. sea level) in the initial and subsequent DEMs. The difference in local sea level is then applied as a uniform adjustment to remove fjord elevation bias between DEMs. If consecutive DEMs contain overlapping bedrock regions, we also estimate the elevation bias between DEMs as the sum of the median difference in bedrock elevations and the change in the tidal height between image acquisition times. The difference in bedrock elevations is measured directly from the DEMs, and tidal height change is estimated using the Arctic Ocean Tidal Inverse Model (AOTIM-5) (Reference Padman and ErofeevaPadman and Erofeeva, 2004) for a site at the mouth of Sermilik Fjord. A location on the East Greenland continental shelf is used to estimate tidal height change because the tidal model is not expected to perform reliably inside a narrow fjord. However, previous work by Reference De JuanDe Juan and others (2010) shows no significant difference in phase and amplitude between predicted tides at the mouth of Sermilik Fjord from AOTIM-5 and tides observed at the head of the fjord using a water pressure sensor, giving us confidence that the AOTIM-5 derived tides are a reliable estimate for tidal height change in the vicinity of the surveyed icebergs.
Each bias-estimator technique has its advantages and disadvantages. Spatial variations in bias are effectively removed using the sea-level adjustment technique because the bias is estimated locally at each iceberg. In contrast, the bedrock- and tide-adjustment technique inherently assumes that the offset in bedrock elevations is uniform across the DEMs and that changes in tidal height are spatially invariant along the section of Sermilik Fjord contained in the DEMs. The sea-level adjustment technique can also be applied to all identified icebergs whereas the bedrock- and tide-adjustment technique can only be applied to DEMs with overlapping bedrock regions. The primary disadvantage of the sea-level adjustment technique is its dependence on local ice-free pixels, which are often difficult to identify in the dense ice melange located close to the terminus of Helheim Glacier.
2.3. Iceberg tracking
It is necessary to identify the same icebergs in successive images prior to differencing the DEMs. We manually track icebergs by visual inspection of each image and validate the identifications by visually comparing iceberg elevations in the DEMs. Automated feature-tracking techniques work well for deriving glacier flow speeds where motion is generally in a linear direction (e.g. Reference Howat, Ahn, Joughin, Van den Broeke, Lenaerts and SmithHowat and others, 2011), but are less well suited for tracking icebergs because their motion has more degrees of freedom (i.e. translation in multiple directions and rotation).
To ensure that elevations are extracted from the same iceberg area in all DEMs, we delineate the boundaries of each iceberg in its initial DEM using a polygon that excludes the pixels located within ~10 m of the iceberg margins (Fig. 2). We exclude the steeply sloped marginal pixels because we find that elevation uncertainties are larger over steep relief regions, as discussed below. A similar slope dependency has been observed in DEM-differencing analyses of glacier elevation change (e.g. Reference Howat, Smith, Joughin and ScambosHowat and others, 2008). We then manually shift and rotate the polygon within subsequent DEMs until it overlaps the same iceberg area as in the initial DEM. This operator-defined iceberg-tracking procedure is repeated ten times for each iceberg, minimizing the potential bias introduced by operator error.

Fig. 2. Example iceberg DEMs from (left) 24 June 2012 and (right) 29 June 2012. The area from which iceberg freeboard observations were extracted is delineated by the dashed black-and-white polylines. Elevations are distinguished by color (color bar). Dark-blue regions within the icebergs are data gaps, which are excluded from the DEM-differencing analysis. Within the melange, as shown here, the large icebergs (warm colors), bergy bits (light blues) and sea ice are separated horizontally by meters or less.
2.4. Estimating volume change
For each iceberg, we extract the freeboard for all pixels within the area bounded by the polygon in each of the co-registered DEMs and compute the pixel-by-pixel difference, dh, between the initial and repeat DEMs. We use the pixel-by-pixel freeboard differences for all ten iterations to compute the mean, dhμ , and standard deviation, dhσ . Next, we remove all freeboard difference values that exceed dhμ ± 3dhσ (three-sigma filter) and recompute the mean difference for the filtered observations. The mean freeboard change can then be converted to an estimate of mean thickness change, dHμ , by assuming the icebergs are fully floating and in hydrostatic equilibrium with the ocean water. For a fully floating iceberg, the ice thickness, H, and freeboard, h, are related by ρsw(H – h) = ρih, where ρsw and ρi are the ocean water and ice densities, respectively. The assumption of hydrostatic equilibrium is justified here for two reasons. First, we have observed seafloor depths of ~800 m in expendable conductivity, temperature and depth (XCTD) casts carried out in the inner fjord (unpublished data). For Helheim Glacier, the maximum keel depth (i.e. draft) of icebergs calved from the ~800 m thick terminus (Reference Enderlin, Howat, Jeong, Noh, Van Angelen and Van den BroekeEnderlin and others, 2014) is unlikely to exceed ~700 m, as supported by draft estimates for the analyzed icebergs, and iceberg shoaling should be uncommon. Second, for the icebergs analyzed herein, temporally averaged iceberg speeds ranged from tens of m d–1 (in the melange) to km d–1, suggesting that the icebergs were fully mobile during our observation periods.
The volume change, dV (m3 ice eq.), is calculated as
where A surf is the mean surface area of the iceberg face measured in the repeat stereo images (m2), ρ sw is the mean ocean water density (1026 kg m–3) and ρ i is the mean ice density (900 kg m–3). Ocean water density was derived from repeat hydrographic (XCTD and CTD) surveys within Sermilik Fjord (Reference StraneoStraneo and others, 2011; Sutherland and Reference StraneoStraneo, 2012). We choose a mean ice density slightly below the density of bubble-free ice (917 kg m–3) to account for void spaces in the icebergs inherited from the highly crevassed Helheim Glacier. Volume change can also be found from
where n and m are the number of pixels in the entire iceberg area at times t 1 and t 2, respectively, but this method requires that DEM errors are random. We find that although the DEM errors show a normal distribution over bedrock (see Section 2.5), very large elevation outliers (i.e. elevation spikes or holes) are present in areas of steep relief, particularly near the iceberg margins, potentially biasing volume change estimates calculated using Eqn (2). Therefore, we apply a three-sigma filter to our pixel-by-pixel elevation differences to remove any potential bias introduced by DEM blunders and calculate volume change using Eqn (1).
The derived change in the iceberg volume using Eqn (1) is the combination of surface and submarine melting between image acquisition dates. We estimate the surface melting component using a positive degree-day approach (Braith-waite, 1995) whereby daily surface melting is a function of summed air temperatures above 0°C. For Sermilik Fjord, surface air temperatures were obtained from a meteorological station adjacent to the terminus of Helheim Glacier (http://glacierresearch.org/locations/helheim/data.html) and adjusted to sea level using the June lapse rate of 4.7°C km–1 from Reference Fausto, Ahlstrøm, Van As, Bøggild and JohnsenFausto and others (2009). The adjusted mean daily temperatures are multiplied by a degree-day factor of 9 mm d–1 °C–1 to estimate daily surface melting (m) at the iceberg surface (Reference Fausto, Ahlstrøm, Van As, Bøggild and JohnsenFausto and others, 2009; Reference BoxBox, 2013). The degree-day parameterization was developed for land-based ice sheets and has not been tested for icebergs in a maritime environment, but in the absence of direct surface ablation measurements, we assume that it adequately estimates surface melting over the typically short observation periods considered here. Multiplying the surface melt rate by iceberg surface area (A surf) yields the volume loss due to surface ablation. The cumulative volume loss from surface melt is subtracted from the estimated dV, and the residual volume change is converted to freshwater equivalents (0.9dV residual), then divided by the time between acquisition dates to determine the freshwater flux (dV /dt) from submarine melting (Table 1).
2.5. Error analysis
Uncertainty in the submarine melt estimates consists of systematic and spatially random errors. Standard error propagation techniques are used to determine the effect of each component.
Systematic errors arise from uncertainty in (1) the DEM co-registration adjustment, (2) the ice and ocean water densities in Eqn (1), (3) the degree-day factor used to estimate surface melting, and (4) the iceberg surface area. We assess the potential bias associated with the DEM co-registration adjustment using freeboard change observations from the 24–29 June 2012 DEMs. This time period contains the largest number of iceberg volume change estimates (ten) in our dataset. We compare the freeboard changes derived from the local sea-level-adjusted DEMs to those derived from the bedrock- and tide-adjusted DEMs and find a median difference of ~0.04 m. Ocean water density exhibits small variability on the order of ±2 kg m–3, based on repeat hydrographic observations in Sermilik Fjord (Reference StraneoStraneo and others, 2011; Reference Sutherland and StraneoSutherland and Straneo, 2012). Iceberg density can potentially increase by up to ~20 kg m–3 between acquisition dates if any remaining void space becomes filled by meltwater. We assume that the degree-day factor can vary by ±2 mm d–1 °C–1 based on the Greenland surface air temperature analysis presented in Reference Fausto, Ahlstrøm, Van As, Bøggild and JohnsenFausto and others (2009). The surface area of each iceberg is manually measured in the initial and repeat satellite images, and the uncertainty is defined as the temporal range about the mean. Temporal changes in the measured surface area can be due to iceberg fragmentation, which increases with the time separation between DEM dates, operator uncertainty in distinguishing iceberg boundaries, and/or iceberg tilt in response to non-uniform volume change. On average, surface area uncertainty accounts for 27% of the volume flux uncertainty, with the highest relative contribution (56%) for the longest observation period (~46 days).
Random errors in the estimates of submarine melt volume flux are due to (1) DEM blunders and (2) uncertainty in the operator-defined iceberg tracking. Here we present random errors as one standard deviation. DEM blunders are the result of poor correlation between stereo images, likely due to the presence of shadows or clouds, or incorrect gain settings during image acquisition. Preliminary analysis of differences in the adjusted bedrock elevations in Sermilik Fjord suggests that the elevation uncertainty introduced by DEM blunders follows a normal distribution, with a standard deviation of hσ = 2.9 m. Although the magnitude of the DEM uncertainty likely varies between the bedrock and fjord due to differences in surface slope, texture, and contrast, we assume that the DEM uncertainty in the fjord will also follow an approximately normal distribution. As such, for the large icebergs (>3000 pixels) analyzed herein, this random uncertainty term decreases rapidly, accounting for an average of ~12% of the total volume flux uncertainty. Variations in surface texture over time and between icebergs cause the uncertainty in the operator-defined iceberg-tracking process to vary from iceberg to iceberg. We independently quantify this term as the standard deviation of the ten mean freeboard change measurements performed for each iceberg. The same operator tracked the icebergs in sequential images, so inter-operator biases are avoided. On average, manual iceberg tracking (i.e. translation and rotation) accounts for ~57% of the volume flux uncertainty.
3. Discussion
The remainder of our discussion focuses on freshwater fluxes (Table 1) and area-averaged submarine melt rates (m d–1) (Table 2) derived from the local sea-level-adjusted DEMs. Volume fluxes calculated with the bedrock- and tide-adjusted DEMs were spatially incoherent, with negative volume fluxes (implying ice accretion) obtained for three of the ten icebergs analyzed during the 24–29 June 2012 observation period. We attribute these physically implausible results to spatial variations in fjord elevations that are not adequately removed by the uniform bedrock- and tide adjustment, including variations in tidal height within the fjord and striping within the DEMs. As such, we exclude the volume flux estimates derived from the bedrock- and tide-adjusted DEMs from further analysis and assume that the DEM co-registration uncertainty for the local sea-level-adjusted DEMs is approximately zero. The local sea-level-adjusted freshwater flux and associated uncertainty (random error plus bias) estimates are listed in Table 1.
Table 2. Area-averaged melt rates assuming cylindrical or conical shapes below the waterline

To facilitate comparison of our results with other estimates of submarine melting, we convert the submarine melt volume flux for each iceberg to a melt rate per unit of submerged area (m d–1). The submerged volume, V sub, is calculated as
Where
Submerged surface area cannot be extracted from the repeat DEMs because the shape of V sub that can produce the observed freeboard values is non-unique. Instead, we estimate the submerged surface area of each iceberg using two idealized shapes: cylinders (subscript ‘cyl’) and cones (subscript ‘cone’) (Fig. 3). The mean perimeter measured for each iceberg in the initial and repeat stereo images, p surf, is used to define the surface radius of each idealized shape, r surf, as

Fig. 3. Illustration of the non-unique potential submerged geometries for a hypothetical iceberg and the idealized cylindrical and conical shapes used to estimate the submerged surface area. Labeled variables are described in the text accompanying Eqns (1–7). Note: iceberg freeboard and draft are not to scale.
By defining the idealized surface area with the measured iceberg perimeter, irregular iceberg shapes are taken into account in our idealized shapes. We do not consider a third possible shape, a truncated inverted cone (i.e. skirted iceberg), because the close proximity of icebergs in the melange (Fig. 2) suggests that the iceberg perimeter does not substantially increase below the waterline for the majority of the icebergs considered herein. The maximum keel depth (i.e. draft), d, for each shape is calculated as

and the submerged surface area, A sub, is calculated as
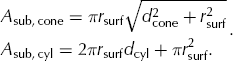
The submarine melt rate is then calculated as the ice equivalent volume flux divided by the submerged surface area, yielding an area-averaged melt rate for each iceberg. Surface roughness (i.e. small-scale variations in geometry) is not taken into account in our idealized shapes, so the melt rates presented in Table 2 should be considered upper-bound estimates.
The average melt rate for the idealized shapes is ~0.39 m d–1 (0.38 ± 0.17 m d–1 and 0.41 ± 0.18 m d–1 for cylinders and cones, respectively), which is considerably smaller than Helheim Glacier’s area-averaged melt rate at the terminus, ~1.8 m d–1 (650 m a–1), derived from synoptic hydrographic measurements collected in Sermilik Fjord in summer 2009 (Reference Sutherland and StraneoSutherland and Straneo, 2012). The difference in submarine melt rates between icebergs and the glacier terminus is not surprising given that both observations (Reference Motyka, Dryer, Amundson, Truffer and FahnestockMotyka and others, 2013) and numerical models (Reference Xu, Rignot, Menemenlis and KoppesXu and others, 2012) show that submarine melt rates increase with the strength of a rising meltwater plume. At a tidewater glacier terminus, subglacial discharge during the melt season drives vigorous plume convection, which entrains warm subsurface ocean water and potentially enhances submarine melting. Melt rates beneath relatively large, deep-keeled icebergs should be comparable to the melt rate for a glacier terminus in the same fjord in the absence of subglacial discharge, such as during winter. However, model simulations suggest that winter melt rates along the glacier terminus may still exceed melt rates beneath small icebergs, or bergy bits, because the deeper draft of the grounded glacier terminus provides a larger contact area over which rising meltwater can entrain warm ocean water, in turn enhancing meltwater convection and promoting higher maximum melt rates near the surface of the water mass (Reference Sciascia, Straneo, Cenedese and HeimbachSciascia and others, 2013). We find a weak relationship (R 2 = 0.53) between melt rates and iceberg draft for our 24–29 June 2012 data (not shown) and a mean iceberg melt rate of ~144 m a–1 (138 ± 61 m a–1 and 149 ± 67 m a–1 for cylinders and cones, respectively), which is in relatively good agreement with the winter melt rate of ~70 m a–1 simulated for Helheim Glacier using March 2010 hydrographic data and zero subglacial discharge (Reference Sciascia, Straneo, Cenedese and HeimbachSciascia and others, 2013). Intra- and interannual differences in the temperature, salinity, velocity and stratification of water masses within the fjord will also influence iceberg and glacier melt rates (Reference Sciascia, Straneo, Cenedese and HeimbachSciascia and others, 2013) and may partially explain the difference between our observed iceberg melt rates and the simulated glacier melt rate. Spatio-temporal variations in water mass properties and their effects on iceberg melting are topics of further investigation.
Despite the relatively low iceberg melt rates observed in Sermilik Fjord, the freshwater flux from submarine melting of icebergs may constitute a substantial fraction of the total freshwater flux to some glacial fjords. As shown in Figures 4 and 5, the iceberg freshwater flux varies with the surface area (Fig. 4; R 2 = 0.64) and the submerged area estimated using the idealized iceberg shapes (Fig. 5; R 2 ≥ 0.78). Deviations from the best-fit linear polynomials (dashed lines) may be due to a number of factors whose influence cannot be quantified with the available data, including small- (i.e. roughness) to large-scale (i.e. cylindrical vs conical) differences between the idealized and actual iceberg shapes, spatio-temporal variations in the temperature, salinity and velocity of the water mass(es) in which the icebergs are submerged, temporal variations in iceberg surface area, and differences in surface melting between icebergs not captured by the spatially uniform degree-day parameterization. Although all of these factors will likely influence the freshwater flux (and melt rate) for an individual iceberg, the strong relationships between iceberg shape and freshwater flux in our dataset suggest that fjords with expansive ice melange, such as Sermilik Fjord, will likely have large freshwater fluxes arising from iceberg submarine melting. For example, the ten icebergs studied between 24 and 29 June 2012 contributed a cumulative freshwater flux of ~2.5 × 10–5 Sv (1 Sv = 106 m3 s–1) to the fjord. To put this flux in perspective, we estimate that these icebergs make up 5% of the surface area of the ice melange visible in the 24 June 2012 image and represent just ~0.4 Gt of the ~32 Gt of ice discharged into Sermilik Fjord each year (Reference Enderlin, Howat, Jeong, Noh, Van Angelen and Van den BroekeEnderlin and others, 2014). The estimated mean summer surface meltwater flux for the Helheim Glacier catchment is ~1.7 × 10–4 Sv (Reference AndersenAndersen and others, 2010), which suggests that the iceberg freshwater flux likely constitutes >10% of the total freshwater flux delivered to the fjord during the summer months.

Fig. 4. Submarine melt freshwater flux vs mean surface area for the analyzed icebergs in Sermilik Fjord. Horizontal error bars indicate the temporal range in measured iceberg surface area. Vertical error bars indicate uncertainty associated with the freshwater flux estimates (see Section 2.5). Symbol colors correspond to the text colors of the dates in the legend. The dashed cyan and black lines are the best-fit linear polynomials for the 24–29 June 2012 data and the entire dataset, respectively. R 2 values for the best-fit polynomials are provided as a goodness-of-fit metric.

Fig. 5. Submarine melt freshwater flux vs mean submerged area for idealized (left) cylindrical and (right) conical iceberg shapes. Horizontal error bars indicate the temporal range in estimated submerged area. Vertical error bars indicate uncertainty associated with the freshwater flux estimates (see Section 2.5). Symbol colors correspond to the text colors of the dates in the Figure 4 legend. As in Figure 4, the dashed cyan and black lines are the best-fit linear polynomials for the 24–29 June 2012 data and the entire dataset, respectively, and the R 2 values for the best-fit polynomials are provided as a goodness-of-fit metric.
The relationship between submarine melting freshwater flux and submerged iceberg area also suggests that an increase in the submerged iceberg surface area in a fjord, which might follow a change in glacier discharge (e.g. Reference Enderlin, Howat, Jeong, Noh, Van Angelen and Van den BroekeEnderlin and others, 2014) or a change in glacier calving style (full-thickness tabular vs smaller sub-thickness icebergs) (e.g. Reference Schild and HamiltonSchild and Hamilton, 2013), will likely result in a change in the magnitude of the distributed freshwater flux from submarine melting of icebergs. Using the DEM-differencing approach described here, we may be able to quantify spatial and temporal changes in freshwater fluxes in the absence of detailed hydrographic surveys. In order to develop an improved understanding of the controls of iceberg freshwater flux and melt rate variability, however, we suggest that future research efforts focus on pairing hydrographic observations and remotely sensed iceberg observations with laboratory experiments and numerical modeling simulations of glacial fjords.
4. Conclusions
We show that submarine meltwater fluxes and melt rates for icebergs can be estimated by differencing repeat high-resolution DEMs, avoiding the need to perform logistically challenging, expensive and hazardous hydrographic surveys near active glacier margins. Uncertainties associated with iceberg freshwater flux and submarine melt rate estimates obtained using this method are well constrained, and relatively small as long as DEMs are vertically adjusted (i.e. co-registered) independently for each iceberg using local ice-free pixels. Our results for Sermilik Fjord reveal a mean summer iceberg melt rate of ~0.39 m d–1, ~80% smaller than inferred summer submarine melt rates along the vertical calving terminus of nearby Helheim Glacier. Iceberg melt rates are, instead, consistent with the simulated winter melt rate along the glacier terminus, which implies that the excess melting along the terminus in summertime is driven by subglacial discharge. We find that the distributed freshwater flux from melting icebergs may constitute a substantial fraction of the total freshwater flux to glacial fjords with high concentrations of icebergs and/or expansive ice melange. The relationships between the submarine melt volume flux and the surface and submerged iceberg areas suggest that the freshwater flux from icebergs should vary spatially and temporally with the glacier calving flux and style. Additional work is required to test whether these relationships hold for different fjord systems.
Acknowledgements
This work was supported by NASA award NNX13AK88G. WorldView images were distributed by the Polar Geospatial Center at the University of Minnesota (http://www.pgc.umn.edu/imagery/satellite/) as part of an agreement between the US National Science Foundation and the US National Geospatial Intelligence Agency Commercial Imagery Program. The background RADARSAT image in Figure 1 is courtesy of I. Joughin, University of Washington Applied Physics Lab. We thank Tim Bartholomaus and an anonymous reviewer for constructive comments that helped improve the quality of the manuscript, and Fiamma Straneo and Claudia Cenedese for insightful discussions on glacial fjord oceanography.









