Introduction
The intention of this paper is to examine the typical topographic features of avalanche terrain, and discuss whether terrain parameters only may be used for the calculation of extreme avalanche run–out distance. Determination of the different constants in (he well–known equations (Voellmy, 1955):

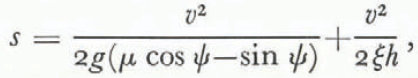
could then be avoided. The parameters ξ, relative terrain roughness, μ, coefficient of friction, and h, avalanche height, may vary between wide limits and consequently give different answers for velocity Ʋ and run–out distance, s (Perla, in press, and unpublished lectures in mechanics and hydrodynamics related to snow avalanches given in 1978—79 by B. Schieldrop). The exact calculation of maximum run–out distance for a given avalanche is not possible by any method. It therefore seems that a probabilistic approach to this problem may be the right way to go, whether one uses a pure hydrodynamical model, or an empirical model based on terrain parameters.
1. Field observations and data
1.1. Basis of avalanche registration
This study is based on a detailed registration and measurements of 850 avalanches (Lied, unpublished [a]; Haug, unpublished; Hestnes, unpublished). The majority of these avalanches occur in populated areas, where the local population have had knowledge of the avalanche behaviour and run–out areas for more than a hundred years. This is essential in such an investigation because it is impossible to base an identification of maximum run–out on damage to vegetation or geomorphological traces like transport and accumulation of loose deposits, as described by Reference Bovis and MearsBovis and Mears (1976), when the frequency of avalanches near their maximum extent may be of the order of 1 per 100 years or lower.
The knowledge of the maximum distance reached in each avalanche path is therefore based on interviews with the local population and the study of documents from local history, church documents, and old police reports describing avalanche damage.
Each avalanche is plotted on a map, scale 1 : 5000, contour interval 5 m, and scale 1 : 50000, contour interval 20 m, in its known maximum extent. The track and rupture zones are identified by air photograph interpretation and in the field.
A great number of the avalanches terminate in fjords or lakes. These are excluded from the study since maximum extent cannot be identified, and so are avalanches that bump into terrain obstacles like river banks and mounds in the run–out zones. Only avalanches with a free outlet in the valley bottom, arc therefore analysed here. This leaves 423 avalanches where terrain conditions and knowledge of observed maximum extent are good enough to be used. Finally III avalanches are treated by regression analysis based on data from the avalanche paths.
1.2. Topographic parameters used
All the avalanches studied have been known to the local population for more than a hundred years and for many avalanches there are documents which date back to the seventeenth century. It is assumed that optimum snow conditions for “maximum” avalanche reach have occurred at least once in every single avalanche track. From this point of view, avalanche reach might be calculated using terrain parameters only.
One basic idea in this work has been that the parameters chosen should be as objective as possible, and not be based on subjective judgement which may differ from person to person handling the problem. Ideally, one should therefore choose parameters which can be measured directly in the field or from maps.
As a first attempt the following parameters were chosen:
(1) Average gradient of avalanche path.
(2) Topography of starting zone.
(3) Inclination of starting zone.
(4) Supply of drifting snow to starting zone.
(5) Width of starting zone.
(6) Degree of confinement between starting zone and track.
(7) Average gradient of avalanche track.
(8) Total vertical displacement.
(9) Minimum curvature radius of path.
(10) Terrain profile of avalanche path.
1.3 Description of parameters
1.3.1 Average gradient of avalanche path α
This parameter is defined as α = arctan (H⁄L), where H is vertical height and L is total horizontal displacement. (Measured between the highest point of rupture and the outer end of the avalanche deposit.) The parameter has been used by Reference HeimHeim (1932), Reference ScheideggerScheidegger (1973, 1975), and Reference KörnerKörner (1976) to estimate average coefficient of friction, f= H⁄L. It is important to remember here that α is actually coupled to the motion of the centre of the mass of the avalanche (Fig. 1) (Reference KörnerKörner, 1976; also B. Schieldrop in the lectures referred to above).
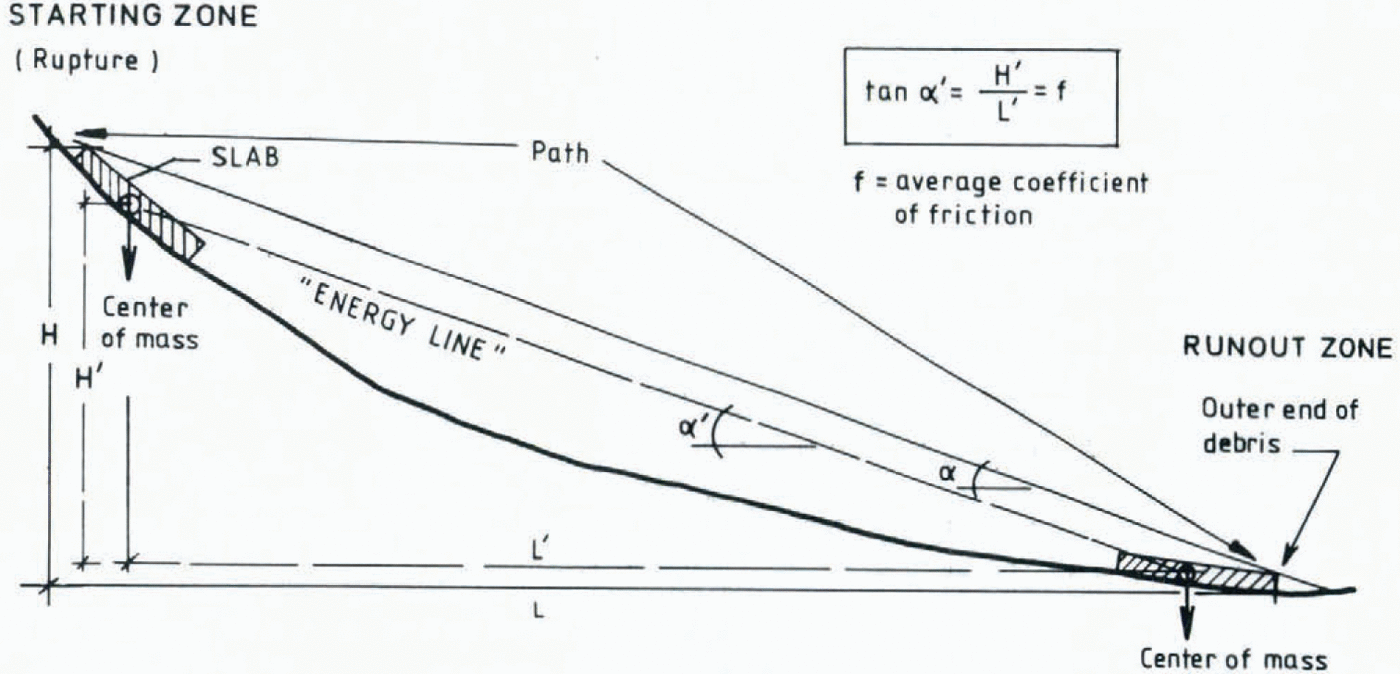
Fig. 1. Average gradient of avalanche path.
From a mechanical viewpoint centre–of–mass measurements would be the only logical way of describing α and f, but there are some practical difficulties related to a realistic definition of centre of mass in snow avalanches in Nature. Both Heim and Scheidegger have pointed out that α may be used as a criterion for avalanche reach, and since 1971, when the authors of this article started registration of avalanches, α has been chosen as a main criterion for avalanche reach. It is emphasized that these measurements are purely empirical, because the centre–of–mass position before rupture and after avalanche descent is impossible to measure.
On the other hand it is thought that distribution of avalanche debris related to centre of mass in different avalanches does not vary very much, and that centre of mass before rupture and after run–out are relatively the same in relation to the border of the mass. On open valley floors where run–out is not obstructed by distinct topographic formations, avalanche debris tends to spread out in a deposit where debris height is small in relation to horizontal distribution. Snow conditions when maximum run–out occur are also thought to be identical for the different avalanche paths, this also may give a fairly constant distribution of avalanche mass around the centre of mass in different avalanche paths. But it is underlined that there is a source of error here.
1.3.2. Topography in starting zone
It is known that avalanches frequently have their starting zones in different types of basins and depressions. It is also thought that total volume of avalanche snow in the rupture zone is dependent on the topography around the rupture, and that velocities and run–out distances may be functions of the avalanche volume. Rupture zones were therefore divided into five categories depending on their topography:
(1) Cirques (glacier–made basins).
(2) Shallow depressions (smaller depressions, river–made).
(3) Scars (deeply incised, narrow depressions).
(4) Flat faces (open, even surfaces).
(5) Convex slopes (slopes steepening down–hill).
Clearly there is room for subjective judgement whether the rupture zone should be classified in one or other group because of the gradual transition from one topographic formation to another is so common in Nature.
1.3.3. Inclination of starting zone
Frequency and magnitude of avalanches are partly dependent on rupture–zone inclination. On gentle slopes, about 25°–30°, the frequency is relatively low, because much snow must accumulate before rupture takes place. This again tends to create bigger avalanches than in steep rupture areas, where smaller snow amounts more frequently start sliding.
Inclination of rupture zone was measured on maps, scale 1 : 50000, and the distance between two adjacent hundred–metre contour lines at the upper border of the rupture point, were used as criterion for inclination.
1.3.4. Supply of drifting snow to rupture area
Flat–topped mountains and extensive plateaux windward of the rupture areas are known to be terrain formations where great amounts of snow can be eroded by wind and transported into the rupture zones. Whether such a topography creates avalanches with longer horizontal reach than avalanches having their origin in rupture areas surrounded by sharp mountain ridges, and where accumulation of snow occurs direct from the atmosphere, has been a matter of speculation.
Degree of drifting snow supply was divided into two groups:
(1) Starting zones surrounded by plateau–like hills and gently–inclined slopes with good possibilities for snow–drift supply, and
(2) Rupture zones surrounded by sharp ridges without erosion areas from whence snow can be collected.
1.3.5. Width of starting zone
Originally, starting–zone area was meant to be used as a parameter. But the down–slope borderline of the rupture zone proved to be difficult to define, especially for avalanches running on unconfined slopes, and consequently the estimation of rupture area was more or less a matter of guessing. Maximum width of rupture was therefore used as a description of rupture zone magnitude, as the maximum width may more easily be identified on maps and air photographs.
1.3.6. Degree of confinement between starting zone and track
A confined track is thought to create higher avalanche velocities than unconfined slopes (Reference Salm and CastelbergSalm, 1972; Reference Perla and MartinelliPerla and Martinelli, 1976). This effect of concentration was investigated by classifying avalanche slopes in three groups:
(1) Unconfined.
(2) Little to medium confinement.
(3) Strongly confined.
1.3.7. Average gradient of avalanche track
Avalanche track usually is defined as the portion of the whole avalanche length which lies between the rupture zone and the run–out zone. The lower boundary of the rupture zone proved to be difficult to define, because many slopes gradually decrease in slope angle, and often there are few topographic features that definitely draw the borderline between rupture zone and track. This is also the case for the transition between track and run–out zone; for most of the avalanches it was difficult to define the run–out starting point.
Average gradient of the avalanche track is defined as the inverse tangent of the ratio of the vertical fall between the upper boundary of rupture and the point in the path where the terrain gradient is 10° and the horizontal distance between the same points (β angle). The 10° point was chosen because it seems to correspond to the lowest value of the dynamic friction coefficient μ in avalanche snow (μ ≈ tan 10°) (Fig. 2).
The exact value of μ is not known and is unimportant here. The main reason for choosing 10° is that at slope angles around this value, it seems likely that retardation sets in. The 10° point was measured on maps to a scale of 1 : 5000 with a contour interval of 25 m.
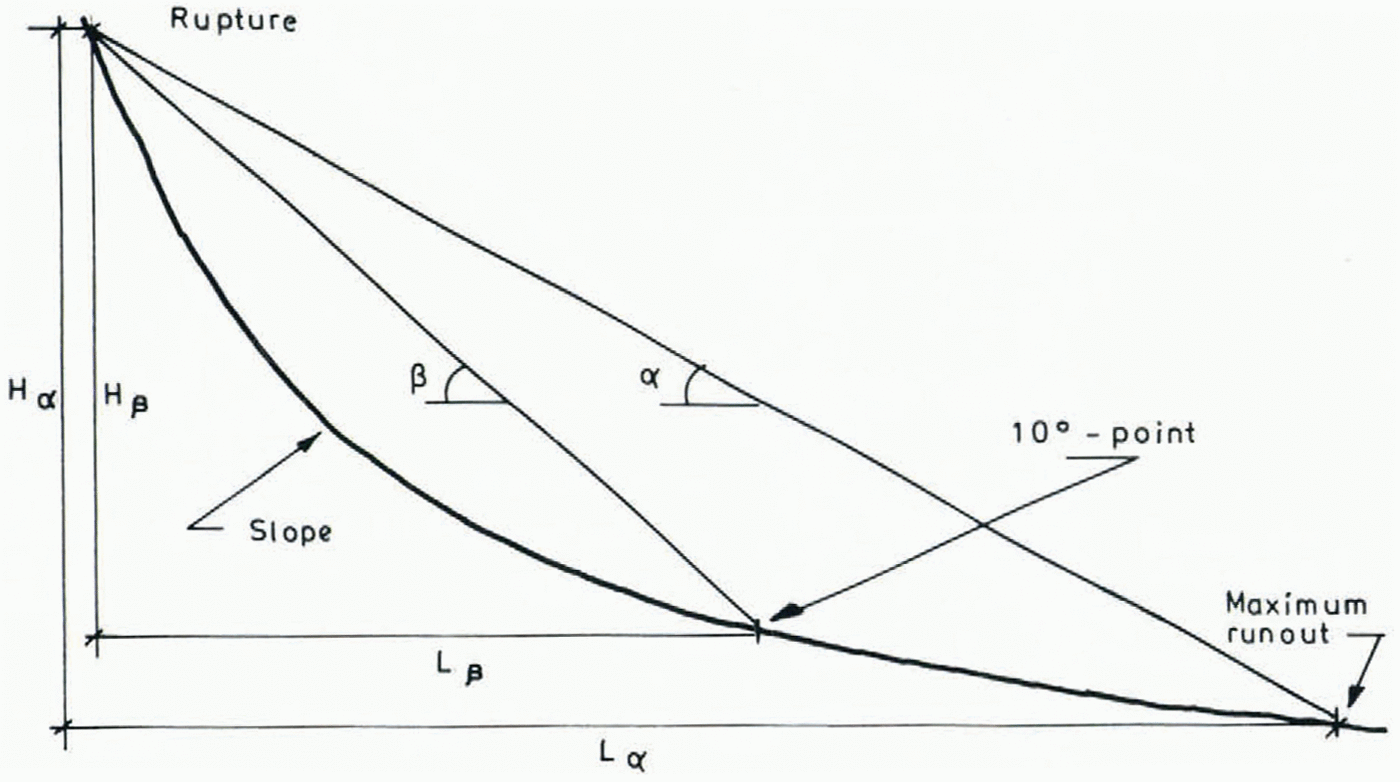
Fig. 2. Average gradient of avalanche track.
1.3.8 Total vertical displacement
Vertical displacements of avalanches were measured on maps between the uppermost boundary of rupture, and the lowest position of avalanche debris in the run–out zone.
1.3.9. Minimum radius of curvature of path
Radius of curvature in the transition zone between track and run–out area may cause a loss of energy and consequently is important for run–out distance as shown by Reference HeimgartnerHeimgartner (1977).
Minimum radius of curvature was found by a method in which the avalanche path was described as a fourth–degree polynomial. This polynomial could be handled mathematically and the radius of curvature found at each point. The III paths were plotted with vertical and horizontal coordinates, and the curvature equation was evaluated by the method of least squares. A regression analysis programme was used and a high correlation between real path and estimated path was obtained.
1.3.10. Terrain profile of avalanche path
As described in Section 1.3.9, terrain profile was calculated by regression analysis, originally by a fourth–degree function. The analysis showed, however, that a second degree function of the type y = ax 2+b, fitted the data just as well. Such a function has the property that its second derivative is a constant, and this constant determines the type of curve (gentle or steep) (from the lectures of B. Schieldrop already cited). This constant was therefore chosen as a parameter (Fig. 3).
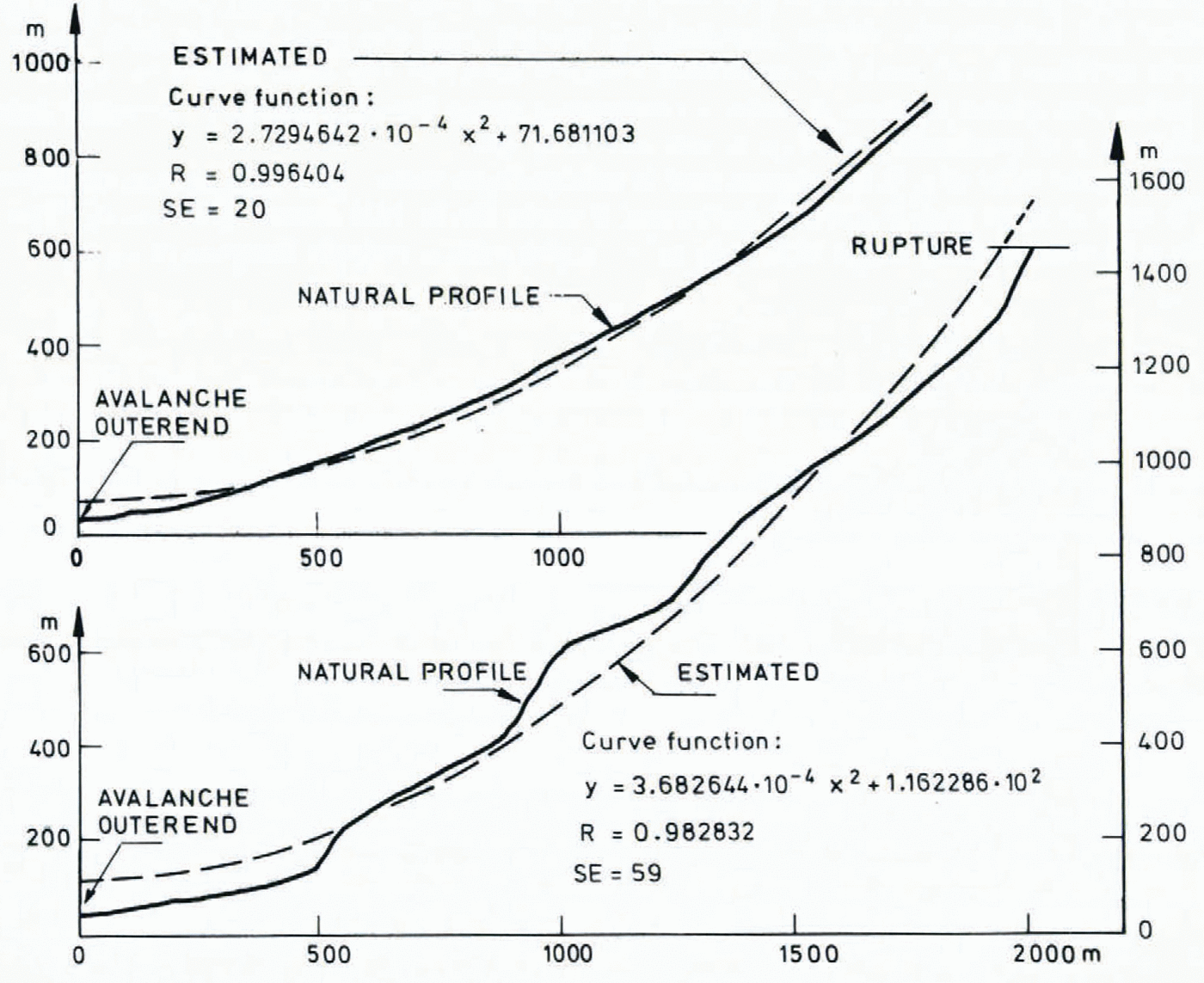
Fig. 3. Sketch of different types of avalanche slopes, real and estimated.
2. Results and discussion
2.1. Distribution of α angle
Median path gradients were measured for 423 avalanches. The scatter of α–values was, as expected, great, due to the variation of avalanche paths. The lowest value registered is 18°, the highest about 50°. The variation in α is seen from Table I.
TABLE.1 DISTRIBUTION OF α–VALUES RELATED TO FREUQENCY
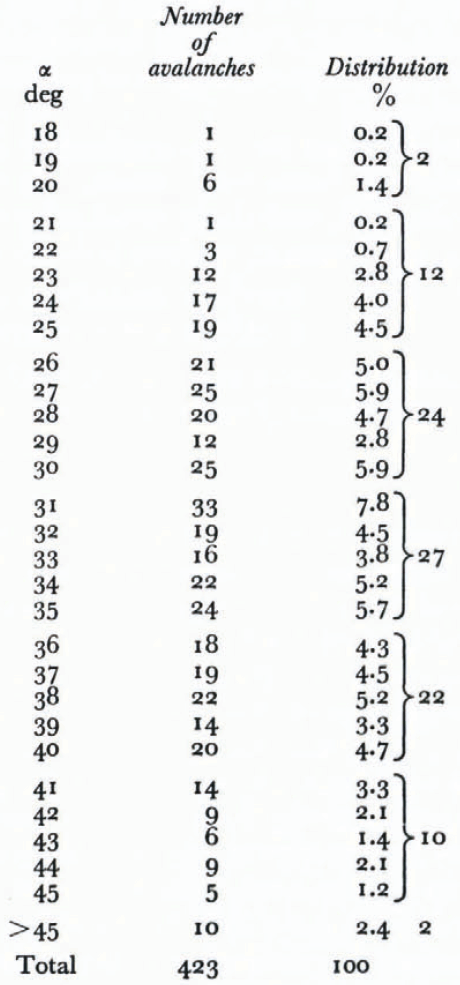
The variation indicates a normal distribution. The mean value is 33°, standard deviation, 6.3°. About 95% of the avalanches have a mean gradient greater than 23° and about 75% greater than 27°. Avalanches with a high α are most frequent, and are the avalanches easiest to identify. The paths with lowest α, <c. 25°, are of greatest consequences in land–use planning, because of their low frequency, and the long run–out distances of such avalanches.
If one assumes that dry friction μ is mainly responsible for movement resistance in avalanches running under optimum conditions for long horizontal reach, μ should be constant over the entire avalanche path. For avalanches running under such optimum run–out conditions, ploughing resistance and entrainment should be at a minimum.
The average gradient of avalanche path H⁄L might then be roughly equal to μ. The lowest observed α, 18°, corresponds to μ = tan 18° = 0.32.
2.2. Average gradient of avalanche track
A first attempt to explain the variation in α angles by terrain parameters was by use of the average gradient of avalanche track, the parameter β angle. This parameter was chosen to give a simplified expression of the track gradient, because it is evident that α angles are in a way connected to the general gradient of the avalanche slope. It seems likely that a gentle slope which is steep enough to keep the avalanche moving, will give a longer horizontal reach than a steep slope where more energy is lost in velocity–dependent resistance, like ploughing and entrainment (Perla, [c1980]). This last type of slope usually also has a marked transition between mountainside and valley floor, and the normal pressure, and hence the frictional force, increases according to υ2⁄R where υ is avalanche velocity and R radius of curvature of the slope. The relation between α and β was first investigated for avalanches reaching or passing the 10° point. Usually large avalanches reach or pass this point; 75 % of the registered avalanches did so in this investigation.
The ratio β⁄α has been worked out for 275 avalanches which all pass the 10° point. Maximum β⁄α = 1.32, minimum value, of course, = 1.0, mean 1.07. Standard deviation = 0.062. For all avalanches, both those terminating before the 10° point is reached and those reaching farther out, the following relation is found by regression analysis:

This close relation between α and β indicates that terrain profile of the entire avalanche slope is an important parameter for calculation of run–out distance.
2.3. Topography of starting zone
The starting zone topography was investigated to see if there is any relation to the value of α angle. Starting zones are grouped in five classes as described in Section 1.3.2.
The five groups are related to every 5° of α angle, and the results are presented in Table II. 9% of all avalanches have their starting zones in cirques, and 50% of the avalanches coming from cirques have their α angle equal to or lower than 25°. 19% have their origin in shallow depressions, and 19% of these again reach α ≤ 25°. 28% start in scars, but only 4% of the scar avalanches reach α ≤ 25°. 30% start from flat faces, and 8% of these reach α ≤ 25°. No avalanches from convex slopes reach α = 25°, although 14% start on such slopes. The results indicate that an avalanche starting from a cirque will have long horizontal reach, avalanches from shallow, open depressions too have good possibilities for long reach, and avalanches starting on flat faces and scars may also reach α <25°.
These parameters have not been quantified for handling by regression analysis. The subjectiveness in judgement and classification of the topographic features in the starting zone also makes these results questionable to some degree.
TABLE.II. Topography in starting zone. Percentage of each group related to α–angle

2.4. Degree of confinement between starting zone and track
Concentration or confinement of avalanche mass has been mentioned as a factor giving avalanches long run–out distances. Estimation of confinement is not particularly easy without subjective judgement. The three classes of confinement were defined in terms of the rupture width as follows: unconfined: rupture <2 times width of track; little to medium confinement: rupture 3–5 times width of track; strongly confined: rupture >5 times width of track.
Confinement does seem to imply longer horizontal reach, as 23% of class 3 reach α ≤ 25°, compared with 12% of all avalanches (Table III). 8% and 11% of class 2 and 1 respectively reach α ≤ 25°.
TABLE.III. Degree of confinement, in % related to α–angle

For class 3, 61% reach 25° < α < 35° while 49% of all avalanches reach these values. Class 3 then falls abruptly off as α increases to more than 35°. Class 1 and 2 seem to be more related to the total avalanche number for all α values.
For avalanches between 35°–40° the percentage decreases markedly from class 1 to 3. The results indicate that strongly confined avalanches usually have longer horizontal reach than unconfined and medium confined, and that strongly confined avalanches are scarce for α < 35°. The total number of class 3, 44 avalanches, are on the other hand too few to be quite representative.
2.5. Supply of drifting snow to starting zone
The effect of drifting snow is presented in Table IV. Fairly equal number of avalanches, 178 and 150 respectively, have their starting zones in the two groups. For α < 30°, the results indicate that terrain formations giving a high degree of snow–drift supply to rupture zone have no effect on avalanche run–out, as rupture zones with both high and little snow drift supply are equally represented in relation to all avalanches.
Obviously, this dividing into groups is also a matter of subjective judgement, and the classification may differ from person to person. The conclusion seems to be that snow drift supply from neighbouring terrain formations in general is not necessary in order to obtain avalanches with low α angles. On the other hand there may be certain terrain formations (Table IV)where snow–drift is important, for instance formations where a lee effect in itself is not obvious. Such formations are flat faces and shallow depressions. In topography like this, a supply of drifting snow from surrounding areas may accumulate more snow than the rupture areas are able to accumulate directly from the atmosphere alone.
TABLE.IV. Supply of drifting snow to starting zone, in related to α angle

where snow-drift is important, for instance formations where a lee effect in itself is not obvious. Such formations are flat faces and shallow depressions. In topography like this, a supply of drifting snow from surrounding areas may accumulate more snow than the rupture areas are able to accumulate directly from the atmosphere alone.
In Table V the supply of drifting snow is related to starting-zone formations. For cirques, scars, and convex slopes, the rate of snow-drift supply does not seem to be of importance. Avalanches from shallow depressions and flat faces have a markedly higher frequency of snow-drift supply. The explanation may be as indicated, that these formations have a lower degree of lee effect and therefore collect less snow directly from the atmosphere. For convex slopes the supply of drifting snow does not seem to mean anything, presumably because such formations are without any lee effect, and snow does not accumulate here because of wind transportation.
TABLE.V. Supply of Drifting Snow Related To Starting Zone Topography

2.6. Avalanches with specially low a values
Table VI contains avalanches with specially low α values. These results seem to indicate that starting–zone topographies formed as group 2; shallow depressions with a high degree of snow–drift supply, are most frequent at these low values of α angle. A high degree of confinement does not seem to be necessary, and starting–zone gradient also has great scatter. Great vertical fall height is not necessary to obtain low α angles, as avalanches with vertical fall of 370 m, a fairly low value, and of 1240 m, which is high, both reach α ≤ 20°.
TABLE.VI. Topographic formations for avalanches where α ≤ 20°
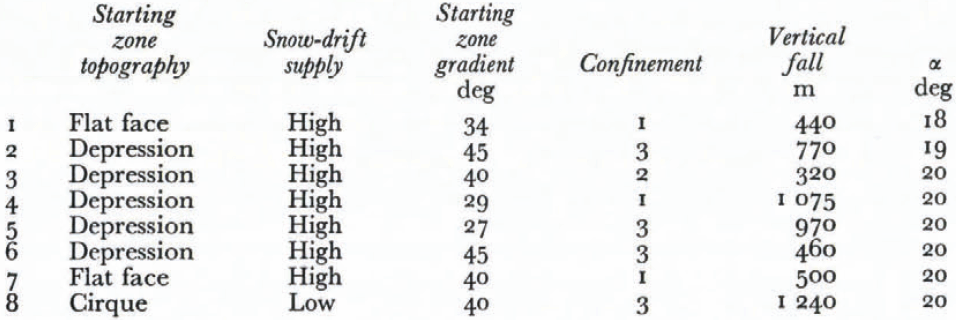
Only three groups of starting–zone topography are represented, “scars” and “convex slopes” have higher α angles. Lowest α angle for avalanche from “scar” is 24°, and from “convex slope” 27°.
Profiles of avalanches with α ≤ 20° are shown in Figure 4.
2.7. Regression analysis of topographic parameters
One way to solve the problem of estimating run–out distance in an empirical way, is by regression analysis of the different topographic parameters. The parameters examined in Section 2 are of different importance to run–out distance, and some are difficult to quantify and evaluate objectively. On this basis the following parameters were chosen:

The parameter minimum radius of curvature of path, proved to be difficult to handle. Minimum curvature was easily estimated by the program, but the extension of the zone in the path where the radius of curvature influences avalanche movement is not quite clear. This parameter is therefore not included in the analysis. The confinement of avalanche paths was divided into three groups in Section 2.4. In the regression analysis, confinement is described by the relation, Rmax⁄Tmin.
It is assumed that α angle can be written as a function of these parameters:
Regression analysis was then performed to find the five best equations with 1, 2, 3, and 4 variables respectively, describing the α angle. Calculations were done by an optimal, multiple-regression analysis program in FORTRAN (BakkehØi, unpublished) by a NORD–5 computer. The advantage of using an optimal multiple-regression program instead of a stepwise regression program, is that the best combinations of 1, 2, 3, and 4 variables will always be found. The independent variables are combined to make different functions, products, inversions, trigonometric functions, etc., of the parameters. It might therefore also be possible to find constants which could be combined with more dynamical models for run–out prediction.
2.8. Correlation of parameters
The parameter β gave, as described in Section 2.2, a high correlation with α (correlation coefficient R = 0.93, standard deviation of the residuals 2.44° for 275 avalanches). The regression analysis performed for eight parameters is based on III avalanches, including avalanches which, to a high degree, differ in height, avalanche mass, slope profile, etc. This (Fig. 4)is done to obtain a realistic composition of avalanche types. Correlation between α and β of these III avalanches gave R = 0.88, and the resulting equation, α = 0.97 β—1.4 °, with a standard deviation of 3.5°, gives high possibilities of variation in run–out distance.
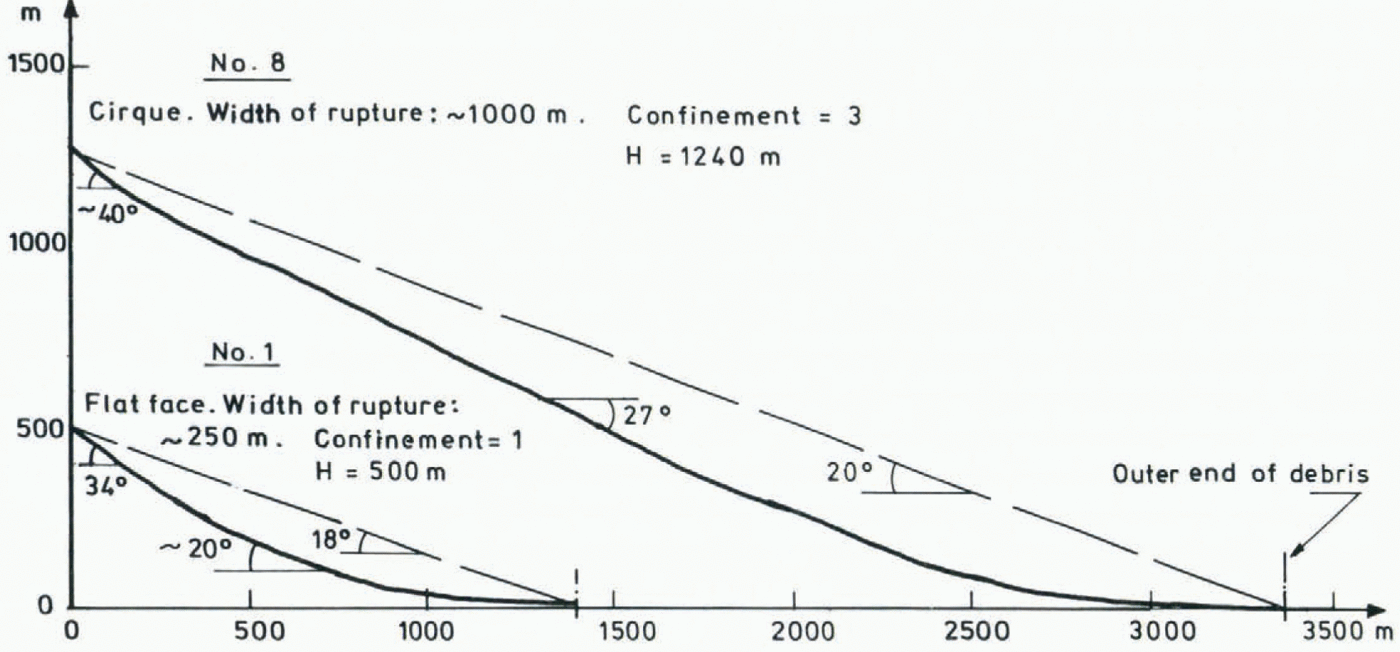
Fig. 4. Examples of profiles of avalanches with α ≤ 20°
The variable y’’ gave R = 0.80,
and the equation α=
(1.07✕104y’’+21)°. Standard
deviation, 4.4°. As a next step the product
Hy’’ was analysed. This gave the equation,
α= (1.17 ✕
10₊1Hy’’+ 21) °.
Standard deviation is 3.4° and R = 0.89. A much better
correlation is achieved when the analysis is performed with two variables. The
best equation for α is, ![]() .Standard deviation is
2.8° and R = 0.93. Another combination of the variables
gave α = 7.0✕10–1β+(4.8 ✕
103y’’ + 3.0)° and standard deviation was
2.9°, R = 0.92. The best equation without using the
parameter β is α = 1.7✕ 10–1θ+(1.1
✕ 10₊1Hy’’+1.5)°
with standard deviation 3.1°, and R = 0.91.
.Standard deviation is
2.8° and R = 0.93. Another combination of the variables
gave α = 7.0✕10–1β+(4.8 ✕
103y’’ + 3.0)° and standard deviation was
2.9°, R = 0.92. The best equation without using the
parameter β is α = 1.7✕ 10–1θ+(1.1
✕ 10₊1Hy’’+1.5)°
with standard deviation 3.1°, and R = 0.91.
In a combination of three variables the equation α = (6.7 ✕
10–1—3.2✕10–1Hy’’)
β +(2.1 ✕
10⁺1HY’’+9.3✕10–1)°
was obtained with standard deviation 2.5°, R = 0.94. A
more interesting equation is obtained by exchanging the expression
y’’Hβ with the angle
θ in the rupture zone. This gives an equation with a
correlation coefficient only 0.004 smaller than the first one. The equation is
![]() and the
standard deviation is again 2.5°.
and the
standard deviation is again 2.5°.
The best equation with four predictors was found when the variable θ was included in the equation giving the best result with three predictors,
Other combinations of the predictors give some higher standard deviations of the residuals with some lower correlations. The increase in the correlation coefficient when including four predictors instead of three is modest. With the parameters chosen it is not possible to obtain any significant increase in the correlation coefficient when equations with more than four predictors are used.
The analyses were performed with 26 independent variables ![]()
![]()
![]()
![]() .
.
The expression y’’H makes the profile independent of the total vertical displacement, and consequently all the profiles are scaled with dimensionless H. The philosophy behind this is that an avalanche path with small vertical displacement should have about the same value of α as one with great vertical displacement and the same shape, as mentioned in Section 2.6. From the analysis this seems to give a good result, and the equation α = (11.7Hy’’₊21)° has, as earlier mentioned, R = 0.89.
The parameters R max⁄T min and Dmax do not seem to improve the result, and neither do the expressions R max⁄T min, T min⁄R max,etc. The quotient R max⁄T min is an expression for the confinement of the avalanche path. This result is in agreement with Section 2.4.
The best equation with four predictors is found by using the angle θ, the angle β, the expression y’’H and y”Hβ. It is observed that a high θ gives a shorter run–out distance, which is natural. The avalanche will be triggered earlier because of the steeper slope and the mass involved will be smaller than in avalanches with a more gentle starting zone.
The parameter β itself gives a high degree of correlation, and this angle also describes the terrain profile to some degree. The predictor Hy” is a “dimensionless” double derivative of the terrain profile expressed as a parabola. The predictor y”Hβ is harder to explain physically.
An important question is how accurately it is possible to predict run–out distance. If one assumes the run–out zone to be horizontal, one can express the difference ΔL as

(L is the total horizontal displacement).
Assume H = 800 m, α = 25°, and Δα = —2.3° (one standard deviation). This gives ΔL ≈—195 m, which means that the avalanche reach is 195 m longer than the calculated mean value. Using the same numbers but Δα = 2.3°, one gets ΔL ≈ 164 m, which implies a 145 m shorter reach. For an avalanche with α = 25° and H = 800 m, the slope will be in the order of 2000 m, and standard deviation of 2.3° represents an error of 9 to 10% of the total slope of the avalanche.
To illustrate the method, an avalanche path in Valldal in western Norway, is chosen as an example. Observations of this path go back two hundred years, and the avalanche is observed to have a maximum run–out which gives α = 25.5°. The best parabola fitting the slope is expressed as, y = 1.54 ✕ 10–4x 2—4.8. This gives y” = 3.08-10–4. The inclination in the rupture zone θ = 36.5°, β = 34°, and H = 1 260 m. The calculated equation is,

The difference is 1.3° and is less than the standard deviation of 2.3°.
The most important parameter is the β. Hy” is also an important parameter while Hy’β and θ are less important. In this example the run–out zone was almost horizontal, and the vertical height H is easy to find. In cases with steeper run–out zones one must first assume the most probable place for the avalanche to stop, then find the height and calculate the α. With this α one is able to find another H and then calculate a better α. This iterative process can be repeated until no significant change in H occurs.
3. Acknowledgements
The authors wish to express their appreciation to the persons who made this work possible: The farmers living in the avalanche districts who supplied us with information on avalanche behaviour, K. Kristensen who did much of the field work, B. Reite and U. Domaas who accomplished a great deal of data treatment. Valuable discussions have also taken part between the members of the avalanche group at NGI, and we are also grateful to B. Schieldrop, for his suggestions and ideas throughout this work.


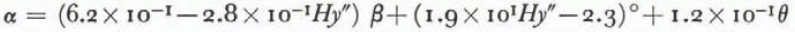 has a correlation coefficient
of 0.95 and standard deviation of 2.3°. This relationship makes possible
a fairly accurate prediction of avalanche run–out distance.
has a correlation coefficient
of 0.95 and standard deviation of 2.3°. This relationship makes possible
a fairly accurate prediction of avalanche run–out distance.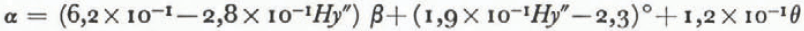 a un coefficient de
corrélation de 0,95 et un écart-type de 2,3°. Cette
relation permet une prévision précise de la distance
d’arrêt possible de l’avalanche.
a un coefficient de
corrélation de 0,95 et un écart-type de 2,3°. Cette
relation permet une prévision précise de la distance
d’arrêt possible de l’avalanche.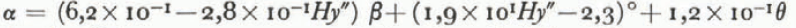 hat einen
Korrelationskoeffizienten von 0,95 und eine Standardabweichung von 2,3°.
Diese Beziehung ermöglicht eine recht genaue Voraussage der
Lawinenreichweite.
hat einen
Korrelationskoeffizienten von 0,95 und eine Standardabweichung von 2,3°.
Diese Beziehung ermöglicht eine recht genaue Voraussage der
Lawinenreichweite.









