A rheological model, based on till dilatancy (shear thickening)

At a time when most ideas of drumlin formation were focused on either sediment deposition or erosion, the first conceptual leap of the new rheological model was that both might occur together if, beneath the glacier, there was a layer of lubricating sediment that ‘flowed’ and therefore was able to conduct geomorphic work (erosion, deposition, shaping) of its own. In this model, attention focused on what the lubricating sediment could produce rather than expecting the overlying ice to cut or deposit drumlins. This was a good idea and, in the quest for understanding how drumlins are created, Reference Smalley and UnwinSmalley and Unwin (1968) appear to have invented the concept of glacier flow by subglacial sediment deformation, prior to any observations of it occurring (which came much later: Reference BoultonBoulton and Jones, 1979; Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1986). They proposed the basic conditions necessary for the formation of drumlins in the following words:

• i) The glacier-terrain relationship [which we now call ice- bed coupling]… was such that at the base of the glacier the terrain material was being continuously deformed. Some of this terrain material [now called the deforming bed] … was carried along by the glacier so that shear deformation occurred within the terrain material.

• ii) The deformed layer was composed of a concentrated dispersion of boulders and large rock particles in a dense clay-water system … For drumlins to form, the large particles in this till layer had to form a dilatant system. (Reference Smalley and UnwinSmalley and Unwin, 1968, p.378)

Their second advance was the argument that parts of the till layer have the rheological property of dilatancy and that this is a means of thickening the deforming till layer, offering an explanation of how relief is created to make a drumlin. Unfortunately, there are somewhat overlapping definitions of dilatancy which appear to be used in glaciology without distinction. One regards a dilatant till as simply one that has expanded (dilated) by enlarging pore spaces with water. Modern glaciology appears to use this definition when referring, for example, to dilatant tills beneath Antarctic ice streams, where seismic profiling is used to detect dilatant till which is presumed to be likely to be deforming. A soil mechanics definition considers a material dilatant if it expands when subjected to a stress because of a rearrangement of the particle-to-particle packing of the components. In physics, the term is used to describe non-Newtonian fluids in which viscosity increases with shear rate and which are either called dilatant or rheopectic (dependent upon the response over time). This use of dilatancy is in the opposite sense to that above, in that a dilatant till has become stifferand more resistant to deformation. Smalley and Unwin appear to have used the term to imply both an expansion and a stiffening of the till body. In material engineering, this behaviour is also called shear thickening and is widely used, for example, in viscous couplings on four-wheel drive cars. Here a shearthickening fluid is used as a kind of clutch to engage four- wheel drive when the wheels on one axle are slipping, generating shear in the fluid, which then thickens it enough to transmit drive to that axle. In drumlinology the weight and movement of the glacier, according to Reference Smalley and UnwinSmalley and Unwin (1968), transmits shear stresses into the till, straining it enough to promote shear thickening (dilatancy) in some places which expand (relief amplification) to become the cores of drumlins, and which act as stiff obstructions in the flowing till. Also recruited is the opposite material behaviour, shear thinning (also called thixotropy), which responds to increased shear stresses by becoming less viscous and flowing more easily. Ketchup is a shear-thinning material, which is why shaking or pressurizing it makes it come out of the bottle more easily and often splat further than intended. If parts of the till have become shear-thickened and expanded (making bumps in the till layer) and parts have become shear- thinned, then the latter material can flow more easily and is presumed to move between the bumps (proto-drumlins), gradually reshapingthem into streamlined forms, as occurs in most fluid-obstruction interactions, producing streamlined bumps called drumlins. Figure 3 illustrates this process.

Fig. 3. Although intended for a slightly different explanation (see later), this figure reproduced from Reference Boyce and EylesBoyce and Eyles (1991) illustrates how shear-thickened and shear-thinned tills could produce drumlins in the spirit of Reference Smalley and UnwinSmalley and Unwin (1968). Consider a pre-existing flat plain of till with spatially variable concentrations of rock fragments, clay and water. Glacier-induced stresses stimulate some of the more rock-rich parts of the till body into shearthickening behaviour (dilatancy) producing stiff patches of till that expand into bumps (T1). Other parts of the till are shear-thinned and can thus flow more easily as streams of clay-rich sediment (arrows). Over time (T1–T3) such ‘streaming till’ shapes the bumps into drumlins. Essentially this is the rheological model of Reference Smalley and UnwinSmalley and Unwin (1968). Figure reproduced from the journal Geology with permission of the Geological Society of America (# GSA 1991).

Presumably realizing that the notion of tills continually deforming beneath an ice sheet was a radical one (see also later work: Reference Hart and BoultonHart and Boulton, 1991;Reference Hicock and DreimanisHicock and Dreimanis, 1992;Reference Piotrowski, Mickelson, Tulaczyk, Krzyszkowski and JungePiotrowski and others, 2001), Reference Smalley and UnwinSmalley and Unwin (1968) also proposed a side argument for drumlin generation that did not require it. In this model they presumed the glacier was overriding a till sheet with pre-existing stiff patches and that these became drumlins. ‘While the till with loose packing of boulders was easily smeared across the landscape, the till patches with the higher boulder content were obstinately dilatant’ (Reference Smalley and UnwinSmalley and Unwin, 1968, p. 380). This idea was further developed by Reference Boulton, Menzies and RoseBoulton (1987) and is illustrated in Figure 4.

Fig. 4. This picture, reproduced from Reference Boulton, Menzies and RoseBoulton (1987), illustrates Smalley and Unwin’s alternate means of drumlin production, whereby preexisting stiff patches are overridden by the glacier and progressively shaped by erosive streaming debris, into drumlins. In Boulton’s evolution of the idea, the stiff patches are not controlled by shear thickening (dilatant boulder concentrations), but by differences in permeability acting on material strength via its ability to influence pore-water pressures. Copyright © 1987. From Boulton, G.S. A theory of drumlin formation by subglacial sediment deformation. In Menzies, J. and J. Rose, eds. Drumlin Symposium. Reproduced by permission of Taylor and Francis Group, LLC, a division of Informa plc.

The accomplishment of the rheological model for drumlin formation is that it can make bumps that then become streamlined (true drumlins if you like) or it can merely streamline pre-existing bumps or stiff patches to make them look like drumlins (perhaps cheat drumlins or drumlin clones). While a clever idea, and pre-dating the wider appreciation of deforming beds, unfortunately the subsequent literature appears not to have quantified the extent to which drumlins have different sediment rheologies than inter-drumlin sediments.

Drumlin formation by subglacial sediment deformation

The idea of a layer of sediment steadily deforming beneath ice sheets continued to feature in discussions of drumlin formation in the Journal. In a published abstract, Reference BaranowskiBaranowksi (1977) questioned whether dilatancy could occur at the glacier base with enough change in the mechanical properties to be able to create drumlins. Unfortunately the paper was never presented, as Stanisfaw Baranowksi perished after an accident in Antarctica. Touchingly, his ideas were followed up in a paper by Ian Reference SmalleySmalley (1981) which was dedicated to Baranowksi. Rather than dilatancy to form stiffer cores to make drumlins, Baranowksi proposed that drumlins might form in a deforming bed when the thermal regime changed from warm- to cold-based. At some point in this transition, frozen patches in the till could become the stiffer cores (Reference BaranowskiBaranowski, 1977). Reference SmalleySmalley (1981) also reviewed the ideas of Reference BoultonBoulton (1979), noting the similarity to his own rheological model but that it appealed more generally to inhomogeneities in till rheology rather than dilatancy itself.

Soon after the early observations of deforming beds, Reference Boulton, Menzies and RoseBoulton (1987) was quick to galvanize ideas such as noted above into his seminal paper presented at the first International Drumlin Symposium. His ‘theory of drumlin formation by subglacial sediment deformation’ is remarkable in that it appears to provide, for the first time, a universal explanation for drumlins and related bedforms. Up until this point, theories tended towards explanations of particular drumlin types. The theory is so complete in detail that it purported to be able to explain most observed internal structures and landscape settings. The main ingredient has already been explained (e.g. Fig. 3), that of a mobile and deforming bed that thickens in places to produce bumps that then become streamlined into drumlins. There appear to be two basic mechanisms for thickening the till layer into such bumps, and one for shaping pre-existing bumps or stiff patches of till into a drumlin shape, which Reference HartHart (1997) categorized into depositional, deformational and erosional drumlins. I informally name these components and their resulting drumlin types:

• Erosional shaping by streaming till. This is illustrated and explained in Figure 4, and is where a stronger patch of till (e.g. coarser-grained and better-drained) acts as a resistant body in the otherwise flowing till and is progressively shaped to produce what I term drumlin clones. When examined in section, they are likely to have cores of more resistant material such as gravel, and often a thin sheath of highly deformed till. Reference Boyce and EylesBoyce and Eyles (1991) provide excellent evidence for such a mechanism in the form of pre-existing horizontally bedded glacial deposits that are interpreted to have been carved into bumps by deforming till streams.

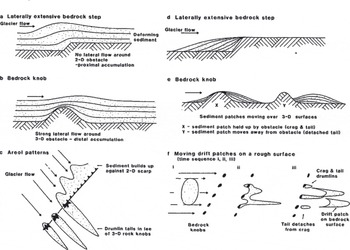
• Agglomeration at obstacles. As with the transport of, say, sand, by wind or water, obstacles in the path of the flow may become foci for deposition. Reference Boulton, Menzies and RoseBoulton (1987) sketched the main types of obstacle (i.e. bedrock knob or step) that flowing till may encounter (Fig. 5) and deduced the kind of till agglomeration that might occur. Crag-and-tails clearly fall into this category, but there are many variations on this theme including pre-crags (i.e. ‘tail in front’; Reference Haavisto-Hyvarinen, Kielosto and NiemelaHaavisto-Hyvarinen and others, 1989). In a large area of Sweden, for example, Reference MöllerMöller (1987) claims that most drumlins have bedrock knobs associated with them. I group all these types together and call them obstacle drumlins.

  

  Fig. 5. Mobile till may encounter bedrock knobs and steps, and much like any other mobile medium (wind or water, say) that encounters obstacles, these may become foci for attachment or deposition. Here we name these as obstacle drumlins. Note that while some obstacle drumlins are likely to exist in the bedforms shown in Figure 2, it is improbable that they can all be explained in such a manner. Copyright © 1987. From Boulton, G.S. A theory of drumlin formation by subglacial sediment deformation. In Menzies, J. and J. Rose, eds. Drumlin Symposium. Reproduced by permission of Taylor and Francis Group, LLC, a division of Informa plc.

• The rheological sandwich. Here the drumlin is proposed to form by (tectonic) folding of surfaces within the till. These folds produce the bump, or drumlin core, around which streamlining can then occur. The idea is based on a sort of rheological sandwich, with deforming ice as the upper layer and two layers of till, an upper rapidly deforming and dilatant (in the sense of expanded) ‘A’ horizon on top of a more stable consolidated ‘B’ horizon. Folding is presumed to be initiated across this boundary. Folding is thought to occur due to downstream differences in the viscosity of the till, with folding initiating upstream of stiffer portions. An appeal of this hypothesis is that we can imagine drumlins spontaneously appearing in numerous locations (viscosity changes are likely to be common) without the requirement of convenient bedrock knobs, for example.

Drumlin emergence and self-organization

Again, what is the most important observation about drumlins from which to build a theory: the sediment, the shape or their distribution? The theories thus far have sought explanations of sediments and shape, but not the distribution (pattern). When examining subglacial bedforms at remote-sensing scales, the overriding observation is the ubiquity of the forms across vast areas (Fig. 2) and some kind of regularity to their positioning within the field. Given that bedform shapes vary widely (Figs 1 and 2) and that those investigating internal structures of drumlins have yet to find a defining or characteristic sedimentology (rather, they vary enormously) then here I argue that the primary property of drumlins and related bedforms is their regularity of arrangement in fields; they seem to constitute a pattern phenomenon (Fig. 2 is striking in this regard). If this is true, then the explanations of Reference Boulton, Menzies and RoseBoulton (1987) seem inadequate to explain such patterns: would such anchoring at bedrock knobs or the existence of pre-existing bumps or inhomogeneities really be positioned so widely and regularly? It seems unlikely, and so leads to the notion that there must be a means of generating what I call emergent drumlins. Emergent drumlins are those that spontaneously arise in the bed, as a consequence of presumably ice, bed and water interactions, and do not require a pre-existing spatial template of imperfections. This seems an appropriate name to reflect, at the simpler level, that they do not have a specific easily identified ‘reason’, they just spontaneously emerge from the bed. Or they can be thought of as true emergent phenomena: ‘the arising of novel and coherent structures, patterns and properties during the process of self-organisation in complex systems’ (Reference GoldsteinGoldstein, 1999, p.49).

Reference Smalley and UnwinSmalley and Unwin (1968) have been along this line of thinking before (drumlin distribution), but because their rheological-dilatancy theory required sediment inhomogeneities in the till, their hypothesis was that drumlins should therefore reflect such distributions which they presumed to be random. As a test for this, they conducted two sets of analyses, the first of which used random-number tables to model the position of idealized drumlins within a field, whose drumlin-to-drumlin spacings were measured and compared with those of a real drumlin field. Similarity was found in the frequency distributions of spacings for the modelled and real fields. The second method calculated the Euclidean distance between adjacent drumlins within four drumlin fields and performed nearest-neighbour analysis, yielding a statistic that can be used to determine if the distribution of elements tends towards clustering, random or regular (uniform). From both sets of analyses Reference Smalley and UnwinSmalley and Unwin (1968) concluded that the examined fields contained a random distribution of drumlins, thus supporting their theory. Unfortunately, the nearest-neighbour analysis suffered some problems in execution. Such analysis is designed for point patterns and yet drumlins possess an area, which of course prevents points from getting close together and therefore biases the analysis by steering the statistic away from clustering. In another Journal paper (Reference Boots and BurnsBoots and Burns, 1984) this problem was noted and a ‘two-phase mosaic’ approach developed and applied to drumlins as areas (rather than points), and also yielding a pattern not significantly different from random. However, the other and larger problem in nearest-neighbour analysis is the extreme sensitivity of the statistic to the size of area used, and, as Unwin later acknowledged (Reference UnwinUnwin, 1996, p. 545), ‘by total (mis)chance I seemed to hit on the scale of analysis that produced values close to the magical random expectation’. Reference BaranowskiBaranowski (1977) seems to share my earlier expressed view (of regularity rather than randomness in pattern). He analysed lateral spacings of drumlins and devised a statistical scheme for assessing their degree of regularity to randomness, finding his sample to be ‘partly regular, and partly random’. The analysis was thus not conclusive, but he argued that there was sufficient evidence for the existence of a mechanism regularizing the development process of a drumlin field. It is clear that assessment of regularity of drumlins has thus far yielded imperfect results and with some contradiction, and also has only been conducted with fairly small (hundreds) samples. In the absence of firm evidence, I appeal to the appearance of a pattern in Figures 1 and 2, and of course recognition of a pattern necessarily implies regularity. Also, for the related phenomenon of subglacial ribs (ribbed moraine), spectral analysis of their downstream spacing (on transects totalling 12 000 km) reveals clear concentration of power at preferred wavelengths, thus demonstrating a distinctly non-random distribution in space (Reference Dunlop and ClarkDunlop and Clark, 2006). I suppose that, when appropriately analysed, drumlin fields will have the same property.

Contrary to the earlier indications of randomness, in their later papers Smalley and colleagues also express the view that drumlin fields actually comprise a pattern, by comparing them to the dimples of a golf ball (Reference Smalley and WarburtonSmalley and Warburton, 1994;Reference Smalley, Lu and JeffersonSmalley and others, 2000). Intriguingly, they take this comparison further and ask why (rather than how) drumlins form, and using the golf ball analogy (the dimples reduce aerodynamic drag) suggest that ‘the ground/ interface/glacier system organises a flow-promoting ground geometry, which we call a drumlin field’ (Reference Smalley, Lu and JeffersonSmalley and others, 2000, p.32). They thus wonder whether the growth of drumlins reduces drag and promotes faster ice flow. A dimpled golf ball flies further than a smooth equivalent because the sum of the drag from the dimples (numerous small drag vortices) is less than from a larger boundary-layer separation at the scale of the ball itself (Reference Smalley, Lu and JeffersonSmalley and others, 2000). Transferring this situation to ice is not appropriate because ice flow is not turbulent as indicated by its Reynolds number, but the question remains interesting: why does an ice sheet seek to make its smooth beds rough? Reference SchoofSchoof (2002) attempted to work out how much resistance drumlin-scale bumps could provide to ice flow and whether they could act as regulators of flow speed, but it appears that the question remains unresolved.

Instability in the coupled flow of ice and till

Early views regarding drumlins tended to emphasize their rareness and that some special conditions must have been satisfied to permit their formation. Scrutiny of former ice-sheet beds using satellite images and digital elevation models (DEMs) (Reference ClarkClark, 1997) has taken us away from the view of drumlins as special cases to seeing them as extremely widespread and as ubiquitous phenomena (e.g. Reference Prest, Grant and RamptonPrest and others, 1968;Reference Greenwood and ClarkGreenwood and Clark, 2008; Reference Hughes, Clark and JordanHughes and others, 2010). It has been estimated (Reference Clark, Hughes, Greenwood, Spagnolo and NgClark and others, 2009) that drumlinized terrains cover some 70%, 50%, 40% and 15% of the glaciated area of Canada, Ireland, Scandinavia and Britain respectively. It seems that whenever ice flows over soft sediments, bedform production is inevitable. Along with the supposed patterning discussed above, this strongly argues for a unifying theory of formation and points to a serious limitation in all theories discussed thus far. It surely cannot be sensible to rely on special sediment inhomogeneities or pre-existing bumps (i.e. templates) to explain all or most drumlins;there just has to be a mechanism for generating emergent drumlins as a matter of course. Such a mechanism is the ‘missing link’: what generates the pattern?

By the 1990s the deforming-bed circus was in full swing, with numerous papers exploring implications regarding ice- sheet stability, ice streaming, sediment transfer, etc. Treating ice-sheet beds as a mobile ‘flowing’ medium prompted a new way of thinking about till, and fluid-dynamical principles were brought to the fore. Reference HindmarshHindmarsh (1996) developed a numerical model of till patches sliding and deforming across bedrock and producing kinematic waves. It was realized that the migration speed was dependent upon the effective pressure at the base of the till and that this varied due to the till thickness. An implication of this is that upstream-moving kinematic waves (till-thickness variations) might occur, as well as abrupt jumps in till thickness (shock waves, which were often found to be asymmetric). Here was a fluid-dynamic reason for relief amplification, and given that drumlins were classically described as having steep stoss ends (although see Spagnolo and others, in press) the possibility was raised that drumlins might be asymmetric shocks in a flowing medium. Essentially the theory says that an infinitesimally small bump increases the effective pressure just upstream of the bump, thereby reducing the mobility of the ‘flowing’ sediment at depth in the till. To overcome this, a higher till flux is produced near the ice-till interface. When more till flows into the bump than out, the bump grows. The model, however, was only really applicable to thin till patches sliding across bedrock, yet most drumlins appear to be undulations in the upper surface of thick (>10m) till sheets.

From such thinking it seems that the missing link in drumlinology was found when Reference HindmarshHindmarsh (1998a, Reference Hindmarshb) wondered whether the coupled flow of ice and subglacial sediment might be inherently unstable, such that the ice-till surface could become spontaneously wavy (an abhorrence of flatness). If water or air flowing over a sandy surface can generate regular bumps that we recognize as patterns (and call ripples or dunes), then since drumlins and subglacial ribs are just bumps in a till surface, could a similar mechanism create them? There is nothing specific in the transport of a sand grain, by water or wind, which tells it to pile up in ridges of regular spacing, but the system is clearly self-organizing and the dunes are emergent phenomena. Such causation is difficult to understand intuitively, but it is now well known that the regularity of spacing is a consequence of an instability (i.e. a mechanism that chooses to amplify tiny disturbances) inherent in sand transport (Fig. 6), and that from a flat plain, ridges will grow at a certain wavelength (spacing) (e.g. Reference PrigozhinPrigozhin, 1999). In fact, ridges are trying to grow at most wavelengths but the instability determines that one wavelength will be the most rapidly growing and it is this one that usually emerges. Numerous examples exist more widely in nature, producing patterns from inherent instabilities in systems such as the Rayleigh-Taylor instability which occurs when a dense fluid is being accelerated by a light fluid (Reference SharpSharp, 1984), or the Kelvin-Helmholtz instability which drives some cloud formations (Reference DrazinDrazin, 2002) and produces (ocean) waves at the water-air surface, driven by winds.

Fig. 6. Instabilities in sand transport by water, across this beach, have yielded a self-organization comprising ridges, orthogonal to flow at ~10cm spacing, and on this occasion with (drumlin-like) streamlined culminations upon the ridges. The resemblance of such landforms (form analogies) to subglacial bedforms inspired Reference ShawShaw’s (2002) subglacial flood theories where the actual medium (water) is proposed, and motivated the Hindmarsh–Fowler instability theory where the mechanism (instability) is proposed.

Two Journal papers (Reference HindmarshHindmarsh 1998a, Reference Hindmarshb), sought out such instabilities in the coupled flow of ice and sediment. The first of these performed perturbation analysis using ice as a linearly viscous fluid, and the underlying till as having a power-law dependence on stress and effective pressure. The analysis restricted itself to a linearized set of equations and was able to show that instability occurs and infinitesimally small perturbations should grow (under certain parameter regimes), but the method could not predict the amplitude of such bumps. In the second paper, which more directly addresses drumlin formation, bump generation in thicker tills was analysed, and the nature of shock behaviour was explored, yielding up- and downstream travelling waves. Such waves might run into each other to coalesce, producing up- or downstream facing blunt (steeper) faces. The vexed problem of what form of rheology till actually possesses (e.g. the viscous vs plastic debate) was aired and it was supposed that this might depend on the scale being examined. If the perturbation analysis (Reference HindmarshHindmarsh, 1998a) is thought of as the seeding of drumlins, the other aspect, shaping, is also important in any drumlin theory and the Reference HindmarshHindmarsh (1998b) paper modelled the evolution from circular or square initial bumps into more streamlined drumlin-like forms.

Having developed the theory of instabilities seeding drumlins and generating relief, Reference HindmarshHindmarsh (1999) explored what this meant for the distribution (spacing) of drumlins in a field and thus started to address the patterning. The main new ingredient over the earlier papers was that rather than presuming near-perfect coupling between ice and the deforming sediment he allowed for sliding to occur at the ice-till as well as the till-bedrock surfaces in addition to deformation within the sediment body (Fig. 7). Such a system of deformation and slip of layers of varying physical properties is an environment prone to the development of instabilities (Reference SharpSharp, 1984). This two-dimensional (2-D) instability modelling (single downstream flowline) predicted the growth rate of bumps and the (dominating) wavelength at which they should grow (Fig. 8). This of course varies according to the parameter settings (ice velocity, effective pressure, etc.). The growth rate informs us of how fast such bumps should grow, and thus how long it takes to produce a bump (only decades), and the wavelength tells us that the bumps should have a downstream spacing of hundreds of metres.

Fig. 7. In Reference HindmarshHindmarsh’s (1999) model, both ice and sediment are allowed to deform, and sliding can occur at both the ice–till and till–bedrock surfaces. Such a system of deformation and slip of layers of varying physical properties is an environment prone to the development of instabilities. Model runs start with a flat till surface (a), and under certain parameter settings (e.g. ice velocity, effective pressure) the ice–till surface becomes wavy (b).

Fig. 8. A typical output from the 2-D Hindmarsh model (1999). For a till depth of 10 m, ice velocity of 100m a^–1 and with effective pressure and shear stress of 0.5 bar, instability in the system is predicted to occur. For this parameter set, the solid curve indicates that the maximum growth rate occurs with a 300m wavelength, so bumps of this downstream spacing are predicted to grow.

Pursuing the same line of reasoning and basic physics, Reference Fowler, Maltman, Hubbard and HambreyFowler (2000) developed a mathematical model explaining how dunes and antidunes arise from natural instabilities in the transport of sediment along river beds and then used this to derive an analogous model for the flow of ice over a sedimentary bed. He demonstrated analytically that ice flow over a deformable till nearly always produces instability. This added credence to the analysis performed by Reference HindmarshHindmarsh (1999), and among other things reassured us that the instability is likely to be real and not, for example, a numerical artefact, and confirmed that the downstream spacing should be of the order of hundreds of metres. Fowler showed that the bumps migrated downstream at a rate slightly less than the basal ice speed.

In their excitement these early papers prematurely (and now confusingly) claimed that the instability would generate drumlins, but in fact the instabilities were only demonstrated to occur in the downstream direction, which best explains ribbed moraine. Drumlins are true threedimensional (3-D) landforms and clearly have lateral spacings, as yet unexplained. Retreating from drumlins for a while, Hindmarsh renamed his theory the Bed Ribbing Instability Explanation (BRIE) and formulated it as a numerical model which was run many millions of times with different parameter sets to make predictions of the wavelength (spacing) of ribbed moraine. Reference Dunlop, Clark and HindmarshDunlop and others (2008) compared these predictions with an extensive dataset of spacing measurements from Canada, Ireland and Scandinavia, and the instability model was found to correctly predict wavelengths that exist in nature (Fig. 9).

Fig. 9. The model (BRIE) was run with 529 200 different parameter permutations thought to be appropriate for ice-sheet flow. (a) The predicted range and distribution of wavelengths and (b) spacing measurements of real ribbed moraine in Canada, Ireland and Scandinavia along downstream transects totalling 12 000km (from Reference Dunlop and ClarkDunlop and Clark, 2006). Graph reproduced from Reference Dunlop, Clark and HindmarshDunlop and others (2008), where they note that the model predicts wavelengths of the appropriate order and with a similar modal preference for ~350 m. Extremely large subglacial bedforms (Reference Greenwood and KlemanGreenwood and Kleman, 2010) resembling waves in till thickness (ribbed moraine) have recently been reported in Canada, with wavelengths of ~6 km. These clearly extend the range in observations (b) upwards, but they still fall within the wavelength predicted by the model runs.

Reference SchoofSchoof (2002, Reference Schoof2007) re-examined the Hindmarsh-Fowler instability mechanism, confirming that such an instability arises, but only in the downstream direction, suggesting that the mechanism was unable to predict drumlins. Given the ensuing debate on the (plastic vs viscous) rheology of till (e.g. Reference HindmarshHindmarsh, 1997;Reference Iverson, Baker and HooyerIverson and others, 1997;Reference MurrayMurray, 1997;Reference FowlerFowler, 2003), Schoof performed an analysis across these behaviours, noting that it did not much matter to the presence of the instability. However, he also found what he regarded as a killer problem. Shortly after bump generation, his model predicted that cavities would form just downstream of the shock (bump) and these could limit bump growth such that the instability mechanism would be unable to produce landforms of the appropriate relief (~10m). Analysis of bump growth by instabilities and simultaneous treatment of lee-side cavitation is apparently a taxing mathematical problem, and one that stalled theoretical developments for a while. Reference FowlerFowler (2009) added a mathematical technique to deal with cavities and overcame this problem, but he appears to have done so by presuming that the basic theory is correct and inventing a specific function (equation 3.7 and Figure 4 in Reference FowlerFowler, 2009) to make it happen. This stopped the effective pressure dropping to zero (i.e. the condition of cavitation), which is the equivalent of letting ‘just enough’ weak till squeeze into places where it needs to be to prevent the development of bed separation.

Three-dimensional instability modelling and where are the drumlins?

Frustratingly, the Hindmarsh-Fowler instability theory has no problem generating ribs – in fact it nearly always does – but it never seems to make truly 3-D forms resembling drumlins. Further theoretical development by both Hindmarsh, and Reference FowlerFowler (2010a) included adding the upper ice surface (ice-air). Prior to this, for convenience, modelling had proceeded with an infinite ice thickness. In Fowler’s analysis, the addition of this extra aspect, while making the model more physically realistic, failed to generate lateral instabilities. In Hindmarsh’s case, and using a newly developed 3-D analysis, some lateral instabilities emerged in some model runs (in the both the till-ice and ice-air surface), but it has yet to be ascertained whether they are real or numerical aberrations.

In order to see if drumlin-type lateral instabilities might spontaneously arise, it was necessary to extend the 2-D (flowline) case to be fully 3-D (Chapwanya and others, in press). Numerical solutions of the model were constructed with meltwater evacuated through the till by a passive drainage rule; it simply gets to where it needs to be, governed by hydraulic potentials. A set of model experiments was executed starting with a ‘flat’ till surface. With no prompting other than that provided by the theoretical foundations of the instability theory, ribs rapidly arose, slowly migrating downstream, with appropriate spacing and comprising imperfections and dislocations that make them resemble aspects of real ribbed moraine (Fig. 10). Numerous model runs were executed and viewed as movie animations, carefully searching for the appearance of drumlin-like phenomena. Based on the frequently observed downstream transitions from ribbed moraine, to ribbed moraine with superimposed drumlins, to just drumlins (e.g. Fig. 1 and Reference AarioAario, 1977), the expectation was that after enough time, drumlin-like shapes would appear in model runs. Unfortunately, clear cases failed to appear. As Figure 10 demonstrates, there are some minor elongated culminations that do arise, but it is uncertain whether this is a major achievement (i.e. modelled drumlins) or whether they are just some ridge summits and perhaps arise from numerical problems. Chapwanya and others (in press) took the more cautious view and concluded that while ribbed moraine is likely well explained by the theory so far, an extra ingredient is probably required before drumlins can be produced. A more optimistic view is that drumlins have been generated by the model and that it is actually unusual for drumlins to appear beyond ribbed moraine. In Ireland, for example, we now know that the famous drumlin belt (Fig. 2) is actually better described as ribbed moraine with some superimposed drumlins (Reference Knight and McCabeKnight and McCabe, 1997;Reference Clark and MeehanClark and Meehan, 2001). Maybe ribbing always underpins drumlins and we have yet to notice this properly.

Fig. 10. Modelled subglacial bedforms using the Hindmarsh–Fowler instability theory as formulated by Chapwanya and others (in press). From a flat till base of 6 km × 6 km domain and with an ice velocity of 100ma–¹ the landforms depicted here grew to ~0.7m high in a simulated 50 years. Ice flow from left to right and with red as high elevations through to blue as low. As expected, the instability generated ribs at the appropriate wavelength, with dislocations and plan curvatures resembling real ribbed moraine. Drumlin-like culminations (red) appear on the ridges, but the expected evolution from such drumlinized ribs to just drumlins was not achieved in the model runs.

If drumlins are difficult to generate by purely lateral instabilities in the coupled flow of ice and sediment, the next step may be to include a better treatment of meltwater flow. When water encounters a stiff ridge orthogonal to its flow direction (a rib), it is natural to expect it to attempt to breach it. Can this help make drumlins? If water flow can be sensibly modelled along with the instability theory, then drumlins may emerge. Fowler (2010b) has presented a model which has a dynamic description of localized water flow in a primitive drainage system (i.e. no channel dynamics). The model shows that a uniform water film between ice and a deforming bed is inherently unstable and breaks down into subglacial streams in a manner analogous to how subaerial overland water flow is unstable and breaks down into rills (i.e. the Reference Smith and BrethertonSmith and Bretherton (1972) rilling instability). The effect of the overlying ice is that it dampens the spatial frequency of the rilling, yielding stream spacings at a scale compatible with mega-scale glacial lineations (Reference ClarkClark, 1993). The implication is that perhaps the corrugations that comprise MSGL are created by sediment removal by subglacial meltwater in steady streams (not floods, in case you are wondering). In the choice of parameter values and the model formulation to produce such rilling of MSGL, the ribbing instability was not enabled;it would have likely dominated, producing ribbed moraine rather than MSGL. Further theoretical developments may allow the ribbing and rilling instabilities to be run together. With such a model, perhaps the evolving land surface will take many forms including those of ribbed moraine, drumlins, MSGL, transitions between them and yet-to-be-named strange subglacial bedforms that nature exhibits.

Till rheology

The instability theory is intimately associated with, and perhaps tainted by, the debate surrounding till rheology and flow laws (e.g. Reference HindmarshHindmarsh, 1997;Reference MurrayMurray, 1997;Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000;Reference Iverson and IversonIverson and Iverson, 2001; Reference FowlerFowler 2003; Reference ClarkeClarke, 2005). Early versions of the theory used a viscous rheology, and instabilities were found to exist (Hindmarsh 1998b). However, once it became clear that such a viscous rheology might not be appropriate (e.g. reviewed in Reference ClarkeClarke, 2005, and see Reference IversonIverson, 2010), analysis was performed by Reference SchoofSchoof (2007), Hindmarsh (in Reference Dunlop, Clark and HindmarshDunlop and others, 2008) and Reference FowlerFowler (2009), all concluding that the presence of unstable states was not dependent on the choice of rheology (from viscous to plastic). All that is required by the theory is that there is basal ice motion and a mobile till and that their movement depend sensibly on both basal shear stress and the effective pressure at the ice-till surface (Reference FowlerFowler, 2009). Till rheology is thus best regarded as a perceived rather than real problem for the theory.

Internal sedimentary properties and architecture

The instability theory tends to appeal to geomorphologists because they naturally focus on bedform shape and patterning in a field and the theory appears to explain these well. However, glacial geologists who have investigated the sedimentological properties and internal architecture of drumlins or ribbed moraine tend to find the theory unsatisfactory because it does not seem to explain their observations. This might be because it appears to imply that all sediments should be highly deformed and mixed up. The latter group have sometimes used their observations of complexity and multiphase sediment build-up, for example, to argue against the theory, which is premature for the following reasons.

Firstly, the theory insofar as it has thus far been advanced, has little to say or predict regarding the sedimentological properties of bedforms. There is an unfortunate scale disparity between a rather abstract theory and detailed field observations. Till mobility is modelled, but as a homogeneous material and not at the grain-to-grain scale of interaction. In principle, one could imagine building new components to the theory that attempt to bridge this scale gap. At the simplest level, sedimentary layers of different rheologies could be included and the disposition of these layers traced as bedforming progresses. This is probably tractable and may provide broad indications of what the geological record should look like, but it is likely to be inadequate judged against the observed complexities in sections, which probably arise from very specific situations arising from sediment inhomogeneities, grain-to-grain interactions and polyphase deformations, etc. Modelling to predict such a detail is probably impossible at present, especially since the nature of till as such a highly variable medium would make it difficult to proceed. Also, any dependence on initial conditions (what were the sediment properties prior to bedforming) could make such modelling exercises fruitless.

Secondly, all the theory says, thus far, is that the upper till surface becomes unstable and wavy. All manner of sedimentary structures, for example, could be generated or preserved beneath this surface (Figs 11 and 12). A thickening till layer would yield drumlins or ribs mostly with deformed sediment within them and which might or might not leave a visible sedimentary signature recording the deformation. A lowering ice-till surface could yield bumps containing stratified sediments, eroded in places by the mobile layer (see Reference HartHart, 1995). This is the interpretation that Reference Boyce and EylesBoyce and Eyles (1991) made for the Peterborough drumlin field in Canada, when presented with drumlins cut into horizontally bedded sands and gravels with a thin drape of till, and is imagined as ‘drumlins carved by deforming till streams’ (Boyce and Eyles, p. 787) and schematically illustrated earlier (Fig. 3). In Figure 12 we note that just because a sedimentary structure is found within a drumlin, it does not imply it was relevant to the process of drumlinization. We also speculate that flutes which are much smaller than drumlins might also be generated by instability in the coupled flow of ice and sediment (Fig. 12b), although modelling has yet to be performed to see if the wavelengths and amplitude are appropriate (see Reference Schoof and ClarkeSchoof and Clarke, 2008).

Fig. 11. The instability theory predicts that the ice–till interface, under certain circumstances, is unstable and becomes wavy. If we start with a simple stratification of deposits (a), say till on gravel on sand, and if the instability operates with a greater volume of sediment advected into the region than out, then the deforming layer will thicken (b), yielding bumps mostly comprising sheared till. Alternatively, more sediment might be leaving than entering, in which case the wavy surface will evolve downwards (c, d), with the mobile sediment eroding into lower units. Stratified sediments might thus be preserved within the bumps. The upper layer of deforming sediments might be preserved (solid to dashed line) or be removed by erosion. Reference HartHart (1995, Reference Hart1997) discusses these scenarios and describes (b) as constructional and (c) and (d) as destructional deformation. These are sketches, not model output, and no scale is implied other than that bump spacing (either ribbed moraine or drumlins) should be of the order of hundreds of metres.

Fig. 12. (a) If pre-existing sediment contained structures, say thrusts or folds, these could be preserved in drumlin cores even though they have no process relationship to the drumlinization. (b) Flutes are much smaller landforms (tens of metres) than drumlins, and their common positioning in the lee of lodged boulders is usually taken to imply that they form by sediment migration into a pressure-lee or cavity behind the boulder (Reference BoultonBoulton, 1976). An alternative is that they might be formed by flow instabilities whereby a thinning (by advection) till sheet with an unstable wavy surface becomes ‘anchored’ on boulders when they are encountered. If true, this helps explain the numerous flutes that are observed without boulders, without having to invoke subsequent boulder theft. In this sketch, ice flows out of the page.

Thirdly, the theory has so far only addressed emergent drumlins, just one of the three possible types (emergent, obstacle and clone);the others should have different internal architectures.

There may be an unfortunate bias in the reporting of observations regarding internal properties of subglacial bedforms. If a large number of sections are observed and sedimentological and structural properties are found to be complex and interesting in some of them, then clearly these examples would make an interesting paper. In sections where only fairly homogeneous till is apparent, with no appealing phenomena, then we suspect such cases tend to go unreported, because they make a less interesting paper in relation to their more exotic cousins. This might mean that our sample of what the interior of bedforms looks like (judged from the literature) is not representative of the wider population and, by focusing on the complex cases, makes the task of finding the drumlin process more difficult than it needs to be. In a wide survey of drumlin internal structures, Reference HartHart (1997) reported on the internal structure of around 50 drumlins, finding that the erosional type (e.g. Fig 11c and d) was by far the most common in the sample. We suppose that geophysical survey of whole drumlin fields, with random sampling via cut sections or cores, could reveal what bed- form interiors are usually like and what a theory should aim to mostly explain. The refinements could then come later.

For palaeo-ice sheets it is now well known that ice-flow directions varied as a consequence of ice-divide migrations and the activity of ice streams, yielding cross-cutting and palimpsest final bedforms (e.g. Reference ClarkClark, 1993; Reference Kleman, Hattestrand, Borgstrom and StroevenKleman and others 1997). If we consider a bedform field shaped under a specific ice-flow direction and then modified by flow from a different source, it is easy to imagine that complex and polyphase signatures could be generated in the sedimentary record. Perhaps some of this has added to the difficulty of trying to work backwards from the geological signature to infer the process of bedforming.

Irrespective of the above points, a good theory of drumlin formation clearly must not be contradicted by the characteristics of sediments and associated structures (thrusts, bedding, folds, etc.) found within them. However, ‘the problem of choosing the significant and avoiding the irrelevant is very difficult’ (Reference Smalley and UnwinSmalley and Unwin, 1968, p. 377). The key question when making sedimentological observations within sections through drumlins must surely be: which observations (say, folds) and inferred processes (compressional deformation) relate to the actual phase of drumlin building (i.e. that makes the drumlin shape, not just the body of sediment)? It might be, for example, that some observed phenomena (e.g. thrust structures) pre- or post-date drumlin building and are thus not relevant (Fig. 12a). Finding unequivocal process-form relationships between sediment structures within a drumlin and the overall size and shape that defines the drumlin is, however, often difficult. It is a problem that needs careful analysis. In the instability theory, it has been shown that the instability can determine the wavelength (many hundreds of metres scale) and amplitude of bumps and, although not yet specified by modelling, it is supposed that at the finer scale seen in sections (tens to hundreds of metres), mobility of the deforming sediments may be manifested by a variety of mechanisms including pervasive shearing, movement along thrust planes or by folding, squeezing of more mobile sediment into cavities, etc. Relating the instability mechanism with the observed sedimentary products remains a challenging task.

The dreaded, but largely semantic, problem of equifinality

Equifinality is the principle that a given end state (i.e. a specific landform) can be reached by many different mechanisms, and is both a serious potential problem but also a convenient arguing-tool with which to attack theories. At its most absurd, if a group of researchers cannot agree how a phenomenon arises, or which theory is correct (or best), then, if in a conciliatory and democratic mood, they might conclude that they all work and the phenomenon can be generated by a whole host of widely different means. Nature might not work like this, however. In subglacial bedform research, this friction is acute because we have named a whole host of seemingly related phenomena (flutes, drumlins, ribbed moraine, mega-scale glacial lineations, crag and tails, etc.), based on what they look like. Such a genesis-blind classification is understandable until we know better. There is no requirement on the instability (or any other) theory to predict all streamlined bumps or subglacial transverse ridges, if our crude (genesis-blind) classifications of bedforms have inadvertently included some landforms that were created by a different means and should therefore be sensibly renamed (once we know this!).

There appear to be two approaches to the problem, different in which bedform characteristics primarily motivate them. Investigation of the internal properties of specific drumlins and ribbed moraine finds that they often look different, and by building backwards from properties to process this often implies that they formed by different mechanisms. We could thus have dozens of different mechanisms for drumlins and ribbed-moraine generation, and if all were found to be true this would sensibly require a renaming of the phenomena, for example as thrust-stacked ribbed moraine (Reference BouchardBouchard, 1989), till-fractured ribbed moraine (Reference Kleman and HattestrandKleman and Hattestrand, 1999) flood drumlins (Reference ShawShaw, 2002), dilatancy drumlins (Reference Smalley and UnwinSmalley and Unwin, 1968), lee-side cavity drumlins (Reference Dardis, McCabe and MitchellDardis and others 1984), etc. Using properties to build theories tends to take us down this route, and if appropriate we should finally find the subspecies of drumlins and ribbed moraine. Or if we do not wish to rename features, we could regard ribbed moraine, for example, as polygenetic landforms as argued by Reference LundqvistLundqvist (1997), Reference Linden, Moller and AdrielssonMoller, (2006) and Reference Linden, Moller and AdrielssonLinden and others (2008). The quest here would be to try to relate mechanisms implied by the sedimentological observations with the morphological properties of the landforms. This will be impossible if pure equifinality holds, but there may be some breakdown in equifinality such that process-X drumlins do look slightly different to process-Y drumlins. Alternatively, and very much inspired by remote-sensing views of bedforms (e.g. Figs 1 and 2) where we see the phenomena expressed as regular and patterned bumpiness across wide areas, with transitions between differently shaped and arranged bumps, the tendency is to infer a single unifying process that manifests itself differently (i.e. a true bedforming rather than specific landform view). Maybe the variations in shape, arrangement and internal properties arise from different conditions (ice thickness, velocity, pore- water pressure) and histories (maybe ribbing followed by a change in ice thickness and flow direction, yielding barchan forms eventually becoming drumlins). A unifying theory might thus explain most of the bedforms by one basic mechanism, apart from perhaps some different landforms mistakenly classified into the group. Using the latter to attempt to falsify the former is of course unproductive and becomes largely an exercise in naming things.

The idea, earlier expressed, of self-organization by a process to generate ‘true or usual’ emergent drumlins, and that can also explain drumlin clones (erosional shaping of stiff patches of sediment) or obstacle drumlins (agglomeration around a bedrock knob), acknowledges some element of equifinality but appeals to one basic process: mobile till being unstable and the surface becoming wavy. With a homogeneous substrate this would be all that arises, but where we have imperfections (pre-existing sedimentary or bedrock inhomogeneities) these can become anchors and fix an instability element in place (Fig. 12b).