Introduction
Johan Dahl Land in south Greenland was chosen in 1975 as a possible site of a hydropower station, and hydrological measurements were started there in 1976 by the Greenland Technical Organization. As the basin contains an outlet from the Greenland ice sheet, glaciological measurements were also made over six summers 1978–83 by the Geological Survey of Greenland. For reasons unrelated to the physical conditions in Johan Dahl Land, plans for hydropower were shelved in 1983, although they could be taken up again in connection with future mining operations.
The glaciological work in Johan Dahl Land was started with the intention of applying standard glaciological and hydrological methods but, in the event, some concepts need modification for Greenland conditions. In particular, it is very difficult to determine areas of drainage basins on the Greenland ice sheet. The reason is that liquid water at any point on the ice sheet does not necessarily flow in the same direction as the ice flow. This is equivalent to having separate “basins” for liquid and solid water, i.e. hydrological and glaciological basins, respectively, although water on the surface does not necessarily flow in the same direction as englacial and subglacial water. The problem is further complicated because surface topography on the ice sheet is poorly mapped and there is little information about subglacial topography. The Geological Survey of Greenland is actively researching these problems, while the present paper attempts to assess the effects of glaciers on run-off in Johan Dahl Land without accurately knowing the drainage area.
Physical Setting
Johan Dahl Land is an upland area located about 25 km north of Narssarssuaq in south Greenland (Fig. 1). The area is uninhabited and seldom visited except for back-packers and scientisists.
The proposed hydropower station would have used a large lake (Nordbosø with an area of 11 km2) as a reservoir, and water from a smaller lake (Thor Sø with an area of 5 km2 would have been piped into this reservoir. The Thor Sø basin is ice-free and is therefore a pure precipitation basin. By contrast, the Nordbosø basin includes small isolated glaciers and a tongue of the Greenland ice sheet (Nordbogletscher). Its run-off is therefore influenced by glacier ablation as well as by precipitation.
Climate
The climate of Johan Dahl Land is Arctic as monthly mean temperatures are always below 10° C. For example, temperatures are only above freezing for about 4 months in the year, i.e. from mid-May to mid-September, For the rest of the time, the area is covered with snow although, even in winter, there can be short sudden spells of warm weather with melting caused by Föhn-type storms. The longest climate record in the area is from Narssarssuaq which is an airport established in 1941. Climatological measurements were made at a station alongside Nordbogletscher for the six summers 1978–83 (Oleson, 1978; Reference ClementClement 1981, 1982, 1983, 1984[a]) as part of the glaciological research programme. Monthly mean temperature and monthly precipitation total at this station have reasonably high correlations with the corresponding values at Narssarssuaq (Reference ClementClement, 1984[a]). Although there are no climatológical data from the Thor Sø basin, there are no grounds a priori to suspect that its climate is greatly different from the lowest part of the Nordbosø basin.

Fig. 1. Johan Dahl Land, south Greenland, showing locations of the Nordbosø and Thor Sø basins.
Basin Characteristics
The Thor Sø basin covers an area of 32 km2 and is ice-free. The areas of ice-free land (including lakes) and small glaciers in the Nordbosø basin are 96 and 5 km2 respectively. The terrain is very rugged and sparsely vegetated, with elevations ranging from 660 m a.s.l. at the lake Nordbosø to 1650 m a.s.l. at Valhaltinde.
The total area of the Nordbosø basin is uncertain because the area of Nordbogletscher from which liquid water drains into the Nordbosø lake is problematic. Reference OlesenOlesen (1978) stated that Nordbogletscher is a “branch” of the glacier Eqalorutsit kangigdlit sermiat with an area of 35 km2 within the perimeters of the Nordbosø hydrological basin. The delineation of Nordbogletscher was extended on to the ice sheet to give a total area of 208 km2 during the course of the glaciological investigations by Reference OlesenOlesen (1978) and Reference ClementClement (1981, 1982, 1983, 1984[a], [b]). However, it was gradually realized that this represents the glaciological area of Nordbogletscher; the area from which liquid water flows to Nordbosø must be much smaller. For example, Reference ClementClement (1984[a]) gave an area of 57 km2 for this hydrological basin. The area estimates of Reference OlesenOlesen (1978) and Reference ClementClement (1984[a]) are equivalent to a glacier cover of 29–39% of Nordbosø basin with a total area of 136–158 km2.
Using the above area, the Nordbosø basin has only 7–8% of lake cover compared with 17% for the Thor Sø basin.
The Data
The data used in the present study are annual run-off from Nordbosø and from Thor Sø, annual precipitation at Narssarssuaq, and annual ice ablation on the tongue of Nordbogletscher, which are summarized in Table I.
Annual Run-Off
Run-off from Nordbosø and Thor Sø have been determined since 1976 and 1978, respectively, by the Greenland Technical Organization. The data in Table I are the latest results from GTO (1986[b]) and refer to annual run-off for the year 1 January–31 December.
The run-off values are based upon continuous recording of water level in the main lakes Nordbosø and Thor Sø, respectively, which are transformed to run-off volumes by use of rating curves for the corresponding outlet streams. The rating curves themselves are based upon many spot measurements of discharge versus water level. Under Greenland conditions, such measurements are laborious and it usually takes several seasons to achieve a satisfactory rating curve. This means that run-off values from Greenland are subject to amendment as the rating curve is updated. However, the data from Nordbosø and Thor Sø both appear to have reached the stage where the rating curve is little changed by the addition of extra measurements. The calculations in Reference BraithwaiteBraithwaite (1985) are based on an older data set which has been slightly updated to that shown in Table I of this paper.

Table I. Summary of hydrological conditions in johan dahl land, south greenland 1976–85. q 1 is annual run-off of nordbosØ basin, q 2, is annual run-off of thor sØ basin, p is annual precipitation in narssarssuaq, and a is annual ice ablation on the tongue of nordbogletscher
There are times when the recording instruments break down so that missing water-level values must be filled in by estimation. This is done as part of the data analysis by the GTO (1986[b]) and the figures in brackets in Table I give percentages of the annual run-off accounted for by estimated rather than measured water-level values. With the exception of 1978, the 1978–83 record for Nordbosø is almost complete, while there are substantial periods of missing records for Thor Sø in 4 out of 6 years of interest. Run-off from Thor Sø is probably less accurate than run-off from Nordbosø.
Annual Precipitation
Precipitation is measured at Narssarssuaq, about 25 km south of the Nordbosø and Thor Sø basins, by the Danish Meteorological Institute. The data in Table I refer to annual precipitation for the hydrological year 1 September–31 August. Precipitation in September-December is assumed to fall mainly as snow and to contribute to run-off in the calendar year 1 January–31 December. This cannot be exactly true as Föhn storms can cause strong melting of snow at any time. For convenience in calculating annual precipitation from monthly totals, the hydrological year is assumed to be of fixed duration and to include only complete months. However, more correctly the hydrological year is of irregular duration starting in early or mid-September. Despite these simplifications, the plot in Figure 2 indicates that the present choice of hydrological year is not unreasonable, especially as some of the indicated run-off in September may be drawn from lake storage rather than being provided by precipitation.

Fig. 2. Seasonal variations of run-off from Nordbosø. Thor Sø, and precipitation at Narssarssuaq. Data are expressed as cumulative percentages of their respective monthly averages for 1978–83.
Annual Ice Ablation
Snow accumulation and ice ablation were measured for the six summers 1978–83 at many stakes on the tongue of Nordbogletscher by Reference OlesenOlesen (1978) and Reference ClementClement (1981, 1982, 1983, 1984[a]). In this paper, ablation is taken to be positive, instead of negative as in Anonymous (1969), as this seems more logical for hydrological purposes. The ablation values given in Table I are averages of measurements from 14 stakes which were maintained throughout the 6 years of measurements (the mean elevation for the 14 stakes is about 870 m a.s.l.). According to Reference BraithwaiteBraithwaite (1985), the year-to-year variations of annual balance at these stakes represent about three-quarters of the total variance (for 14 stakes and 6 years) with errors accounting for a further 18% of variance. As the stakes were located in the lower ablation area, the ice ablation is essentially identical to annual balance (measurement year from early September to early September) with its sign reversed, and is also comparable with the “Eis-Nettoablation” in Reference AmbachAmbach (1972).
Run-Off Variations
Run-off from Thor Sø is caused by rainfall and snow melt, while run-off from Nordbosø is supplemented by ice melt. Assuming uniform precipitation variations in the area, differences in run-off between the two basins reflect effects of glaciers on run-off. On the other hand, differences between run-off from Thor Sø and precipitation at Narssarssuaq reflect the effects of snow accumulation and melt. This simple picture could be partly obscured by effects of errors in the data, e.g. measurements of solid precipitation are notoriously inaccurate.
Seasonal Variations
Seasonal variations of run-off from the two basins and of Narssarssuaq precipitation are compared in Figure 2. Means of monthly totals of the three series are plotted as cumulative percentages of their respective mean annual values for 1978–83. The curve for Narssarssuaq precipitation is fairly straight, indicating that precipitation rate is roughly constant throughout the year, although there is slightly higher precipitation for June–October.
The run-off curves for Nordbosø and Thor Sø follow each other quite closely and are very different from the precipitation curve. This shows that water-storage changes are important for the annual hydrological cycle while the contribution of ice melt is less important.
The curves in Figure 2 show that the effect of glaciers on run-off is relatively small in Johan Dahl Land on a seasonal basis. However, there are some interesting differences between the two run-off curves. For example, run-off from Nordbosø in August and September is proportionally higher than run-off from Thor Sø as well as higher than precipitation. This is probably a glacier effect whereby the extra run-off from Nordbosø is provided by melting ice, while the run-off from Thor Sø is essentially the same as precipitation as all snow has been melted away. From October until April, the two run-off curves are parallel and their lower gradients compared with the precipitation curve indicate that most precipitation in this period falls as snow and does not contribute to run-off. Both curves start to rise in May, indicating the onset of melting. However, Thor Sø run-off rises faster than Nordbosø run-off in May and June, partly reflecting the lower average elevation of the Thor Sø basin, which will therefore be warmer, but another important factor is an ice-dammed lake in the Nordbosø basin (Reference ClementClement, 1984[b]) which fills up in May and June and thus reduces run-off from Nordbosø. This lake starts to drain in early to middle July, thus causing the Nordbosø run-off curve to rise faster than the Thor Sø curve for July and August.
The difference in seasonal run-off patterns between glacier-free and glacier-covered basins, e.g. the delay in run-off from a glacierized basin (Reference MeierMeier, 1969; Reference Fountain and TangbornFountain and Tangborn, 1985), probably increases with increasing glacier cover. The fairly small differences in seasonal run-off between Nordbosø and Thor Sø are therefore consistent with a small to moderate amount of glacier cover in the Nordbosø basin.
Year-to-Year Variations
Annual values of run-off from the two basins and of Narssarssuaq precipitation are plotted in Figure 3. The data are expressed as percentage deviations from their respective mean annual values for 1978–85.
In contrast to the seasonal variations, there is closest agreement between Narssarssuaq precipitation and Thor Sø run-off, while the run-off from Nordbosø follows a different pattern. However, there is one year (1979) with a large difference between the first two series, possibly due to errors in estimating missing data for that year.
In order to examine the above patterns, correlation coefficients were calculated between the two annual run-off series and the precipitation and ablation series in Table 1. The results are given in Table II where all correlations refer to the 6 year period 1978–83. The run-off from Nordbosø and from Thor Sø have similar correlations with annual precipitation p, i.e. correlation coefficients of +0.77 and +0.72, respectively, which indicate moderately large correlations. The correlation between the two run-off series is even higher (R - 0.93). However, as already seen in Table I, the run-off from Nordboso is proportionally less variable than the run-off from Thor Sø, e.g. the standard deviations of the two series constitute ±13% and ±36% of their respective mean values. Run-off from the Nordboso basin therefore follows the variations of Thor Sø run-off and Narssarssuaq precipitation with reduced amplitude.

Fig. 3. Annual departure from mean of run-off from Nordbosø, Thor Sø. and precipitation in Narssarssuaq. Data are expressed as percentage deviations from their respective averages for 1978–83.
From the foregoing it is clear that the major effect of glaciers in this case is on the year-to-year variations of run-off rather than on seasonal variations. The hydrological effect of glaciers in Johan Dahl Land is therefore to smooth year-to-year variations in run-off as in other areas, e.g. western North America (Reference MeierMeier, 1969; Reference Krimmel and TangbornKrimmel and Tangborn, 1974; Reference Fountain and TangbornFountain and Tangborn, 1985), Scandinavia (Reference Tvede and TvedeTvede, 1983), the Alps (Reference KasserKasser, 1959; Reference CollinsCollins, 1985; Reference Röthlisberger, Lang, Gurnell and ClarkRöthlisberger and Lang, 1987), Pakistan (Reference FergusonFerguson, 1985), and China (Reference LaiLai Zuming, 1982; Reference YanYang Zhenniang, 1982). The possible mechanisms of this effect are examined later.
Long-Term Variations
Measurements were only started in 1976, so the question of long-term variations in annual run-off is speculative. However, a possible source of such variations is change in volume of Nordbogletscher as the tongue has been advancing steadily since at least 1942. According to Reference ClementClement (1984(a]), the total advance into the lake Nordbosø in the period 1942–81 is 0.4 km2. Assuming an ablation rate of about 3 m a1 at the tongue of Nordbogletscher, the total increase in annual run-off due to increased tongue area over the 40 year period is 1.2 × 106 m3 a−1. This figure should be increased for expansion of Nordbogletscher along its flanks, but the increase in run-off is still small compared with the 1978–83 average of 174 × 106 m3 a−1. given in Table I. Long-term changes in run-off due to the advance of Nordbogletscher are therefore neglected compared with seasonal and annual run-off variations.

Table II. Correlation coefficients between annual run-off from nordbosØ, q 1, annual run-off from thor sØ, q 2, precipitation in narssarssuaq p, and ablation a on nordbogletscher for the 6 years 1978–83
Annual Run-off Model
In the following, changes in annual storage of liquid water in ground water and in lakes as well as in the subglacial and englacial systems are ignored. Run-off can come from rainfall, ablation of glacier ice, ablation of snow from the current hydrological year, and ablation of firn stored in perennial snow patches and in the accumulation area of glaciers. It is convenient to re-group these different terms so that annual precipitation appears in the water-balance equation. The annual precipitation is divided between rainfall and snow accumulation where the latter contributes to snow ablation and to the accumulation of firn and superimposed ice which are stored into the following hydrological year. The appropriate ablation term to use together with annual precipitation is therefore the net ablation, which comprises the ablation of ice and of firn minus the accumulation of firn and superimposed ice (snow ablation is included under annual precipitation). Defined in this way, the net ablation represents the net loss from the glacier surface over the hydrological year and is essentially the annual mass balance b a (Anonymous, 1969) with its sign changed.
Consider a basin of area F of which an area G is covered by glaciers. The glacier cover α = G/F. The annual specific run-off in the year t is q t which is given by:
where p t is the annual precipitation averaged over the whole basin, a t is the net ablation at the glacier surface averaged over the glacier cover within the basin, and e t is the annual evaporation averaged over the glacier-free area with evaporation from the glacier assumed to be zero.
As it stands, Equation (1) is reasonably general and applies to both basins containing self-contained glaciers and those containing sectors of the ice sheet. However, in the former case the net ablation a t refers to whole glaciers, while in the latter case it refers only to the parts of glaciers within the hydrological basin. In the particular case of Johan Dahl Land, the upper boundary of the Nordbosø hydrological basin, according to both Reference OlesenOlesen (1978) and Reference ClementClement (1984[a]), lies below the average equilibrium line, so there is little accumulation of firn or superimposed ice at the end of the hydrological year and the net ablation is the same as ice ablation measured by stakes drilled into the glacier surface.
In principle, the glacier cover α changes as glaciers advance and retreat but in the present case it is known that Nordbogletscher has advanced very little during the period of record compared with the uncertainty in α itself. More subtly, α could change on a seasonal or year-to-year basis if shifts in the internal hydraulics of glacier sectors cause changes in the boundaries of hydrological basins. This possibility cannot be included in the present treatment but is being investigated by new field work. The following treatment also assumes stationary climatic conditions. Whether or not this is exactly true, it is certain that any climatic trend is small compared with seasonal and year-to-year variations.
Standard Deviation
The average annual run-off 〈q〉 for an N year period is given by:

and the deviation of run-off from this average in the year t is given by:
Averages and deviations are defined in similar ways for annual precipitation, net ablation, and annual evaporation. Neglecting evaporation deviations compared with precipitation deviations gives:
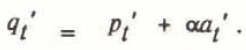
By definition, the run-off variance for an N year period is given by:

where S q is the standard deviation of the annual run-off. Squaring both sides of Equation (4) and averaging over N years gives the run-off variance as:
where S p and S a are the standard deviations of annual precipitation and net ablation respectively, and R pa is the correlation coefficient between precipitation and ablation defined by:

According to Equation (6), if R pa is zero, i.e. if net ablation is not correlated with precipitation, the variance of the annual run-off is simply equal to the sum of the variances of precipitation and ablation. However, in the present case R pa is negative with a correlation coefficient of −0.63 so that the variance of the annual run-off is less than this sum, i.e. the negative correlation between precipitation and ablation smooths year-to-year variations in annual run-off, depending upon the glacier cover α.
The negative correlation between ablation and precipitation arises because increased precipitation is associated with increased accumulation of snow during the winter and the melting of this uses energy in the summer which would otherwise be available for melting ice. This effect is accentuated by the fact that a certain amount of snow accumulation inhibits a greater amount of ice melt (Braithwaite and Olesen, in press). Increased ablation therefore reduces ice ablation.
Using Equation (6) and the results in Tables I and II (S p= 0.18, S a = 0.53, and R pa = −0.63), together with a glacier cover α of 0.30−0.39, gives a range of 0.15−0.17 m water for the standard deviation of specific run-off from Nordboss. With a basin area of 135–157 km2, the corresponding standard deviation of run-off volume is 20–27 × 106 m3 a−1, which is in good agreement with the value of 23 × 106 m3 a−1, for observed run-off volume for Nordbosø. On the other hand, according to Equation (6), the specific run-off from a glacier-free basin should have the same standard deviation as precipitation. This assumption gives a standard deviation of 6 × 106 m3 a−1 for the volumetric runoff compared with the observed value of 8 × 106 m3 a−1 for Thor Sø, i.e. the model underestimates by about 25%.
In order to apply the results to other basins, the variation of standard deviation is plotted in Figure 4 as a function of a using data from Johan Dahl Land. As before, S p = 0.18 and R pa = −0.63, but it is more difficult to choose a general value for S a because the available ablation data from Nordbogletscher refer to the lowest part of the glacier. Basins with higher-lying glaciers have lower ablation and S a might be lower in proportion. Values of the ratio S a/S p equal to 1 and 2, as well as 3 for the present case, are therefore assumed to cover the range of likely S a values.
Minimum Standard Deviation
The plots in Figure 4 predict that increasing glacier cover reduces the standard deviation of annual run-off down to a certain minimum after which it increases again, possibly to a very large value if ablation has a high variabilty. By differentiation of S q in Equation (6) with respect to α and setting the derivative dS q /dα equal to zero, the glacier cover α1 giving the minimum standard deviation is found to be:


Fig. 4. The standard deviation of annual run-off. Johan Dahl Land, calculated as a function of percentage of glacier cover. The three curves refer to values of 1, 2, and 3 for the parameter Sa/Sp.
With the present values, α1 = 0.21 but this minimum is shifted towards higher values of glacier cover with decreasing variability of ablation relative to precipitation, i.e. by decrease in S a/S p .This can be compared with 0.3 in Reference Krimmel and TangbornKrimmel and Tangborn (1974), 0.36 in Reference Fountain and TangbornFountain and Tangborn (1985), 0.20 in Reference Tvede and TvedeTvede (1983), 0.3–0.4 in Reference KasserKasser (1959), 0.3–0.6 in Reference Röthlisberger, Lang, Gurnell and ClarkRöthlisberger and Lang (1987), and 0.1–0.2 in Reference FergusonFerguson (1985).
The minima in the curves in Figure 4 look rather shallow compared with similar curves from other regions (personal communication from M.F. Meier). Substitution of α1 from Equation (8) back into Equation (6) gives the minimum standard deviation as S p(1 – R pa 2)0.5. This means that the depth of the minimum in the curve of standard deviation versus glacier cover is controlled by the correlation between precipitation and ablation. In the present case, R pa = −0.63, so that the minimum standard deviation is 0.78S p which represents a fairly shallow minimum. The deeper minimum found in other areas, e.g. as shown in figure 10.4 in Reference Röthlisberger, Lang, Gurnell and ClarkRöthlisberger and Lang (1987), suggests that R pa may be more negative than found here. It is also possible that the value R pa = −0.63, based upon ablation data from the lowest part of the glacier, is an underestimate of the correlation for basins containing whole glaciers.
As a low standard deviation of annual run-off is desirable for water management, the most attractive basins for exploration are ideally those with a moderate amount of glacier cover.
Run-off with Precipitation Correlation
The correlation between annual run-off q t and net ablation p t is R qp given by:
which is obtained by multiplying both sides of Equation (4) by the ablation deviation p t ′, averaging over an N year period, and applying the definitions in Equations (5) and (7).
The dependence of the run-off with precipitation correlation on glacier cover is plotted in Figure 5 for the same assumptions as for Figure 4. Naturally, the equation refers to an “ideal” correlation in the absence of errors which generally reduce correlations calculated for real data. However, the equation predicts that the highest correlation between run-off and precipitation occurs for glacier-free basins and that the correlation decreases with increasing glacier cover. The correlations given in Table II do not exactly agree with this as run-off from Nordboss has a slightly higher correlation with precipitation than does run-off from Thor Sø i.e. correlation coefficients of 0.77 and 0.72, respectively. This might partly reflect the effects of proportionally larger errors in the Thor Sø data but the run-off with precipitation correlation from Nordbosø is also higher than that predicted by Equation (9). For example, present results (S p = 0.18, S a = 0.53, R pa= −0.63, and α = 0.30−0.39) give a calculated run-off with precipitation correlation of only 0.30−0.54. This theoretical correlation could be increased according to Figure 5 by either decreasing the glacier cover or by reducing S a, compared with S p.

Fig. 5. The correlation coefficient between annual run-off and precipitation, Johan Dahl Land, calculated as a function of percentage of glacier cover. The three curves refer to values of 1, 2, and 3 for the parameter Sa /Sp.
The run-off with precipitation correlation offers a basis for forecasting run-off. For example, if most of the precipitation occurs in the winter while most of the run-off occurs in summer, forecasts of summer run-off can be made at the start of the melt season. This is of economic benefit for water management. However, according to Equation (9), run-off is less sensitive to fluctuations of precipitation for basins with greater glacier cover because the higher (or lower) run-off from the glacier-free parts of basins is largely offset by lower (or higher) run-off from the glacier parts. This means that it is more difficult to forecast summer run-off in glacierized basins than in snow-covered basins without glacier cover as pointed out by Reference MeierMeier (1969) and Reference FergusonFerguson (1985), among others. According to Figure 5, the correlation coefficient between run-off and precipitation may even cross zero and become negative. Several authors, e.g. Reference CollinsCollins (1985) and Reference FergusonFerguson (1985), have noted this possibility and, as will be shown in a later section, there are highly glacierized basins in Greenland with negative run-off with precipitation correlations.
Run-off with Ablation
The correlation between annual run-off q t and net ablation a t is R qa given by:

which is obtained by multiplying both sides of Equation (4) by the precipitation deviation a t ′, averaging over an N year period, and applying the definitions in Equations (5) and (7).
The dependence of the run-off with ablation correlation on glacier cover is plotted in Figure 6 for the same assumptions as for Figures 4 and 5. The equation predicts a negative correlation between run-off and net ablation for basins with little glacier cover, increasing and becoming positive with increasing glacier cover. The run-off with ablation correlations given in Table II are both negative with the Thor Sø value slightly more negative than the Nordbosø value. However, the run-off with ablation correlation for Nordbosø should be positive according to Equation (9). For example, present results (S p = 0.18, S a = 0.53, R pa = −0.63, and ∝ = 0.30−0.39) give a calculated run-off with ablation correlation of +0.31 to +0.56. This theoretical correlation could be made negative according to Figure 6 by either decreasing the glacier cover or by reducing S a compared with S p.
The existence of a negative correlation between run-off and ablation is at first surprising for a basin like Nordbosø as ablation from Nordbogletscher is supposed to be a major source of run-off. For example, one of the main purposes of the glaciological work in Johan Dahl Land was to measure glacier mass balance as a step in calculating run-off. It is therefore disappointing to find that the run-off with ablation correlation is not only fairly weak but also that it is negative. The ablation measurements can be used to explain the low variability of Nordbosø run-off but the calculation of run-off itself must use precipitation as the more important variable.

Fig. 6. The correlation coefficient between annual run-off and ablation. Johan Dahl Land, calculated as a function of percentage of glacier cover. The three curves refer to values of 1, 2, and 3 for the parameter Sa/Sp.
An interesting case arises when the run-off standard deviation is a minimum, i.e. for a glacier cover α = α1, as according to Equation (10) the correlation between run-off and ablation is zero. This raises the amusing possibility that an unwary investigator might incorrectly conclude on the basis of the zero correlation that run-off was “totally unrelated to ablation”, whereas in fact ablation has the useful effect of smoothing run-off variations.
In contrast to the Johan Dahl Land situation. Equation (10) predicts a fairly strong positive correlation between run-off and ablation in highly glacierized basins and preliminary results from the PAAK 437 basin near Ilulissat/Jakobshavn in central West Greenland support this (Reference Thomsen and BraithwaiteThomsen and Braithwaite, 1987).
Other Greenland Basins
Hydrological measurements have been made in other basins in Greenland for the planning of hydropower to supply electricity to towns. The locations of these basins are shown on a map in Reference Thomsen and BraithwaiteThomsen and Braithwaite (1987). Although the present results cannot apply exactly to these basins, it would be interesting to see if the main conclusions are broadly correct.
Out of a total of 19 basins, there are 12 with at least 4 years of record up to and including 1985 (GTO, 1986[a]). Annual run-off data for these basins were used for calculating coefficients of variation of annual run-off and correlations between run-off, annual precipitation, and summer mean temperature, and the results are given in Table III together with the glacier cover α.
The precipitation and temperature data for the correlations are taken from the nearest weather station to the basin in question. The correlations between run-off and summer temperature are used as substitutes for correlations between run-off and ablation because few data for the latter are available from the basins.
The present results, with 4−9 years of record, have very sparse statistical bases compared with similar studies in other areas, e.g. Reference Tvede and TvedeTvede (1983) used run-off series with at least 35 years of record. Statistical results can therefore be unduly influenced by errors and by chance. There are also three basins (ISTA 305, KSTA 421, and PAAK 437) with uncertain amounts of glacier cover because they contain sectors of the Greenland ice sheet as in Johan Dahl Land, although the results in Table III are probably arranged in correct order of increasing glacier cover α.

Table III. Coefficient of variation c.v., correlation r qp between annual run-off and annual precipitation, and correlation r qt between annual run-off and summer temperature versus glacier cover α for 12 basins in west greenland locations of the basins given by Reference Thomsen and Braithwaitethomsen and braithwaite (1987)
For what they are worth, the results in Table III generally indicate high values of the coefficient of variation c.v. and correlation R qp between run-off and precipitation at very low values of α together with low positive, or large negative, values of the correlation R qt between run-off and temperature. For example, of the first eight basins in Table III with small amounts of glacier cover (α from 0 to 15%) there are six basins that fit this pattern reasonably well. The other two basins (KILA 419 and TSUQ 106) both have low coefficients of variation despite their lack of glacier cover and do not agree with Figure 4.
There are three basins (QAPI 113, ISTA 305, and KSTA 421) with moderate to large glacier cover which have low coefficients of variation of annual run-off, low or negative correlations between run-off and precipitation, and reasonably high correlations between run-off and temperature. These results fit the predictions of Figures 4−6. There is a fourth basin (PAAK 437) with a relatively high coefficient of variation which may be caused by the high (estimated!) glacier cover as predicted by Figure 4.
Conclusions and Outlook
There is a qualitative agreement between the results from Johan Dahl Land and the model. For example, variations in annual run-off for Nordbosø are relatively small compared with those for Thor Sø. The model also correctly predicts the existence of other basins in Greenland with negative run-off with precipitation correlations. However, the qualtitative agreement of the model with field data from Johan Dahl Land is not always good. For example, assuming the glacier cover α in the Nordbosø basin equals 0.30−0.39, gives theoretical run-off with precipitation and run-off with ablation correlations which are respectively too low and too high. It is tempting to remove these contradictions by claiming that the amount of glacier cover in the Nordbosø basin is over-estimated but it is difficult to justify an a value much less than 0.3, although the exact area of the hydrological basin cannot be determined. Another possibility is to remove the contradiction by suggesting a lower value of the ratio S a/S p than used here but the available data do not justify this.
Other possibilities are to blame the contradictions on errors in the data or shortcomings in the model. For example, inter-annual storage of precipitation in snow patches might cause glacier-free basins to mimic glacier basins, while negative correlations between precipitation and evaporation might reduce contrasts between glacier-covered and glacier-free basins.
Acknowledgements
This paper is published by permission of the Director, The Geological Survey of Greenland. The glaciological work in Johan Dahl Land was planned by O.B. Olesen and carried out by him (1978−79) and by P. Clement (1980−83). The field work was partly supported by funds from the European Economic Community and from the Danish Energy Ministry. The concept of a distinction between hydrological and glaciological basins on the Greenland ice sheet evolved in the course of many discussions between colleagues P. Clement, N. Reeh, H.H. Thomsen, A. Weidick, and the authors. G.F. Hansen prepared the drawings.











