List of symbols

Introduction

This paper reports on results from a series of experiments conducted by the author concerning snow-drift control adjacent to grade separations (bridge overpasses) on interstate highways. This work was supported by the Iowa State Department of Transportation, with the approval and recommendation of the Iowa Highway Research Board, and by the Engineering Research Institute of Iowa State University.

A number of scale-model studies have been carried out in an attempt to determine fullscale snow-drifting phenomena. Experiments that have been conducted in water include those of Reference NoremNorem (1974), Reference IsyumovIsyumov (1971), Reference CalkinsCalkins (1975), de Reference de KrasinkiKrasinski and Anson (1975), and Reference TheakstonTheakston (1970). Wind-tunnel experiments have been conducted by Reference FinneyFinney (1934, 1937, 1939), Reference NøkkentvedNøkkentved (1940), Reference BeckerBecker (1944), Reference GerdelGerdel and Strom (1961), Reference StromStrom and others (1962), and Reference BrierBrier (1972). Reference TablerTabler (1980) has conducted scale-model experiments in the atmosphere using actual snow as the modeling material. Some of these experiments have attempted to satisfy similitude requirements, at least partially. In others, modeling laws have been ignored. The current experiments demonstrate the utility of a new application of similitude fundamentals which makes use of theoretical relationships for mass-transport rate and aerodynamic roughness of saltating particulate material.

Similitude laws

If simple dimensional analysis is used to group the important variables involved in drifting phenomena, the following list of dimensionless parameters can be written:

It is impossible, of course, in a small-scale model to satisfy all of these parameters simultaneously. Reference GerdelGerdel and Strom (1961) considered the parameters 1 to 4 of the foregoing list as those of primary importance. Reference OdarOdar (1965) and Reference KindKind (1976) have also studied the problem in some detail. The parameters considered important by these and other investigators are listed in Table I. These dimensionless quantities have been discussed previously by the author (Reference IversenIversen, 1979, unpublished; Reference IversenIversen and others, 1973, 1975, 1976; Reference RingRing and others, 1979).

Table I. Modeling parameters considered by various investigators

Obviously, there is some disagreement as to which similitude parameters are significant. The most popular parameter is the Froude number, parameter number 3, chosen by all seven investigators as appropriate for similitude. That the Froude number by itself is not an appropriate parameter is shown by the results of the current investigation.

As shown previously (Reference IversenIversen and others, 1976; Reference IversenIversen, 1979), combinations of some of the similitude parameters can be obtained by using theoretical relationships. The particle trajectory equations of motion are used to group parameters 1, 3, 8, and 15 to obtain

17.

18.

The equivalent roughness height in saltation z ₀’ is assumed to be proportional to ρu _⋆²/ρpg (instead of u _⋆²/g as assumed by Reference OwenOwen (1964)) in order to account for the effects of particle-to- fluid density ratio (Reference WhiteWhite and others, 1976). Thus (Reference IversenIversen and others, 1976; Reference IversenIversen, 1979)

19.

A modification of Reference BagnoldBagnold’s (1941) mass transport rate,

is used to obtain a transport-rate similitude parameter (Iversen, unpublished)

20.

Here A is the planform drift area. The differential d(A/L ²) can be replaced by d(A _c/LH) (cross-section area) or by d(V/L ²H) (drift volume).

Odar (1962, 1965) and Reference KindKind (1976) have used theoretical aids in order to group modeling parameters or to determine important variables. Odar also considered the dimensionless particle equations of motion. In one case (Reference OdarOdar, 1965) he defines the dimensionless time as t(g/L) ^½ rather than tU/L and instead of parameters 17 and 18 bis resulting parameters are C_Dρu_⋆²/ρpgD_p and gL/u _⋆². In the other case (Reference OdarOdar, 1962) he lists the two parameters ρpgL/pu _⋆² and gL/u _⋆² as the important ones resulting from the particle equations of motion. Reference KindKind (1976) also considers the equivalent roughness height z_o' to be important in modeling, and following Reference OwenOwen's (1964) results for z₀'≈ u_⋆²/g, believes that the resulting Froude number,

is the most important modeling parameter. It is the author's experience, gained using particles of various densities, that the equivalent roughness height z₀' is affected by density ratio ρp/ρ and that parameter 19 is thus more appropriate.

For modeling the gross features of full-scale snow-drifts, the mass transport rate parameter number 20 appears to be the most important. The value of the transport rate is significantly affected, however, as shown below, by changes in the value of roughness parameter 19. Parameters 17 and 18, derived from the particle equations of motion, appear to be important only in determining the characteristics of small-scale surface features (ripples) and thus can be ignored unless the small-scale features begin significantly to affect gross drift formation geometry.

In the study of grade-separation snow-drift problems two models were tested, one with a vertical geometric distortion in order to assist in ascertaining the effect of parameter 19. Thus, allowing for the possibility of vertical geometric distortion and using Jensen's criterion (Reference JensenJensen, 1958; Reference CermakCermak, 1975) for normal roughness modeling, the similitude problem becomes, for example (parameters 5, 6, 8, 13, 19, 20),

(1)

The Reynolds-number requirement, for relatively unstreamlined or rough-surface models, is usually specified as a minimum requirement; i.e. the model Reynolds number must exceed a minimum value, above which changes with Reynolds number are small (Reference CermakCermak, 1975; Reference IversenIversen, 1976).

Topographic and particle models

Two models of the highway grade-separation structure were constructed. Model 1 was built at a 1 : 120 scale and Model 2 was built at the same scale horizontally but with a 1 : 60 scale in the vertical direction. Both models were covered with cloth to simulate grass except for the highway lanes which were smooth plastic (Reference RingRing and others, 1979). Three particles were selected for simulation of snow (Iversen, unpublished): 269 pm walnut shell (1 100 kg/m³), 101 µm glass spheres (2 500kg/m³), and 49 μm dense glass spheres (3990 kg/m³).

The models were placed at various orientations to the wind in a boundary-layer wind tunnel (1.2 - 1.2 - 7 m³ test section). The boundary layer depth at the model location (5 m down-wind) was increased to 0.25 m by turbulence-generating spires placed at the test section entrance. Particle material was placed to a uniform depth of 0.015 m (0.03 m for Model 2)across the test section width from 2.3 to 3.7 m down-wind of the test section entrance prior to the start of each experiment. Plan-view photographs of the model were taken at recorded times during each test run in order to measure the planform drift area on each stretch of highway lane as a function of time.

Bare-model calibration

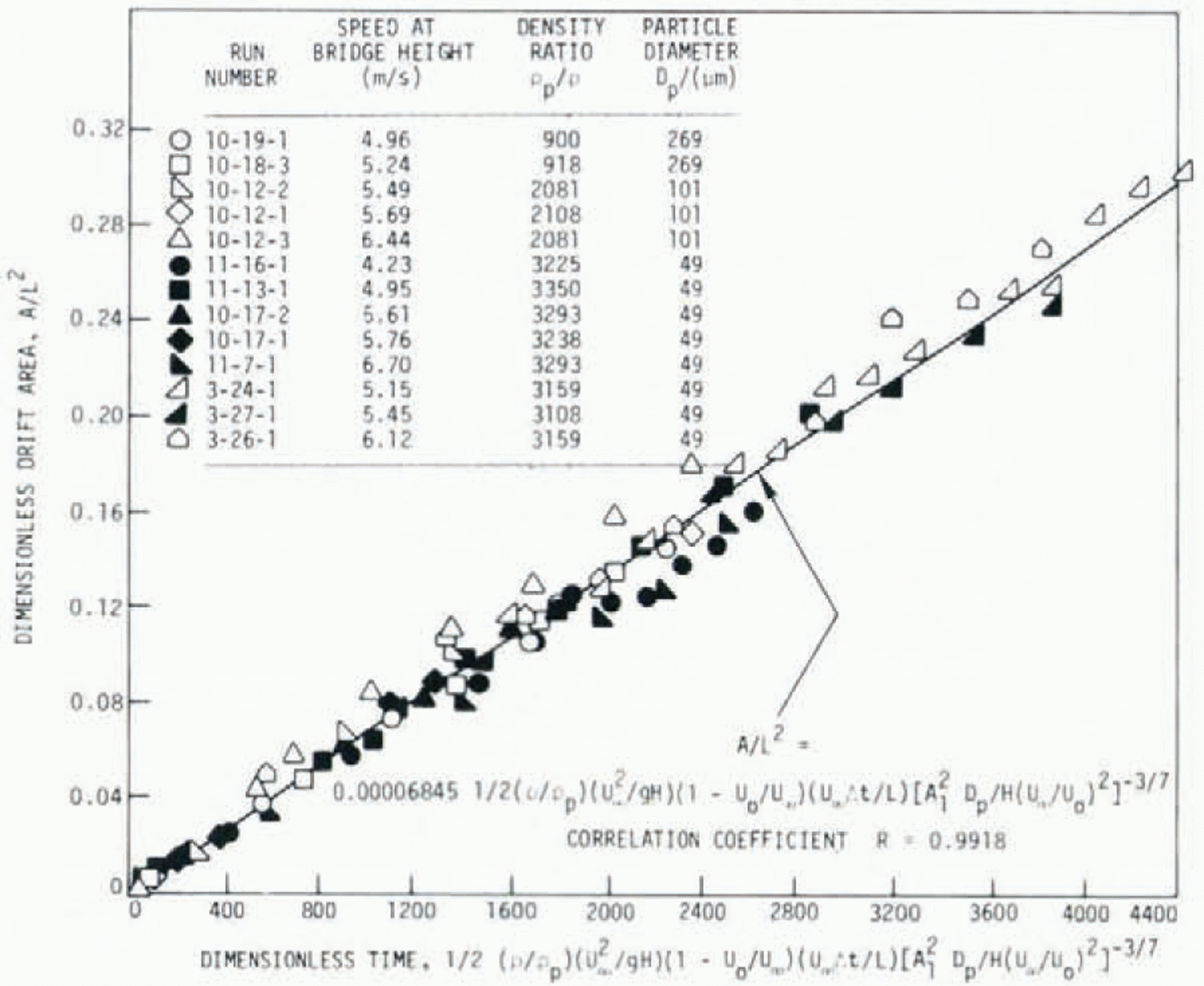
Both the undistorted and vertically-distorted grade-separation models were tested without simulated drift-control vegetation not only in order to obtain comparison with control planting configurations but also to obtain appropriate similitude relationships for more exact configuration comparisons and for possible extrapolation to full scale. With the wind direction parallel to the bridge center line, a total of 13 bare (simulated grass only) model experiments Figure 1 were analyzed to produce the relationship desired. Ten of these experiments were with the undistorted model (Model 1) and three with the distorted model (Model 2). Photographs of some of these experiments are shown in Figure 1. Two experiments were with the 268 μm shell particles, three were with the 101 µm light glass, and the other eight were with the 49 µm dense glass. The 49 µm dense glass was used for all the remaining drift-control experiments. The planform drift area A divided by L ² (bridge length squared) is shown for the 13 experiments as a function of dimensionless time in Figure 2.

Fig. 1. Photographs of bare (grass only) model calibration experiments. Scale-model cars were added after experiment was completed,

a. Run No. 2-24-1, wind direction left to right at 40° to bridge center line. Model 1.

b. Run No. 12-7-1, wind direction left to right at 20° to bridge center line. model 1.

c. Run No. 3-27-1, wind direction left to right at 0° to bridge center tine. Model 2.

Fig. 2. Plan-view drift area on interstate highway lanes as a function of time from the start of drifting. Speed ranges from 4.23 m/s to 6.70 m/s at 0° wind direction. Particle density ranges from 1 100 to 3 990 kg/m ³ and particle diameter from 49 to 269 µm.

Table II. Values of modeling parameters from calibration tests

The range of values of the four modeling parameters in the 13 bare model tests together with the corresponding full-scale values are depicted in Table II. The values of area A correspond to the snow-drift area (in plan) covering a 42 inch (105 cm) length of both lanes of highway including the shoulders. Obviously, the first two parameters are not modeled. These two parameters are of primary importance only if small-scale surface forms, such as ripples, are to be modeled to scale. Because of the use of the distorted model, the values of the third and fourth parameters, namely the roughness and mass-rate parameters, overlap the corresponding full-scale values giving more confidence in the results of the scale-model tests, since the third and fourth parameters are by far the most important in determining the gross drifting features and drift accumulation-rate.

The dimensionless rates of change of drift area for the bare model experiments were calculated using parameter 20. The results are shown in Figure 3 with the values of the mass transport rate parameter 20 plotted versus the saltation roughness parameter 19. The trend of decrease in the mass-rate parameter with increase in roughness is clear. In the absence of some theoretical relationship, a simple power-law equation was fitted to these data with the result as shown on the Figure. The full-scale values of roughness parameter are just to the left of Figure 3 most of the model values. It could thus be expected that the full-scale dimensionless drift rate (parameter 20) would be relatively somewhat larger than the model values. The dimensionless planform drift area is plotted against the combined mass-rate-roughness parameter in Figure 4. The correlation is quite good with the correlation coefficient r = 0.991 8 (r = ± 1 is a perfect correlation; r = slope multiplied by the ratio of horizontal and vertical standard deviations).

Fig. 3. Dimensionless drift rate using mass-rate parameter 20 versus roughness parameter 19. Same experiments as in Fig. 2.

Fig. 4. Dimensionlus drift area versus combined mass-rate-roughness parameter. Same experiments as Figs 2 and 3.

In order to evaluate the propriety of the various similitude parameters that other investigators have used or could possibly have used in comparison with the current mass-rate— roughness function, an attempt was made to correlate the dimensionless rate of change of area d(A/L ²) /d(U _∞Δt/L) as a function of several parameter possibilities. The results are found in detail in Reference RingRing and others (1979). The following equations with the corresponding correlation coefficients summarize the results:

(2)

(3)

(4)

(5)

The correlation using the Froude number U _∞²/gH is not valid with a correlation coefficient of only 0.706 for Equation (2). Equation (3), which is equivalent to using Bagnold’s expression for the mass-rate equation and which takes the density ratio ρ/ρ _p into account, results in a considerable improvement and a relatively good correlation. Reference CalkinsCalkins (1975) indicated that ρU ²/ρ _pgL was an appropriate similitude parameter although he did not explain why he thought so. Calkins went on to abandon (his parameter (which he labeled the densimetric Froude number) because full-scale projected speeds arc unrealistic when using water as a model fluid. Use of the modified mass-transport rate (used to derive parameter 20) improves the correlation as in Equation (4), and addition of the roughness parameter (parameter 19) as in Equation (5) results in the best correlation coefficient. Reference KindKind’s (1976) and Reference KawamuraKawamura’s (1951) expressions for mass-transport rate resulted in values of r of 0.93 and 0.96, respectively, which are not as good as those for Equation (4), but still represent reasonably acceptable values of correlation coefficient.

Fig. 5. Dimensionless drift area versus combined mass-rate—roughness parameter. Wind direction 20° to bridge center line. Comparison of uncontrolled (bare model) and two different plan snow-drift control configurations. Model 1.

Testing the simulated vegetative snow-drift control

Simulated rows of bushes (3 m full-scale height) were placed on the grade-separation model to act as snow-drift control barriers. Fifty-one experiments were performed with a variety of control configurations and with wind-speed direction angles of 0°, 20°, and 40° to the bridge center line. Typical results are shown in Figure 5 and 6, Two control configurations, one of good and one of mediocre performance, are compared in Figure 5 with a baremodel calibration at a 20° wind direction angle. It is as easy to create a planting configuration that can be considerably worse than no control as to create one that is a considerable improvement, such as plan L-20. Photographs of another experiment at 40° wind direction are illustrated in Figure 6. Results of all simulated vegetation experiments are reported in Reference RingRing and others (1979).

Fig. 6. Photographs of Model 1 experiment (run 2-23-1) with wind direction from left to right at 40° to bridge center line. Scale-model cars were added after experiment was completed.

a. Side view (approximately 45° from horizontal).

b. Plan view.

Effect of vertical distortion

The results with the vertically distorted model (Model 2) at 0° wind direction for one bare-model experiment and one controlled-model experiment are shown in Figure 7 together with the corresponding results for the undistorted Model 1. The results for both configurations are displaced to the left for Model 2 compared with Model 1. The reason for this is that Model 2 is horizontally distorted as well as vertically distorted in conditions where there are separated flow or reduced-speed regions such as the lee side of the fill slope under the bridge and down-wind of the simulated plant control. The regions of reduced speed extend farther down-wind than in the undistorted Model 1 (or in full scale) because of the greater relative height of the fill slope and plant control in the distorted Model 2. Thus, early drifting occurs farther down-wind for Model 2 than for Model 1 and the drift area on the roadway is larger for corresponding times as shown in Figure 7. That Model 2 still gives valid relative results, at least for certain configurations, is shown by the fact that the two sets of curves are parallel and displaced vertically about the same distance. The curves would not be parallel without use of the combined parameter which includes the effect of roughness.

Fig. 7. Dimensionless drift area verms combined mass-rate-roughness parameter. Comparison of 0° wind-direction tests, controlled and uncontrolled, using Model 1 (true geometric model) and Model 2 (vertical geometric distortion factor of two).

Extrapolation of model results to full scale

Previous investigators have usually used the Froude number U ²/gL as a means of determining the full-scale wind-speed and the duration of the modeled snow-storm time. This is believed to be incorrect as judged using the preceding similitude analysis and wind-tunnel test results. If, however, the Froude number is used (albeit incorrectly) as a means of extrapolation, then the full-scale-model wind-speed ratio U/U _m would just be the square root of the length ratio L/L _mThe time ratio Δt/Δt_m would be the same value as the speed ratio. Using run number 10-17-1 as an example (model speed =5.76 m/s and time duration = 18 minutes), the Full-scale wind-speed would he 63.05 m/s (141 miles/h) and the duration would be 3 h 17 min, which are not very realistic values.

According to the wind-tunnel results of the 13 bare-model experiments, the appropriate extrapolation is to equate the combined mass-transport rate roughness parameters for model and full scale:

(6)

It is assumed that everything is known in this equation except the full-scale values of U and Δt (or the model values of U and Δt which represent a given full-scale storm). Thus, another equation is needed in order to solve for the two unknowns of the second equation. One equation can be obtained by assuming that the ratio of particle speed to wind speed is the same in model and full scale. The second equation would then be

(7)

For the example run 10-17-1, the values of full-scale wind-speed U and lime duration Δt would be 14.68 m/s (32.8 miles/h) and 14 h 6 min, respectively.

The ratio of particle to wind-speed is not likely to be the same in full scale as in the model so it is probably more appropriate to search for another second equation. This can be done by equating the modified “densimetric Froude number”, i.e.

(8)

Then, in order to satisfy Equation (6),

(9)

Equations (8) and (9) result in full-scale values for run 10-17-1 of 22.16 m/s (49.6 miles/h) for wind-speed and 5 h 32 min for storm duration. If the fundamental similitude Equation (6) is valid for all wind-speeds, then either of the wind-speed and time set of values of 14.68 m/s and 14 h 6 min or 22.16 m/s and 5 h 32 min are appropriate since both sets satisfy Equation (6). There probably are at least subtle differences with changes in wind-speed, however, and thus the latter set is probably more valid (based on the investigator’s experience and intuition).

Conclusions

The dimensionless parameters derived by simple dimensional analysis for a given similitude problem can often be combined theoretically for modeling purposes. If not all original dimensionless parameters can be satisfied at model scale, then the model is distorted and some means of interpreting the effect of distortion must be determined. In the case of snow-drift modeling, it appears that the equivalent aerodynamic roughness height with material in motion derived by theoretical considerations of equivalent roughness is a significant distorted similitude parameter. The effect of varying the amount of roughness height distortion was determined by using particles of different diameter and density, different wind-tunnel speeds, and by testing a model with vertical geometric distortion as well as with a true geometric model.

The primary modeling parameter is considered to be the mass-rate parameter (parameter 20) which is derived from consideration of the amount of mass/unit time which can be transported by the wind. This parameter is combined empirically with the roughness parameter to correlate model-scale snow-drift accumulation data successfully as well as to predict equivalent full-scale wind-speeds and storm durations. The combined parameter has been used to compare a variety of drift-control techniques adjacent to an interstate highway gradeseparation crossing.