Basal topography

The three outlet glaciers were surveyed with a radio-echo sounder and differential GPS (DGPS) equipment in the period 2000–05 (Reference Magnússon, Pálsson, Björnsson and GuðmundssonMagnússon and others (2012) provide details of the method). Point measurements were carried out in the ablation area, whereas continuous profiles were surveyed in the accumulation area (Fig. 2a). The vertical accuracy of the basal topography is 5–20 m, depending on the location. A small depression below the terminus of Skálafellsjökull reaches 100 m below sea level. Heinabergsjökull has excavated a 10 km long trench, which underlies the majority of its ablation area, reaching maximum depths of 220 m below sea level. The bed of Fláajökull is 200 m below sea level in the ablation area (Fig. 2a). Previous model simulations on neighbouring Hoffellsjökull show that using a filled trench or the current basal topography, had negligible effect on the evolution simulations (Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). We thus use the measured bed DEM (unfilled trench) in all model runs.

Fig. 2. (a) Basal topography derived from radio-echo sounding measurements (shown with white lines and dots) of Skálafellsjökull, Heinabergsjökull and Fláajökull. The glacier margin in 2000 is shown. Proglacial lakes are shown in light blue, and nunataks in white. (b) Surface topography from the 2010 lidar DEM shown with 100 m contours and glacier outlines at different times from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others (2014a). The location of the MODIS-derived snowline in the period 2007–11 is shown in light blue.

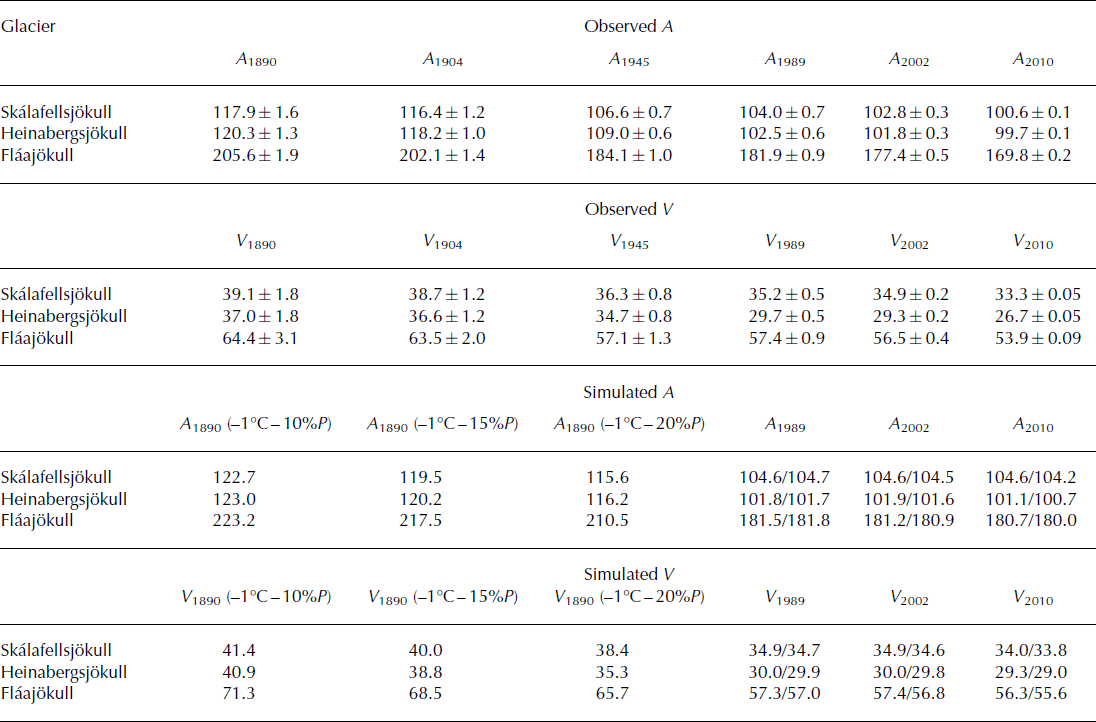
Glacier area and volume changes 1890–2010

The evolution of the area and volume of the three outlet glaciers during the period 1890–2010 (Fig. 2b; Table 2) has been derived from a new glacier inventory. DEMs of the ∼1890 glacier surface were created from glacial geomorphological features and historical data from the time of the LIA maximum (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014b), whereas DEMs from 1904, 1945, 1989, 2002 and 2010 were generated from maps, aerial images, DGPS surveys and a lidar survey (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a). The most accurate DEMs were produced with airborne lidar technology in late August–September of 2010 and 2011 (IMO and IES, 2013). The glaciers started to retreat from their terminal LIA moraines after 1890 and retreated during most of the 20th century. They halted or advanced slightly in the 1960s–80s due to lower temperatures, but the retreat accelerated after ∼2000. During the first decade of the 21st century, the glaciers experienced the highest rate of mass loss in the post-LIA period (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a).

Table 2. Observed area (A; km²) and volume (V; km³) (from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a) and simulated (using temperature from Hólar and LT-DP) area and volume in 1989, 2002 and 2010, both from uncoupled and coupled runs (see Fig. 11)

Mass-balance observations

Mass-balance measurements have been carried out on Vatnajökull since 1991, and the majority of the stakes are located on the northern and western part of the ice cap (Reference Björnsson and PálssonBjörnsson and Pálsson, 2008). Six stakes were on a profile from the terminus up to the ice divide on Breiðamerkurjökull, three stakes were measured on Hoffellsjökull, and a few survey sites were located in the accumulation area of the studied glaciers (Fig. 1; Reference Björnsson and PálssonBjörnsson and Pálsson, 2008). The variation of mass balance with elevation on southeast Vatnajökull is shown in Figure 3a. Ablation of up to 9mw.e.a⁻¹ is observed during summers on Breiðamerkurjökull and Hoffellsjökull, and negative winter balances at the termini (Reference Björnsson and PálssonBjörnsson and Pálsson, 2008). Two new stakes were added to the mass-balance survey network in 2009 in the accumulation area of Skálafellsjökull and Fláajökull. Digital mass-balance maps, for every year since 1996, have been manually interpolated (Reference Björnsson, Pálsson and HaraldssonBjörnsson and others (2002) provide details of the method), using the in situ mass-balance measurements and the observed mass-balance gradient on southeast Vatnajökull (Fig. 3a). The resulting maps are integrated over the whole glacier area to calculate the mean specific mass balance shown in Figure 3b for the three outlets in this study.

Fig. 3. (a) The annual mass balance (b _n) measured at stakes on Breiðamerkurjökull (circles), Skálafellsjökull and Fláajökull (crosses) and Hoffellsjökull (triangles) in the period 1996–2012. (b) Mean specific winter (b _w, blue), summer (b _s, red) and net balance (b _n, black) for Skálafellsjökull (triangles), Heinabergsjökull (circles) and Fláajökull (crosses) for the period 1996–2013. New mass-balance stakes were added to the network in 2009 (the timing is shown with a vertical line).

Temperature and precipitation data from meteorological stations

Temperature and precipitation records are available from two lowland meteorological stations south of Vatnajökull (Fig. 1; Table 3), at Fagurhólsmýri (16 m a.s.l.; 8 km south of Öræfajökull) and Hólar in Hornafjörður (16 m a.s.l.; 15 km south of Hoffellsjökull). The temperature record at Hólar is available for the period 1884–90 and since 1921 (Fig. 4), while precipitation measurements started in 1931. The temperature record at Fagurhólsmýri goes back to 1898, and precipitation has been measured from 1921 until 2008 (Fig. 4). Temperature records from other stations around Iceland were used to extend the local records back to 1860 and fill in gaps by an iterative expectation maximization algorithm (described in Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). To extend the precipitation record of Fagurhólsmýri back to 1860, Reference AðalgeirsdóttirAðalgeirsdóttir and others (2011) applied a linear regression between the monthly values of temperature (Hólar) and precipitation (Fagurhólsmýri) and tuned it with the available precipitation records.

Table 3. Mean summer (June–August) temperature (T) at Hólar in Hornafjörður and annual precipitation (P) at Fagurhólsmýri averaged over the respective time periods. The temperature and precipitation during the period 1860–90 are estimated by Reference AðalgeirsdóttirAðalgeirsdóttir and others (2011)

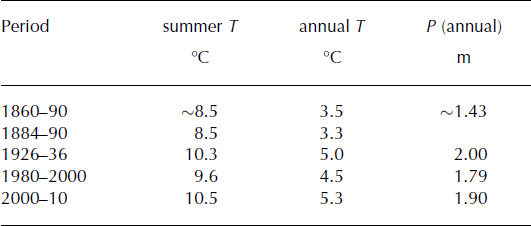
Fig. 4. (a) Mean summer (June–August) and annual temperature (grey lines) at Hólar in Hornafjörður and a 5 year running average (black lines). (b) Annual precipitation at Fagurhólsmýri. Grey boxes indicate the time period of reconstructed temperature and precipitation (for details of the reconstruction see Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). The average values of the baseline period 1980–2000 used for reference in the computations are shown with orange lines.

The mass-balance model

Our mass-balance model is a PDD (temperature index) model that has been developed for temperate glaciers in Iceland and the Nordic countries (Reference Jóhannesson, Sigurdsson, Laumann and KennettJóhannesson and others, 1995; Reference JóhannessonJóhannesson 1997) and has previously been used in several glaciological studies in Iceland (Reference Aðalgeirsdóttir, Jóhannesson, Björnsson, Pálsson and SigurðssonAðalgeirsdóttir and others, 2006, Reference Aðalgeirsdóttir2011; Reference JóhannessonJóhannesson and others, 2007; Reference Guðmundsson, Björnsson, Jóhannesson, Aðalgeirsdóttir, Pálsson and SigurðssonGuðmundsson and others, 2009a). Glacier accumulation and ablation are computed from (1) daily precipitation and temperature values from meteorological stations outside the glacier or (2) distributed fields of daily precipitation from the LT model and temperature values from meteorological stations outside the glacier. Melting of snow and ice is computed from the number of PDDs, using different degree-day factors (amount of melting per PDD) for snow and ice and a constant snow/rain threshold (1°C) (Reference JóhannessonJóhannesson, 1997). Refreezing of meltwater and wetting of the snow by melt- or rainwater are computed as a specified fraction of the remaining snow. This is a small mass-balance component for the temperate Icelandic glaciers where the winter cold wave in the snowpack is eliminated by percolating meltwater every summer even at the highest altitudes (e.g. Reference Björnsson and PálssonBjörnsson and Pálsson, 2008). Refreezing at depth in older firn therefore does not occur. The main effect of refreezing and retention for Icelandic glaciers is a delay in runoff from the glacier in the early part of the melt season that has only a small effect on the annual mass balance calculated here (Reference Jóhannesson, Sigurdsson, Laumann and KennettJóhannesson and others (1995) provide more details).

The in situ mass-balance data from southeast Vatnajökull were used to calibrate the mass-balance model using the LT-DP. The precipitation model extends to 2010, and mass-balance measurements started in 1996, resulting in a 14 year calibration period. The mass-balance model calculates daily mass-balance values, but the model output is defined for summer (1 May–30 September) and winter (1 October–30 April) for every balance year. The degree-day scaling factors for snow (ddf_s) and ice (ddf_i), are determined by minimizing the root mean square (RMS) between measured and modelled mass balance (e.g. Reference Jóhannesson, Sigurdsson, Laumann and KennettJóhannesson and others, 1995). The ddf_s is derived from seven points in the accumulation area, and the ddf_i from six points in the ablation area (Fig. 1). The best fit (lowest RMS value) was found when using ddf_s =3.7 mm w.e. °C⁻¹ d⁻¹ and ddf_i = 5.5 mm w.e. °C⁻¹ d⁻¹ (Table 4). These values are in the range of previously determined degree-day factors from studies on Langjökull and Vatnajökull (Reference Guðmundsson, Björnsson, Pálsson and HaraldssonGuðmundsson and others, 2003; Reference Flowers, Björnsson, Geirsdóttir, Miller and ClarkeFlowers and others, 2007; Reference JóhannessonJóhannesson and others, 2007; Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). The modelled and measured winter and summer mass balance are plotted in Figure 5. The mass-balance model explains 87% of the variance of the winter balance and 92% of the variance of the summer balance in the period 1996–2010. However, the correlation is worse when considered separately for the accumulation and ablation areas.

Table 4. Degree-day factors for snow and ice used in mass-balance modelling studies on Vatnajökull, determined by minimizing RMS between observed and modelled mass balance

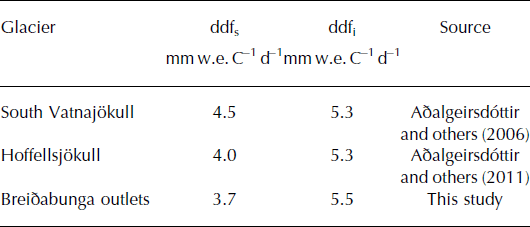
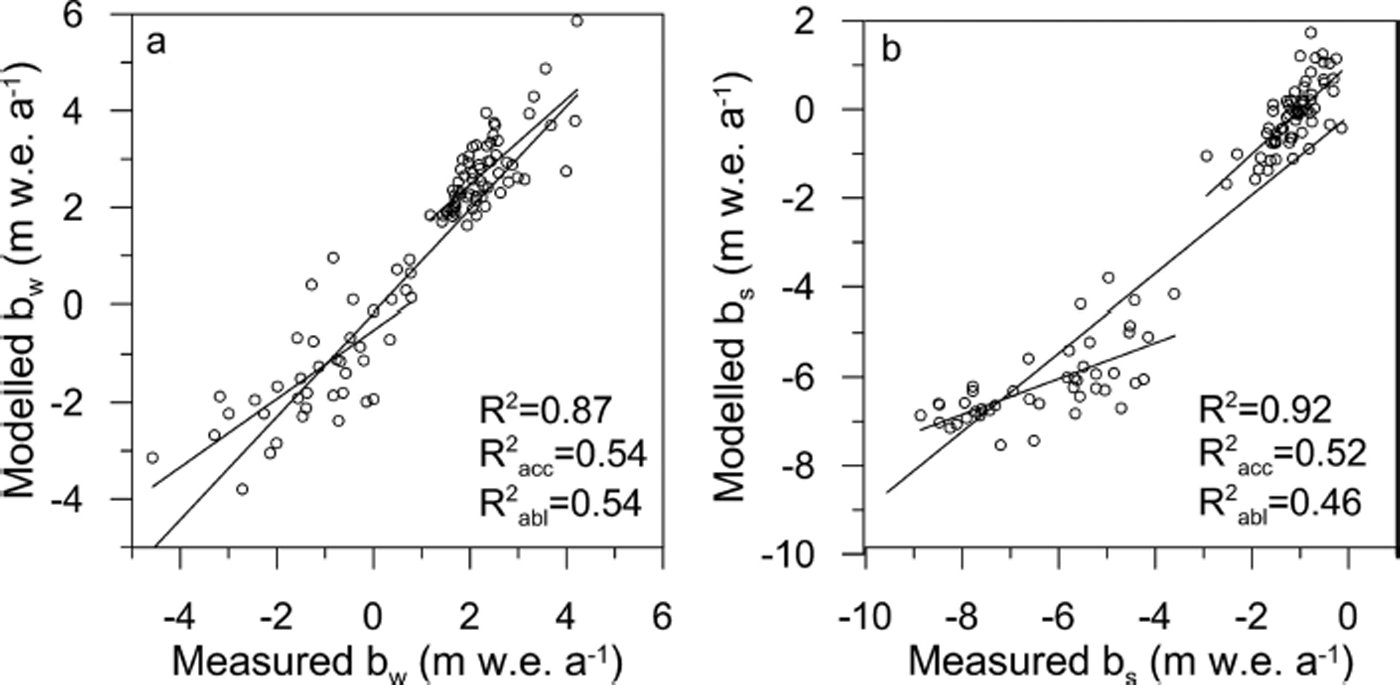
Fig. 5. Measured vs modelled (using LT-DP and ddf_i = 5.5 mm w.e. C⁻¹ d⁻¹ and ddf_s = 3.7 mm w.e. °C⁻¹ d⁻¹) winter (a) and summer (b) balance of southeast Vatnajökull in the period 1996–2010. The linear relationship is shown and the R ² value indicates the linear regression coefficient.

The ice-flow model

Our ice-flow model is based on the SIA and vertically integrated continuity equation, neglecting longitudinal stress gradients, bed isostatic adjustments and seasonal variations in sliding (e.g. Reference AðalgeirsdóttirAðalgeirsdóttir, 2003; Reference Aðalgeirsdóttir, Jóhannesson, Björnsson, Pálsson and SigurðssonAðalgeirsdóttir and others, 2006). Glen’s flow law with an exponent n = 3 is assumed as a constitutive equation for ice (e.g. Reference Cuffey and PatersonCuffey and Paterson, 2010). In terms of numerical implementation, this version of the model uses the finite-element method with triangular elements, and has previously been applied to simulate the evolution of Hoffellsjökull (Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). The average slope of the studied outlet glaciers is in the range 3–4°, and the aspect ratio (typical thickness to characteristic length for the ice body) is on the order of 10⁻³, which is acceptable for application of the SIA method (e.g. Reference Le Meur, Gagliardini, Zwinger and RuokolainenLe Meur and others, 2004).

Several values for the rate factor (A) in Glen’s flow law are applied to select one that best simulates the observed glacier geometry. In previous studies (Reference Aðalgeirsdóttir, Jóhannesson, Björnsson, Pálsson and SigurðssonAðalgeirsdóttir and others, 2006; Reference Guðmundsson, Björnsson, Jóhannesson, Aðalgeirsdóttir, Pálsson and SigurðssonGuðmundsson and others, 2009a) the applied rate factor was 6.8 × 10⁻¹⁵ s⁻¹ kPa⁻³, and in the more recent study of Reference AðalgeirsdóttirAðalgeirsdóttir and others (2011) the rate factor A = 4.6 × 10⁻¹⁵ s⁻¹ kPa⁻³ was determined from a series of model runs for Hoffellsjökull to best fit the observed velocity field. Based on the results of several ice-flow model studies, the recommended value for the rate factor for temperate ice is A = 2.4 × 10⁻¹⁵ s⁻¹ kPa⁻³ (Reference Cuffey and PatersonCuffey and Paterson, 2010). Model runs including explicit basal sliding were made, applying a Weertman-type sliding law (Reference PatersonPaterson, 1994), where the sliding velocity (V _s) is assumed proportional to the basal shear stress, τ _b, to a power of m (V _s = Cτ _b ^m ). C is the sliding parameter, and the exponent m is assumed equal to 3 in our model runs. No data are available to determine the relative contributions of deformation and sliding velocities to the glacier flow. The chosen horizontal resolution of the input files and the triangular elements of the model mesh was 200 m. The ice divides are kept at a fixed location in the model and no flow is allowed across them. Thus no ice-divide migration due to mass-balance changes is permitted. The ice-flow model is run both coupled and uncoupled with the mass-balance model using LT-DP in the time-dependent simulations. When coupled, the changing glacier surface elevation is updated each year. This affects the calculated mass balance, whereas in uncoupled runs the mass balance is computed on the same topography throughout.

Constant precipitation gradients and new stake data

Simulations with the mass-balance/ice-flow model were carried out using constant vertical and horizontal precipitation gradients: 0.5 per 100 m in the vertical, 0.0005 and −0.0008 per 100 m in the horizontal east and north directions, respectively. Temperature at Hólar in Hornafjörður and precipitation at Fagurhólsmýri were used to force the model, with the same degree-day factors for snow and ice as in previous studies on south Vatnajökull (Reference Aðalgeirsdóttir, Jóhannesson, Björnsson, Pálsson and SigurðssonAðalgeirsdóttir and others, 2006). These simulations revealed a surface lowering of >90 m in the accumulation area, and a volume reduction of 20–30% between the start and end of the simulation (Fig. 6a; Table 5). The results indicate that the mass balance is underestimated in the accumulation area of the glaciers by the constant precipitation gradients.

Table 5. Difference (%) between volume and area at the start and end of 300 year simulations using the mass-balance model with constant precipitation gradient (CPG), the winter mass balance (b _w) revised with downscaled precipitation data from the WRF model and the mass-balance model using LT-DP, with rate factors between A = 4.6 × 10⁻¹⁵ s⁻¹ kPa⁻³ and A = 2.4 × 10⁻¹⁵ s⁻¹ kPa⁻³, and including basal sliding (C = 10 × 10⁻¹⁵ m a⁻¹ Pa⁻³). Constant temperature and precipitation forcing is applied using the average of the baseline period 1980–2000, and starting with the smoothed 2000 glacier surface DEM (Figs 6 and 8)

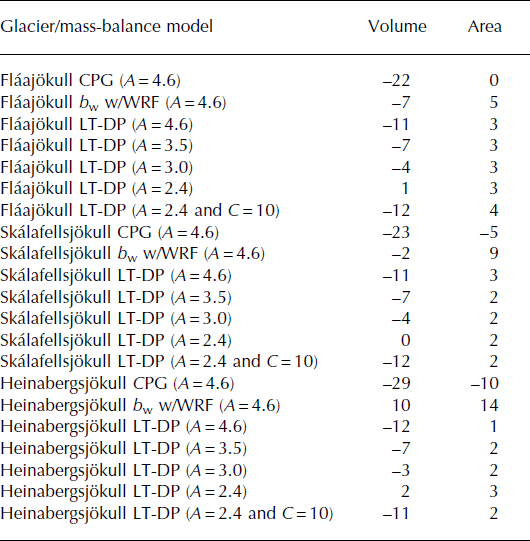
Fig. 6. The elevation difference between the initial measured surface from 2000 and the final simulated glacier surface of a 300 year model run using constant temperature and precipitation forcing of the baseline period 1980–2000. (a) The mass-balance model using a constant precipitation gradient (CPG). (b) Interpolated mean winter mass-balance grid for the period 1996–2006 revised with the downscaled winter precipitation from the WRF model. (c, d) Mass-balance model using downscaled precipitation from the LT model (LT-DP). In the simulations in (a–c) a rate factor of A = 4.6 × 10–15 s⁻¹ kPa⁻³ is used. In the flow model and the simulation shown in (d) a rate factor of A = 2.4 × 10–15 s⁻¹ kPa⁻³ is applied.

Experience from fieldwork led to the suspicion that winter accumulation on the southern slopes of Breiðabunga is higher than on the ice divide (as measured at BB0 and B19; Fig. 7a). Two new stakes (Sk01 and Fl01; Fig. 7b) were therefore added to the mass-balance network in the fall of 2009, which confirmed that snow accumulation is greater south of the plateau (Fig. 7b). It is clear that the stakes on the ice divides do not adequately represent the winter mass-balance variation of the studied outlets (Fig. 7a).

Fig. 7. (a, b) Manually interpolated average winter balance (b _w) maps for (a) 1996–2009, based on in situ measurements, and (b) 2010–13, when stakes Skf01 and Fl01 have been added to the mass-balance network. (c) Average winter precipitation (av.wP) map for 1996–2006 simulated with the WRF model. (d) Average winter precipitation map for 1996–2004 simulated with the LT model.

Winter mass-balance maps from in situ measurements revised with downscaled precipitation data from the WRF model

In order to explore the possible deficit of the winter mass balance in the accumulation area of the three glaciers, as found when using the constant precipitation gradients in the mass-balance model, two independent modelled precipitation datasets were analysed: the downscaled winter precipitation fields derived from the WRF model and from the LT model (Fig. 7c and d). Both datasets indicate that the winter precipitation distribution is more complex in this area than can be accounted for by constant precipitation gradients. The greatest snow accumulation is to the south of the Breiðabunga plateau according to both model results (Fig. 7c and d).

The manually interpolated winter mass-balance maps of the period 1996–2006 were revised with the downscaled precipitation data from the WRF model. Summer melt was deduced from the degree-day model, using the average temperature from Hólar in Hornafjörður in the period 1980–2000. Forcing the ice-flow model with the interpolated mass-balance maps improves the simulated glacier geometry. Less surface lowering occurs in the accumulation area, and the glaciers reach equilibrium without losing the same ice volume as when forcing it with the constant precipitation gradients (Fig. 6a and b; Table 5). The outlets advance beyond the 2000 margin (Fig. 6b), resulting in a 5–14% increase in area compared to the area in 2000 (Table 5).

LT-DP and tuning of the ice-flow rate factor

Figure 6c shows the elevation difference between the start and end of the simulation. The surface lowering in the accumulation area is similar to when using the revised mass-balance maps with the WRF data, but less thickening in the ablation area (cf. Fig. 6b and c). The volume loss is on the order of 2–12%, and the simulated areal extent is slightly larger than the observed area (Fig. 6c; Table 5). The glaciers undergo less surface lowering in the accumulation area than in earlier simulations (Fig. 6a–c), and the modelled volume and area are closer to the observations, the difference being within 3% (Table 5). In view of the good agreement between observed and simulated glacier geometry, a series of simulations with various rate factors and adding explicit sliding were carried out (Table 5). The best fit (both volume and surface profiles) is obtained with a rate factor of A=2.4 × 10⁻¹⁵ s⁻¹ kPa⁻³, representing stiffer ice (Fig. 6d). Adding sliding (C = 10 × 10⁻¹⁵ m a⁻¹ Pa⁻³) gives the same results as having softer ice (A = 4.6 × 10⁻¹⁵ s⁻¹ kPa⁻³) (Table 5).

Summary of simulations using various precipitation data for the mass-balance model

A further comparison of the simulations described above is presented in Figure 8, where longitudinal surface profiles from the ice divide to the terminus are shown, and compared with a number of observed surface profiles. The substantial lowering of the glacier surface using constant precipitation gradients in the mass-balance model is evident on the modelled surface profiles on all three outlets. The simulations using the revised winter mass-balance map with precipitation from the WRF model indicate an overestimation of the winter mass balance, as all three outlets advance ∼1 km beyond the observed margin, and thickening in the ablation zone of up to 100 m (Fig. 6b). Simulations using the LT-DP show the best fit with the observed surface profiles (Fig. 8).

Fig. 8. Longitudinal profiles (locations shown in Fig. 2b) showing the glacier thickness and extent at different times according to observations (filled-in mauves, blues and green areas) from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others (2014a) and the various simulations (lines) using constant temperature and precipitation forcing (average of the baseline period 1980–2000), except for the dark-blue surface profile (−1°C and −20% precipitation). Two different rate factors are applied (A = 4.6 × 10–15 s⁻¹ kPa⁻³ and A = 2.4 × 10–15 s⁻¹ kPa⁻³). Three different precipitation distributions are applied: CPG = constant precipitation gradient; winter mass balance (b _w) map revised with downscaled precipitation from the WRF model; and LT-DP. The white-shaded horizontal bands indicate the elevation range of the snowline, derived from the MODIS images.

Figure 9a and b show the modelled winter mass balance and the manually interpolated winter mass-balance map, based on the in situ measurements (including the new stakes). There is good agreement between the two maps, both showing the highest winter mass-balance values south of the ice divide. The modelled and measured specific winter balance is given for each outlet in the figure, showing similar values. The mass-balance model was not able to reproduce the abnormally low summer balance of 2010 (Fig. 3b), which was affected by the tephra from the Eyjafjallajökull eruption deposited on the ice cap (Reference GuðmundssonGuðmundsson and others, 2012) and caused increased absorption of shortwave radiation and glacier melt (e.g. Reference BjörnssonBjörnsson and others, 2013). For further validation of the mass-balance model using the LT-DP, the end-of-summer snowline (which is used as a proxy for the ELA, derived from a set of MODIS images from 2007 to 2010, from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a) is plotted on the modelled net mass-balance maps in Figure 9c–f. The location of the MODIS snowline agrees well with the modelled ELA in all four years.

Fig. 9. (a, b) Winter mass balance (b _w) in 2010: (a) modelled using LT-DP and (b) manually interpolated b _w (based on in situ measurements) in m w.e. a⁻¹. The specific winter balance is shown for each glacier: Skálafellsjökull (S), Heinabergsjökull (H) and Fláajökull (F). (c–f) Modelled net balance (b _n) in m w.e. a⁻¹ in 2007 (c), 2008 (d), 2009 (e) and 2010 (f) and the ELA (b _n = 0) drawn in pink. The MODIS end-of-summer snowline (a proxy for the ELA) is shown with black dots (from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a).

Step changes in temperature and precipitation

Steady-state experiments were performed to analyse the sensitivity of the model to step changes in temperature and precipitation relative to the baseline period 1980–2000 (Table 6). In reality, glaciers are constantly responding to climate variations and are never in a steady state, but such simulations provide insight into the sensitivity of glaciers to changes in climate. All simulations start with a geometry that has been run into a steady state. Each model simulation is forced with constant mass-balance grids produced by the mass-balance model. The applied step changes in temperature are in the range of the observed temperature difference between the late 19th century and 2010 observed at Hólar in Hornafjörður (Table 3), and possible future climate scenarios. The modelled glaciers respond to step changes in precipitation and temperature by increasing or decreasing their volume and extent (Table 6). The mass-balance sensitivity to a 1°C temperature decrease is equivalent to a 40% increase in annual precipitation (Table 3), and similarly the sensitivity to a 1°C increase in temperature is close to a 40% decrease in annual precipitation (Table 6).

Table 6. Mass-balance sensitivity of the three outlet glaciers to given deviations from the climate of the baseline period 1980–2000, and the per cent difference between the volume, and area, at the start and end of steady-state simulations, using step changes in temperature and precipitation, relative to the average of the baseline period. The bottom row shows the results of using the average precipitation and temperature of the period 2000–10

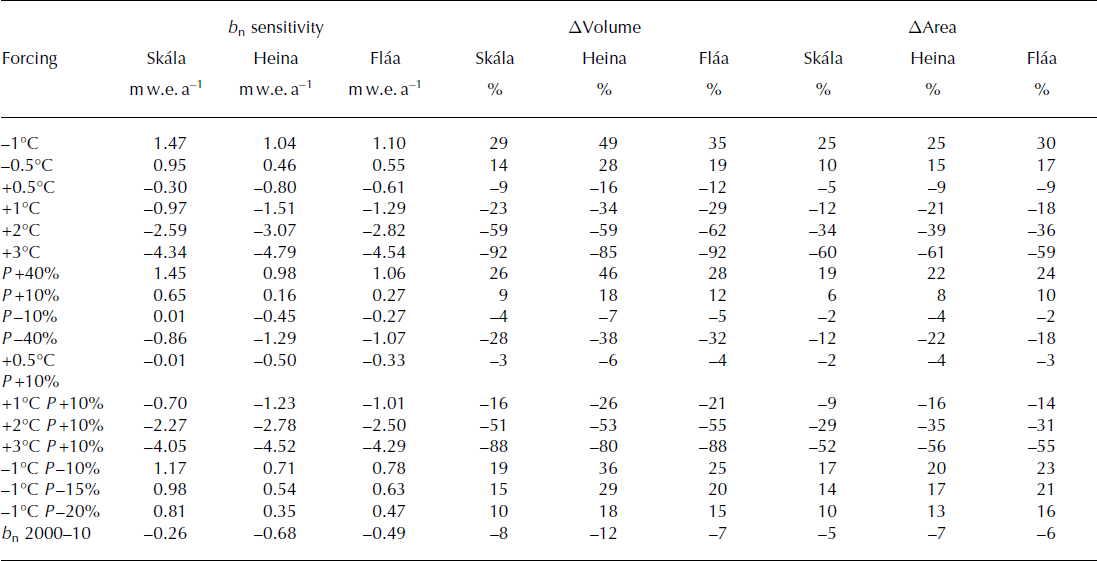
Simulations were made to assess the sensitivity of the glaciers to possible future temperature and precipitation changes, according to predictions for the 21st century in Iceland (e.g. Reference JóhannessonJóhannesson and others, 2007; Reference Nawri and BjörnssonNawri and Björnsson, 2010). Temperature is predicted to increase at a rate close to 0.3°C decade⁻¹ until 2050, and 0.2°C decade⁻¹ until 2100, with superimposed decadal variations determined by natural climate variability (Reference Nawri and BjörnssonNawri and Björnsson, 2010). Changes in precipitation are projected to be moderate, and the increase in annual precipitation from 1961–90 to 2071–2100 is likely to be in the range 0–10% in most regions (Reference JóhannessonJóhannesson and others, 2007; Reference Nawri and BjörnssonNawri and Björnsson, 2010). A 2°C warming and a 10% increase in annual precipitation would eventually lead to >50% volume loss, 8–10 km terminus retreat and up to 35% area loss (Fig. 10b; Table 6). A temperature increase of 3°C and a 10% increase in annual precipitation could lead to 80–90% volume loss (Table 6; Fig. 10c). The glaciers undergo similar volume loss if the annual precipitation is kept the same as in 1980–2000 (Table 6), as a higher percentage of precipitation will fall as rain at higher temperatures.

Fig. 10. (a) The simulated LIA glacier geometry obtained with a constant 1°C cooling and 20% decrease in annual precipitation, relative to the baseline period 1980–2000, and the reconstructed LIA extent in dark blue (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014b). (b, c) The glacier geometry at the end of simulations forced with 10% step increase in annual precipitation and step increase in temperature (b) 2°C and (c) 3°C, relative to the baseline period. The red glacier margin is the result of simulations without any change in annual precipitation, only increase in the temperature, and the lidar margin of 2010 is shown in blue.

Simulating the ∼1890 volume

Model runs were carried out to simulate the reconstructed ∼1890 glacier geometry and volume of the three outlets (as described in Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014b). Temperature measurements, from the late 19th century from Hólar in Hornafjörður (Table 3) indicate 1°C lower temperatures relative to the baseline period. Three different precipitation variants (90%, 85% and 80% of the average annual precipitation of 1980–2000) accompanied by the 1°C lower temperature were applied (Fig. 10). The simulation that best resembles the reconstructed ∼1890 glacier geometry was obtained using a 20% reduction of annual precipitation, which is in accordance with the precipitation estimates over the period 1860–90 (from Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011; Table 3).

The simulated ∼1890 volume of the three outlet glaciers is within the error estimates of the reconstructed (observed) volume derived from geomorphological field evidence (Table 2). The simulated ∼1890 areal extent is slightly smaller than the observed area, except for Fláajökull. The disagreement between the observed and simulated areas can be explained by the small tongues on the west side of Fláajökull, reaching beyond the mapped 1890 glacier margin in the simulations (Fig. 10a). The ELA of the simulated LIA glaciers is around 800 m on Skálafellsjökull, 750 m on Heinabergsjökull and 800 m on Fláajökull, in good agreement with the estimated LIA ELA, which is based on the elevation of the uppermost lateral moraines (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014b). This is a known method, where the lateral moraines are used as a proxy for the ELA, since lateral moraines are only deposited below the ELA, where glacier ice is emerging (e.g. Reference Benn and EvansBenn and Evans, 2010).

Simulating the 1959–2010 evolution

The time-dependent simulations for the period 1959–2010 were initialized with a steady-state glacier geometry, and run both with coupled and uncoupled mass-balance ice-flow models (Fig. 11). The model simulates the observed volume changes well (Fig. 11). The simulations show a slight mass gain in the 1990s, which has also been observed as slight advances of the termini and gain in the glacier surface elevation in the accumulation area (Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a). The observed volume decrease from 2002 to 2010 is not entirely captured by the model, and this is especially noticeable for Heinabergsjökull. The difference between the observed and simulated volumes in 2010 is 9% of the observed 2010 volume. This is larger than the 1.5% and 3.2% differences for Skálafellsjökull and Fláajökull, respectively.

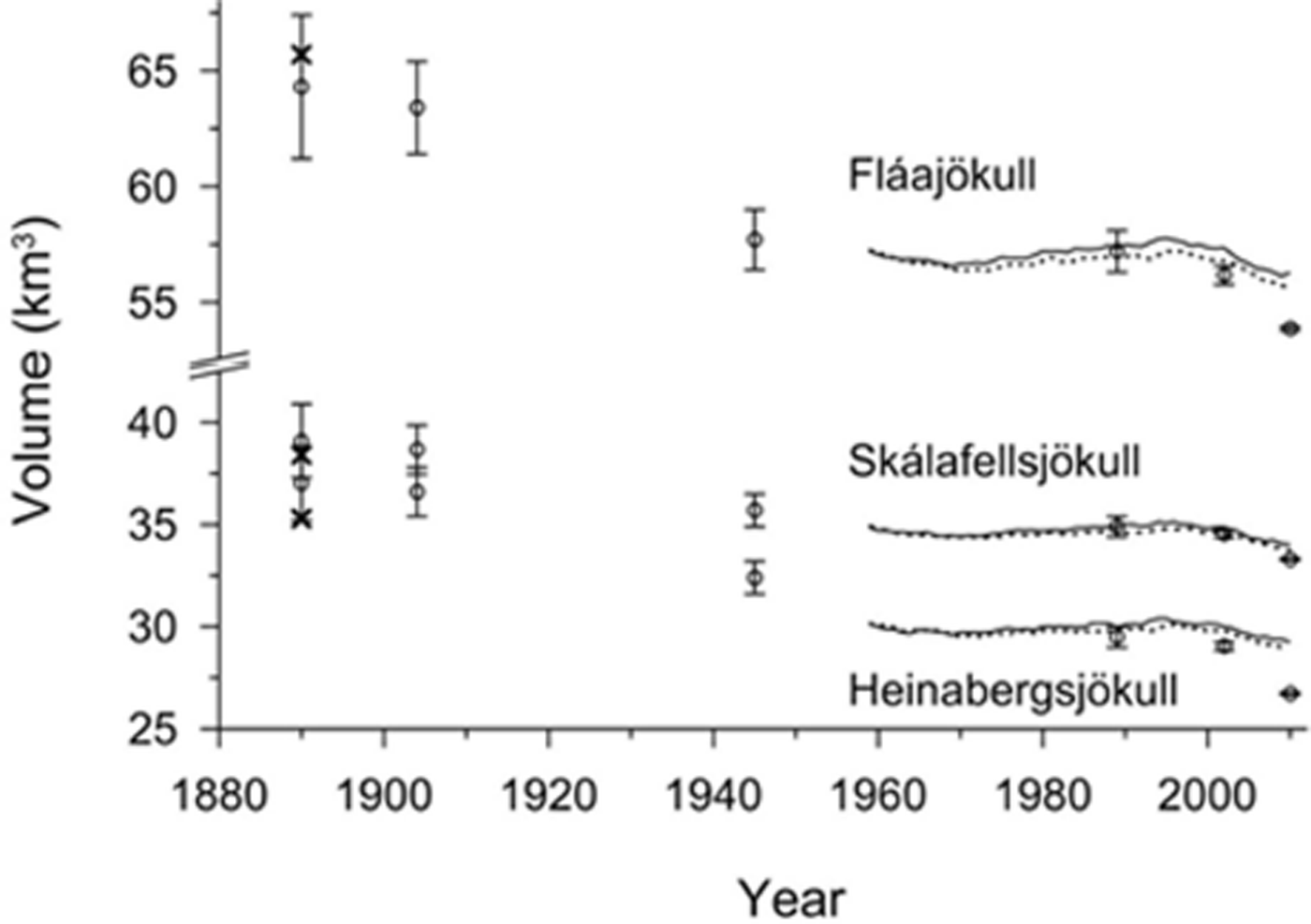
Fig. 11. The volume evolution of the time-dependent simulations, from coupled (dotted lines) and uncoupled (solid lines) runs using the temperature from Hólar in Hornafjörður and LT-DP during the period 1959–2010. The observed volumes of 1890, 1904, 1945, 1989, 2002 and 2010 are shown with open circles (from Reference Hannesdóttir, Björnsson, Pálsson, Aðalgeirsdóttir and GuðmundssonHannesdóttir and others, 2014a). The simulated volume of 1890 is shown with x, assuming that temperatures were 1°C lower than during the baseline period, 1980–2000, and the annual precipitation 20% less (see Fig. 10a for glacier extent).

There is a 1–2% difference in volume between the coupled and uncoupled simulations in the model runs; all glaciers experience greater volume loss in the coupled runs when the mass balance is computed on a lowering surface (Fig. 11; Table 2). This emphasizes the importance of using coupled models for future simulations, when the glaciers will undergo increased surface lowering and retreat, as a result of a warmer climate.

The importance of using downscaled precipitation in the simulations

Located on the southeast coast of Iceland, Skálafellsjökull, Heinabergsjökull and Fláajökull receive high amounts of precipitation in southerly and easterly winds associated with the frequent passage of atmospheric fronts and lows along the coast. From the model simulations it is evident that the precipitation distribution is not adequately described by constant horizontal and vertical precipitation gradients. Orographically enhanced precipitation and snowdrift complicates the snow distribution in the accumulation area of the three outlet glaciers. The two new mass-balance stakes (Skf01 and Fl01) confirm the modelled winter mass-balance pattern of the LT-DP and WRF simulations. Good agreement between the modelled and measured winter balance during the only overlapping year (2010) on the three outlets (Fig. 9a and b) and between the MODIS-derived and modelled ELA (Fig. 9c–f) indicates that the 1 km model resolution is adequate to simulate the precipitation distribution in the complex topography. The 3 km resolution of the downscaled precipitation from the RÁV data is not sufficient for the outlets of southeast Vatnajökull. However, it is adequate to simulate the atmospheric flow and the spatial structure of the precipitation field on the relatively flat Mýrdalsjökull ice cap (Reference Ágústsson, Hannesdóttir, Thorsteinsson, Pálsson and OddssonÁgústsson and others, 2013). This may be attributed to the more complex topography along the southeast coast than in the accumulation area of Mýrdalsjökull.

Constant precipitation gradients may be sufficient when simulating one outlet glacier (as has successfully been done for Hoffellsjökull (Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011)) with more mass-balance data to constrain the model than the three outlets. Modelling a group of outlets separated by steep mountains that influence the orographically enhanced precipitation, however, is more complex. Also, a wealth of data are available for Hoffellsjökull, but not the outlet glaciers for this study. In addition to the mass-balance measurements, data include glacier velocity fields from GPS surveys and satellite data, and energy-balance measurements from an automatic weather station, which were used in the calibration of the mass-balance model (Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011).

The average temperature at Hólar in Hornafjörður in the period 2000–10 was 10.5°C, compared to 9.6°C during the baseline period 1980–2000 (Table 3). Simulations using the average temperature and precipitation of the period 2000–10 result in volume loss of 7–12% (of the 2000 volume) (Table 6), which is less than the volume loss due to a 1°C warming relative to the baseline period (23–34%). Due to this difference, it can be concluded that considerably more precipitation fell in the mountains and on the outlet glaciers of southeast Vatnajökull than was observed at the lowland meteorological stations during the same period. Recent experiments with numerical weather models in this area indicate that changes in precipitation in mountainous terrain are not necessarily correlated with changes in precipitation in lowlands (Reference ÁgústssonÁgústsson, 2014).

Sensitivity of the outlet glaciers to climate perturbations

The importance of precipitation for the mass balance of these outlet glaciers is highlighted when comparing the results of simulations forced with and without a change in precipitation. A 1°C cooling and unchanged precipitation, compared to a 1°C cooling and 20% less annual precipitation, relative to the baseline period 1980–2000, results in a 30–50% increase in ice volume and a 10–18% increase, respectively (Table 6). To counterbalance a volume increase due to a 1°C cooling, the precipitation would need to decrease by ∼40% (Table 6), which is likely outside the range of natural variability. This is similar to previous results of mass-balance modelling studies where increases in precipitation of 20–50% and 30–40% were required to balance increased ablation due to a 1°C temperature rise in a variety of climate regimes (Reference OerlemansOerlemans and others, 1998; Reference Braithwaite and RaperBraithwaite and Raper, 2002). The three outlets respond differently to warming and cooling scenarios (Table 6). Considerable deviations are observed between the modelled and observed surface profiles for Heinabergsjökull in most of the simulations (Fig. 8), whereas there is better agreement between modelled and observed surface profiles for the other two outlets. Heinabergsjökull is more sensitive to changes in temperature and precipitation. For example, the increase or decrease in volume of Heinabergsjökull in response to changes in precipitation and/or temperature is nearly twice that of Skálafellsjökull (Table 6). The hypsometry (area distribution with elevation) and basal topography of these outlets differ. Heinabergsjökull terminates in an overdeepened basin, with a large part of the bed below sea level (Fig. 2a), and its terminus is at low elevation. The proglacial lake of Heinabergsjökull probably affects the mass balance and enhances the ablation by melting and calving, as has been observed and calculated for Hoffellsjökull (Reference AðalgeirsdóttirAðalgeirsdóttir and others, 2011). This additional mass loss is not taken into account in the flow model, as no calving mechanism is included. This can explain the deviation between the modelled and measured ice volumes in the first decade of the 21st century (Fig. 11). The lake area has not increased during the 8 year period. However, the surface topography of the terminus has changed during this period, indicating that the glacier tongue is now floating. A possible change in mean glacier density may also explain why the model does not capture the 2002–10 volume loss, as a constant density is assumed in the simulations.