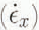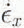Introduction
Crevasses, features that are common to virtually all glaciers and ice sheets, are often interpreted as an indication of tensional stress in surface layers of ice. For example, the crevasses in the upper reaches of an icefall are commonly assumed to represent fast and extending flow. While such assumptions are broadly valid, glaciologists often need a more complete description of the flow field than the current understanding of crevasses allows. A better knowledge of the relationship between crevasses and flow-field dynamics might enable quick and useful assessments of the surface flow conditions to be made from these features. A rough appraisal of the surface flow field would thus be possible for regions of many glaciers and ice sheets. This paper presents a case-study that compares observations of crevasses and detailed measurements of the flow field as a means of investigating the relationship between crevassing and the strain-rate tensor.
The problem of crevassing has been addressed by theoretical, laboratory, and field-based observational studies. At a small scale, work such as that by Reference Rist and MurrellRist and Murrell (1994) and Reference Rist and MurrellRist and others (1994) has examined the orientation of brittle fractures and microcracks in stressed polycrystalline ice. Various workers have addressed the larger-scale problem of crevasse formation in glaciers with force-balance considerations. Much of this work has focused on the fracture mechanics controlling the spacing and penetration depth of crevasses (e.g. Reference LoeweLoewe, 1955; Reference NyeNye, 1955; Reference RobinRobin, 1974; Reference SmithSmith, 1976; Reference WeertmanWeertman, 1977; Reference Nemat-Nasser, Oranratnachai and KeerNemat-Nasser and others, 1979; Reference Sassolas, Pfeffer and AmadeiSassolas and others, 1996). Still other work has addressed the theoretical patterns of crevasse families associated with different flow regimes. For example, Reference NyeNye (1952) described the crevasse patterns that would be expected under various configurations of lateral shear and longitudinal stress.
While some observational case-studies of crevasses have been made (e.g. Reference NyeNye, 1952; Reference Meier, Conel, Hoerni, Melbourne, Pings and WalkerMeier and others, 1957; Reference MeierMeier, 1958; Reference GunnGunn, 1964; Reference KehleKehle, 1964; Holdsworth, 1969b; Reference Colbeck and EvansColbeck and Evans, 1971; Reference Hambrey and MüllerHambrey and Müller, 1978; Reference Hambrey, Milnes and SiegenthalerHambrey and others, 1980; Reference Vornberger and WhillansVornberger and Whillans, 1990), field-based testing of theory has been limited and results have been inconclusive. Previous work has been conducted at a variety of length scales, from measuring the strain field over a few centimeters around a single crevasse (Reference Colbeck and EvansColbeck and Evans, 1971) to modeling the development of kilometer-long Antarctic crevasses (Reference Vornberger and WhillansVornberger and Whillans, 1990). Most field studies have made comparisons of crevasse occurrence with measured values of the principal strain rates. A review of nearly all published field measurements by Reference VaughanVaughan (1993) found that the thermal activation energies for creep and failure appear to be closely related, although no systematic variation with tensile strength was found. Other workers have suggested a value of 0.01 a−1 as the critical level of extending strain rate for the formation of new crevasses in temperate ice (e.g. Reference MeierMeier, 1958; Reference Holdsworth, Bushnell and RagleHoldsworth, 1969a). This, however, has not been well established, as Reference Hambrey and MüllerHambrey and Müller (1978) found new crevasses opening over values ranging from 0.004 to 0.163 a−1.
In addition to the uncertainties associated with crevasse initiation, other questions remain about the relationship between crevassing and flow dynamics. In particular, relatively little research has been directed toward the development of crevasse fields. Does an array of adjacent crevasses represent various stages in the life cycle of a crevasse as it is translated and rotated through the flow field? Or is each crevasse a transient event representing only the stress conditions of its current location? Nye (1983:75) stated, “the crevasses one observes on a glacier have been carried away from the places where they were originally formed and have been rotated by the flow”. For this reason, he suggested that the trajectories of principal stress and strain rate may not necessarily match the crevasse pattern. Holdsworth (1969b) found that a series of transverse crevasses on Kaskawulsh Glacier, Yukon Territory, Canada, are a train with two new crevasses formed at a starting zone each year. Furthermore, Vornberger and Whillans (l990) modeled the translation and rotation of splaying crevasses on lee Stream B, Antarctica, as individual crevasses that persist for decades and are transported tens of kilometers. Yet, open crevasses certainly have a finite lifetime; as ice moves into a changing stress field existing crevasses become relict, while new ones open. Relict crevasses may persist in the new stress regime, may disappear by ablation or infilling with snow and refrozen meltwater, or may close by shear and compressional strains. The questions that remain about the life cycle of crevasses may at least in part be due to a very limited number of comparisons of crevasse fields with high spatial resolution measurements of the flow field.
In this study the problem is addressed with a large observational data sel defining the surface flow field at a short length scale (10—20 m). This allows the strain-rate tensor to be calculated on a grid of densely spaced points with horizontal resolution approximately equal to one-fifth of the ice depth. The pattern of crevasses can therefore be compared with well-defined variations in the flow field. The objective is not to study localized perturbations in the flow associated with the formation of individual crevasses, but to investigate the relationship between families of crevasses and the regional flow field which creates and perhaps maintains them.
The study area covers 0.13 km2 of Worthington Glacier, a temperate valley glacier in the Chugach Mountains, Alaska, U.S.A. (sup>−. The reach is just below the equilibrium-line altitude of the 8 km long, east west running valley glacier and occupies a low-angle bench located between two icefalls. The icefalls are extremely fractured with deep and wide crevasses, multiple fracture directions and numerous seracs, while the bench is characterized by long, narrow and arcuate crevasses spaced 3-10 m apart. The study area extends across the bench from the kinematic center line of the glacier to the north valley wall. Boreholes drilled to the bed and ice-penetrating radar measurements show that ice thickness ranges from 185 to 210 m (Reference Harper, Humphrey, Pfeffer and WelchWelch and others, 1996). Other work on this study reach has addressed the subglacial hydrology (Reference Stone, Meier, Lewis and HarperStone and others, 1994), surface velocity variations (Reference Harper, Humphrey, Pfeffer and WelchHarper and others, 1996) and the characteristics of the bed and subsurface ice (Reference Harper and HumphreyHarper and Humphrey, 1995).

Fig. 1. Map showing Worthington Glacier and the study reach. The study area covers a low-angle bench located between two major icefalls.
Methods
Reference NyeNye (1959) pioneered a procedure for calculating the principal axes of strain rate from measurements of the relative displacement of velocity markers. The methods for calculating the principal axes used here are an adaptation of this approach. A total of 110 point measurements of velocity are interpolated to form a velocity-field grid. Gradients in the velocity field are then used to calculate components of the strain-rate tensor at each of the grid nodes. The velocity gradient method has the advantage of rapid data collection and processing, which enables a large sampling of the flow field. However, the area sampled by this method is less certain than with techniques for direct measurement of deformation within “strain elements”.
Velocities
Surface velocities were measured during two summers by repeated surveys of an array of stakes using a total station theodolite. In the first year, 46 stakes were placed in the 0.13 km2 study reach, and 64 stakes were used in the same reach during the second year. The displacement of the stakes between early May and mid-August (representing the average summer velocity) was used to construct an interpolated velocity field for each of the two summers. Surveying of 17 stakes over a 1-4 year period suggests that the average summer velocity is very close to the average annual velocity. This is due to a balancing effect between a winter slow-down and a spring speed-up.
The interpolated velocity grids are constructed with nodes spaced at 20 m ? 20 m on an orthogonal grid, and are referenced to a local coordinate system. Each velocity grid is smoothed using a Gaussian filler consisting of a 3 ? 3 matrix moved over the grid. This reduces short-wavelength noise in the velocity field which we believe results from localized displacement of stakes caused by movement on crevasses (Reference Harper, Humphrey, Pfeffer and WelchHarper and others, 1996). Again, the objective here is to investigate the regional flow field and associated crevasse patterns, not the localized perturbations associated with any one crevasse. A virtually identical velocity pattern is seen in the two summers’ measurements, and the average difference between the two years at the grid nodes is less than 0.5%. The two velocity grids are therefore combined to form a spatially and temporally averaged velocity field (sup>−. Because stakes are displaced a large distance during the measurement period, the velocity values have a small measurement error: accumulated instrument and measurement error amounts to no more than 0.3% of the velocity. The errors and assumptions associated with the surveying and interpolation procedures are discussed in more detail in Reference Harper, Humphrey, Pfeffer and WelchHarper and others (1996).
Strain rates
The total velocity field (sup>− is decomposed into three orthogonal fields, consisting of the down-glacier (x-direction), cross-glacier (y-direction), and vertical (z-direction) components of velocity: u, v and w, respectively. Differentiation of the horizontal velocity grids gives the strain rates where

The z axis is oriented parallel to gravity, but since the slope of the glacier is low it is also approximately normal to the glacier surface. Therefore, because the air above the glacier can support no shear stress, the z axis is taken to be a principal axis of stress. Assuming that the strain-rate tensor is parallel to the stress tensor and ice is incompressible, the magnitude of the vertical principal strain-rate axis,
![]() 2, is
2, is
The strain-rate fields are next used to calculate the magnitude and direction of the principal strain-rate axes in the horizontal xy plane. The magnitudes of the least tensile of the horizontal axes,
![]() 1, and most tensile of the horizontal axes,
1, and most tensile of the horizontal axes,
![]() 3 are calculated as
3 are calculated as


And

gives Φ, the direction between the y axis and
![]() 1 if
1 if
![]() or
or
![]() 3 if
3 if
![]() y
>
y
>
![]() x
(Reference NyeNye, 1959).
x
(Reference NyeNye, 1959).

Fig. 2. Velocity field. Vectors show the measured displacement of 110 velocity markers during the period early May to mid-August. Contours are of velocity in m year−1. The glacier’s approximate center line is the east-west arm located at y = 5600. Velocities are highest along the center line and decrease toward the valley walls. A strong gradient in velocity is present along the western arm of the center line at the base of the upper icefall.
Two checks on these calculations are possible. One is provided by a direct measurement of the vertical strain rate, w, made at one location (j. Harper, unpublished). The measured vertical strain rate is within 6% of the calculated value of
![]() 2 at this location. A second test on the continuity of the interpolation and numerical differentiation processes is provided by determining the residual, R, of the principal strain rates where
2 at this location. A second test on the continuity of the interpolation and numerical differentiation processes is provided by determining the residual, R, of the principal strain rates where
Since Equation (2) assumes an incompressibility condition, a non-zero value of R implies a lack of continuity in the numerical methods. When compared to the mean magnitude of the greatest principal strain rate,
∈
3, R is found to be negligible over the entire grid: the maximum value of R/
∈
3 at any location is 1.95 ? 10−7. This shows that the numerical methods of interpolation and differentiation of the velocity grids, which are used in finding
![]() 1 and
1 and
![]() 3, are at least internally consistent.
3, are at least internally consistent.
The rotation of ice through the study reach can be tracked by examining infinitesimal elements of ice across the reach. The instantaneous rotation rate,
![]() , is calculated at each of the grid nodes by
, is calculated at each of the grid nodes by

The flow paths are now assumed to be parallel to the x axis. Actual flow vectors deviate from the x direction by a maximum of only 5°, so this assumption produces a minimal error. The rotation is then accumulated as an element of ice passes through the flow field. The total rotation at any one point is calculated from

where a is the distance in the x direction from the up-glacier edge of the study reach.
Several assumptions are built into the above calculations of principal axes and flow rotation. (1) The glacier surface is assumed to be horizontal. All computations are done with horizontal velocity components, and the principal axes are therefore assumed to be in the vertical and horizontal planes. The true surface slope (20 m average) varies from less than 1° to a maximum of about 10° in the extreme southwest part of the reach (x, y ? 4850, 4990). With the exception of this small area, the glacier surface everywhere slopes 3° or less, so this assumption produces a negligible error. (2) The ice is assumed to be isotropic and homogeneous. These properties are necessary for parallelism between the vertical axis of stress and the vertical axis of strain rate. This is a common assumption and is supported by a significant body of literature (e.g. Reference PatersonPaterson, 1994). (3) All gradients in velocity are assumed to be continuous functions of x and y. This is certainly not the ease immediately adjacent to crevasses where jump discontinuities are likely, but is a reasonable representation of the regional flow field. (4) Rotation of a linear feature on the glacier surface is assumed to be represented by the rotation of individual particles. Determining the total deformation (finite strain) of large features in the ice requires complex path integration. However, in this situation where flow is sub-parallel to the x axis and the dominant term in rotation is due to cross-glacier shear (∂u/∂y) the local particle rotation calculated in Equation (7) ran be used to evaluate the rotation of a line of particles (such as a crevasse) on the glacier surface. This method tends to produce an overestimation of rotation for linear features; the more the feature is oriented down-glacier, as opposed to cross-glacier, the greater tile overestimation. As only an upper limit of rotation is sought by these calculations, this result does not affect the interpretations made herein.
Crevasses
A vertical air photograph Fig. 3, which was taken in 1964 at a scale of approximately 1:15000, is used to map crevasses. A photographic record acquired by the United States Geological Survey, covering every few years during the period 1963-93, shows the crevasse pattern to be remarkably consistent over this time interval. The 1964 photo was chosen because this was a year with low snowfall and the crevasses are most visible. The photo was digitized with a high-resolution scanner and then digitally enhanced with non-directional filters to highlight lineations representing crevasses. The mapped crevasse features have widths at the surface ranging from a few centimeters to a few meters, although the image-processing procedure does not allow a distinction to be made between crevasses of different widths. Ground observations suggest that the mapped features are, in fact, open crevasses, and are not simply traces of closed crevasses. Photogrammetric distortion due to relief displacement should be negligible, as the region of interest has low slope and occupies a small area around the principal point of the photo The image is registered to the flow-field coordinate system using points recognizable in the photograph that have been surveyed into the local coordinate system. The error in registration is estimated at ± 15 m.
Results
Flow field
Longitudinal strain rule
The study reach is in transition between longitudinally extending strain fields related to the icefalls above and below the reach (Fig. 4a). While most of the study reach has a longitudinal strain rate of zero or very near zero, two areas aie influenced by the icefalls and have high values of |
![]() x|. One is a region of strong compression in the up-glacier part of the center line (x < 4800). Here, compressional strain rates reach values as high as -0.071 a−1. This area is where the slope of the glacier surface is steadily decreasing as the upper icefall gives way to the low-angle bench of the study reach. The second area with a high |
x|. One is a region of strong compression in the up-glacier part of the center line (x < 4800). Here, compressional strain rates reach values as high as -0.071 a−1. This area is where the slope of the glacier surface is steadily decreasing as the upper icefall gives way to the low-angle bench of the study reach. The second area with a high |
![]() x
| is undergoing longitudinal extension and is in the southeast part of the reach (x > 5000; y < 5600). This area corresponds to a zone of increasing surface slope and has a maximum tensile strain rate of 0.015 a−1. The bed slope is also increasing in this area (Reference Harper, Humphrey, Pfeffer and WelchWelch and others, 1996).
x
| is undergoing longitudinal extension and is in the southeast part of the reach (x > 5000; y < 5600). This area corresponds to a zone of increasing surface slope and has a maximum tensile strain rate of 0.015 a−1. The bed slope is also increasing in this area (Reference Harper, Humphrey, Pfeffer and WelchWelch and others, 1996).

Fig. 3. Vertical air photograph showing the study reach and crevasses. Photograph shows ice surface during the ablation season; white areas are snow patches.

Fig. 4. (a) Contour map of the longitudinal strain rate. (b) Contour map of the shear strain rate. Shaded areas are regions with positive values.
Shear strain rate
Deformation by shearing at the valley walls dominates the surface ice flow of the study reach: a shear gradient is parallel to the valley walls across the entire reach (Fig. 4b). Shear magnitudes increase from near-zero values at the center line to negative values (indicating left-lateral shear) of -0.045 a−1 near the northern valley wall. In addition to the gradient, two areas show localized high shearing. Strongly negative values of
![]() xy
are present in the western arm of the center line (x ? 4825). Here, a steep slope to the southwest causes shear during compression. Positive shear (right-lateral) is present in the southeastern part of the reach (x, y ? 5000, 5525). This area overlaps with the area of high longitudinal extension.
xy
are present in the western arm of the center line (x ? 4825). Here, a steep slope to the southwest causes shear during compression. Positive shear (right-lateral) is present in the southeastern part of the reach (x, y ? 5000, 5525). This area overlaps with the area of high longitudinal extension.
Principal axes
The axes of principal strain rate show significant variations over the study area. The principal axes at each of the grid nodes are plotted as arrows showing magnitude, orientation, and extension or compression (sup>−. No part of the reach shows bulk compression or extension in the horizontal plane, although many areas show a strong disparity in magnitude between
![]() 1 and
1 and
![]() 3. The magnitudes of the principal strain-rate axes reach maximum values of 0.056 a−1 in extension and - 0.084 a−1in compression, while the absolute value averaged over the study reach is 0.02 a−1. Compression is greatest at the western arm of the center line (x ? 4825) where values are as high as -0.084 a−1. Both
3. The magnitudes of the principal strain-rate axes reach maximum values of 0.056 a−1 in extension and - 0.084 a−1in compression, while the absolute value averaged over the study reach is 0.02 a−1. Compression is greatest at the western arm of the center line (x ? 4825) where values are as high as -0.084 a−1. Both
![]() 1 and
1 and
![]() 3 have large magnitudes along the northern edge of the study region where there is strong shearing at the valley margins. A slight peak in the magnitude of
3 have large magnitudes along the northern edge of the study region where there is strong shearing at the valley margins. A slight peak in the magnitude of
![]() 3 is observed in the southeastern part of the reach (x, y = 5000, 5550). This area coincides with the region of high shear and longitudinal extension.
3 is observed in the southeastern part of the reach (x, y = 5000, 5550). This area coincides with the region of high shear and longitudinal extension.

Fig. 5. Axes of principal strain rate plotted to show magnitude and orientation. Values are calculated at the nodes of a 20 m ? 20 m orthogonal grid.
Trajectories
The axes of principal strain rate show an arcuate pattern across most of the study reach (sup>−. The trajectories of the most tensile principal strain rate intersect the northern valley wall at an angle of 40-50° (measured clockwise from the x axis) and curve around to near-longitudinal at the western end of the center line (x, y ? 4850, 5575). South of the center line (y < 5600), the trajectories of
![]() 3 are rotated 180° with respect to the northern part of the reach, The
3 are rotated 180° with respect to the northern part of the reach, The
![]() 3 trajectories thus converge in a zone in the southeastern part of the reach (x, y ? 5025, 5550). Trajectories of the least tensile principal axis intersect the northern valley margin at a 130—140° angle and form an arcuate, concave up-glacier pattern near the margin. In the central and eastern areas of the reach there is an inflection point and the trajectories curve around the center line. Both trajectories become more nearly perpendicular to the valley margin in the down-glacier direction. Trajectories of maximum shear strain, bisecting the intersection of
3 trajectories thus converge in a zone in the southeastern part of the reach (x, y ? 5025, 5550). Trajectories of the least tensile principal axis intersect the northern valley margin at a 130—140° angle and form an arcuate, concave up-glacier pattern near the margin. In the central and eastern areas of the reach there is an inflection point and the trajectories curve around the center line. Both trajectories become more nearly perpendicular to the valley margin in the down-glacier direction. Trajectories of maximum shear strain, bisecting the intersection of
![]() 1 and
1 and
![]() 3 trajectories, are oriented approximately cross-glacier and along-glacier. The exception to the pattern is the western arm of the center line (x < 4825) where trajectories of
3 trajectories, are oriented approximately cross-glacier and along-glacier. The exception to the pattern is the western arm of the center line (x < 4825) where trajectories of
![]() 1 and
1 and
![]() 3 run approximately normal and perpendicular to a steep surface slope located to the southwest of the study reach.
3 run approximately normal and perpendicular to a steep surface slope located to the southwest of the study reach.

Fig. 6. Trajectories of the most and least tensile principal axes. An isotropic point (monstar) in the flow field exists in the southeastern part of the reach.
Rotation
Calculations indicate that rotation is counterclockwise north of the center line and clockwise south of the center line. This is the expected result of shearing at the valley walls. sup>−ur shows the total rotation through the study reach along a cross-glacier transect. Both upper and lower limits on the magnitude of rotation are calculated. The lower limit is based on the average summer velocity, which as noted above is near the annual average velocity. The upper limit is derived by doubling lower-limit values. This is arbitrary but as only an upper limit is sought, doubling should account for the possibility of greater shear strain during times of the year with velocities significantly different than average. Even the upper-limit values of the magnitude of rotation are relatively small: the maximum rotation of any point is only 9°.
Crevasse field
Crevasses are present across the entire study reach (sup>−. The crevasses are of two general types, splaying and transverse. The splaying crevasses form an arcuate, concave up-glacier pattern as they extend from the glacier margin to the center line (y ? 5600). Splaying crevasses intersect the margin at a high angle, and curve to a near-longitudinal orientation at the center line. The splaying crevasses gradually grade into transverse crevasses in the down-glacier direction. By the eastern part of the reach (x > 5000) the crevasses are all transverse. Transverse crevasses intersect the valley margins at a slightly higher angle than the splaying crevasses. Their curvature is concave up-glacier at the glacier margin, but toward the center line they reach an inflection point and begin to have a concave down-glacier orientation. By the center line the transverse crevasses have a near cross-glacier orientation.

Fig. 7. Map showing the traces of major crevasses as mapped from a vertical air photograph. Digital enhancement of the photograph was used te highlight lineations representing crevasses.
The change in orientation of crevasses between an up-glacier transect and a down-glacier transect is shown in Figure 8. Crevasses at the up-glacier transect (x = 4823) have an up-glacier concavity, and their orientation changes from nearly 50° from the x axis at the valley margin to less than 20° at the center line. Crevasses at the down-glacier transect (x = 5103) have a markedly different orientation, with down-glacier concavity and an intersection with the x axis of up to 68°. The change in orientation between the two transects ranges from 10° to 25°.
Field observations reveal that open crevasses generally have sharp edges at the surface, indicating that they have not been exposed to ablation for lengthy time intervals. New crevasses are observed opening, both visually and audibly, throughout the summer season. As bare ice first becomes exposed during the melt season, features that we interpret as relict crevasses are observed. These are arcuate snow-filled troughs, having an approximately triangular cross-section, which are 1-2 m wide and 0.5-1 m deep and extend for tens of meters. These features are cross-cut by fresh new crevasses at angles of 5-10°. By the end of the melt season, ablation has removed all signs of the snow-filled troughs.
Discussion
Rather than long-lived features that are translated and rotated by glacier motion, we believe that the splaying and transverse crevasses of the study reach are short-lived transient representations of local values of the regional flow field. They are translated by the flow on the order of several tens of meters to 100 m, and last no more than 1-2 years. Several lines of evidence support this hypothesis:
-
(1) The strain-rate trajectories and crevasses show a closely matching pattern. Throughout the study area, the crevasses are normal to
 3 (parallel to
3 (parallel to  1). Both crevasses and strain-rate trajectories show similar variations across the study reach; they approach the valley walls at a high angle and show an increase in this angle in the down-glacier direction, and they are concave up-glacier near the valley margin and become concave down-glacier at the center line in the eastern part of the reach (x > 4900).
1). Both crevasses and strain-rate trajectories show similar variations across the study reach; they approach the valley walls at a high angle and show an increase in this angle in the down-glacier direction, and they are concave up-glacier near the valley margin and become concave down-glacier at the center line in the eastern part of the reach (x > 4900). -
(2) The down-glacier change in orientation of the crevasses is not explained by the calculated rotation of the flow field. These values are compared along two cross-glacier transects in Figure 8. Upper-limit values of the calculated rotation are much lower than the observed rotation, suggesting that flow rotation is not responsible for the change in orientation of crevasses between the two transects. As only about 4 years are required for ice to pass from one transect to the other, rotation by flow cannot keep the orientation of a crevasse in accordance with observation for more than about 2 years. The crevasse must close and a new one must open in a differing orientation. This sets an upper limit for the life-span of a crevasse.
-
(3) Field observations of crevasses suggest that they are transient on a 1-2 year time-scale. Active crevasses have fresh, sharp edges revealing little exposure to ablation. Inactive crevasses are cross-cut by younger, active crevasses. While field observations reveal fresh and opening crevasses, mapping does not indicate an increase in the density of crevasses in the down-glacier direction. This implies that old crevasses disappear while new ones open. We suggest that inactive crevasses disappear, when they are no longer oriented normal to the direction of maximum extension, by a combination of closing due to shear strain and surface ablation. Zumberge and others (1960:145) measured closing rates of crevasses on the Ross Ice Shelf that were similar in magnitude to opening rates. Borehole video analysis of the englacial ice structure of Worthington Glacier reveals a large number of clear-ice layers (Reference Harper and HumphreyHarper and Humphrey, 1995) which are probably closed and annealed crevasses.
-
(4) Repeated surveys of stakes at weekly time intervals show-localized anomalies in the velocity field that we believe are the result of ripening and closing of crevasses (Reference Harper, Humphrey, Pfeffer and WelchHarper and others, 1996). These anomalies are equally distributed across the study area, suggesting that crevasses are active everywhere in the reach. The number of these local perturbations is found to be proportional to the average velocity. Thus, as the glacier moves faster the crevasses open and close more frequently, a requirement for continuity of crevasses.

Fig. 8. Observed and calculated rotation. Plot shows the angle between the strike of crevasses and the x axis at an up-glacier and down-glacier transect. Up-glacier is x = 4810; down-glacier is x = 5100. Observed rotation is difference between the two transects. Calculated rotation is shown with error bars representing upper and lower limit values.
An alternative explanation for the differences between the calculated values of flow rotation and the observed rotation of crevasses is that the flow rotation is dominated by strain events that are transient and/or limited in space. Our calculations represent the time-averaged, 20 m length scale flow field, and therefore results contain no information about such time- or space-limited events. However, transient strain events cannot explain field observations that suggest crevasses are opening frequently and have a. short life-span. Furthermore, this explanation would imply that the close correlation between the trajectories of principal axis and crevasse orientation is simply fortuitous.
In addition to indicating the directions of
![]() 1 and
1 and
![]() 3, the crevasse pattern of the study reach contains information about the longitudinal strain rate. Where ϵx
is zero or near zero, splaying crevasses occur. Surface deformation in these regions is dominated by shear. Splaying crevasses extend from the valley walls all the way to the glacier center line, even though the shear strain rate is low at mid-glacier, Reference NyeNye (1952) shows that crevasses are expected to extend to the center line where
3, the crevasse pattern of the study reach contains information about the longitudinal strain rate. Where ϵx
is zero or near zero, splaying crevasses occur. Surface deformation in these regions is dominated by shear. Splaying crevasses extend from the valley walls all the way to the glacier center line, even though the shear strain rate is low at mid-glacier, Reference NyeNye (1952) shows that crevasses are expected to extend to the center line where
![]() x
is zero. Where
x
is zero. Where
![]() x
is compressional (negative), the width of the crevasse belt caused by shear at the valley margin is controlled by the ratio of the shear stress τxy
to the longitudinal stress σx
. If lateral spreading of the ice is prevented by steep valley walls, crevasses can be expected where |τxy
| > |σ
x/✓2|. Reference NyeNye’s (1952) analysis fits the study reach, where crevasses extend to the center line wherever the shear strain rate is greater than the longitudinal strain rate. The effect of negative
x
is compressional (negative), the width of the crevasse belt caused by shear at the valley margin is controlled by the ratio of the shear stress τxy
to the longitudinal stress σx
. If lateral spreading of the ice is prevented by steep valley walls, crevasses can be expected where |τxy
| > |σ
x/✓2|. Reference NyeNye’s (1952) analysis fits the study reach, where crevasses extend to the center line wherever the shear strain rate is greater than the longitudinal strain rate. The effect of negative
![]() x
is to swing most tensile stress around so as to make an angle of intersection with the margin of less than 45°. In the study reach, both crevasses and principal strain-rate axes change from a smaller to a higher angle of intersection with the valley wall as
x
is to swing most tensile stress around so as to make an angle of intersection with the margin of less than 45°. In the study reach, both crevasses and principal strain-rate axes change from a smaller to a higher angle of intersection with the valley wall as
![]() x
goes from negative to zero values. Where
x
goes from negative to zero values. Where
![]() x
becomes positive (extensional) the crevasses change from splaying to transverse.
x
becomes positive (extensional) the crevasses change from splaying to transverse.
The topology of strain-rate fields has been examined in detail by Nye (1983, 1990, 1991, 1993). Nye indicates that an isotropic point, which is a point defined by a pattern of strain-rate trajectories, should be expected in virtually all glaciers. The importance of an isotropic point is that the pattern of strain-rate trajectories around the point is stable to perturbations to the flow field; it may move and war]), but will not disappear. The strain field at an isotropic point is such that
![]() x
=
x
=
![]() y
and
y
and
![]() xy
= 0. The study reach has an isotropic point in the southeastern corner (x, y ? 5050, 5550), which in this case is a monstar pattern (sup>−.This point is along the glacier center line and exists where the value of
xy
= 0. The study reach has an isotropic point in the southeastern corner (x, y ? 5050, 5550), which in this case is a monstar pattern (sup>−.This point is along the glacier center line and exists where the value of
![]() x
changes from zero to a positive value. The crevasses in this region are in transition from splaying to transverse patterns. When the strain-rate field is plotted at a 20 m length scale, the isotropic point covers an area of approximately 2500 m2.
x
changes from zero to a positive value. The crevasses in this region are in transition from splaying to transverse patterns. When the strain-rate field is plotted at a 20 m length scale, the isotropic point covers an area of approximately 2500 m2.
Conclusions
Analysis of data collected on Worthington Glacier indicates that the pattern of crevasses in a non-icefall reach of the glacier contains a great deal of information about the flow field. Crevasses are compared with time-averaged 20 m length scale values of the strain-rate tensor derived from detailed measurements of the flow field. A splaying pattern of crevasses is present where the longitudinal strain rate is compressional or near zero and surface deformation is dominated by shear strain. Where longitudinal extension exists, the crevasses become transverse. Across the entire study area the crevasses are normal to trajectories of the greatest principal extending strain rate. Calculated values of flow rotation for ice moving through the study reach are significantly less than the observed change in the orientation of crevasses from the upstream to downstream ends of the reach. This, combined with field observations, implies that individual crevasses are transient features that exist for no more than about 1—2 years and represent the locally averaged value of the regional flow field. The crevasses of the study reach in Worthington Glacier are, therefore, a useful tool for mapping the strain-rate tensor at the glacier surface. This may be true in reaches of many temperate valley glaciers where surface flow features reflect conditions of relatively fast flow, rapid deformation and strong shear.
Acknowledgements
The work was supported by grants from the U.S. National Science Foundation (OFP-9122916 to W. T. Pfeffer; and OPP-9122966 to N. F. Humphrey). Fieldwork was assisted by B. Welch, D. Bahr and B. Raup, Two anonymous referees gave thoughtful and helpful reviews that improved the manuscript.