Symbols

Introduction
There have been two theoretical analyses of the coupling between a glacier and a soft bed that have reached quite different conclusions. Reference Brown, Hallet and BoothBrown and others (1987) used the sliding theory of Reference LliboutryLliboutry (1979) and a Coulomb-plastic idealization for the rheology of till to study the basal motion of the Fuget Lobe of the Cordilleran ice sheet. They concluded that only ploughing, the dragging of clasts through till, could have reduced the drag on large panicles at the ice/bed interface sufficiently to account for the small basal shear stress inferred from a reconstructed profile of the lobe. Significant pervasive deformation of the bed was thought to be unlikely owing to sand bodies preserved in the till that were either intact or only slightly offset. In contrast, Reference AlleyAlley (1989), using a similar bed geometry and the sliding theory of Reference WeertmanWeertman (1964), concluded that the ice/bed interface beneath Ice Stream B, West Antarctica, should support shear stresses sufficient to deform the bed pervasively, with bed deformation accounting for 60–100% of the basal motion. Although Alley calculated that ploughing might occur over a narrow-range of basal shear stress, he argued that till is best idealized as a viscous fluid and that its effective viscosity is too large to allow a large ploughing velocity without bed deformation.
The analysis presented here is similar to that of earlier studies but benefits from data on local bed shear stresses discussed in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others (1999) and from new field and laboratory data that bear on the rheology of till (Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997; Reference Hooke, Hanson, Iverson, Jansson and FischerIverson and others, 1997, 1998). In addition, ploughing is analyzed differently. For decades, geotechnical engineers have been studying the forces on cones, plates and piles as they are pushed downward through water-saturated fine-grained sediment. Herein, a relation derived from these studies is applied to the similar problem of particles in basal ice dragged through a yielding till substrate.
The overall goal of this paper is to determine whether a safe generalization is possible regarding the dominant basal flow mechanism of glaciers on soft beds. Models of ploughing and sliding provide the basis for calculating a relation between the effective pressure and shear stress on the bed, and the results are compared with those from Storglaciären, Sweden (Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999, Fig. 11). The processes that lubricated the base of Storglaciären sufficiently to preclude significant deformation of the bed are explored, together with the sensitivity of this lubrication to variables such as the bed roughness and the thickness of the water layer at the ice/bed interface.
Bed Idealizations
Although penetration testing through boreholes has suggested that the bed of Storglaciären is probably free of till in places (about 5% of boreholes are underlain by an impenetrable substrate), the goal here is to analyze the coupling between ice and the underlying till for comparison with the empirical record derived from the tiltmeter signal discussed in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others (1999). Therefore, only the till portion of the bed is considered, keeping in mind that sticky spots of some kind elsewhere seem to support the major part of the basal shear stress, particularly when basal water pressure is high. To estimate the shear stress that can be sustained by the bed due to the combined action of sliding and ploughing, both the surface roughness and rheology of the bed must be considered.
Bed roughness
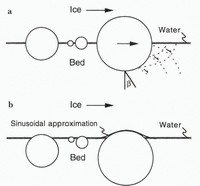
The till bed is rough due to particles that protrude, to varying extents, into the sole of the glacier. As in other studies (Reference Brown, Hallet and BoothBrown and others, 1987; Reference AlleyAlley, 1989), herein particles are idealized as spheres centered on the ice/bed interface (Fig. 1a). The bed, therefore, consists of an array of isolated hemispherical bumps of different sizes. If there is no sorting of particles at the bed surface, a reasonable first approximation, then the distribution of bump sizes reflects the grain-size distribution of the till. The grain-size distributions of basal tills are approximately self-similar, and thus, the number, N R , of bumps of radius R can be expressed as a continuous function in terms of a fractal dimension, d:

where N 0 is the number of particles of reference size R 0 (Reference Hooke and IversonHooke and Iverson, 1995). Although d is a crude measure of a grain-size distribution, it provides a compact and hence convenient means of characterizing the gross granulometry of till.

Fig. 1. Two idealizations of the ice/bed interface. (a) Particles centered on the bed surface form hemispherical roughness elements. Dashed lines are slip surfaces in the till bed that dip at an average angle b. (b) Particles buried in the bed form roughness elements that approximate sinusoids.
The bed, however, may be smoother than the above idealization suggests. As ice melts at the bed it should exert a downward drag on particles that protrude into the glacier sole (Reference HalletHallet, 1979; Reference IversonIverson, 1990). Particles that are near the transition size of sliding theories, and hence subject to the largest drag stresses, may be pushed into the bed to depths well past their center lines, particularly during periods of low effective pressure when the bed is especially weak. Thus, sinusoids may approximate the resultant subdued bumps on the bed better than hemispheres (Reference Brown, Hallet and BoothBrown and others, 1987). A second model of the bed is also considered, therefore, that consists of sinusoids with wavelengths equal to 2R and amplitudes that are a constant small fraction of R (Fig. 1b).
An important factor controlling the effective roughness of the bed is the thickness of the water layer that is expected between the ice and sediment (Reference Brown, Hallet and BoothBrown and others, 1987; Reference AlleyAlley, 1989). This layer submerges the smallest particles, thereby reducing the area of the bed in contact with ice.
To determine the submerged fraction of the bed, f, as a function of the thickness of the water layer and the grain-size distribution, note that
where n is the sediment porosity, A s is the area of all particles submerged in the water layer (not including void space) and A b is the total area of the bed. To first determine A s, notice that particles of radius R occupy an area of the bed. A R = N R πR 2. Substituting Equation (1) into this equation yields
where C = πN 0 R 0 -d . Integrating Equation (3) from zero to a water-layer thickness, d w, yields the area of particles submerged in the film:

To determine A b in Equation (2), note that the area of the bed, A Rv, occupied by a given size class and adjacent void space, is A Rv = ? R (1 – n)-1, assuming that, on average, void space scales linearly with the particle size. Substituting Equation (3) into this equation and integrating from zero to the upper fractal limit of the grain-size distribution, R u (the largest particle size that contributes to the till roughness), gives

Substituting Equations (3) and (5) into Equation (2) yields the submerged fraction of the bed:

Thus, as d approaches 3.0, as is the case for size distributions with a high proportion of clay and silt (Reference Hooke and IversonHooke and Iverson, 1995), f approaches 1.0. In principle, values of d greater than 3.0 are not possible, and fits to data that yield such values indicate that either all or part of the size distribution is not fractal.
Till rheology
An analysis of ploughing requires that the till rheology be characterized. Both Coulomb-plastic and viscous assumptions have been made for till. If till is fundamentally a viscous fluid, then the force exerted on ploughing particles by till should increase with the speed of the particle. Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others (1997) measured the force on ploughmeters (Reference Blake, Fischer and ClarkeFischer and Clarke, 1994) and dragometers (Reference Iverson and JanssonIverson and others, 1994) dragged through till beneath Storglaciären. The former is a near-vertical steel rod that is dragged through till at the bottom of a borehole; the latter is a short cylinder with conical ends that is pulled through the till bed with its long axis parallel to the bed. The basal water pressure and glacier surface velocity were also measured. As increases in water pressure accelerated the glacier and forced the dragometer and ploughmeter through the till at increased speeds, the force on tile instruments decreased rather than increased. Thus, there was no evidence that the till strengthened in response to increased strain rates adjacent to the instruments. Similarly, rate-controlled ring-shear tests have indicated that the ultimate strength of till is essentially independent of the rate of deformation (Reference Fischer, Iverson, Hanson, Hooke and JanssonIverson and others, 1998).
Thus, the till is best idealized for this problem as a Coulomb-plastic material, in which the ultimate (steady) strength of the till, τ u, is considered to be independent of the rate of deformation. Therefore, τ u = c i + P e tan φ u, where φ u and c i are the ultimate friction angle and cohesion intercept (Reference Lambe and WhitmanLambe and Whitman, 1979, p. 308), respectively, indicated by laboratory tests, and P e is the effective pressure (the latter is defined as P i – P w, where P i is the ice-overburden pressure and P w is the basal water pressure). This relation obviously does not rule out the possibility of apparent viscous effects, like the distributed strain that has sometimes been observed in till beneath valley glaciers (e.g. Reference Boulton and HindmarshBoulton and Hindmarsh, 1987). Nor does it depart significantly from exponential relations (Reference KambKamb, 1991; Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997) supported by laboratory lests on clays (e.g. Reference MitchellMitchell, 1993, p. 343), in which the sediment strength is only weakly dependent on the rate of deformation.
Flow Mechanisms
Sliding
The drag exerted on some particles by regelation and ice creep will be less than that required to push the particles through the substrate. Thus, these sliding mechanisms will limit the local shear stress on such particles. Following Reference Brown, Hallet and BoothBrown and others (1987), the drag for the case of hemispheres centered at the bed surface is estimated using the sliding theory of Reference LliboutryLliboutry (1979). For the case of Glen’s flow law, stationary particles and no ice/bed separation,
where U is the sliding speed, τ s is the shear stress associated with sliding, and ? 1 and C 1 are material constants for clean temperate ice. As is familiar, creep of ice contributes most to sliding past large particles, and regelation dominates motion past small particles. Owing (o the non-linearity of the flow law of ice, the transition particle size, R *, depends on U:
where units are meters and years.
Water-filled cavities are expected down-glacier from particles if the basal water pressure exceeds the pressure that ice exerts on lee surfaces. For hemispherical bumps, Lliboutry (1979, p. 81) noted that this is roughly equivalent to assuming that cavities form when the shear stress τ s exceeds the effective pressure, P e (sec Appendix). Thus, substituting P e for τ s in Lliboutry’s sliding relation (Equation (7)) and multiplying by R yields a quadratic equation with roots that define the radii of the largest and smallest particles for which cavities are expected:

Particles with radii outside this range will be accommodated Coo easily by regelation or creep to satisfy τ s > P e.
To obtain an estimate of the shear stress on a hemispherical bump with a cavity, τ c, Lliboutry assumed, as simplifying approximations, that cavities extended over the full leeward half of hemispheres and that these cavities did not influence stresses on stoss surfaces. As shown in the Appendix, the local shear stress, τ c, is then

(Reference LliboutryLliboutry, 1979, equation (47)). Thus, for those particles with cavities, this equation is expected to provide a better estimate of the shear stress associated with sliding than Equation (7).
To calculate the drag on the uppermost surfaces of buried particles, modeled as sinusoids, the theory of Reference NyeNye (1969) is used. For a single sine wave, a sin k 0 x, and assuming no ice/bed separation.

where k 0 = 2π/wavelength, and η is the viscosity of ice. In reality, the effective viscosity of ice depends on U. The creep term of this equation, thus, is likely to be a poorer approximation than that of Equation (7) for the case of hemispheres. In addition, Equation (11) is strictly appropriate for a bed that is wavy in only one direction. However, for the parameter values considered by Reference NyeNye (1969) a bed consisting of two superimposed sine waves at right angles increased τ s for a given sliding velocity by only 18%.
Ploughing
Particles will be dragged through the substrate (plough) if the force on them that can be exerted by sliding ice exceeds the resistive force offered by till. The speed of a ploughing particle relative to the ice will be adjusted such that the drag exerted by ice equals that exerted by the till.
Studies of cone, plate and pile penetration through water-saturated fine-grained sediment provide clear guidance for assessing the magnitude of the resistive force. In a cone-penetration test (e.g. Reference Durgunoglu, Mitchell and BromsDurgunoglu and Mitchell, 1974; Reference De Ruiter, Verruijt and BeringenDe Ruiter, 1982; Reference McNeilan, Bugno, Chaney and DemarsMcNeilan and Bungo, 1985), for example, a shaft with a cone on its end is driven downward through sediment at a constant rate, and the force on the cone is measured. From this force, the shear strength of the sediment can be estimated as a function of depth. It is worth noting that Coulomb-plastic behavior is usually assumed in such studies because tests at variable rates indicate only slight strengthening of sediment with large increases in the rate of penetration (Reference De Ruiter, Verruijt and BeringenDe Ruiter, 1982; Reference Poskit, Leonard, Verruijt and BeringenPoskit and Leonard, 1982). Indeed, in such studies the rate effect of concern is more often weakening of the sediment that occurs if penetration rates are sufficiently high to generate pore pressures in excess of hydrostatic beneath the cone (e.g. Reference Campanella, Robertson and GillespieCampanella and others, 1983).
Of the many models used in penetration testing, that of Reference Senneset, Janbu, Chancy and DemarsSenneset and Janbu (1985) is most appropriate for this problem because it is explicitly formulated in terms of the effective pressure and is broadly applicable to ploughing elements of different shapes. Consider the lower half of a spherical particle ploughing through the bed (Fig. 1a). Sediment down-glacier from the particle yields plastically in compression along conjugate slip surfaces oriented at an average angle ß with a normal to the bed. The bed-parallel force, F p, on the leading surface of the particle is given by

where P el is the local effective pressure on the till immediately down-glacier from the particle, c is the cohesion, φ is the friction angle, A c is the cross-sectional area of the particle below the bed surface, and N F is a dimensionless bearing-capacity factor:

(Reference Janbu, Senneset and BromsJanbu and Senneset, 1974; Reference Senneset, Janbu, Chancy and DemarsSenneset and Janbu, 1985).
There is good empirical support for Equation (12). Reference Senneset, Janbu, Chancy and DemarsSenneset and Janbu (1985) found that it yielded friction coefficients from cone-penetration data on silty, sandy clay that were in good agreement with independent triaxial tests on core samples. Similarly, Reference Iverson and JanssonIverson and others (1994) found good agreement between forces calculated from Equation (12) and those on cones dragged through till in the laboratory.
As long as F p is non-zero, there will be ice motion past the particle, and the local ice pressure on the bed down-glacier from the particle will be less than the ambient ice pressure. Thus, the local effective pressure down-glacier from the particle, P el, should be less than the ambient effective pressure by an amount kτ p, where τ p is the shear stress on the ploughing particle, and k is a “pressure-shadow factor” that depends on whether regelation or creep is the dominant mechanism of ice motion (Reference Brown, Hallet and BoothBrown and others, 1987). Therefore,
Noting that F p = τ p πR 2 and A c = πR 2/2, substituting Equation (14) into Equation (12), and rearranging yields τ p in terms of P e, k, and measurable properties of the till:

Unlike the driving stress on particles associated with sliding, the shear stress required for ploughing is independent of the particle size and speed.
An important uncertainty associated with Equation (15) is that ploughing particles may well encounter particles of similar size, hence violating the assumption that the surrounding till behaves as a continuum. For example, ploughing particles as small as 0.2 mm are considered subsequently, and such particles should have many neighbors of similar or larger size. However, this problem should be minimized, to some extent, because larger particles should plough at higher speeds than smaller particles. The transition particle size indicated by the Lliboutry sliding theory (Equation (8)) is on the order of centimeters for the sliding speeds at Storglaciären considered hereafter. Thus, the relative velocity between the ice and such particles will be small, which requires that these particles plough rapidly through the bed at near the speed of the ice. Smaller particles, however, are accommodated more easily by regelation, and hence, ice should move past them more rapidly, resulting in smaller ploughing speeds. At least in principle, therefore, sand-sized ploughing particles should seldom collide with particles on the bed surface that are of similar or larger size. It should also be noted that regardless of the relative sizes of interacting particles, friction between grains dominates the resistive force. Equation (15) is essentially a friction law, and thus, although it likely becomes a less accurate approximation when similar-sized particles interact, it may still adequately characterize the physics of the resistive force.
Another important qualification regarding Equation (15) is that it is appropriate only if the pore-water pressure of the till is not perturbed significantly down-glacier from a ploughing particle. It is possible, however, that the rate of till compaction there might exceed the rate at which pore pressure can diffusively dissipate (Reference Iverson and JanssonIverson and others, 1994), In that case, pore pressure would be in excess of the ambient value, and the till might weaken substantially. The cone-penetration data of Campanella and others (1983, Fig. 1) demonstrate this important effect so clearly that their data are reproduced in Figure 2. The magnitude of the pore-pressure excess should scale inversely with the dimensionless parameter r (adapted from Reference Iverson and LaHusenIverson and LaHusen, 1989):
where k p is the hydraulic permeability of the till, U p is the ploughing speed, α is the till compressibility, μ is the dynamic viscosity of water at 0°C (1.78 × 10-3 Pa s), and δ is the characteristic length of the zone of compression in front of the particle. The parameter r is the ratio of the time-scale for generation of excess pore pressure (δ/U p) to the time-scale for diffusive pore-pressure equilibration across δ (δ 2 αμ/k p).

Fig. 2. Results of a cone-penetration test (from Reference Campanella, Robertson and GillespieCampanella and others, 1983). The dashed line in the center diagram is the hydrostatic pore pressure, and u is the excess pore pressure generated adjacent to the cone. Note how the. stress on the cone (bearing resistance) decreased markedly as excess pore pressure developed in the impermeable clayey silt layer. The speed of the cone was steady at 0.02 m s-1.
Equation (16) can be used to estimate the range of particle sizes over which Equation (15) is valid because the value of δ is approximately equal to the diameter of the ploughing particle, as indicated by laboratory studies of cone penetration (Reference Malyshev, Lavisin and BromsMalyshev and Lavish, 1974; Reference Koumoto, Kaku, Verruijt and BeringenKoumoto and Kaku, 1982). The threshold value for r, below which excess pore pressure should develop, can be estimated from the cone-penetration study of Reference Campanella, Robertson and GillespieCampanella and others (1983), in which all relevant parameters were either measured or estimated reliably. Using this study, Reference Iverson and JanssonIverson and others (1994) found that for values of r less than 1.5, detectable excess pore pressures are likely to develop. The rate of sliding, which should approximately equal U p, seldom exceeds 0.10 m d-1 beneath Storglaciären. The till, relative to many tills, is quite permeable, k p = 1.3 × 10-14 m2. Over a wide range of confining pressure, the till compressibility is about 3 × 10-7 Pa-1, based on consolidation tests with our ring-shear device (Reference Fischer, Iverson, Hanson, Hooke and JanssonFischer and others, 1998). With these parameter values, Equation (16) indicates that significant excess pore pressures should not arise in front of ploughing particles of any reasonable size (< 14 m) beneath Storglaciären, However, beneath more rapidly sliding glaciers with less permeable and more compressible basal sediment (virtually any till that contains significant clay minerals), this effect may be important, as examined subsequently for the case of Ice Stream B.
Calculation of τsp
The objective now is to calculate the shear stress that the bed can sustain due to the combined action of sliding and ploughing, τ sp. If τ s < τ p, sliding limits the shear stress, and particles are stationary. If τ s > τ p, there is still sliding of ice past particles, but ploughing limits the shear stress, and panicles move through the bed at some fraction of the sliding speed. For the case of no ice/bed separation, τ s (Equation (7)) and τ p (Equation (15)) are calculated, and the smaller of the two values is chosen for the local shear stress, τ i, supported by particles of size class i. If ice/bed separation is allowed, τ c (Equation (10)) is used rallier than τ s for those size classes that should have cavities in their lee, as determined from Equation (9). The value of τ sp, for a given effective pressure and sliding speed, is the sum of the shear stresses on the individual size classes, adjusted to account for the fraction of the bed, A if, occupied by each size class:

Only size classes in which R exceeds the thickness of the water film are included in the summation. Integrating A R (Equation (3)) from R i to R i+1 and dividing by A b (Equation (5)) yields

Superposition of stress fields in both the ice and the till adds uncertainty to the calculation. For the case of regelation past a square array of equal-sized cylinders in mutual contact, the drag on a single cylinder is reduced by 45% over the case of an isolated cylinder (Reference PhilipPhilip, 1980). For the case of linear creep past arrays of spheres, the drag on a single sphere may be reduced by as much as a factor of 10 (Reference Brown, Hallet and BoothBrown and others, 1987). The drag exerted on ploughing particles by till may also be reduced by the superposition of stress fields (Reference AlleyAlley, 1989), although the tendency for strain to localize near ploughing tools (Reference Malyshev, Lavisin and BromsMalyshev and Lavisin, 1974; Reference Koumoto, Kaku, Verruijt and BeringenKoumoto and Kaku, 1982) should help minimize this effect. Despite potentially large errors caused by stress-field interference, no attempt is made here to account for it quantitatively. Doing so would add adjustable parameters to the analysis that cannot be estimated reliably and thus would be of little value.
Water-filled cavities that extend down-glacier from the leeward sides of particles may submerge other particles, which adds uncertainty to Equation (17). However, many such cavities would tend to approximate a film of non-uniform thickness over the bed. The chosen film thickness can, therefore, be viewed as a gross parameterization for the extent of cavity formation in the lee of particles.
Parameter Choices
To calculate the shear stress due to sliding and ploughing over a range of effective pressure, the geometrical properties of the bed (d, n, d w, R u). the physical properties of the ice and sediment (B 1, C 1, φ ß, c), the pressure-shadow factor, k, and the variation in sliding speed, U, with effective pressure must be measured or estimated.
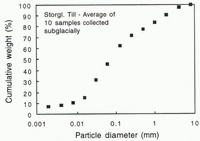
The average grain-size distribution of the Storglaciären till, determined from discrete weight fractions of ten disturbed but unwashed samples collected subglacially through boreholes, is shown in Figure 3. The distribution is approximately fractal, and the value of the fractal dimension d is 2.92 (Reference Hooke and IversonHooke and Iverson, 1995).
Taking d = 2.92 yields a variation in the submerged fraction of the bed with water-layer thickness (Equation (6)) that is quite similar to the approximation of Reference AlleyAlley (1989) for water-layer thicknesses greater than ~0.1 mm (Fig. 4). The water-layer thickness at Storglaciären has been estimated by Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others (1997), using the difference in water pressure recorded by a sensor in a borehole and one inferred to be at the ice/till interface a few meters away. The pressure difference, together with the calculated basal melt rate, indicated a water layer 0.1–0.2 mm thick. The water-layer thickness assumed here is 0.2 mm.
The upper fractal limit of the particle-size distribution, R u, is constrained by the till thickness. The till at the site of the tiltmeter could not be penetrated more than 035 m. On that basis, R u = 0.10 m is assumed. The sediment porosity is taken to be 0.35.
The values chosen for the rheological parameter, B 1, and the regelation parameter, C 1, are those for clean glacier ice (Reference LliboutryLliboutry, 1979, table 1). A suite of ring-shear tests have been conducted on the Storglaciären till at different confining pressures to determine the ultimate friction angle, φ u. The shearing rate was steady (50 mm d-1) and comparable to the speed of Storglaciären. These tests indicated that φ u = 26.3° (Reference Fischer, Iverson, Hanson, Hooke and JanssonIverson and others, 1998). This is the appropriate value for the effective friction angle, φ, during ploughing because till should often undergo sufficient strain as it deforms around panicles to reach its ultimate strength. This should be especially true for larger particles near the transition size of the sliding theory, which are those most likely to plough True cohesion is thought lobe absent in the Storglaciären till (Reference Fischer, Iverson, Hanson, Hooke and JanssonIverson and others, 1998). Thus, c = 0, and Equation (15) reduces to only a fractional term.

Fig. 3. Average grain-size distribution often till specimens collected from the bed of Storglaciären through boreholes.
The orientation of slip surfaces in the sediment given by the angle ß depends on the sediment compressibility and particle size and is insensitive to the geometry of the ploughing object, Experiments with cones, plates and piles indicate that ß = 15° for compressible fine-grained sediment like till (Reference Janbu, Senneset and BromsJanbu and Senneset, 1974; Reference Senneset, Janbu, Chancy and DemarsSenneset and Janbu, 1985). In principle, ß should vary with the effective pressure, but engineers have found empirically that this dependence can usually be neglected.
The value of the pressure-shadow factor, k, depends on whether ice flows past particles primarily by regelation or by creep. Reference Brown, Hallet and BoothBrown and others (1987) calculated values of about 0.1 and 0.4 from regelation (Reference NyeNye, 1967) and creep (Reference Lliboutry and RitzLliboutry and Ritz, 1978) theory, respectively. These values were based on an average of the normal stresses that ice should exert on the bed along the midline of the failure surface in the till. This average is approximately the same as that expected from the failure surfaces considered in this analysis (Fig. 1a). Thus, the values of k used by Brown and others arc-adopted here. For a given particle size and sliding speed, the transition particle size (Equation (8)) is used to determine whether regelation or creep dominâtes How, and the value of k is assigned on that basis.

Fig. 4. The submerged fraction of the bed, f, as is assumed in the model, in which Ru = 0.1 m and n = 0.35, and for the case of Ru = 1.0 m and n = 0.30 to allow a comparison with the approximation of Reference AlleyAlley (1989).
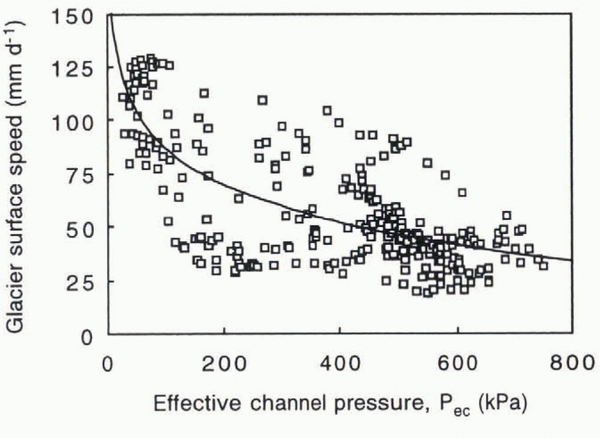
To calculate the shear stress that can be exerted on particles by sliding, τ s, from Equation (7) or (11), the variation in U with effective pressure must be known. From the data presented in Iverson and others (1999, Fig. 8), the glacier surface speed is plotted in Figure 5 as a function of the effective channel pressure, P ec. The wide scatter of points is best fit with a logarithmic relation that is qualitatively similar to the power-law relations determined over longer time-scales at Storglaciären (Reference Iverson, Hanson, Hooke and JanssonJansson, 1995) and elsewhere (Reference Iken and BindschadlerIken and Bindschadler, 1986). Borehole inclinometry indicates that internal deformation accounts for about 10 mm d-1 of the surface speed (Reference Hooke, Pohjola, Jansson and KohlerHooke and others, 1992). Subtracting this value from the surface speed yields the best-fit approximation, U = 198 – 60 log P ec, where U is in mm d-1 and P ec is in kPa.
Results
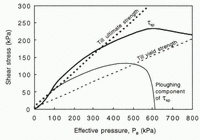
The model of the bed consisting of hemispherical bumps, with and without leeward cavity formation, is considered first. To illustrate the relative importance of ploughing and sliding as a function of particle size, τ p/τ s (dashed lines) and τ p/τ c (solid lines) are plotted in Figure 6a. Values of these ratios that are less than 1.0 indicate that the drag on the particle by ice will exceed the strength of the till bed. Thus, the particle will plough, and the shear stress on the particle will be limited by ploughing, rather than by sliding. Reductions in effective pressure, P e, increase the number of size classes that plough, owing to the resultant decrease in till strength and the associated increase in glacier sliding speed (Fig. 5). The latter increases the potential driving stress on particles. For the range of P e considered in Figure 6a, all particles greater than 2 mm in radius support shear stresses limited by ploughing. Since this is below the transition bump size (Equation (8)), shear stresses on all size classes are limited by either ploughing or regelation. Creep of ice is expected, but only around the largest particles, which plough and support shear stresses limited by the strength of the till.
Ploughing limits the local shear stress over most of the fraction of the bed that is not submerged by the water layer (Fig. 6b). For P e <12 kPa, all particles in contact with ice plough and constitute 28% of the bed area; the rest of the bed is submerged by the water layer. Regelation becomes increasingly important at higher values of P e because the till is stronger and driving stresses are smaller due to the reduced sliding velocity, both of which suppress ploughing.
In Figure 6c, calculated values of the shear stress due to sliding and ploughing, τ sp, are compared with local shear stresses determined from the tiltmeter record described in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others (1999). Values determined from the tilt-meter record are appropriate for comparison because it is believed that the till never deformed at its ultimate strength at the site of the tiltmeter, and thus, that shear stresses were controlled entirely by ploughing and sliding, rather than by bed deformation. The data, therefore, constitute an empirical record of τ sp. Results from Iverson and others (1999, Fig. 11b) are used for comparison because they are based on the best estimate of the till yield strength (50% of the ultimate strength; Reference Ho, Vela, Jenson, Clark, Sheahan and KaliakinHo and others, 1996).
The model predicts the observed increase in τ sp with P e. This reflects the importance of ploughing: at higher values of P e the till is stronger, and ploughing particles support larger shear stresses.

Fig. 5. Relation between glacier surface speed and effective channel pressure measured at Storglaciären with a logarithmic best fit to the data (plotted from the records of surface speed and water pressure in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999, fig. 8). The correlation coefficient is 0.72. Linear and power-law fils were poorer.
The model, however, overestimates τ sp and predicts, in contrast with the data, that the τ sp curve should be concave downward (Fig. 6c). The latter effect is a consequence of the change in partitioning between ploughing and regelation. With increasing P e, the drag stresses on Stationary particles accommodated by regelation are reduced, due to the reduction in sliding speed. Thus, because regelation limits the shear stress over a progressively larger fraction of the bed as P e increases, the rate of increase in τ sp is reduced at higher values of P e.
Given that a bed idealized as hemispherical bumps results in an overestimate of τ sp, there is some motivation for considering now the smoother bed consisting of particles that protrude only slightly into the glacier sole (Fig. 1b). If it is assumed that there is no ice/bed separation in the Ice of particles, the value of τ s is given by Equation (11). Since particles are assumed to be buried at depths [last their center lines, τ p is no longer given by Equation (15). Rather it is increased by the factor, 2A c/πR 2, the ratio of the cross-sectional area of the particle below the bed (A c) to that if the particle were centered on the bed (πR 2/2). For a representative case in which particles form sinusoids of amplitude 0.2 R and wavelength 2R, the ratio, τ p/τ s is an order of magnitude larger than for the case of the rougher bed (Fig. 6d). This is due to both the reduction in driving force on particles exerted by sliding ice and an increase in resistive force caused by the deeper burial of particles. Relative to the case of the rough bed, regelation limits the basal shear stress over a larger fraction of the bed area that is not submerged in the water layer (Fig. 6e).
Interestingly, τ sp is larger for the case of the smoother bed (cf. Fig. 6f and c). This is because, at the low effective pressures considered here, ploughing is the dominant stress-limiting flow mechanism, and the process is impeded by the nearly complete burial of particles. Thus, smoothing the bed worsens rather than improves the agreement between the model results and the data.
It might be argued that only particles near the transition size of sliding theories should be pushed into the bed, owing to the greater bed-normal drag exerted on such particles by ice melting at the bed. To explore this idea, roughness elements were again idealized as hemispheres, and the upper fractal limit was assumed la be 0.01 m, rather than 0.1 m, to account for complete burial of the largest size fractions. Although this decreases the magnitude of τ sp, bringing the data and model results into better agreement, the form of the calculated relation is, again, not like that observed (Fig. 7).

Fig. 6. (a) Values of τp/τs (dashed lines) and τp/τc (solid lines) as a junction of grain-size for a bed consisting of hemispheres. (b) Fractional area of the bed occupied by ploughing particles and by stationary particles accommodated by revelation for a bed consisting of hemispheres. (c) Calculated values of τsp (thick lines) for a bed consisting of hemispheres compared with shear stresses determined from the tiltmeter record discussed in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others (1999). Shear stresses computed from the tiltmeter record are based on the assumption that the till yielded at 50% of the ultimate strength (e.g. Reference Ho, Vela, Jenson, Clark, Sheahan and KaliakinHo and others, 1996), with F = 0.07 as described in Iverson and others (1999, fig. 11b). Shear stresses based on the yielding of the till at 25% of the ultimate strength (F = 0.32) are smaller, and hence diverge even more from the model prediction. Also shown is the component of τsp that is supported by ploughing particles. The difference between τsp and the ploughing component of τsp is the shear stress supported by stationary particles accommodated by regelation. (d–f) Same parameters but for a model of the bed consisting of sinusoids with wavelengths equal to 2R and amplitudes equal to 0.2R.
Another possibility is that the water layer was thicker than 0.2 mm, and hence submerged more of the bed. Keeping in mind that the water-layer thickness is a parameterization for the extent of microcavity development in the lee of particles, a thicker water layer is not necessarily unreasonable. The shear stress that results from a water layer 10 mm thick is shown is Figure 7. Although τ sp is reduced significantly, the relation between P e and τ sp is linear, unlike that observed. The linearity results from the lack of regelation when all small roughness elements are drowned; shear stresses that are controlled exclusively by ploughing particles result in a linear relation (Equation (15)).
It has thus far been assumed that the mean thickness of the water layer between the ice and till is constant and independent of P e. A reasonable expectation, however, is that the extent of microcavity development, and hence the mean thickness of the layer, might increase as the water pressure approaches the ice-overburden pressure. Unfortunately, despite detailed studies of cavity hydraulics (Reference WalderWalder, 1986; Reference KambKamb, 1987), the relation between P e and cavity size, when P e is unsteady, is not well known. The approach taken here, therefore, was to seek a relation between P e and the water-layer thickness that provided a variation in shear stress that was in good agreement with the data and to then assess the plausibility of the relation.
The form of the relation should be such that the rate of increase in the thickness of the water layer increases as P e approaches zero. This results in disproportionately small values of τ sp at low ? e. An exponential increase in water-layer thickness as P e approaches zero, therefore, is a suitable choice.
The two possibilities illustrated in Figure 8a were applied to the bed consisting of hemispheres for the case of cavity formation. In the first case, in which the film thickens to 0.01 m at P e = 0, regelation limits the shear stress on some size classes only if ? e > 41 kPa (Fig. 8b). In the second case, in which the water layer thickens to 0.06 m at P e = 0, all particles in contact with ice plough over the full range of P e. Owing to the absence of regelation and the increase in ice/bed contact area as P e increases, the model results are in reasonable agreement with the observed relation between τ sp and P c (Fig. 8c).
As discussed in Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others (1999), the measured variation in P e was a good deal larger than the range inferred at the site of the tiltmeter, where the record of basal shear stress was obtained. This is likely because water pressure was measured in a subglacial channel rather than at the ice/till interface. Because parts of the bed were undergoing water-pressure fluctuations larger than those inferred at the site of the tiltmeter, the model results of Figure 8c were extended over the full range of P e detected beneath the glacier (Fig. 9). As P e increases, values of τ sp increase to a value greater than 200 kPa and then begin to decrease after P e is too large to allow ploughing of even the largest particles. This decrease in τ sp results from the reduction in sliding speed as P e increases. The ultimate strength of the till, obtained from ring-shear tests (Reference Fischer, Iverson, Hanson, Hooke and JanssonIverson and others, 1998), is less than τ sp over an intermediate range of effective stress, 80 kPa < P e < 320 kPa. Over this range, critical-state deformation of the bed should occur and will limit the basal shear stress. At smaller P e, ploughing limits the basal shear stress and there will not be critical-state deformation of the bed, although if the basal shear stress exceeds the yield strength of the till there may be transient deformation like that observed at the site of the tiltmeter. At larger P e, the ultimate strength of the till is too large to allow critical-state deformation, and the basal shear stress is limited by ploughing and the traditional sliding mechanisms.

Fig. 7. The calculated value of τsp (thick, solid line) and the component of τsp that is supported by ploughing particles (thin, solid line), assuming a reduced upper fractal limit of 0.01 m to simulate complete burial of the largest size fractions. Also shown is the calculated value of τsp if the water layer has a thickness of 10 mm (dotted line), rather than 0.2 mm as in Figure 6. In this case, all particles in contact with the ice are expected to plough.
Discussion
A key question is whether the variation in water-layer thickness required to bring the model result into agreement with the observed relation is plausible. More specifically, is an exponential increase in the areally averaged height of a system of linked microcavities at the ice/till interface probable, or even possible, as the basal water pressure approaches the ice-overburden pressure?
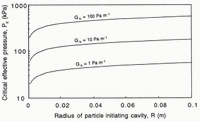
Analyses of the steady flow of water through linked cavities should provide some insight into this problem, deferring for the moment the complexity added by the un-steady water pressure beneath Storglaciären. That of Reference WalderWalder (1986) is the simplest and is in general agreement with the more complex analysis of Reference KambKamb (1987). Both studies found, in accord with the force balance of Reference IkenIken (1981), that below some critical effective pressure, P c, interconnected cavities will increase in size without bound because the creep closure rate is exceeded by the rate of cavity opening by sliding and wall melting. The variations in water-layer thickness with P c postulated here (Fig. 8a) would imply values of P c on the order of 100 kPa. If cavities in the lee of particles are idealized as step cavities with heights that are generally sufficient for turbulent flow, then the theory of Walder (1986, equation (13)) can be used to evaluate whether a value of P c of this magnitude is reasonable. He found that
where G h is the hydraulic gradient (Pa m-1) along the local flow direction within cavities and κ is a constant. Due to both the tortuosity of a linked-cavity network and the likelihood that most of the reduction in hydraulic potential will occur in small constrictions between cavities, rather than in the cavities themselves, values of G should be significantly smaller than would otherwise be anticipated. Walder suggests that the range, 1.0–100 Pa m-1, is reasonable. The value of κ depends on the cavity geometry, the material properties and flow law of ice, and the Manning roughness of cavities. Using the parameter values listed by Wälder to compute κ, Equation (19) then suggests that unbounded growth of cavities at effective pressures on the order of 100 kPa is plausible (Fig. 10).

Fig. 8. Assumed relations between the thickness of the water layer and effective pressure. (b) Fractional area of the bed occupied by ploughing particles and by stationary particles accommodated by regelation for the two cases shown in (a). For case 2, all particles in contact with ice are expected to plough. (c) The calculated value of τsp for the two cases shown in (a). Also shown for case 1 is the component of τsp that is supported by ploughing particles.

Fig. 9. Model results for case 2 of Figure 8 extended over the full range of Pe measured beneath Storglaciären. Deformation of the substrate in the critical state is expected only at effective pressures of 80–320 kPa, the range over which τsp exceeds the ultimate strength of the till. Otherwise, most motion should he focused near the glacier sole by sliding and ploughing.
Another important question is whether the magnitude of ice/bed separation needed to fit the data, up to 0.06 m at zero effective pressure, is unreasonably large. Sub-daily measurements of glacier surface uplift might help answer this question, but such data have not been gathered at Storglaciären. On Findelengletscher, Switzerland, where uplift has been measured at sub-daily intervals, increases in basal water pressure to values larger than the ice-overburden pressure have resulted in upward displacements that exceed 0.06 m over periods less than 1 day (Reference Iken and BindschadlerIken and Bindschadler, 1986). However, the fraction of the measured uplift that results from cavity opening is unclear. Water storage in the glacier provides an additional constraint on mean ice/bed separation. Estimated increases in water storage in Storglaciären during rainstorms (Reference CutlerCutler, 1996) usually exceed that required to fill cavities of the mean heights considered here. Thus, although a mean cavity height of several cm suggests extensive ice/bed separation in zones where ice is in contact with till, such thicknesses cannot he ruled out and may have occurred at least locally at the site of the tiltmeter where the record of shear stress was obtained.

Fig. 10. The critical effective pressure required for unbounded cavity growth as a function of the hydraulic gradient and the radius of the particle that initiates the cavity, as predicted by the theory of Reference WalderWalder (1986).
A related uncertainty is whether a system of interconnected microcavities should expand and contract over periods as short as one to several days, the time-scales over which water pressure fluctuated beneath Storglaciären (Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999, fig. 8). Numerical calculations of the transient response of channel geometry to pressure fluctuations suggest that, in general, channels cut into the glacier sole will not respond fully to water-pressure fluctuations over such time-scales (Reference CutlerCutler, 1996). However, the rate of response of linked cavities should be different from that of a Röthlisberger channel. A reduction in P e on a linked-cavity system will increase the cavity size at a rate proportional to the sliding speed. Reference KambKamb (1987) showed that if the reduction in P e is a large fraction of the total effective pressure, the rate of cavity growth should approximately equal the sliding speed. Instantaneous rates of cavity expansion might, therefore, approach 0.1 m d-1 beneath Storglaciären and could therefore account for rapid increases in the extent of ice/bed separation. The closure of cavities at similar rates is more problematic because the rate of closure is limited by the inward creep rate of ice. One possibility is that cavities that have grown rapidly in response to low P e may be sufficiently elongated once P e begins to increase that closure rates are much larger than those of a relatively equant void.
Although an exponential increase in water-layer thickness at the ice/bed interface does provide an explanation for the observed variation in the shear stress with P e, there are other possible explanations. For example, no attempt has been made here to account for the interference of stress fields between adjacent particles in the ice or till that could change the magnitude of shear stresses supported by individual particles. The extent of such interference might vary with P e, as the fractions of bed accommodated by the different flow mechanisms change. It is also possible that the agreement between the modeled and observed shear stress might be optimized by a particular distribution of grain-sizes at the bed surface, for example, a concentration of fine sediment. Although basal tills usually do not display such systematic sorting, a grain-size distribution at the bed surface radically different from that of the till as a whole cannot be ruled out.
Comparison of the calculated values of τ sp with the ultimate strength of the till indicates that the mode of basal motion at Slorglaciärcn may be quite sensitive to the effective pressure (Fig. 9). For values of P e less than 400 kPa, τ sp does not differ by more than about 30 kPa from the ullimale strength of the till, the stress required for steady till deformation. Thus, a variation in P e that causes a small change in τ sp may change the mode of basal motion. Although the uncertainty in this estimate of τ sp is probably large, the predicted sensitivity to P e is supported by temporal changes in the distribution of motion with depth in the bed associated with water-pressure fluctuations both at Storglaciären (Reference Hooke and IversonIverson and others, 1995; Reference Hooke, Hanson, Iverson, Jansson and FischerHooke and others, 1997) and at Trapridge Glacier, Yukon Territory, Canada (Reference Blake, Fischer and ClarkeBlake and others, 1994). Because P e varies spatially beneath glaciers, it is also apparent from Figure 9 that the partitioning between ploughing, bed deformation and the traditional sliding mechanisms may vary spatially beneath a single glacier. This is cause for caution in the interpretation of borehole studies, which provide only a limited view of the bed (e.g. Reference Blake, Fischer and ClarkeBlake and others, 1994; Iverson and others 1995; Reference Engelhardt and KambEngelhardt and Kamb, 1998).
A question of considerable cm-rent interest is whether the bed of Ice Stream B is deforming at depth, Reference Alley, Blankenship, Bentley and RooneyBlankenship and others (1987) inferred from the high porosity of the basal sediment that it was dilatant throughout its thickness and hence shearing. In contrast, Reference Engelhardt and KambEngelhardt and Kamb (1998), on the basis of one direct measurement of sliding beneath Ice Stream B, concluded that deformation of the bed was minimal at depths more than a few cm below the ice/bed interface.
Given the scant data on the mode of basal motion beneath Ice Stream B, it is of interest to use the present model to estimate the shear stress there due to sliding and ploughing for comparison with the ultimate strength of the basal sediment. Parameter values are reasonably well known. U is assumed to be equal to the surface speed of the ice stream. 1.2 m d -1 (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). The thickness of the water layer is taken to be 0.1 mm, the maximum value indicated by the borehole studies of Reference Engelhardt and KambEngelhardt and Kamb (1997). The ultimate friction angle of the sediment beneath Ice Stream B is about 24°, and cohesion is negligible (personal communication from S. Tulaczyk, 1997). The upper fractal limit of the grain-size distribution is assumed to be 1.0 m, in accordance with earlier analyses (Reference AlleyAlley, 1989), The fractal dimension of the grain-size distribution was calculated from weight fractions in each size class (Reference Tulaczyk, Kamb, Scherer and EngelhardtTulaczyk and others, 1998), yielding a value of 2.99. This is larger than the value calculated by Reference Hooke and IversonHooke and Iverson (1995) from data presented by Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others (1990). However, those data apparently did not include the finest fraction of the grain-size distribution (personal communication from S. Tulaczyk, 1996). Other parameters in the calculation were specified as before.
The calculated shear stress due to sliding and ploughing is about 60% less than the ultimate strength of the till (Fig. 11), suggesting that basal motion may well be focused at the glacier sole, rather than at depth In the bed. Although there may be considerable uncertainty in this calculation, the tendency of the model, without an adjusted water-layer thickness, is to overestimate, rather than underestimate, τ sp (Figs 6 and 7). Up to an effective pressure of 160 kPa, the largest effective pressure observed beneath Ice Stream B (Reference Engelhardt and KambEngelhardt and Kamb, 1997), τ sp is limited wholly by-ploughing. Ploughing limits τ sp because the high rate of basal motion results in potential driving stresses on particles that are too high to allow the traditional sliding mechanisms to operate without dragging particles through the bed.
The 0.1 mm thick waler layer assumed in this calculation is an order of magnitude thinner than the minimum considered reasonable by Reference Alley, Blankenship, Bentley and RooneyAlley and others (1987). If the water layer is, indeed, thicker than has been assumed here, values of τ sp would be smaller than those calculated, further increasing the likelihood that shear stresses on the bed would not be sufficient to deform it, except locally around ploughing particles. On the other hand, the water layer may be thinner than that assumed here. If the thickness of the water layer scales inversely with the effective pressure, then where the effective pressure is high, for example near the “canals” (Reference Walder and FowlerWalder and Fowler, 1994) postulated by Reference Engelhardt and KambEngelhardt and Kamb (1997), it is possible that the water layer is sufficiently thin to allow pervasive deformation the bed.
Ploughing should also be enhanced and pervasive deformation of the bed suppressed beneath Ice Stream B due to pore pressures in excess of hydrostatic down-glacier from ploughing particles. Although this effect is not easily incorporated into the calculation of τ sp, the minimum particle size required to generate excess pore pressure can be calculated from Equation (16). At Ice Stream B, the sediment permeability k p is 2 × 10-16 m2 (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). Given the clay-rich basal sediment, the compressibility, α, should be approximately 10-6 Pa-1. Over the range of P e relevant here, the particle speed, U p, should be only slightly less than the sliding sliced, so U p is approximately 1.2 m d-1 (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). Remembering that for r < 1.5 significant excess pore pressures are expected and that δ in Equation (16) is approximately equal to diameter of the ploughing panicle, the minimum particle diameter required to generate significant excess pore pressure is then 5.4 mm. Thus, down-glacier from ploughing particles larger than this, till is expected to be weaker than elsewhere. This effect, demonstrated in studies of cone penetration (Fig. 2), increases the likelihood that motion beneath Ice Stream B occurs near the glacier sole by ploughing.
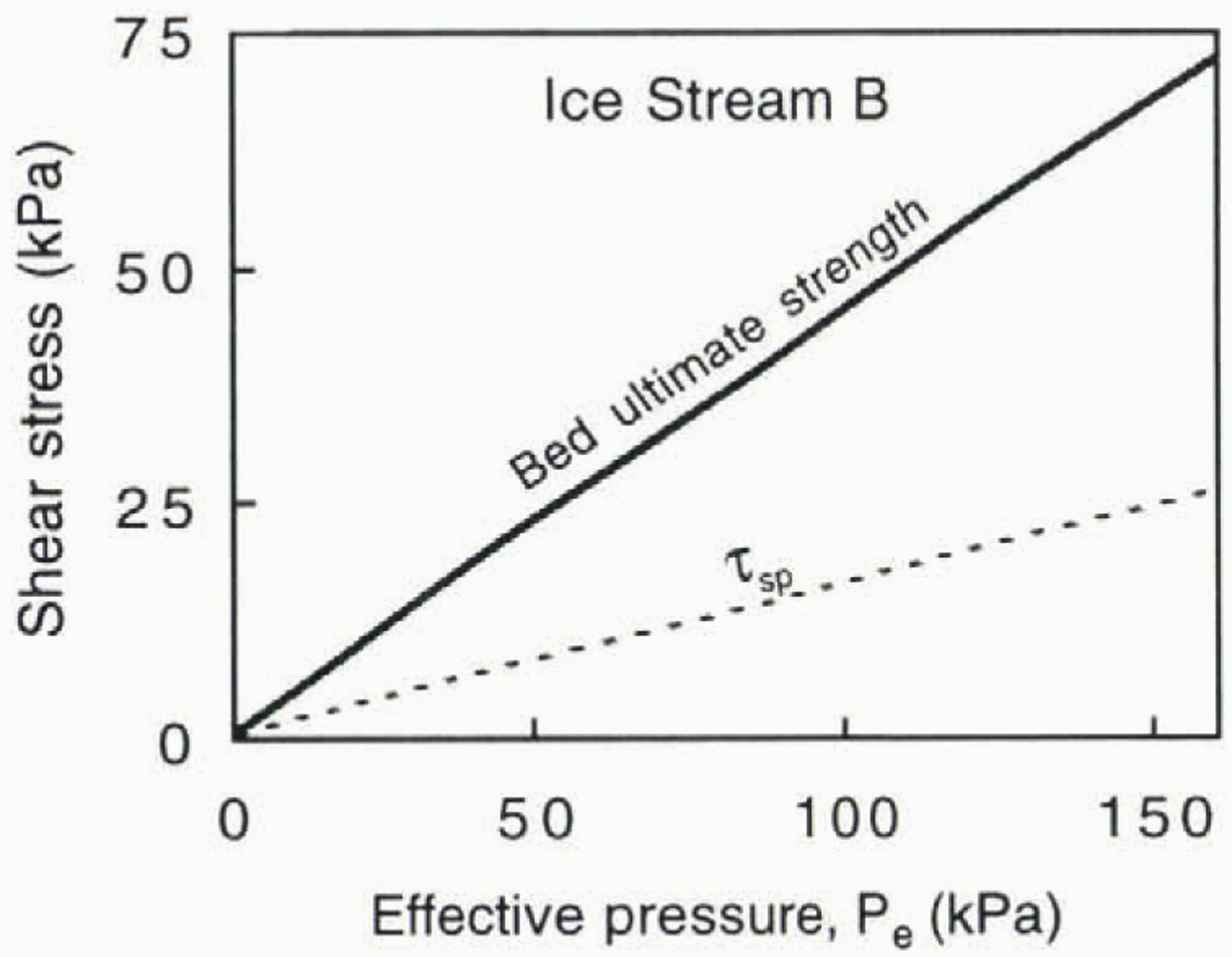
Fig. 11. The calculated value of τsp at Ice Stream B and the ultimate strength of the basal sediment there.
Conclusions
Sliding theory and a treatment of ploughing based on cone-penetration studies provide the basis for calculating the shear stress, τ sp, that ran he supported by sliding and ploughing beneath Storglaciären. At low effective pressures characteristic of glaciers on soft beds, τ sp is the sum of regelation-limited drag on small particles and ploughing-limited drag on larger particles. Ploughing is the dominant stress-limiting flow mechanism. Thus, τ sp increases with effective pressure, P e, due to strengthening of till down-glacier from ploughing particles.
Measurements of τ sp, based on the elastic deformation of till recorded by a tiltmeter beneath Storglaciären, indicate that τ sp increases with P e 1.7 (Reference Iverson, Baker, Hooke, Hanson and JanssonIverson and others, 1999). Regardless of whether particles at the bed surface are assumed to form hemispherical obstacles or more subdued sinusoidal undulations as a result of burial in the bed, the model tends to overestimate τ sp and is in poor agreement with the observed form of this relation.
However, the calculated and observed relations between τ sp and P e agree better if the mean thickness of the water layer between the ice and the till, presumably determined by the extent of microcavity development there, increases exponentially to several cm as P e approaches zero. Support for the unbounded growth of linked cavities at a sufficiently low P e comes from analyses of cavity hydraulics (Reference WalderWalder, 1986; Reference KambKamb, 1987). However, it is uncertain whether the degree of ice/bed separation required is reasonable and whether cavity growth and collapse tracks water-pressure fluctuations over observed time-scales as short as 1 day.
Extrapolating the model results to effective pressures larger than those inferred at the site of the tiltmeter and comparing them with the ultimate strength of the till suggests that there may be three general regimes of basal motion at Storglaciären. At sufficiently small P e, ice/bed separation submerges all but the largest particles in water, τ sp is less than the ultimate strength of the till, and ploughing should limit the basal shear stress. Motion, therefore, should be focused near the glacier sole by ploughing. At intermediate P e, τ sp is larger than the ultimate strength of the till, and the bed, therefore, should deform at depth, although deformation should be accompanied to some degree by ploughing and sliding. At still larger P e, the bed is sufficiently rigid to inhibit both ploughing and deformation of the bed, and thus, the traditional sliding mechanisms should limit the basal shear stress. Spatial and temporal variations in the partitioning of motion between these flow mechanisms, therefore, are expected beneath glaciers where P e is sufficiently variable.
Application of the model to Ice Stream B suggests that the basal shear stress there may be limited by ploughing, and thus, that basal motion may be focused near the glacier sole. Pore pressures in excess of hydrostatic generated in sediment down-glacier from large ploughing particles, an effect not considered in the model or in other analyses, should weaken the till adjacent to stich particles, further increasing the potential for ploughing and reducing the likelihood that the bed deforms pervasively. However, there may be such deformation locally if the water layer between the ice and sediment is sufficiently thin in zones of relatively high P e.
An important assumption of the deforming-bed model of glacier motion is that basal ice is coupled sufficiently to the bed to deform it pervasively at depth. This study and subglacial measurements elsewhere (e.g. Reference Fischer and ClarkeFischer and Clarke, 1997) suggest that this assumption is sometimes, if not often, incorrect. Studies that invoke a thick deforming bed as the key element in the dynamics and sediment-transport capability of past and present ice masses should be evaluated with this in mind.
Acknowledgements
I thank R. LeB. Hooke and J. S. Walder for helpful comments on an earlier version of the manuscript, and S. Tulaczyk for providing data on the sediment beneath Ice Stream B. Constructive comments by S. Tulaczyk, W. Harrison and G. K. C. Clarke improved the paper. This work was supported by U.S. National Science Foundation grants OPP-9224209 and OPP-9530814.
Appendix Criterion for Cavities and Justification for Equation (10)
Consider ice flow past an isolated hemisphere of radius R on a flat bed. Define P s and P 1 as the average differences between the ice-overburden pressure, P i, and the bed-parallel component of the normal stress that ice exerts on the stoss and ice sides of the hemisphere, respectively. If D is the bed-parallel drag force, balancing forces on the stoss and lee sides yields

D = πR 2 τ s, where τ s is the local shear stress, and for a bump without a cavity, P 1 = − P s. Substituting these equations into Equation (A1) indicates that
Assuming that water under pressure, P w, has access to the lee of the bump, Lliboutry assumed that a water-filled cavity will form when the water pressure exceeds the mean pressure on the lee of the hemisphere, or when P w > P i + P 1. Thus, remembering that the effective pressure P e is defined as P i – P w and noting Equation (A2), cavities are expected when τ s > P e (Reference LliboutryLliboutry, 1979, p. 81).
This is a more approximate criterion than that of Reference Iken and BindschadlerIken and Bindschadler (1986), who considered the case of a sinusoidal bed of wavelength λ and amplitude a. In that case, a cavity is expected to form when P w > P i – λτ s/aπ or when λτ s/aπ > P e. This criterion, which differs from the criterion for a hemisphere by the geometric factor, λ/απ, is based on the minimum, rather than on the spatially averaged, under-pressure on the lee of the sinusoid. The integration necessary to obtain a criterion that is fully analogous to that of Iken and Bindschadler (see Reference Fischer, Iverson, Hanson, Hooke and JanssonHooke, 1998, equation. 7.11) is not possible for the case of a hemisphere.
To roughly approximate the local shear stress, τ c, on a bump with a water-filled cavity in its lee, assume that the cavity covers the full leeward half of the hemisphere. The up-glacier pressure on the lee surface is then P w. If it is assumed also that the cavity does not influence the average overpressure on the stoss surface, P s, then from Equation (A1) the approximate drag force, D c, is given by

Substituting D c = πR 2 τ c and P s = τ s into this equation and remembering that P e = P i – P w yields Equation (10).