Introduction
In the Northern Hemisphere, observation of seasonal snow cover is essential to, for example, climate change monitoring, flood forecasting and avalanche warning systems (e.g. Reference Martinec and RangoMartinec and Rango, 1986; Reference BrownBrown, 2000; Reference MognardMognard, 2003; Reference ShaffreyShaffrey and others, 2009). Snow microstructure is important for physical modelling of snow evolution and remote-sensing algorithms. Grain size is a critical parameter in the analysis of snowpack development and metamorphism (Reference ColbeckColbeck, 1982). It is also used as a proxy of snow microstructure in many remote-sensing applications (Reference Tsang, Kong and ShinTsang and others, 1985; Reference Pulliainen, Grandell and HallikainenPulliainen and others, 1999).
Global mapping of snow cover is possible with optical and microwave satellite instruments (e.g. Reference Hall, Riggs, Salomonson, DiGirolamo and BayrHall and others, 2002). The extent of the snow-covered area can be observed by using visual and near-infrared wavelengths (e.g. Reference Hall, Riggs and SalomonsonHall and others, 1995; Reference Maurer, Rhoads, Dubayah and LettenmaierMaurer and others, 2003), and snow water equivalent (SWE) can be determined from passive microwave measurements (e.g. Reference Chang, Foster, Hall, Rango and HartlineChang and others, 1982; Reference Pulliainen and HallikainenPulliainen and Hallikainen, 2001). Radiative transfer models are used to simulate microwave radiation from experimental measurements, and model inversion can be applied in retrieval of snow parameters from microwave observations. Among other snow parameters, snow emission models use grain size (Reference Tsang, Kong and ShinTsang and others, 1985; Reference Pulliainen, Grandell and HallikainenPulliainen and others, 1999) or correlation length (Reference Tsang and KongTsang and Kong, 1981; Reference StogrynStogryn, 1986; Reference Wiesmann, Mätzler and WeiseWiesmann and others, 1998; Reference Wiesmann and MätzlerWiesmann and Mätzler, 1999) to describe the effect of snow microstructure on microwaves. The models are very sensitive to changes in the parameter describing the microstructure; thus its parameterization has a direct impact on the accuracy of the inverted SWE (e.g. Reference Grenfell and WarrenGrenfell and Warren, 1999; Reference Mätzler and WiesmannMätzler and Wiesmann, 1999; Reference Roy, Goïta, Royer, Walker and GoodisonRoy and others, 2004).
Natural snowpacks consist of morphologically different layers (Reference ColbeckColbeck, 1991); layers have typically distinct grain size, grain type, density, hardness and wetness. Several methods of defining the snow microstructure have been presented. The physical size of snow grains (E) is traditionally defined visually as the largest diameter (mm) of a typical particle (Reference ColbeckColbeck and others, 1990; Reference FierzFierz and others, 2009). However, an acknowledged problem concerning E is that it is difficult to define and measure with good repeatability in field conditions (e.g. Reference Domine, Salvatori, Legagneux, Salzano, Fily and CasacchiaDomine and others, 2006). Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others (2001) present a comparison of E estimations made by several experts; the difference in estimation of E varied between 0.25 and 1.25 mm. Estimations were closest when grains were at an early stage of metamorphosis, i.e. grains were quite small and round. Other measures of individual grains more descriptive of the microwave behavior have been proposed by, for example, Reference MätzlerMätzler (2002).
The optical grain size (D 0), on the other hand, is defined as the diameter of independent spheres that have the same optical hemispherical reflectance properties as the snow, and which are proportional to the volume–surface ratio of the grains (Reference Giddings and LaChapelleGiddings and LaChapelle, 1961; Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference Dozier, Davis and PerlaDozier and others, 1987; Reference Grenfell and WarrenGrenfell and Warren, 1999). Therefore, D 0 is not the same as E of a particle, with the exception of material consisting of perfect spheres (Reference Wiscombe and WarrenWiscombe and Warren, 1980). Theoretical correlation length, on the other hand, describes the distribution of scattered radiation, and is related to grain size, shape and volumetric distribution of snow grains (e.g. Reference Debye, Anderson and BrumbergerDebye and others, 1957; Reference JinJin, 1993). However, three-dimensional measurements of the correlation length are difficult.
The physical snow evolution model SNOWPACK (Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others, 2002a) can be used to simulate the evolution of different characteristics of snow. Simulation of E is not a simple process, because the physical processes are variable and the shapes of snow crystals are complex; therefore, several equations and semi-empirical parameterizations are needed. In the non-dendritic case, when grains are not branched, D 0 is dependent on E. Independent equations are applied for the dendritic branched grains.
D 0 can be derived from specific surface area (SSA) measurements. SSA is a geometrical characteristic of porous sintered materials such as snow, and is related to chemical, physical and electromagnetic properties of the medium (Reference Grenfell and WarrenGrenfell and Warren, 1999; Reference DomineDomine and others, 2008; Reference Matzl and SchneebeliMatzl and Schneebeli, 2010). SSA can be measured by stereology (e.g. Reference Matzl and SchneebeliMatzl and Schneebeli, 2010), X-ray computed microtomography (Reference FlinFlin and others, 2005; Reference Chen and BakerChen and Baker, 2010), the methane adsorption method (Reference Domine, Cabanes, Taillandier and LegagneuxDomine and others, 2001; Reference Legagneux, Cabanes and DomineLegagneux and others, 2002) and optical methods (Reference Matzl and SchneebeliMatzl and Schneebeli, 2006; Reference Painter, Molotch, Cassidy, Flanner and SteffenPainter and others, 2007; Reference Gallet, Domine, Zender and PicardGallet and others, 2009; Reference LangloisLanglois and others, 2010; Reference ArnaudArnaud and others, 2011). Reflectance, and therefore optically measured SSA, also depends on grain shape (Reference Picard, Arnaud, Domine and FilyPicard and others, 2009). In this study, SSA was measured with the optical reflectance method presented by Reference Gallet, Domine, Zender and PicardGallet and others (2009).
The aim of the presented research was to: (1) compare in situ measured values to those modelled using the SNOWPACK thermodynamic snow model and (2) investigate the source and magnitude of measurement errors related to these parameters.
Theory and Measurement Methods
Grain growth
The shape and size of ice particles (referred to as snow grains from now on) change throughout the winter. Growth of snow grains is caused by changes in ambient physical conditions (Reference Adams and BrownAdams and Brown, 1982; Reference ColbeckColbeck, 1982); the strongest effects are caused by changes in temperature and density.
Temperature differences in the snowpack are related to differences in air temperature, thermal conductivity of snow, terrain, vegetation, elevation and the amount of sunlight. Land-cover type affects the structure of the snowpack (e.g. an ice layer over a bog forms a different base for the snowpack than dry ground). Furthermore, even if the ambient temperature remains stable, the snowpack exhibits a vertical temperature gradient in conditions where the ambient and subnivean temperatures differ because of the low thermal conductivity of snow. Changes in snow density are also induced by temperature changes; however, the snowpack also compacts at constant temperatures, new snow increases the pressure in the older snow, and density of the snow increases.
Changes in temperature and density affect the state of grain metamorphism in the snowpack. Generally, metamorphism drives the formation of different grain shapes (Reference FierzFierz and others, 2009). Reference ColbeckColbeck (1982) describes grain shape changes through the winter; grains can form again several times, and a rule of thumb is that the average size of snow grains increases with age and depth of snowpack.
Snow class definitions
Snow grains can be classified by shape. In this paper, definitions following Reference FierzFierz and others (2009) are used: grain classifications include precipitation particles (PP), decomposing and fragmented precipitation particles (DF), rounded grains (RG), faceted crystals (FC), depth hoar (DH), melt forms (MF) and ice formations (IF).
Measurement site
Snow profiles were measured at the Arctic Research Centre of the Finnish Meteorological Institute (FMI), Sodankylä, northern Finland, (67.368°N, 26.633°E) over two snow seasons. Measurements were made between January 2012 and April 2013. The measurement site (IOA (intensive observation area)) was located in a clearing surrounded by a sparse pine forest (Fig. 1). The site hosted several automated measurements (e.g. snow temperature profile, soil temperature profile, soil moisture and SWE). The meteorological and radiation data used for modelling were measured at a distance of 500m from the IOA, where surroundings were similar to the IOA.

Fig. 1. (a) Aerial photograph of the Sodankylä facilities. IOA is the intensive operation area. Meteorological and radiation measurements, used to force the SNOWPACK model, were made 500m from IOA in a similar environment. (b) The measurement field covered with snow on a natural forest floor.
Snow cover at the site persists on average for 200 days, between the end of October and the end of May (Reference Pirinen, Simola, Aalto, Kaukoranta, Karlsson and RuuhelaPirinen and others, 2012). The thermal winter, when the daily average temperature falls below zero, typically begins near the end of September and ends near the end of May. The maximum amount of snow is, on average, 80 cm in March, followed by a snowmelt period lasting until May. For the two winter seasons (2012 and 2013) used in this research, the measured snow depth and temperature profiles are presented in Figure 2.

Fig. 2. Height of snow (upper, black curves) and temperature profile (difference of temperature at surface and base) of snowpack (lower, grey curves) during winters 2011/12 and 2012/13.
The seasonal snowpack in Sodankylä has large variations in grain size and density, and impurities from, for example, tree litter and inorganic soot. Vertical layering caused by weather effects is inherent in snowpacks; however, natural snow also exhibits a high degree of horizontal variability in layering and snow structure caused by wind, vegetation and terrain effects (Reference Sturm, Morris, Massom and JeffriesSturm and others, 1998). In the case of new snow, the surface of the snowpack is typically light, and new snowflakes are large and dendritic. For older snowpacks, densification typically increases towards the bottom layers. In the middle of the snowpack, snow grains are smaller and rounder than in the surface layers. Grain size further increases towards the ground; near the ground, snow consists of grains with a large range of different sizes. During winter, the thickness of the bottom layer (mostly DH crystals) increases, the proportion of small and large grains changes, and the proportion in the layer increases near ground. The structure of the snowpack varies annually, in particular as a function of the temperature gradient over the snowpack (between air and soil temperatures).
The most common grain shapes in Sodankylä are PP, DF, RG, FC, DH and MF. Occasionally over the winter, SH crystals occur. Melting and recrystallization of the surface snow during a warm period, followed by a cold period, creates a hard crust layer, which is classified as MFcr or sometimes as IF.
The average grain-size value for the whole snowpack was considered appropriate when analysing the time series of snowpack evolution. As snow pits are forcibly made at a different location each time, the dataset at hand encompassed both temporal and spatial variations in snow structure, which are difficult to separate from one another. A weighted average was calculated to alleviate the effects of spatial (horizontal) variability of grain size in the snowpack. As the propagation of electromagnetic radiation in snow is closely related to the SWE (depth × density), weighting with SWE gives a better proxy of the relative weight of the grain size in each layer in terms of microwave interactions, compared to simple depth-weighted averaging. Other methods include weighing the grain size of each layer by the assumed optical depth of respective overlying layers (e.g. Reference Tedesco and KimTedesco and Kim, 2006).
Snow-pit measurements
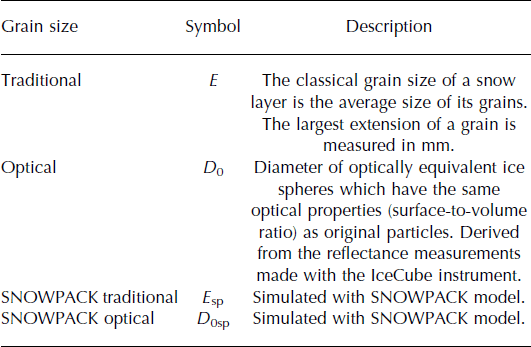
The research was based on manual snow-pit measurements made over the 2011/12 and 2012/13 winter seasons. The collected data include estimates of E as well as SSA measurements. SSA was measured with a commercial IceCube instrument (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). Grain-size measurements of E were performed by visually analysing macro-photographs of grain samples against a reference grid. Automated meteorological and radiation data from the test site were used to drive the SNOWPACK model; model estimates of E and D 0, given as E spi and D 0sp, aggregated over the snowpack to improve comparability, were analysed against the in situ measurements. The different grain-size parameters are presented in Table 1.
Table 1. Grain-size definitions
The collected dataset includes 35 snow-pit measurements, made over the two winters. Typically, the snow pits were measured at 1 week intervals. However, several extra measurements were arranged. Due to the destructive nature of the measuring process, the exact location of the snow pit changed each time; new pits were made at a minimum distance of 1 m from previous pits to avoid changes in snow structure caused by previous pit measurements. The data thus also include the effect of small-scale spatial variability, in addition to temporal variability caused by weather events and snow metamorphism.
All measurements from a snow pit were taken from a vertical cut of ∼50 cm width made in the snowpack. Layers were determined manually from the snow-pit wall by changes in snow structure (e.g. density, hardness, grain size and shape). The measured snow-pit data include snow layer thicknesses, E for each layer, temperature profile (every 10 cm), density profile measured by weighting a snow sample (every 5 cm), and SSA measurements (every 3 cm). However, reliable density and SSA measurements from 5–10 cm above ground level were not always possible due to hard packed or very coarse-grained snow.
E was estimated visually for each snow layer by comparing snow grains to a 1 mm reference grid. The methodology differed from the traditional measurement (Reference FierzFierz and others, 2009), because estimation was made during post-processing from macro-photographs. Occasionally, layers contained very hard snow and grains, and could not be distinguished without breaking the snow structure. Some of the photographs were also of low quality, so the grain-size estimation could not be made. Only one snow sample was taken from each layer, so errors in the definition of snow layers may have affected the representativity of the results. E was recorded to the nearest 0.25 mm. Photographs of different types of grains are presented in Figure 3. The snow type was determined visually from the same macro-photographs.

Fig. 3. Macro-photographs taken against a 1 mm reference grid in Sodankylä. Examples of dendritic (left) and non-dendritic (middle) grains. Grain shape in the left panel is PPsd, in the middle panel RGxf and in the right panel right FCxr. Grain size exhibits large variability in the right panel, likely causing observer-related bias. Grain size is more uniform in the other two photographs.
SSA measurements
A novel method of measuring D 0, the diameter of optical-equivalent ice spheres, is to derive it from measurements of reflectance (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). SSA (m2 kg−1) is defined as the surface area of particles per unit mass:
where S is surface area, M is mass of the sample, ρ i is the density of ice (917 kg m−2) and V is volume of the sample (Reference Legagneux, Cabanes and DomineLegagneux and others, 2002). The optical diameter of ice spheres is presented by Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004) as
The theoretical relation between D 0 and SSA from Eqns (1) and (2) is
The SSA decreases with increasing grain size, as there is more empty space between large grains than between smaller grains.
For SSA measurements, we used the IceCube manufactured by A2 Photonic Sensors, France, which is a commercial single-frequency instrument similar to DUFISSS (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). The instrument measures the hemispherical infrared reflectance of the snow samples, which can be linked to SSA (e.g. Reference Domine, Salvatori, Legagneux, Salzano, Fily and CasacchiaDomine and others, 2006; Reference Matzl and SchneebeliMatzl and Schneebeli, 2006). The whole snowpack was sampled at 3 cm intervals; the measurements were made from the same cut in the snowpack (i.e. pit) as the E estimations.
IceCube measurements consisted of calibration measurements and measurements of snow samples. The surface of the sample had to be smooth for the measurement to succeed; ice layers and very hard snow layers were difficult to measure, and several measurements were omitted as a result. Moreover, large crystals at the bottom of the snowpack proved difficult to sample correctly, so these measurements may carry additional errors. The sample also had to be compacted in the sample holder to avoid absorption of radiation at the bottom of the holder, which obscures reflections from the snow sample. For clustered grains (e.g. MFcl or MFpc), the SSA value was smaller, because grains were closer to each other than free grains of the same size would be (Reference Dozier and PainterDozier and Painter, 2004). During the measurement the sample holder was set below the instrument. Calibration measurements of the IceCube were made before and after every measurement occasion. The calibration result depended on, for example, the laser temperature, the cleanness of the spectralon surfaces and the mechanics of the instrument. The IceCube was calibrated by measuring the reflectances of six different spectralon plates and the background radiation. A least-squares polynomial was fitted to these seven measurements, and the success of the calibration was determined from the fit. The programme gives the user an estimate of the quality of the calibration from the success of the curve fit, by using a scale of very poor, poor, good and excellent. Error estimation of calibration is important, because the success of the calibration was not seen during measurement and some of the calibration measurements were often of poor quality. Errors may have originated from any single calibration measurement or multiple calibration measurements. Theoretically, it was also possible for all calibration measurements to be shifted systematically to the same direction to indicate good calibration, but the magnitude of the result (signal-toreflectance relationship) would then be erroneous.
Snowpack model
SNOWPACK is a one-dimensional (1-D) physically based finite-element model developed at the WSL Institute for Snow and Avalanche Research SLF, Switzerland. The characteristics of the numerical set-up, the microstructure and the initial and driving parameters of the model are described by Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others (2002a,Reference Lehning, Bartelt, Brown and Fierzb). The number of individual layers in the model is not restricted, and increases in response to snow precipitation.
SNOWPACK simulates three types of snow metamorphism: equilibrium metamorphism, temperature gradient metamorphism and wet snow metamorphism. Only the first two metamorphism simulations were investigated in this study.
The snow grains are parameterized using size parameters (grain size and bond size) and shape parameters (dendricity and sphericity). The sphericity describes the ratio of rounded versus faceted shapes, and the dendricity describes the part of original grain shapes that remain in a snow layer. Both parameters vary from 0 to 1. The dendricity and sphericity were set to 1 and 0.5, respectively, for new snow. In old rounded snow grains, the dendricity decreases to zero. The shape parameters are based on the French snow model Crocus. Further details can be found in, for example, Reference Brun, David, Sudul and BrunotBrun and others (1992).
Grain growth and thus grain size (E sp) is defined by several equations in the SNOWPACK model depending on the physical conditions in the snowpack. The grain growth during equilibrium metamorphism, as the temperature gradient is small, is based on a mixture theory model described by Reference Brown, Edens and BarberBrown and others (1999, Reference Brown, Satyawali, Lehning and Bartelt2001). E sp during equal temperature metamorphism is the diameter of a sphere. The grain growth rate (r g) is presented by Reference Lehning, Bartelt, Brown and FierzLehning and others (2002b) in the equal temperature metamorphism as

where T is temperature, t is time, s is sphericity, A 1, A 2 and A 3 are coefficients, r g is grain size, and T R is reference temperature (273.15 K). The temperature gradient metamorphism used in SNOWPACK is described by Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others (2001). It assumes that snow grains grow as plates, while the thickness of the plate stays constant. The length of a side of these plates is the temperature gradient metamorphism grain size in SNOWPACK. The grain growth rate is presented by Reference Lehning, Bartelt, Brown and FierzLehning and others (2002b) in the temperature gradient metamorphism as

where r g(0) is initial grain size, ρ i is density of pure ice, f gg is the adjustable geometrical factor for better approximation of the real grain shape (Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others, 2001; Reference Lehning, Bartelt, Brown and FierzLehning and others, 2002b), J L is interlayer mass, J L2L is layer-to-layer mass, r g(t) is actual growing grain size, a is lattice constant and z is snow height. Grain-size simulation of SNOWPACK has been fitted to grain-size measurements by adjusting model parameters empirically with cold laboratory experiments.
The optical grain size (D 0sp), which is simulated with SNOWPACK, is presented in Reference VionnetVionnet and others (2012) in the dendritic case as
and in the non-dendritic case as

where D 0sp (m) is the SNOWPACK optical grain size, d is dendricity, s is sphericity and E sp (m) is SNOWPACK traditional grain size. Thus the D 0sp in the non-dendritic grains depends on E sp.
In this study, version 3.1.0 of SNOWPACK was used to simulate E sp and D 0sp for winters 2011/12 and 2012/13. Air temperature, relative humidity, wind speed and direction, incoming and outgoing shortwave radiation and snow depth observations were collected from an operational weather station (WMO code 02836) operated by the FMI at the Sodankylä Arctic Research Centre. These observations were augmented with automatic ground temperature observations and snow temperature observations close to the operational station. Incoming and outgoing longwave radiation observations were available, but the longwave radiation data contained gaps preventing their application in simulations. Therefore, only shortwave radiation data were used. In simulations for this study, SNOWPACK was driven by snow depth observations instead of precipitation data. Density of new snow was determined following Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others (2002a). The data used to drive the model have 30 min intervals, and the data used for the simulations are listed in Table 2 and in the Appendix. The SNOWPACK model outputs the parameters of snow profiles at 60 min intervals.
Table 2. Summary of automated measurements used to drive the SNOWPACK model

SNOWPACK grain size has been compared to measured grain size and grain type in several recent studies (Reference Schweizer, Bellaire, Fierz, Lehning and PielmeierSchweizer and others, 2006; Reference Rasmus, Gronholm, Lehning, Rasmus and KulmalaRasmus and others, 2007; Reference Hirashima, Nishimura, Yamaguchi, Sato and LehningHirashima and others, 2008). Reference Rasmus, Gronholm, Lehning, Rasmus and KulmalaRasmus and others (2007) calculated agreement scores for measured and simulated grain sizes in Finland; agreement was generally good in northern Finland, where the snowpack was more stable. On the other hand, Reference Schweizer, Bellaire, Fierz, Lehning and PielmeierSchweizer and others (2006) compared measured and simulated grain size for each grain type, finding no large differences between measured and simulated grain sizes. Reference Langlois, Royer, Derksen, Montpetit, Dupont and GoïtaLanglois and others (2012) compared the correlation length derived from D 0 measured by InfraRed Integrating Sphere (Reference MontpetitMontpetit and others, 2012) and SNOWPACK model results, and scaled D 0 lower to fit measurements to simulations. Reference Huang, Margulis, Durand and MusselmanHuang and others (2012) researched grain sizes predicted by different models. Their result was that SNOWPACK predictions for E and D 0 are as good as predicted by using two other models (Flanner–Zender Grain Size Model (Reference Flanner and ZenderFlanner and Zender, 2006) and Jordan Grain Size Model (Reference Sun, Jin and XueSun and others, 1999)) which both predict the size parameters well.
Results
Comparison of experimental and snowpack modelled grain sizes
Time series of E, D0 and density profiles in Sodankylä snowpack
Profiles of E and D 0 are presented in Figure 4 for a single snow pit in February. The layered structure of the snowpack was visible in both the E and D 0 profiles. Generally, the magnitude of E was larger than the magnitude of D 0. Nevertheless, both measures indicated a similar trend of increasing grain size towards the bottom snow layers. Both methods indicated relatively small variation in grain size above a snow height of 20 cm. However, in lower layers the grain-size variability increased significantly.

Fig. 4. E (crosses) and D 0 (dots) compared using measurements made at 3 cm intervals for a single snow pit.
Density, E sp and D 0sp were modelled with SNOWPACK from meteorological and radiation data as described above and in Table 2 and the Appendix. Manual density measurements are compared to SNOWPACK simulations in Figure 5.

Fig. 5. Snow density simulated with SNOWPACK compared to manual density measurements. Coloured boxes represent manually measured values; solid lines represent SNOWPACK simulations: (a) 2011/12; (b) 2012/13.
The bias in snow thickness between manually measured and automatic observations, used as forcing for SNOWPACK simulations, was ∼5 cm during the dry snow season (Fig. 5). Both measured and simulated density values exhibit an increasing trend from snow surface towards the ground, from 50–150 to 300–500 g cm−3 in simulated and 50–200 to 250–450 g cm−3 for typical measured values in top and bottom layers, respectively. During the dry snow season, average densities for the 2011/12 winter were 208 and 175 g cm−3 and for the 2012/13 winter were 187 and 217 g cm−3 for measurements and simulations, respectively. During the melt season, density increased by up to 50% in both simulated and measured values. Some differences were apparent between two winter seasons: For instance, during the 2011/12 winter, density was notably large during the melt season, with measured values reaching 470 g cm−3. However, for the 2012/13 winter, the maximum measured densities during the melt season were 400 g cm−3, although the density in bottom layers was larger during the dry-snow season than for the 2011/12 season.
Time series of E, E sp, D 0 and D 0sp profiles are presented in Figures 6 and 7. The range of values for E was 0.25–2.75, for E sp was 0–2.5, for D 0 was 0–1.25 mm and for D 0sp was 0–1.5 mm. Typically, grain growth towards the bottom of the snowpack was apparent both in SNOWPACK simulations and measured data. The simulated layering profile can be compared to manually determined layering structure based on Figure 6; the measured E for manually determined layers is marked on the upper edge of the respective layer. Typically, SNOWPACK simulated more layers (up to >40) than could be determined by the snow-pit observation (typically not more than ten layers). In order to allow intercomparison of E, E sp, D 0 and D 0sp in a consistent fashion, E sp and D 0sp were weighted with the SWE of each layer. A similar method was applied for in situ data. This was seen as a necessary process due to ambiguities in relating the many simulated layers to the relatively few layers apparent in manual observations. Furthermore, as described earlier, snow-pit observations do not represent temporal evolution of a discrete location but also contain the effect of spatial variability in the natural snowpack.

Fig. 6. SNOWPACK simulation of E sp compared to manual measurements of E. Coloured boxes represent manually measured values; solid lines represent SNOWPACK simulations: (a) 2011/12; (b) 2012/13.

Fig. 7. SNOWPACK simulation of D 0sp compared to manual measurements of D 0 for snow pit 14 February 2013. Coloured boxes represent manually measured values; solid lines represent SNOWPACK simulations: (a) 2011/12; (b) 2012/13,
Averaged time series of E and D0 in Sodankylä snowpack
The time series of both manually measured and simulated E and D 0 are presented in Figure 8. Root-mean-square (rms) errors, unbiased rms errors, biases and correlation coefficients (R 2) of datasets are presented in Table 3. For the time series of E and E sp in winter 2011/12, R 2 was 0.56 and the bias 0.12 mm. For winter 2012/13 the variations were larger (with a bias of 0.26 mm) and the R 2 was 0.36. R 2 during January–March was 0.91 and 0.28 during the first and second winters, respectively. R 2 was 0.14 and 0.54 in October–December, and 0.20 and 0.32 in the melt season of the same two seasons respectively.

Fig. 8. Time series of measured E and D 0 and SNOWPACK simulated E sp and D 0sp. (a) 2011/12; (b) 2012/13.
Table 3. Correlation coefficient (R2 ), bias, rms error and unbiased rms error between measured and SNOWPACK simulated grain sizes. Grain sizes are defined in Table 1

D 0sp and D 0 trends were similar for both winters, and R 2 for the whole season was 0.75 for both seasons. During January–March 2012, R 2 was 0.42, and during January–March 2013, 0.76. R 2 was 0.27 and 0.94 respectively in the melting seasons and 0.79 in October–December 2012. However, D 0sp was constantly larger than D 0. Therefore, the bias and rms error between D 0 and D 0sp were larger than between E and E sp.
A linear scaling factor β sp describing the ratio between measured and simulated grain size can be defined so that
where D is measured grain size and D sp is simulated grain size. Values for β sp and standard deviations are presented in Table 4 and Figure 9 for the two snow seasons. Average scaling factors between the two years were within 0.1 of each other on average. Considering both winters, the scaling factor, βD 0sp, between measured D 0 and simulated D 0sp was 2.1, and βE sp between measured E and simulated E sp was 1.2. The standard deviations were 0.42 and 0.36 respectively. βE sp varied between 0.8 and 2.1 over both winters. βE sp was more stable during the first winter than the second, with values in the range 0.9–2.3 compared to 0.8–1.8 for the first and second winters, respectively. βE sp was largest during October–December and the late melting season, reaching values up to 2.3. In January–March, βE sp was 1.1 on average. Also βD 0sp was more variable during the second winter (range 1.3–3.2) than the first (range 1.8–2.8). For βD 0sp, there was no clear seasonally related trend, but measurements in December 2012 required the largest βD 0sp (average 3.1) while measurements in the 2013 melting season required the smallest βD 0sp (average 1.75). In January–March, βD 0sp was ∼2.2. It can also be noticed that trends of βD 0sp and βE sp were similar during the second winter.
Table 4. The scaling factor beta between measured and SNOWPACK simulaled grain sizes. βE sp is for traditional grain size E, and βD 0sp is for optical grain size D 0. Standard deviations (std) are also presented


Fig. 9. Time series of scaling factors βE sp and βD 0sp between measured E and D 0 and SNOWPACK simulated E sp and D 0sp: (a) 2011/12; (b) 2012/13.
Sources of measurement errors
Several factors contribute to the uncertainty of estimates of E, including random errors arising from preparation of the snow sample, and systematic errors arising from the estimation process itself. Errors are mainly caused by layer definition in the field, placing grains in the reference plate from the snowpack, unsuccessful photographing, failure to distinguish the single grains in the macro-photograph, failure to measure the size of a grain using a 1 mm reference scale or choosing the typical average grain in the macro-photograph. Other contributions to the error may be made by (1) the snow structure being disturbed when a sample of grains is placed on the reference plate, and (2) separation of the grain boundaries in the macro-photographs not always being clear.
Determining the layered stratification of the snowpack was an important aspect of the snow-pit measurement, because E may vary both horizontally and vertically. However, the process was also subject to observer error. The method applied for manual layer definition has been described above. Separation of layers was occasionally difficult because differences between the layers were not always clear. An alternative instrument for the definition of snow layer boundaries is the Snow Micro Penetrometer (SMP) (Reference Pielmeier and SchneebeliPielmeier and Schneebeli, 2003), which may allow more objective separation of the layering structure.
An example of comparison for E estimations made by three observers from the same photographs is determined in Figure 10. Estimation of E was made from samples taken at intervals of 3 cm, in order to acquire more samples for comparison, and on the other hand, in order to compare with D 0 from the same snow sample. The snow pit chosen for comparison included several layers and snow types. The difference between estimations was largest at the bottom of the snowpack, where the sample contained a large scale of different grain sizes (Fig. 3). Even if all the grains in the photograph were almost the same size, there was a potential error of up to 0.25 mm (the precision of our estimation). More comparative data are needed for a more complete error analysis of E.

Fig. 10. An example of observer-related errors in E estimations. The macro-photographs taken by 3 cm intervals were analysed separately by three observers; the mean value of E (crosses) is marked with error bars between minimum and maximum values.
The errors in the IceCube measurement were a sum of random errors originating from the sampling process as well as systematic errors in instrument calibration. Preparation of the samples for the IceCube instrument involved several uncertainties caused by the compaction level of the snow in the sample holder (reflection from the bottom of the sample holder) and the sample surface smoothness (reflection from the sample surface). The errors in instrument calibration were caused by the cleanness of calibration spectralons (shade of the spectralons) and the descent temperature of the instrument and laser (power of the laser). Additional errors were caused by instrument properties. For example, scattering from grains below the sample surface resulted in underestimation of the reflectance, which appeared to be reduced by the limited field of view (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). Moreover, the radiation penetration depth depends on snow density, which was usually ∼1 cm; however, radiation did not penetrate the calibration spectralon plates as porous snow, which increased the amount of reflected radiation and worsened the accuracy of the calibration.
A total of 27 measurements included IceCube calibration data before and after the measurement. The average difference in D 0 between two calibrations was 0.044 mm. The reflectance data of the largest and smallest differences between calibrations were used to derive D 0 in Figure 11. The largest difference (average from pit) was 0.113 mm on 10 April 2012, and the smallest average difference (average from pit) was 0.001 mm on 12 March 2013. Root-meansquare errors between these calibrations were 0.121 mm and 0.0025 mm respectively. Contrary to expectation, the largest differences in D 0 were between very poor and good calibrations, and the smallest were between good and poor calibrations, when the above scale is used. The average difference between D 0 of two calibrations made on the same day was still <0.05 mm
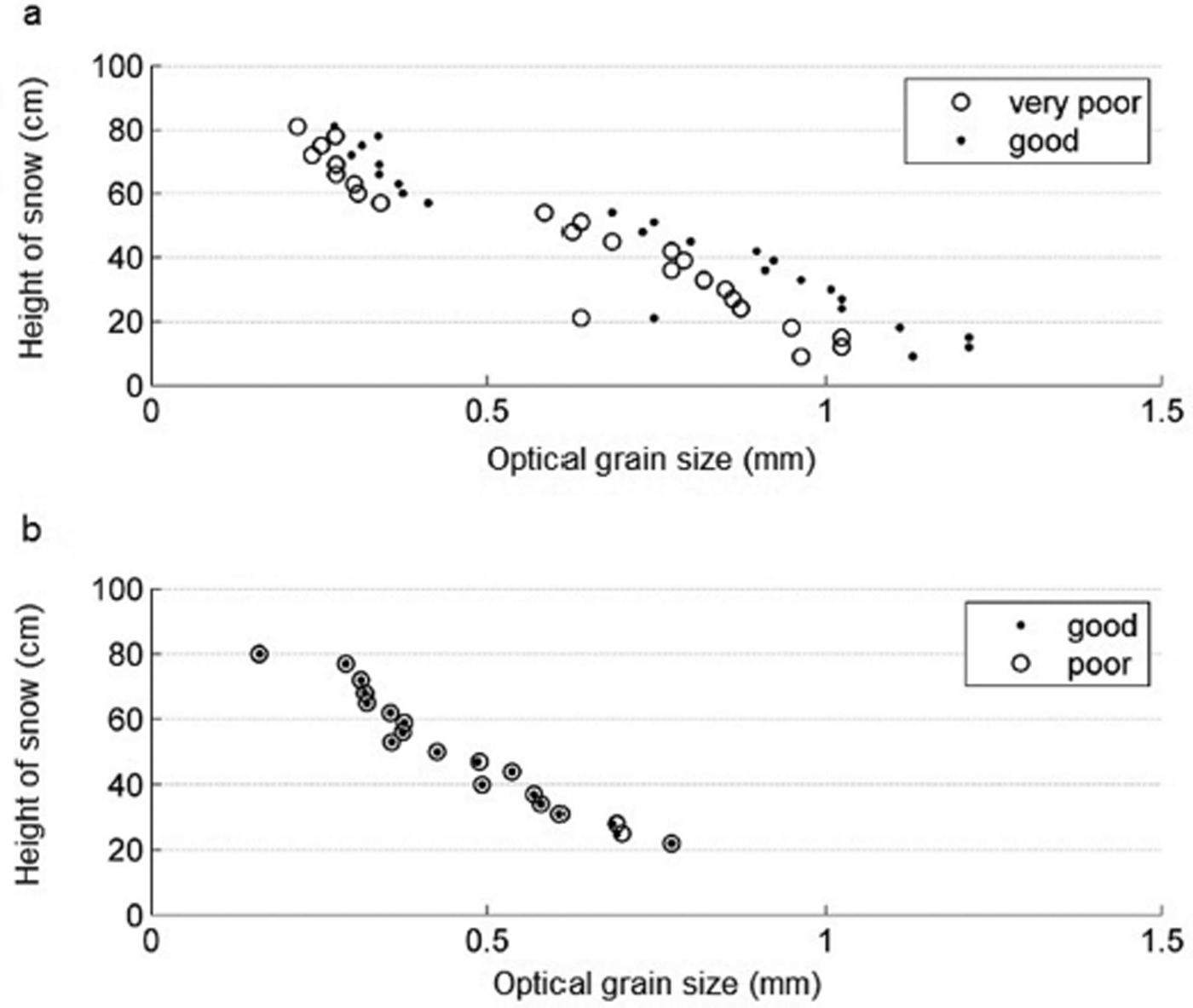
Fig. 11. The effect of repeated calibration of the SSA measurements on D 0. The same IceCube measurement is calibrated twice. On 10 April 2012, the mean difference between very poor (unfilled circles) and good (dots) calibrations of D 0 was 0.113 mm; on 12 March 2013 the difference between good (dots) and poor (unfilled circles) calibrations of D 0 was 0.001 mm.
Discussion
The magnitude of E was clearly larger than D 0 in both the measured and simulated cases. However, the magnitude difference between E sp and D 0sp was not as large as between E and D 0. Underestimation of D 0 may result partly from a lack of measurements from the bottom of the snowpack. Previous results also scaled D 0sp lower than in this study (Reference Langlois, Royer, Derksen, Montpetit, Dupont and GoïtaLanglois and others, 2012). The best correlation (from R 2, bias rms error and unbiased rms error) was between D 0 and D 0sp and then E and E sp. The average scaling factor βE sp varied 13% from one winter to another, and βD 0sp was within 11%. Standard deviations of yearly scaling factors were in the range 0.3–0.5.
According to our results, SNOWPACK simulations of E sp and D 0sp showed the best agreement with field measurements during January–March conditions. For early winter in November and the snowmelt season in April and May, E sp and D 0sp varied most, and a clear disconnect from field measurements was also apparent. During October–December, only a few snow layers were identified in field measurements; thus the variability in individual observations of E and D 0 affected the overall bulk average and the calculated average scaling factor. Overestimation of SNOWPACK density also affected the weak correlation of E and D 0 measurements with simulations during the melt season. Furthermore, measurements of E and D 0 also exhibit more uncertainties during the melt season in wet snow conditions.
Determination of layers, placing the grains in the reference plate and observer-related estimation causes the largest errors in E. Choosing the average E from the macro-photograph is the most sensitive part for error estimation. A comparison of estimates from three observers of the same macro-photographs indicated errors up to 1 mm. D 0, measured using the IceCube instrument, however, was less sensitive to observer- related errors than E estimates, but several stages of the measurement process (sampling, calibration of original values, deriving D 0 from SSA) may still result in inaccuracies. The light newly fallen snow (density ∼50 g L−1) had to be compacted in the sample holder, and the quality of the sample was affected by different sampling techniques, smoothness of the sample surface, etc. The calibration-related error was relatively small (average 0.05 mm; maximum 0.12 mm). Error is very small because calibrations are made during the same measurement occasion. Calibration errors were further reduced by cleaning calibration spectralons, and stabilizing the instrument and laser temperatures before the calibration.
Conclusions
A description of the snow microstructure is essential for physical snow models and radiative transfer models. A typical measure applied as a proxy indicator of snow microstructure has been the grain size (E). However, there are several ambiguities related to defining and measuring E. An alternative parameter describing snow microstructure, the optical grain size (D 0), can be derived from SSA measurements (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). However, the definition of D 0 is based on optics, and its measurement is based on optical reflection from snow, which is not directly related, for example, to the scattering behaviour of radiation at microwave frequencies. On the other hand, empirical relations between E and the propagation of microwaves have been established in the past (Reference Hallikainen, Ulaby and Van DeventerHallikainen and others, 1987). Physical snow models such as SNOWPACK are important for global derivation of snow properties that are difficult to observe in the field (e.g. grain size), for remote-sensing applications and hazard prediction systems. Therefore, a good correlation of manual measurements with the model is essential.
The main objective of the study was to compare E and D 0 to E sp and D 0sp. Another objective was to define measurement errors of E and D 0. The measurements were made during the 2011/12 and 2012/13 winters in Sodankylä.
Layers simulated with SNOWPACK were not directly comparable with the manually determined layering structure, as simulation typically produced more layers with also a differing density profile. Furthermore, collected field data also exhibited the effects of spatial variability in natural snow. Therefore, averaged and weighted values for the whole snowpack were used in this study for intercomparison of measured and simulated values.
The temporal variation of measured and simulated values was similar in the time series (Fig. 8); however, in the first winter the average correlation was better. The largest difference between measured and simulated values occurred in October–December and during the melting season in April and May. The magnitude of D 0sp was approximately twice as large as D 0, while the magnitude of E was almost the same for measured and simulated values (Table 3; Fig. 9). Calculated R2 values were best between the same respective measured and simulated parameters, even though the magnitude of D 0sp was closer to E than D 0 (Table 4).
The largest uncertainties in both E estimations and D 0 measurements were estimated to occur in the bottom layer of the snowpack, where the grains were large and loose. The IceCube calibration error was 0.05 mm on average. The effect of other errors (sampling method, sample surface smoothness and observer) on D 0 was <0.1 mm in our preliminary unpublished results. E for an average grain was estimated to the nearest 0.25 mm. The magnitude of error in E was suspected to be in the millimetre range (Fig. 11).
This study suggests that SNOWPACK was able to simulate with reasonable accuracy the magnitude and trend of traditional grain-size profiles for boreal forest/taiga snow in midwinter. In the case of optical grain size, SNOWPACK simulations exhibited a notably large bias compared to measured values; however, the correlation between measured and simulated values exceeded that of the classical grain size.
Acknowledgements
We thank the WSL Institute for Snow and Avalanche Research SLF and especially Mathias Bavay and Martin Schneebeli for the opportunity to use the SNOWPACK model. We also thank the staff of FMI Arctic Research Centre in Sodankylä for performing the in situ measurements.
Appendix
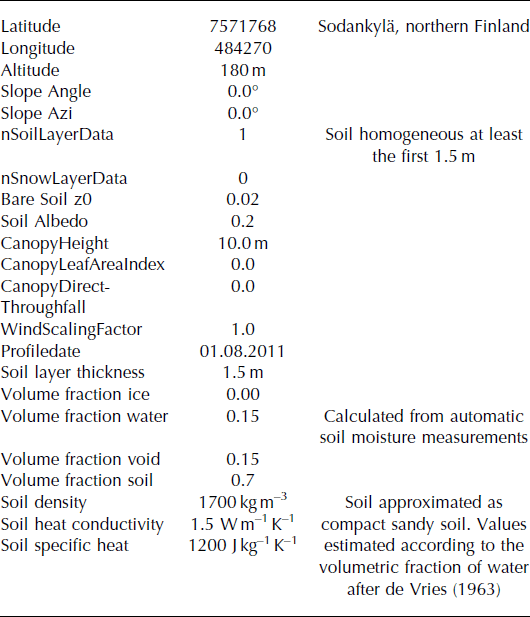
Table 5. SNOWPACK.ini file parameters

Table 6. SNOWPACK.sno file parameters