2.1. Ushkovsky volcano

The summit of Ushkovsky volcano (56°04′ N, 160°28′ E; 3903 m a.s.l.) forms a caldera 4 km in diameter that is completely covered with a glacier 43 km² in area. Two craters, Gorshkov and Herz, lie beneath the glacier at the highest part of the volcano (Fig. 1). The volcano is active, but there are no reliable data on its volcanic activity, and only minor fumarolic activity is currently observed (Reference Flerov, Ovsyannikov, Fedotov and MasurenkovFlerov and Ovsyannikov, 1991).

Fig. 1. Ushkovsky volcano (3903 m a.s.l.) and the summit craters.

The volcano is still active in the sense that regions on the crater rims are free from ice due to melting of the glacier by intensive geothermal heating. At such locations, subsurface temperatures sometimes reach 70°C. Intensive melting by geothermal heating is also observed in ice caves that are identified by holes in the glacier surface at Gorshkov crater (Fig. 2). By entering these holes, we found that the ice caves developed along the proximal slope of the crater rim and stretched for several hundred meters in both directions. The ice caves are also traced in the plan view photograph as elongated depressions along the crater rim (Fig. 2).

Fig. 2. A plan view of the summit craters, Gorshkov and Herz, and the distribution of annual mass balance (m) for 1997/98. Arrows denote a principal flow direction indicated by the surface gradient. Subsurface caves starting from an ice cave at the southwest rim are clearly indicated by depressions along the west to northwestern rim of the Gorshkov crater.

Reference Murav’yev and SalamatinMurav’yev and Salamatin (1989) estimated the horizontal and vertical velocities of the glacier at the cave as 0.20–0.33 and 0.33 ma⁻¹ ice equivalent, respectively. Reference Murav’yev and SalamatinMurav’yev and Salamatin (1989) and Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others (2000) concluded that the entire glacier might be melting at its base due to intensive geothermal heating as high as 10 W m⁻² (Reference Murav’yev and SalamatinMurav’yev and Salamatin, 1989) and 1.0–1.8 Wm⁻² (Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000). Introduction of such high geothermal heat fluxes resulted in estimation of younger ages of the glacier bottom in their mathematical depth-age calculations (∼650 years; Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000).

2.2. Geometry of the glacier filling the Gorshkov crater

Surface and bed topographies of the glacier filling the Gorshkov crater were determined by a topographic survey conducted in 1997 with a hand-held global positioning system, a theodolite and an impulse radio-echo sounding system (Reference MatsuokaMatsuoka and others, 1997, Reference Matsuoka and Naruse1999; Reference Shiraiwa and NaruseShiraiwa and others, 1999a). A total of 18 points denoted by solid dots in Figure 2 were fixed with triangulation to determine a principal flow direction of the glacier according to its surface topography.

The diameter of the submerged crater is approximately 800 m and the rim is exposed only at the southeastern edge to form the highest summit of Ushkovsky volcano (3903 m). The surface inclination of the glacier downward to the north was measured as 2° along the survey line R5–K4. We did not find any appreciable inclination along the survey transect from W4–E4. The principal flowline, therefore, is from an ice dome at the southern edge of the crater along a direction somewhat east of K4 as shown by an arrow in Figure 2.

Figure 3 shows a cross-section along the survey transect R5–K4 of the glacier that fills the Gorshkov crater. This crater is a slightly north-shifted concave bowl with a maximum measured ice thickness of 240 m at K2. It can also be seen from this cross-section, in conjunction with the plan view (Fig. 2), that the ice flows beyond the crater rim into the caldera at the northern end of the crater. This spillover implies that the glacier is not confined to the crater.

Fig. 3. Cross-section of the glacier filling Gorshkov crater. Marginal subsurface caves are depicted schematically. A series of dotted layers crossing the ice core at K2 are the basal accreted ice layers that appeared below 154 m. Two solid columns indicate the boreholes drilled in 1996 (BH1) and 1998 (K2).

2.3. Mass balance

To measure the mass balance at the surface, a series of snow stakes were installed at the glacier on 2 August 1996. Such mass-balance measurements were repeated during 10–18 June 1997 and also on 19 June 1998. The water-equivalent balances (in meters) at each point are shown in Figure 2 for the period 18 June 1997 to 19 June 1998.

In the balance year 1996/97, the mass balances were measured at three points: 0.38 m at BH1, 0.38 m at E4 and 0. 54 m at W4. During 1997/98, mass balances were obtained at 15 points. The values range from 0.19 m at E4 to 0.61 m at K3, with an average value of 0.42 ± 0.14 m. The mass balance tends to be higher in the central part of the glacier and lower in the western part. The lowest value recorded at E4 is due to its location, which is a wind-blown saddle. Although we have no information about the winter mass balance for this glacier, it is probable that wind scouring occurs near the western part of the crater. Redistribution of the snow in the central part of the crater is likely to be small because clear seasonal variations in oxygen and hydrogen isotopes were found in the ice cores.

The mass balance recorded in the balance year 1997/98 at K2, the drilling site, was 0.57 m a⁻¹ w.e. This is comparable with the average accumulation rate of 0.57 m a⁻¹ w.e. that was reconstructed for the last 27 years from a shallow ice core recovered in 1996 at BH1 (Reference Shiraiwa, Murav’yev and YamaguchiShiraiwa and others, 1997).

2.4. Surface snow temperatures

Snow temperatures were continuously measured at BH1 for 1 year using a 27 m borehole drilled in August 1996. Platinum resistance thermometers with an accuracy of ±0.1°C were installed at depths of 1, 2, 4, 5, 8, 10 and 27 m on 2 August 1996 for automatic measurements every 3 hours. They were collected a year later when the snow surface had increased by 0.79 m in height from that on 2 August 1996. Because the measurements were done without any maintenance, no correction was made for the depths of sensors according to the changing level of the surface.

Figure 4 shows monthly and annual mean temperature profiles at BH1 during 1996/97. Shallow parts of the profiles fluctuated with the seasonal cycles, but there were no indications of persistent melting temperatures at the surface. The annual average temperature at 1 m depth (1.79 m depth at the end of the observation period) was −16.6°C. The amplitude of the fluctuations decreases with depth. At 10 m depth, the average temperature was −15.8°C and the average amplitude was 1.3°C. The seasonal fluctuation becomes 0 at 27 m depth, where the snow temperature was constant at −14.6°C throughout the year. In later discussions, the annual average temperature profile given in Figure 4 is called profile BH1 (1996/97) average.

Fig. 4. Monthly and annual average snow-temperature profiles measured at BH1 (Gorshkov crater) from August 1996 to July 1997.

4.1. Stratigraphic features

Two distinct types of layering were observed in the firn and ice cores: firn layers that have not been affected by melting, and ice layers formed by melting and subsequent refreezing in the surface snow. The melt type was easily identified, with the aid of transmitted light, as clear layers devoid of bubble inclusions, even below the pore close-off depth. The nonmelting type was identified as layers including variable numbers of uniformly distributed bubbles (Fig. 5). The two types of layering are interbedded and of varying thickness.

Fig. 5. Ice-core sections showing two representative layers: firn layers that have not been affected by melting (whitish parts) and melt features formed by melting and subsequent freezing (clear parts indicated by arrows). Two layers of melt features associated with ash layers are found at the top of the lower core section.

The stratigraphic features indicate that surface melting occurs at this glacier despite its cold environment. The drilling site is thus considered to be located at the percolation zone of Reference BensonBenson (1962). We call the refrozen melt layers melt features because they sometimes appear as vertical ice glands. There are only two possible causes for melting in this glacier: (1) the air temperature occasionally exceeds 0°C in summer, and (2) volcanic ash covers the snow surface and induces melting by reducing the albedo of the snow surface. Support for the warm-temperature cause is the correlation between the summer atmospheric (700 hPa) temperatures over the Kamchatka peninsula and melt-feature percentages in the 27 m ice core recovered at BH1 (Reference Shiraiwa, Murav’yev and YamaguchiShiraiwa and others, 1997). The volcanic-ash cause occurs unpredictably and induces melting even at temperatures as low as −10°C. This implies that the occurrence of a melt feature does not necessarily indicate that a warmer summer occurred.

We have constructed two series that show how melt features vary with depth in the ice core. The melt-feature percentage (MFP) was calculated according to the following relation (Reference KoernerKoerner, 1977; Reference Kameda, Narita, Shoji, Nishio, Fujii and WatanabeKameda and others, 1995):

where S _i refers to areas with melt features, S _f refers to areas with firn and bubbly layers after the pore close-off depth, 0.9 (Mg m⁻³) is the density of the melt features, and ρ _f is the density of firn and bubbly ice (Mg m⁻³). These areas were identified on a flat surface cut along the ice and firn cores. The unit length for the measurement of MFP was 1 m throughout the ice core.

The original MFP profile in Figure 6 was made without paying attention to ash layers. All the less bubbly layers were counted as melt features. The climatic MFP in Figure 6 excluded possible influences of volcanic eruptions on the formation of melt features by subtracting the ice layers associated with ash layers. This is because we considered the less bubbly layers associated with ashes not to be of climatic origin, but instead due to the volcanic eruptions. The location of ash layers in the melt features is variable: some ash layers appear in the lowest part of the melt features (Fig. 5), and others are located in either the upper or the middle parts. For all varieties, we simply subtracted the ice layers including ash layers in the calculation of climatic MFP. Therefore, this is a first approximation to the past summer temperatures, and it must be checked in the future by comparing with a stable oxygen isotopic profile.

Fig. 6. Distributions of (a) original MFP, (b) MFPexcluding ash layers, (c) number of ash layers within an ice-core length of 1 m, and (d) inclination angle (°) of the ash layersfrom the horizontal plane. For the MFP, running average curves of 7 mare also shown.

In the original MFP profile, several peaks of high MFP appear throughout the entire depth. Prominent peaks were found at depths of 160, 105, 85, 70 and 60 m, where the MFPs exceeded 50%. In these peaks, a possible reason for the high MFP was a volcanic eruption since many of the peaks disappeared after subtracting the melt features associated with ash (cf. the climatic MFP in Fig. 6). This means that the activity of nearby volcanoes significantly affected the physical properties of the ice core in the crater glacier.

4.2. Tephrochronology

Macroscopic observations (Fig. 6) indicated a total of 328 ash layers in the 211.70 m ice core. They are distributed throughout the depth of the ice core. The appearances of the ash layers are variable, from a densely compacted thick one to a sparsely scattered aggregate of ashes. The thickest ash layers were those observed at 35.49, 86.44, 102.82 and 138.45 m, and each was at least 1.0 cm thick.

The mineral composition of the ashes enabled us to determine the sources of the ash layers at depths of 12.04, 35.49 and 102.82 m. The whitish, pumice-like fine ashes at 12.04 and 35.49 m depth contained plagioclase, pyroxene and hornblende. These are typical components of ashes erupted from Bezymianny volcano, which is approximately 14 km southeast of the glacier. The last catastrophic eruption occurred in March 1956 (Reference Flerov, Ovsyannikov, Fedotov and MasurenkovFlerov and Ovsyannikov, 1991), and is identified as a sequence of ash layers spanning the ice-core section between 35.49 and 35.30 m. The ice cores in this section show clear ice with very few bubbles, indicating that rapid melting occurred near the ash deposition. The average accumulation rate from 1956 to 1998 is thus estimated as 0.54 m a⁻¹ w.e. by using the depth-density information provided below.

The ash at 12.04 m depth was also identified as Bezymianny ash since one of the authors (Y.M.) made a continuous pit observation at this glacier during 1985/86 and found this layer near the surface at that time (Reference Murav’yev and SalamatinMurav’yev and Salamatin, 1989). Ash layers at depths of 1.43 and 0.81 m were identified through our continuous pit observations as Bezymianny ashes erupted on 9 May and 5 December 1997.

The mineral composition of ashes at 102.82 m contained plagioclase, olivine and pyroxene, which identify them as ash from Klyuchevskoi volcano located just beside Ushkovsky volcano. This is one of the most active volcanoes in Kamchatka, with eruptions almost every year. Among these eruptions, that in 1829 was extremely hazardous. In the ice core, we found many ash layers that probably originated in Klyuchev- skoi volcano. The ash at 102.82 m depth was the thickest and most concentrated, so we attribute it to the 1829 eruption.

Besides the ash layers, we observed clear-ice layers containing no bubbles but scattered and rounded rock fragments in the lower part of the ice core. These are schematically shown as dots in Figure 3. They started to appear at 154 m depth and then appeared at 179, 195, 198, 200 and 208 m. The thickness of each horizontal layer varied from 10 to 100 cm, and the layers are clearly distinguished from the neighboring layers. We believe that the layers were most probably accreted at an ice–bedrock interface where bottom melting occurs sporadically along the glacier bottom. The refrozen water at the bottom might have been accreted into the glacier after entraining rock fragments from the bottom.

We measured the inclination angle of each ash layer from the horizontal plane normal to the core axis. It was impossible to determine the azimuth of the core, so we measured the maximum polar angle for each ash layer (Fig. 6). Horizontal ash layers were found from the surface to 180 m depth, whereas ash layers were always inclined, some as much as 30° from the horizontal plane, at deeper levels. Although inclined layers were found at shallower depths, such layers are not necessarily caused by glacial flow; some of the ash layers must have been deposited at an angle to the surface. Because no horizontal layers are detected below 180 m, we conclude that only depths below 180 m indicate noticeable influence of rotational movement of the glacier that suggests shear strain.

4.3. Bulk density

Figure 7 shows the bulk density distribution with depth. There is considerable scatter in the profile above the pore close-off depth at around 55 m because the bulk measurements were made for each core segment without distinguishing firn from ice. The close-off depth at 55 m was almost the same as the 58 m predicted by Reference Shiraiwa, Murav’yev and YamaguchiShiraiwa and others (1997) using Reference Herron and LangwayHerron and Langway’s (1980) densification model. The latter estimate used the depth–density data for the upper 27 m obtained at BH1 on the same glacier.

Fig. 7. Depth–density relationship for the ice-core data obtained at K2. The solid line is the mean-square approximation.

The entire part of the profile of the present bulk density ρ can be fitted, by mean-square approximation, as

where ρ _i is the density of pure ice (918 kg m⁻³), c _s is the ice porosity at the surface (0.55), h is the depth from the glacier surface in meters, and γ is a coefficient (0.038 m⁻¹). The values of the parameters are slightly different from those obtained by Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others (2000) (Table 1). The difference is ascribed to the difference of the location where the ice cores were obtained and, more directly, to a more detailed density analysis of the ice core in this study than in the previous one.

The total thickness of the glacier at K2 was calculated as 207 m w.e. and 226 m ice equivalent from the density data in Table 1. These values will be used to construct the depth–age relationship at K2 in the final part of this paper.

4.4. Crystal-size and -orientation fabrics

Figure 8 shows photographs of the vertical thin sections in cross-polarized light and the Schmidt equal-area net plots of the crystal c-axis orientations projected on the horizontal planes. The center of the circle represents the vertical direction in the Schmidt equal-area net.

Fig. 8. Cross-polarized photographs of vertically cut samples and c-axes orientation fabrics projected for the lower hemisphere of Schmidt equal-area nets approximately every 20 m along the ice core. The number of samples for the c-axes orientation measurement are in the right upper corner of each diagram.

We did not observe any systematic change in the size of crystals with depth, as is the case in most cold glaciers and ice sheets. The temperature of the glacier is highly variable, from −15.8°C at 10.00 m to −4.2°C at 211.70 m, as discussed in the next section. This temperature range favors polygoniza- tion and recrystallization as mechanisms that inhibit crystal growth, although we observed neither strain shadows nor sutured grain boundaries above sample No. 460 (202.03–202.11 m). These features suggest polygonization and dynamic recrystallization, respectively. The crystals in sample No. 483 (211.42–211.50 m) are slightly elongated in the direction of about 45° from the core axis, which suggests shear stress at this depth. This is why the influence of deformation on grain-size might explain the lack of appreciable grain growth with depth. Also, a relatively high concentration of chloride and sulfate ions in the ice might have influenced the crystal growth by impeding grain-boundary migration (Reference Alley, Perepezko and BentleyAlley and others, 1986); this is because the average concentrations of 553 and 3468 μg L⁻¹ of each ion in the core from 0 to 110 m depths (Shiraiwa and others, unpublished information) are high enough to support this effect.

In contrast, the c-axis orientations seem to change with depth. In the upper 160 m of the core, the c axes appear to be quasi-uniformly distributed (Nos. 137, 188 and 376) and, in some cases, show a weak girdle-type cluster around a vertical plane (Nos. 220 and 322). The c axes start to have a preferred orientation below 180 m. At first, they tend to concentrate in a single maximum at depths from 182 to 202 m (Nos. 413 and 460), and then they have a single maximum at 211 m (No. 483) where the preferred orientation is inclined approximately 22° from the horizontal plane.

A great girdle-type fabric often appears in a convergent flow field of vertical compression with longitudinal extension such that the direction of the circle–girdle axis is perpendicular to the flow direction. This occurs in ice cores at Vostok and Mizuho in Antarctica (Reference Fujita, Nakawo and MaeFujita and others, 1987; Reference Lipenkov, Barkov, Duval and PimientaLipenkov and others, 1989), but here we cannot determine the flow direction from elongation of the crystals and information on the natural geomagnetization. The K2 site is slightly downstream from the center of the crater, and the ice thickness increases considerably along the flowline from the dome to the K2 site (Fig. 3). Therefore, it is most likely that the girdle pattern was formed by a flow field of compression in both the flow (x) and vertical (z) directions, with extension to the transverse (y) directions to the flow; that is, divergent flow.

It is unusual to see a fabric starting to develop already in the uppermost 100 m. The fabric strength seems to be mainly determined by the total vertical strain, and because the vertical strain rate is comparatively high at this location (0.54 m a⁻¹/207 m = 2.6 × 10⁻³ a⁻¹), fabrics should evolve much more rapidly with depth and time than in ice cores from the large polar ice sheets.

The single maximum that appeared in the deepest part of the cores can be produced by simple shear, which is the most probable flow field near the bottom (88% depth below the surface). However, the compression axis may not be vertical but inclined to approximately 22° from the horizontal plane. This might indicate a complex flow field near the bottom of the glacier due to the concave profile of the crater glacier. The layers of ash that are inclined as much as 30° below 180 m (Fig. 6) are concomitant with the fabric patterns, suggesting a rotating flow with the simple shear at this depth.

6.1. Basal condition of the crater glacier

In previous theoretical thermodynamic analysis (Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000), we estimated the bottom melting rate at BH1 as 0.11 ± 0.004 m a⁻¹. After drilling the ice core at K2, we obtained more complete data concerning the local physical properties of the glacier, as described in sections 4 and 5. We now examine the basal condition using the newly obtained dataset listed in Table 1, and propose a more detailed and precise estimate of the geothermal heat flux for the K2 site and thereby the depth–age relationship at K2.

Owing to the linearity of the temperature profile at K2, we extrapolate the profile to the deepest part. The temperature gradient of 0.051 °Cm⁻¹ used for the extrapolation to the glacier bottom was obtained from the lower 112 m of the profile between 99.60 and 211.70 m, where the profile was straight. The bottom temperature at 240 m is thus calculated as −2.8 ± 0.1°C. This value is colder than the melting temperature, even if we take into account that the melting point is depressed due to pressure by 0.15–0.20°C. Therefore, the bottom of the glacier at K2 is probably frozen to the bed.

The volcanic heat flux can also be estimated. The volcanic heat flux q ₀ is given by the conventional heat-conduction equation q ₀ = λ_i(∂T/∂z)_bottom, where the thermal conductivity λ_i is 2.3 W m⁻¹ K⁻¹ for basal temperatures in the lower 100 m of the glacier. As a result, we obtained a volcanic heat flux q ₀ of 0.12 ± 0.01 W m⁻². This is approximately 1.5–2.6 times larger than the average heat flux on the continents (0.046–0.077 W m⁻²; Reference PatersonPaterson, 1994), and one to two orders of magnitude lower than predicted for this glacier by theoretical considerations (Reference Murav’yev and SalamatinMurav’yev and Salamatin, 1989; Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000).

6.2. Depth–age relationships

Earlier we derived a simplified analytical solution for the depth–age relationship at the glacier in the Gorshkov crater using the melting condition at the bottom (Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000). In this solution, the age t of the ice for an ice-equivalent thickness Δ of the glacier is

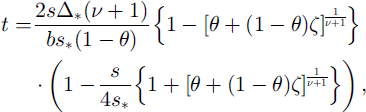
where s is the distance from the ice dome, s_* is the distance from the ice dome to the deepest point K2 (650 m), Δ_* is the ice-equivalent thickness at the deepest point K2 (223 m), v is the exponent in the approximation for the ice-flow-tube width (here taken as v = 1 for divergent radial flow), ζ is the normalized vertical coordinate as expressed by distance from the glacier bottom measured in terms of equivalent thickness of pure ice, b is the annual accumulation rate of ice (0.60 m a⁻¹), and θ is the relative melt rate.

In this solution, we used a relative melt rate θ of 0.25. This is the ratio between the bottom melt rate and the surface accumulation rate expressed as an area mean over the glacier. In this case, the maximum age of the bottom ice at K2 was calculated to be about 610 years (AD 1388) (Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others, 2000).

We now know that the geothermal heat flux is not uniform along the flowline. Thus, we should revise θ so as to fit these new data. To estimate the mean melt-rate ratio θ, we might assume that along the first half of the flowline the local melt rate varies from 1 to 0 and then remains 0 until K2. These assumptions are based on the three considerations mentioned in the previous sections: (1) the basal melt rate ∼0.33 ma⁻¹ (Reference Murav’yev and SalamatinMurav’yev and Salamatin, 1989) is nearly equivalent to the accumulation rate near the rim where the ice cave exists, (2) the basal melt rate is most probably zero at K2, and (3) the uppermost accreted ice layers, described in section 4.2, might have originated in the region where the melted bottom changed to a frozen bottom at s = 300 m in Figure 3. This is the “coldest-bottom scenario”. Because the melting–freezing boundary cannot be decided precisely with the available dataset, we also show the “warmest-bottom scenario” This case assumes that only the deepest part of the glacier is frozen to the bed, and the melting–freezing boundary was located at s = 560 m.

The mean melt rate θ for the two limiting cases is calculated from

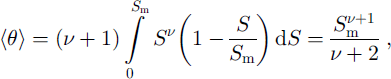
where S _m is the ratio between the distance to the melting–freezing boundary and the distance to the site of consideration. In this case, we assume the local melt rate varies from 1 at the crater rim (ice dome) to 0 at a distance of 300 m (the coldest) or 560 m (the warmest). The former case locates the melting-freezing boundary at the same level at which the accreted ice layers start to appear in the ice core at K2 (Fig. 3). In our case v ≈ 1 (divergent flow); therefore, S _m equals 0. 462 for the coldest-bottom scenario and equals 0.862 for the warmest-bottom scenario. As a result, the estimate of θ becomes 0.07 for the coldest and 0.25 for the warmest-bottom scenario.

We constructed two versions of the depth–age relationships at K2 with the newly obtained boundary conditions (see Table 1; Fig. 10). The depth-age relationship obtained by θ = 0.07 predicts significantly different ages in the lower parts in comparison with those predicted using θ = 0.25. The ages of the bottom of the glacier at K2 and the deepest point of the borehole were 829 (AD 1169) and 603 (AD 1395) years for the coldest-bottom scenario, and 639 (AD 1359) and 511 (AD 1487) years for the warmest-bottom scenario, respectively. The older ages in our coldest-bottom scenario are mainly the result of bottom compression due to a more extensive frozen bottom.

Fig. 10. Two tentative depth−age relationships constructed with newly obtained bottom boundary conditions (θ = 0.07 and 0.25) according to the model by Reference Salamatin, Murav’yev, Shiraiwa and MatsuokaSalamatin and others (2000). The positions of three dated ash layers are also shown.

The two possible depth–age relationships can be evaluated against the dated ash layers found at depths of 12.04 m (AD 1985), 35.49 m (AD 1956) and 103.0 m (AD 1829) m. In the coldest-bottom scenario, each depth of the dated layers gives AD 1986, AD1954 and AD1813, and the differences between the real dates and the predictions increased from l year at 12.04 m to 16 years at 103.0 m, whereas in the warmest-bottom scenario each depth of the ash layers is dated as AD 1986, AD 1955 and AD 1820, respectively.

The results show that the warmest-bottom scenario gives the better estimates. The depth–age relationship given by the warmest-bottom scenario can thus provide a first basis in considering the age, and therefore the thinning history, of the ice core. Equation (3) assumes steady-state conditions with a constant accumulation rate and constant basal boundary condition. The input of newer data, such as accumulation-rate history, should reduce the small discrepancy that remains.