Introduction
The West Antaretic ice streams (Reference BentleyBentley, 1987) move ~10-100 times faster than the adjacent non-streaming ice sheet (Reference BindschadlerBindschadler and Scambos, 1991; Reference WhillansWhillans and van der Veen, 1993). In the discussion of the cause of this rapid movement the main current focus is on shear deformation of unfrozen, water-saturated subglacial till (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1986, Reference Alley, Blankenship, Rooney and Bentley1987, Reference Alley1989; Reference MacAyealMacAyeal, 1989, Reference MacAyeal1992; Reference KambKamb, 1991), The alternative possibility of rapid basal sliding, proposed originally by Reference RoseRose (1979!, has been discounted theoretically Reference AlleyAlley, 1989). Although the presence of soft basal till has been documented (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990; Reference Tulaczyk, Kamb, Scherer and EngelhardtTulaczyk and others, in press), there has been no detection or measurement of either basal sliding or the hypothesized shear deformation of the till. In this paper we present results of measuring the basal sliding component of ice-stream motion, and thus indirectly also the rill-deformation component. The measurement is made on lee Stream B in West Antaretica.
The nature and cause of the rapid ice-stream motions is of interest and importance both as a fundamental feature of glacier mechanics and because the rapid motions may contribute to instability of the ice sheet, with possible consequences in the rise of world-wide sea level (Reference AlleyAlley, 1990; Reference BindschadlerBindschadler. 1991: Reference MacAyealMacAyeal, 1992; Reference AlleyAlley and MacAyeal, 1993).
Measurement Technique
The basal sliding measurement is done in a borehole drilled through the ice to the top of the underlying unfrozen till by the hot-water jet drilling method. To measure basal sliding we use a “tethered stake" instrument that is similar in principle to the “drag spool" system described by Reference Blake, Clarke and GérinBlake and others (1992, p.3951 and Reference Blake, Fischer and ClarkeBlake and others (1994). A stake is driven into the top of the till and moves away from the hole if there is a discontinuity in motion at the ice-till interface (Fig. 1). The stake is attached by a nylon line (the “tether”) to a metering unit it) the borehole, which pays out the tether, meters the length payed out, and reports this count to the surface via an (armored) electrical cable. The tether (multi-stranded nylon line of width 0.25 mm and strength 7 kg) is fed from a storage spool in the metering unit, passes 1½ turns around a small metering spool (diameter 14.6 mm) and then down and out lo the stake. A schematic diagram of this arrangement is given in Figure 2, with principal dimensions of the instrument indicated.
Rotation of the metering spool is sensed by a Reed relay (Anonymous, 1997, p. 797), which is actuated by the magnetic fields of two small permanent magnets mounted on the rim of the metering spool at opposite ends of a diameter (Fig. 2). As the spool rotates and the magnets in turn pass by the Reed relay, the output of the sensing circuit jumps abruptly back and forth between the values 0.001 ± 0.001

Fig. 1. Geometry of the tethered stake experiment to measure basal sliding, (a) in the absence of distributed shear in the sub glacial till, and (b) in the presence of such shear. Relative to a fixed coordinate system the ice is moving to the left by basal sliding and till deformation. The diagrams show the position of the stake and the tether line at a sequence of times 1, 2,..., 5 (arbitrary time units), in a coordinate system moving with the ice. At time 1 the stake has just been released from the metering unit and has started moving towards the right relative to the ice; the top of the stake moves at the sliding speed, which is indicated schematically by the upper open arrow at lower left. The friction in the tether pay-out system is assumed to be small enough in relation to the till strength that the tension in the tether line does not cause the stake to till. In (b), tilting of the stake is caused by the distributed shear deformation in the till, with the sense shown by the pair of half-headed arrows at lower right and by the open arrows at lower left. By the time the stake has rotated to a near-horizontal position (time 5 in (b) ) its motion relative to the ice includes the shear displacement from the ice sole down to the level of the stake in the till.
V and 1.05 ± 0.15 V. The voltage jumps, which we will here call “pulses”, are spaced approximately 90° of spool rotation apart (four pulses per revolution). The circumference of the metering spool is 46 mm, and each pulse therefore signals the pay-out of 11.5 mm of line (on average) since the last pulse. The output voltage is recorded by a data logger every 2 min, which allows sliding rates up to 8.3 m d-1 to be measured, corresponding to one pulse every 2 min. The friction of the storage spool and metering spool is very low, corresponding to a very small resistance to pulling out the tether line; this resistance has not been measured but we judge it to be smaller than 0.1 N.
The metering unit also has the function of holding the stake while the assembly (metering unit plus stake) is lowered into the borehole, and then releasing the stake once it is pushed into the till by the weight of the metering unit above. The holding and release mechanism is shown in Figure 2. When the stake comes to a stop in the till, the metering unit slides down over the stake’s two retainer rods, and the latch pins slide along the rods’ beveled ramps, pushing the latch pins outward. When the pins have been pushed far enough out, the spring-loaded balls snap into the grooves in the pins, locking them in the open position. When the metering unit is raised 6 cm, the stake, stuck in the sticky till, is not pulled up with it (because the latch pins are open) and is released from the metering unit; it is now able to move sidewards if basal sliding occurs. The release action is monitored from the surface, because the raising of the metering unit to release the stake pulls out at least 4 cm of tether if the stake remains stuck in the till and is not pulled up with the metering unit.
As Figure 1b shows, the tethered stake motion provides a good measurement of basal sliding, with little contribution to the measurement from shear deformation in the till, provided that the point of attachment of the tether to the stake is close to the top of the till. We expect that emplacement of the stake in the till by the method described above will place the stake approximately in this position. This expectation is based on our experience in boreholes to the bed of Ice Stream B, namely, that a blunt cylindrical object like the metering unit will penetrate under its own weight only a few centimeters into the till. A complication relative to Figure 1 is introduced by the retainer rods, which slick up 10 cm above the tether attachment point at the top of the stake (Fig.2). This requires that if the stake is vertical the attachment point must be placed 10 cm below the ice in order that the retainer rods not catch on the basal ice as the stake moves away from the hole. However, in the actual measurement sequence described below the retainer rods probably did catch, as discussed in the section “Interpretation”.
The tethered stake metering unit also contains a pressure transducer, so that variations in basal water pressure can be followed at the same time as basal sliding.
Measurements in Ice Stream B
In December 1995, a basal sliding measurement sequence was carried out with the tethered stake in borehole number 95-1, of depth 1026.8 m, at 83.4551°S, 137.7793°W. The location is 400 m from camp UpB ’95 (“new UpB”), within Ice Stream B2 about 10 km north of its south margin (Fig. 3).
Further detail on the location has been given by Reference Engelhardt and KambEngelhardt and Kamb (1997, fig.2a). The ice-stream surface velocity at the borehole location is taken to be 1.18 ± 0.01 m d-1, based on GPS measurements at UpB’95 in November 1991-November 1992 by Reference HulbeHulbe (1994. p. 74); nearly the same velocity, 1.21 md-1, was obtained by Reference Whillans, Bolzan and ShabtaieWhillans and others (1987) (see also Reference WhillansWhillans and van der Veen, 1993) at nearby UpB ’84 in 1984-86, indicating that the velocity is practically constant.

Fig. 2. Detailed features of the tethered stake instrument, shown schematically, with principal dimensions indicated the lower half shows the stake in perspective view, and the upper half shows in orthographic section (somewhat schematic) the bottom part of the metering unit with the two beveled retainer rods, of diameter 0.6cm, plugged into the holding-and-release mechanism. The cross-hatched rectangle adjacent to the magnet labelled “NS" on the metering-spool rim shows schematically the location of the Reed relay, it is separated from the spool and magnets by the wall (not shown ) of the pressure-tight case of the upper part of the metering unit, which contains the electronics and the pressure-transducer body. The latch pins are shown in the closed position, in which they hold the hook-shaped lop ends of the two beveled retainer rods and keep the stake from dropping away from the metering unit until the latch pins are pushed open as described in the text.
On the first attempt, the stake did not release when the metering unit was raised, as described in the last section. On the second attempt, the stake was planted deeper by lowering the instrument faster into the till. The release of the stake then worked, as indicated by output pulses received as the metering unit was raised. For the first 10 hours thereafter- no pulses were received, except for pulses generated when the unit was raised, by amounts of about 1 cm, which was done three additional times to test the unit for its response.
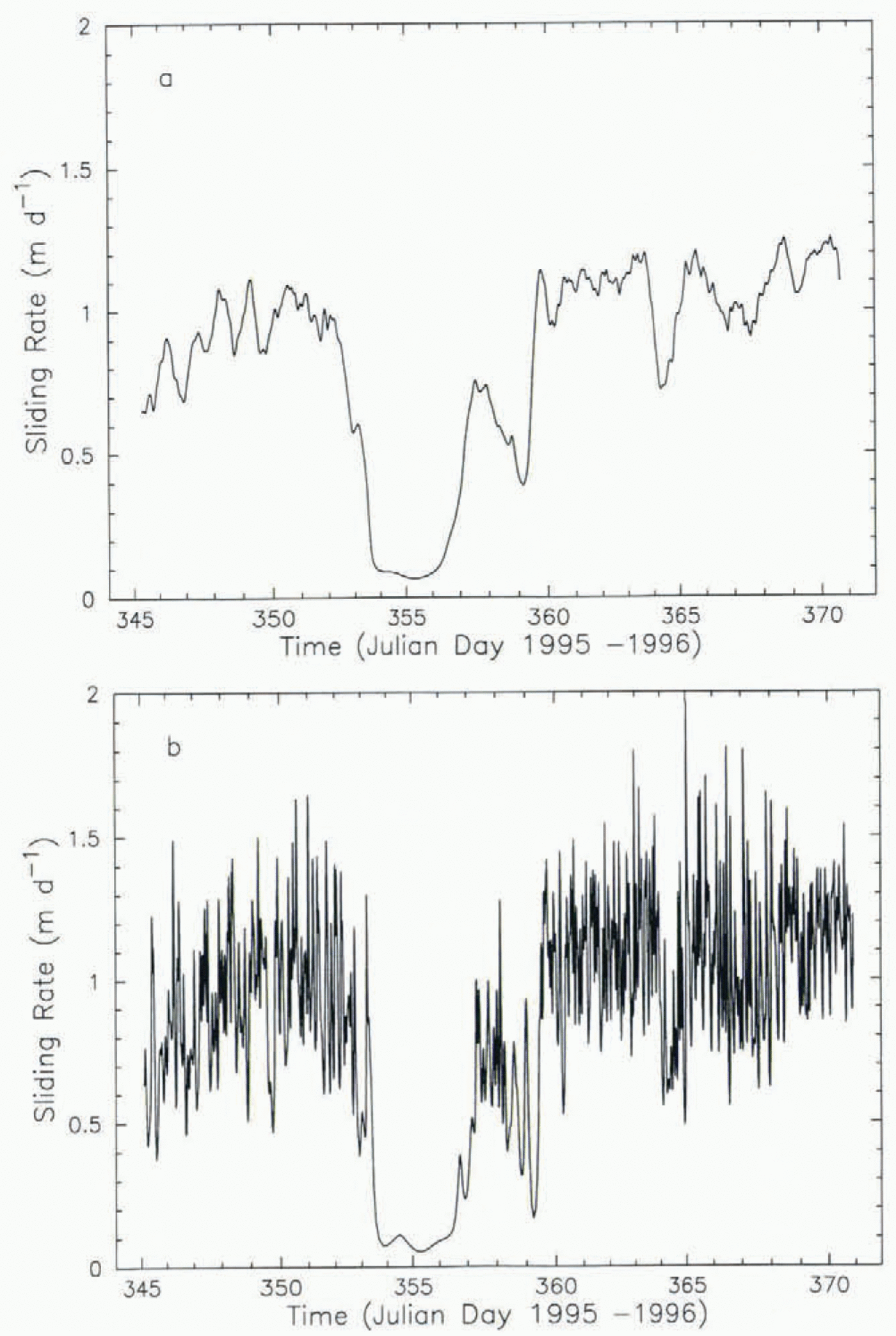
Starting at 0039 h on Julian Day (J.D.) 345, spontaneous pulses began to be received. The record of tether pay-out is given in Figure 4 as a function of time. It ran for 26 days and terminated when the 21 m of tether line originally wound on to the storage spool was fully paid out. In the following presentation of results, we generally equate tether pay-out with basal sliding. The uncertainties in doing this are discussed in the next section (“Interpretation”). We use the words “apparent basal sliding" where some particular uncertainty in the relation between tether pay-out and sliding is involved.
Figure 4 shows an 8 day initial period of rapid motion (c. 0.9 m d-1,J.D. 345-353), then a 3.5 day slow period (c. 0.1 m d-1, J.D. 353.5-357), an intermediate period (average O.6 m d-1, J.D. 357 359.4), and finally an 11 day period of rapid motion ι c. 1.1 m d-1, J.D. 359.4-371). In the last 2 days of the experiment, the apparent sliding rate reached 1.17 m d. The rapid sliding motions are 75% to essentially 100% of the ice-stream surface motion of 1.18 m d-1. The average rate of apparent sliding motion from J.D. 345.0 to 370.9 is 0.82 m d-1, which is 69% of the surface motion.
For comparison, the sliding rates measured in Trapridge Glacier, Canada, by Reference Blake, Fischer and ClarkeBlake and others, (1994, p. 598) were in the range 0.04 0.08 md-1 and represented 50-100% of the surface motion.
Figure 5a gives the apparent sliding rate vs time, obtained by differentiation of a cubic-spline interpolation of the data in Figure 4. Figure 5a shows that there is much jerky motion or else high-frequency noise in the time intervals between successive pulses. This jerkiness or noise is greatly reduced by smoothing the curve in Figure 5a with a 0.5 day running mean, which gives Figure 5b. However, even with this smoothing, pronounced variations in sliding rate are indicated in addition to the 3.5 day slow period noted above.

Fig. 3. Location of borehole 95-1 at which basal sliding measurements were made (solid dot at 83.5 °S, 138° W). The inset at the upper left shows location of map frame relative to the Antaretic continent
The contribution to the ice-stream motion from shear deformation of till beneath the level accessed by the tethered stake is simply the surface motion minus the measured sliding rate. The contribution of ice deformation to the motion is negligible. This follows because the basal shear stress is very low-0.06 bar according to the model of Reference Echelmeyer, Harrison and MitchellEchelmeyer and others (1994, fig. 5), ≤0.08 bar according to Reference Jackson and KambJackson and Kamb (1997, section 6). The corresponding ice-flow velocity calculated from the 0°C How law of Reference PatersonPaterson (1994, p. 97) is < 1.6 ± 10 -4m d-1.

Fig. 4. Measured apparent sliding distance from tether pay-out in borehole 95-1 as a function of time. The record starts with release of the tethered stake at J.D. 344.60. 3 cm of apparent sliding produced artificially by raising the metering unit three times during the interval J.D. 344.6- 345.0 has been omitted from the record.
The pressure-transducer record (basal water pressure vs time) is given in Figure 6. The pressure scale (ordinate) is subject to a calibration problem. Our standard in-situ pressure calibration of the instrument as it is lowered into the borehole was inadvertently omitted. A preliminary calibration made much earlier, in the laboratory in Pasadena, does not give the correct pressure when applied to the transducer output signal at two times when the pressure is known from independent measurement, namely at the start of the run (on J.D. 344) and near the middle of the run, on J.D. 355. The independent measurements were made by a pressure transducer that indicated the depth of the water level in borehole 95-1 and, later, in borehole 95-2, which was located 10 m from borehole 95-1 and doubtless connected to the same basal water system. These measurements, combined with the borehole depth, indicate basal water pressures of 91.1 and 91.4bar, respectively, whereas the tethered-stake pressure transducer with preliminary calibration indicated 100 and 98 bar respectively, in error by about 10%. The reliable values 91.1 and 91.4 bar are close to the ice-overburden pressure of 91.2 bar, which is entirely typical of basal water pressure observed in boreholes in Ice Stream B (Reference Engelhardt and KambEngelhardt and Kamb, 1997), whereas the erroneous values of 100 and 98 bar would indicate an overpressure (excess of basal water pressure over overburden) of 7-9 bar. Such a high overpressure is seen only in boreholes that have not reached (he bed and have not connected to the basal water system; upon connection, the overpressure always drops rapidly to near 0 (maximum 0.3 bar) (Reference Engelhardt and KambEngelhardt and Kamb, 1997, table 1). In this context, the maintenance of a 7-9 bar overpressure for 24 days, which the preliminary calibration would indicate, is extremely doubtful, and in any case is ruled out by the reliable pressure values. We therefore use the reliable value 91.1 bar as a calibration point and correct the preliminary calibration by adjusting the slope of the (linear) pressure vs output voltage relation so as to fit the calibration point. 1’he result is Figure 6.

Fig. 6. Basal water-pressure record from the tethered stake instrument in borehole 95-1. The pressure scale (ordinate) is as explained in the text.
In Figure 6, the near constancy of the indicated basal water pressure (≈90bar) over the period J.D. 344-369 is consistent with a nearly constant pressure of 91.1-91.3 bar observed by borehole water-level measurement in borehole 95-1 during the period J.D. 338-344 that immediately preceded insertion of the tethered stake. A major exception to the nearly constant pressure is the 2 day interval of substantially reduced pressure starting on J.D. 350. Figure 6 also shows three or four minor diurnal fluctuations near the beginning of the record, minor irregular fluctuations thereafter and 0074wo large but short drops in pressure at the end.
About 10 km downstream from borehole 95-1, a brief preliminary measurement of basal sliding was made in borehole 89-5 on 5 January 1990 near camp UpB’84 (“old UpB”). It was done wit h a non-electrical tethered stake a precursor to the electrical tethered stake instrument described above. Tether pay-out of 20 cm in 2.4 hours at an approximately steady rate of 2.0 m d-1 was observed, after which the pay-out stopped, presumably because the tether cable, which ran from the bed to the surface, became frozen to the borehole wall.
Interpretation
The tethered stake records in Figures 4 and 5 indicate that basal sliding is the predominating process that contributes to the rapid ice-stream motion al the site studied. Several aspects of this conclusion need to be explored:
1. In treating the tether motion as a measure of basal sliding, we must be clear that this means basal sliding sensu lato (s.l.) but not necessarily sensu stricto (s.s.). Basal sliding s.s. is a sharp discontinuity between the motion of the ice mass and the top of the immediately subjacent till. Basal sliding s.l. is sliding s.s. plus whatever relative motion may occur across a thin shear zone in the till immediately below the top. How thin this shear zone has to be to qualify for inclusion in basal sliding s.l. has not been defined and would seem to be a matter of choice. Often in the glaciological literature the term “basal sliding" is used to mean the full basal motion including the full contribution from sub-sole deformation at all levels (Reference RobinRobin, 1986, p. 490). We prefer to restrict sliding s.l. to mean sliding s.s. plus any contribution from sub-sole shear that cannot be separated from sliding s.s. by the resolution of our means of observation, which was designed with the objective of minimizing the sub-sole till shear contribution that is included in the measurement. The thickness of the “inclusion zone" in the till the zone from which the included contribution comes is here called the “inclusion thickness”. In the tethered stake experiment, the inclusion thickness is approximately the perpendicular distance from the base of the ice to the tether attachment point on the stake. Ideally, this could be a few millimeters in the initial tether geometry of Figure 1 but, because of the retainer rods (as discussed earlier), the inclusion thickness has to be increased to about 10 cm if the stake is near vertical. If the stake rotates lo a horizontal position due to distributed basal shear in the till (Fig. lb), the inclusion thickness increases further to approximately half the stake length, about 25cm. On the other hand, if the stake initially exits the borehole in the way shown in Figure 7 (see below), the inclusion thickness will be about half the width of the stake, 3 cm.
2. 11 the stake is not emplaced deep enough in the till, it will initially be trapped in the borehole and will not begin to move away from the hole (Fig. 7). The tendency for this to happen is increased by the presence of the retainer rods sticking up above the top of the stake (Fig. 7). While the stake is trapped in this way, little or no tether line will be payed out. If the stake protrudes down far enough into the till below the level of the base of the ice and, if there is basal sliding or till shear, the stake may be rotated and translated by the sliding or shearing motion and may ultimately exit the hole as shown in Figure 7b e. Such rotation and exit is similar to what has actually been seen in the behavior of rocks at the bottom of boreholes in a sliding glacier (Reference Engelhardt and HarrisonEngelhardt and others, 1978. figs 2-4). This, we infer, is what happened at the beginning of the tethered stake experiment. The evidence for stake entrapment is the lack of tether movement in the first 10 hours after the stake was emplaced in the till. The lack of movement cannot be ascribed lo instrument malfunction, because four tests in which the metering unit was raised 1 or a few centimeters showed that the instrument was active and the tether was taut. The subsequent abrupt onset of tether pay-out indicated when the stake escaped from the hole and the registration of basal sliding started, according to this interpretation.
3. The above interpretation implies that once the stake escaped from the borehole it was very close to the base o(the ice (Fig. 7e), so that the inclusion thickness was about 3 cm, as noted in item 1 above. A larger inclusion thickness -10 or 25 cm as explained in item 1 — would be obtained if the retainer rods caught only slightly on the borehole wall, or not at all, so that the stake escaped the borehole in a near-vertical position (as in Figure 1), However, catching only slightly would not explain the initial 10 hour period of no-tether motion, and for this reason we incline to accept instead the model in Figure 7.

Fig. 7. Qualitative model of tethered stake movement in the course of the basal sliding observations in borehole 95-1. The retainer rods at the top of the stake (Fig. 2) are shown. Diagrams (a), (b),..., (f) show schematically the configuration at successive times, analogously to 1, 2,..., 5 in Figure 1. In (a) the stake has been emplaced at a higher than intended level and is trapped against the wall of the hole. In (b)-(d), lateral drag from the till, due to the basal sliding motion (arrows) and/or till shear, tills the stake. In (e) the stake has escaped from the hole, and the tether reports the sliding motion as the stake slides along very cluse to the base of the ice. In (f) the stake catches on a protruding rock clast and hangs up; it no longer reports the full sliding motion. Later (not shown) the stake comes loose from Ike clast and moves on to the right, again reporting the sliding motion.
4.Another consequence of the closeness of the escaped stake to the ice is that the stake is subject to becoming caught and hung up against basal rock clasts that may protrude down from the ice and plow through the till (Fig. 71). Because of this possibility, the slow tether motion during J.D. 353.5-357 can be interpreted either as a slow-down in actual basal sliding or else as an artifact due to the stake getting temporarily hung up against the sole. A fact consistent with the latter interpretation is the rather abrupt onset of the slow apparent motion as seen by the kink at J.D. 353.5 in the curve in Figure 4. The somewhat abrupt and jerky resumption of movement seen during J.D. 357-359 in Figures 4 and 5 seems consistent with multiple small hang-ups.
5. From Figures 4 and 5a, it might appear that the tether motion never went completely to zero during the 3.5 day slow period, which might argue against the hang-up interpretation. In fact, however, during J.D. 353.3—356.7 there were eight intervals of time during which the tether reported no apparent motion (less than 1.1 cm ) for periods of 4 hours or more, including one such period of 13.5 hours. For practical purposes, the stake was completely stopped during these times. These features are not resolved at the scale of Figure 4 and are suppressed by the smoothing (spline) in Figure 5a. On J.D. 359, at the end of the 2.4 day period of intermediate apparent sliding; there was a period of 6.4 hours during which only one pulse (1.1cm of motion) was reported; it can be seen in Figure 4 and probably represents another hang-up.
6. Because the initial part of the tether-motion record (no motion for the first l0 hours) implies the type of stake movement shown in Figure 7, with the possibility of hang-up like that shown in Figure 7f, and because we are reluctant to believe that the ice-streaming system is so unstable as to switch rapidly between slates of almost exclusively basal sliding and almost exclusively till deformation, we provisionally conclude that the 3.5 day slow period is an artifact of stake hang-up on the sole as discussed above. In that case, the period(s) of hang-up should be omitted in obtaining the average basal sliding rate from the data in Figure 4. An average sliding rate of 0.98 m d-1 (83% of the total motion) is obtained by averaging the data from the time intervals J.D. 345.0-353.5 and J.D. 359.4-370.9, which omits the 3.5 day slow period and the succeeding 2.4 day period of intermediate apparent motion.
7. The complex short-period variations in motion such as those seen in Figure 5 are subject to the same ambiguity of interpretation as to whether they represent actual variations in basal sliding or are artifacts due to irregular small hang-ups of the stake on the base of the ice. On the other hand, the longer-period variations (Table 1) that took place outside the time window of large slowdown(s) (J.D. 353-360) appear to be real variations in sliding, not attributable to stake hang-up. The progressive slight increase in sliding s.1. (Table 1) suggests that during the course of the experiment the stake worked its way downward in a shear zone in the sill, as it might do as a result of collisions with rock clasts protruding downward from the ice. According to this interpretation, when the sliding rate reached essentially the full motion of 1.18 ± 0.1 m d-1, at the end of the run, the stake reached the bottom of the till shear zone and there was no till deformation below this level.
Table 1. Slitting rates averaged over 2 4 days (omitting the interval JR 353-360)

8. Although the basal water-pressure values (Fig. 6) are somewhat problematical because of the calibration correction that had to be applied, as discussed in the last section, relative values in terms of pressure increase or decrease are probably indicated correctly. If so, the record indicates a 2 day period of sharply and substantially decreased pressure during J.D. 350.5-352.5. This pressure event comes immediately before the 3.5 day period of slow apparent sliding, which starts at J.D. 353.4. If this is a real slow-down in sliding, then the correlation in time with the pressure event may indicate a causal connection, the decrease in water pressure apparently triggering the slow-down. However, what we would expect to see in a causal relation would be something different; if the causal relation involves sediment deformation, then the slow period and the period of low water pressure should occur together; if it involves pressure-induced basal cavitation, the slow period could lag the low-pressure period but the onset of slow sliding should precede the termination of low pressure. It is therefore not clear that the correlation can be taken as an indication that there was a real slow-down in sliding. A different correlation between basal sliding variations and water-pressure variations was observed in Trapridge Glacier, Canada, by Reference Blake, Fischer and ClarkeBlake and others (1994, p.596). In that case, peaks in pressure followed peaks in sliding rate, which was interpreted in terms of a cause effect relation. In our case, little is known observationally about the cause of the pressure fluctuations such as those in Figure 6 (Reference Engelhardt and KambEngelhardt and Kamb, 1997, section 5).
9. The apparent sliding velocity of 2.0 m d-1 observed in borehole 89-5 by the non-electrical tethered stake must contain considerable error, because it considerably exceeds the surface motion of 1.2 m d-1, but it nevertheless suggests rapid basal sliding at a location about 10 km from borehole 95-1.
Conclusions
From the observations, it follows that basal sliding plays an important, apparently predominating role in the rapid motion of Ice Stream B near UpB. The measured basal sliding reported here is basal sliding sensu lato, which may include a contribution from shear deformation of till close to the sole — how close depending on details of how the tethered stake behaved in the experiment. The interpretive model of this behavior that we think is the correct one (Fig. 7) implies that only till shear taking place within about 3 cm of the sole can contribute to the measured sliding. Alternative models involve an increase of this figure from 3 cm to 10 cm or 25 cm. We prefer the 3 cm model (Fig. 7), because it ran account for the lack of tether pay-out during the first 10 hours of the experiment, which the other models cannot. The thickness of a possible basal till shear zone detectable from its contribution to basal sliding — 3 cm, 10 cm or 25 cm. depending on model is small compared to the 9m thickness of the till layer inferred from seismic observations (Reference Rooney, Blankenship, Alley and BentleyRooney and others, 1987, fig. 4, abscissa 4150 m). The predominance of measured basal sliding thus implies that the mechanism of rapid ice-stream motion, whether by basal sliding sensu stricto or till deformation, is concentrated at or near the top of the till instead of being spread more or less uniformly throughout the thickness of the till layer as is sometimes assumed in ice-stream models (e.g. Reference AlleyAlley, 1990; Reference KambKamb. 1991).
The extent of predominance of basal sliding depends on whether the slow apparent sliding motion (average 0.07m d-1) observed for 3.5 days out of the full run of 26 days (Fig. 4) actually represents slow basal sliding or is instead an artifact of the tethered stake getting hung up temporarily on the bottom of the sliding mass. If it represents slow sliding, the average sliding rate including the slow period is 69% of the total surface motion of 1.18 m d-1, and we are presented with the remarkable and perhaps dubious situation in which the basal motion appears to switch back and forth, on a time-scale of a few days, between strongly predominating basal sliding (75-100% of the total motion) and strongly predominating till deformation (c. 90"/., of the total). The occurrence of a 2 day period of much reduced basal water pressure immediately before the slow period may be a possible cause for a slow-down in sliding but the relative timing of cause and effect differ significantly from what would be expected.
We think it more likely, however, that the period of slow apparent sliding was caused by temporary hang-up of the tethered stake on the glacier sole, according to the interpretive model in Figure 7f. If so, the proper measure of the average sliding rate is 0.98 m d-1, 83% of the total ice-stream motion. The likelihood of this interpretation is strengthened by its ability to explain the period of, slow apparent sliding without the need to conclude that the ice-stream mechanism switches rather rapidly hack and forth between basal sliding and till deformation, which seems somewhat improbable.
Till deformation, calculated as total motion minus observed basal sliding, contributes on the average 0.36 m d-1 or 0.20 m d-1 to the ice-stream motion (31% or 17% of the total motion), depending on which interpretation is placed on the 3.5 days of apparent slow sliding as discussed above.
The indicated predominance of basal sliding rules out the attractively simple picture used in a number of ice-stream models, in which basal sliding is omitted (e.g. Reference AlleyAlley and others, 1989; Reference MacAyealMacAyeal, 1989, Reference MacAyeal1992; Reference KambKamb, 1991). This affects formulation of the basal boundary condition (relation between basal shear stress and basal flow velocity) and the longitudinal transport of till, including the continuity condition on sources and sinks of till. The boundary condition for basal sliding sensu stricto is bound to be very différent from that for distributed deformation of till, because the physical processes taking place in the two mechanisms are so different. On the other hand, if the basal sliding (sensu lato) consists mainly of deformation in a thin shear zone in the till immediately below the ice, then the process is not radically different from distributed deformation and the boundary condition may be similar. The modeling problem is made considerably more complicated if the basal motion switches back and forth between basal sliding and distributed till deformation.
The applicability of the above conclusions to the ice streams as a whole depends on how representative the tethered-stake observations in the single borehole 95-1 are of the motion occurring broadly over the base of the ice stream (s) and over extended lengths of time. This can be assessed only by more borehole observations.
Acknowledgements
We acknowledge the help of personnel of the U.S. Antarctic Program, including the U.S. National Science Foundation, A.S.A., the U.S. Navy and the New York Air National Guard, and particularly our team of field assistants. R. Bolsey and V. Nenow helped greatly in the design and construction of the tethered stake instrument and in the field work. The work was made possible by grant No. OPP-9319018 from the U.S. National Science Foundation.