1 Introduction
Message-passing is a common communication model for developing concurrent and distributed systems where concurrent computations communicate through the passing of messages via send and recv operations. With growing demand for robust concurrent programming support at the language level, many programming languages or frameworks, including Scala (Haller & Odersky, Reference Haller and Odersky2009), Erlang (Armstrong et al., Reference Armstrong, Virding, Wikstrom and Williams1996), Go (Gerrand, Reference Gerrand2010), Rust (Klabnik & Nichols, Reference Klabnik and Nichols2020), Racket (Rac, 2019), Android (And, 2020), and Concurrent ML (Reppy, Reference Reppy1991), have adopted this model, providing support for writing expressive (sometimes first-class) communication protocols.
In many applications, the desire to express priority over communication arises. The traditional approach to this is to give priority to threads (Mueller, Reference Mueller1993). In a shared memory model, where concurrent access is regulated by locks, this approach works well. The trivial application of priority to message-passing languages, however, fails when messages are not just simple primitive values but communication protocols themselves (i.e. first-class representations of communication primitives and combinators). These first-class entities allow threads to perform communication protocols on behalf of their communication partners – a common paradigm in Android applications. For example, consider a thread receiving a message carrying a protocol from another thread. It is unclear with which priority the passed protocol should be executed – should it be the priority of the sending thread, the priority of receiving thread, or a user-specified priority?
In message-passing models such as Concurrent ML (CML), threads communicate synchronously according to the protocols constructed from send and receive primitives and combinators. In CML, synchronizing on the communication protocol triggers the execution of the protocol. Importantly, CML provides selective communication, allowing for computations to pick nondeterministically between a set of available messages or block until a message arrives. As a result of nondeterministic selection, the programmer is unable to impose preference over communications. If the programmer wants to encode preference, more complicated protocols must be introduced, whereas adding priority to selective communication gives the programmer to ability to specify the order in which messages should be picked.
Adding priority to such a model is challenging. Consider a selective communication, where multiple potential messages are available, and one must be chosen. If the selective communication only looks at messages and not their blocked senders, a choosing thread may inadvertently pick a low priority thread to communicate with when there is a thread with higher priority waiting to be unblocked. Such a situation would lead to priority inversion. Since these communication primitives must therefore be priority-aware, a need arises for clear rules about how priorities should compose and be compared. Such rules should not put an undue burden on the programmer or complicate the expression of already complex communication protocols.
In this paper, we propose a tiered-priority scheme that defines prioritized messages as first-class citizens in a CML-like message-passing language. Our scheme introduces the core computation within a message, an action, as the prioritized entity. We provide a realization of our priority scheme called PrioCML, as a modification to Concurrent ML. To demonstrate the practicality of PrioCML, we evaluate its performance by extending an existing web server and X-windowing toolkit. The main contributions of this paper are:
-
1. We define a meaning for priority in a message-passing model with a tiered-priority scheme. To our knowledge, this is the first definition of priority in a message-passing context. Crucially, we allow the ability for threads of differing priorities to communicate and provide the ability to prioritize first-class communication protocols.
-
2. We present a new language PrioCML, which provides this tiered-priority scheme. PrioCML can express the semantics of polling, which cannot be modeled correctly in CML due to nondeterministic communication.
-
3. We formalize PrioCML using a novel approach to Concurrent ML semantics focusing on communication as the reduction of communication actions. We leverage this approach to express our tiered-priority scheme and prove several important properties, most notably, freedom from communication derived priority inversions.
-
4. We implement the language PrioCML and evaluate its performance on the buyer-seller protocol, Swerve web server, and the eXene windowing toolkit as well as microbenchmarks.
This paper extends our previous work of PrioCML (Chuang et al., Reference Chuang, Iraci, Ziarek, Morales and Orchard2021) by providing a formal semantics of PrioCML, a case study and discussion of the buyer-seller protocol, added implementation details, as well as the tiered-priority scheme.
2 Background
We realize our priority scheme in the context of Concurrent ML (CML), a language extension of Standard ML (Milner et al., Reference Milner, Tofte and Macqueen1997). CML enables programmers to express first-class synchronous message-passing protocols with the primitives shown in Figure 1. The core building blocks of protocols in CML are events and event combinators. The two communication base events are sendEvt and recvEvt. Both are defined over a channel, a conduit through which a message can be passed. Here sendEvt specifies putting a value into the channel, and recvEvt specifies extracting a value from the channel. It is important to note both sendEvt and recvEvt are the functions to construct events, and those events do not perform their specified actions until synchronized on using the sync primitive. Thus, the meaning of sending or receiving a value is the composition of synchronization, and an event – sync (sendEvt(c, v)) will place the value v on channel c and, sync (recvEvt(c)) will remove a value v from channel c. In CML, both sending and receiving are synchronous, and therefore, the execution of the protocol will block unless there is a matching action.
Fig. 1. Core CML primitives.
The expressive power of CML is derived from the ability to compose events using event combinators to construct first-class communication protocols. We consider two such event combinators: wrap and choose. The wrap combinator takes an event e1 and a post-synchronization function f and creates a new event e2. Note that the function f is a value of type ’a -> ’b. When the event e2 is synchronized on, the actions specified in the original event e1 are executed; then, the function f is applied to the result. Thus, the result of synchronizing on the event e2 is the result of the function f.
To allow the expression of complex communication protocols, CML supports selective communication. The event combinator choose takes a list of events and picks an event from this list to be synchronized on. For example, sync (choose([recvEvt(c1), sendEvt(c2, v2)])) will pick between recvEvt(c1) and sendEvt(c2, v2) and based on which event is chosen will execute the action specified by that event. The semantics of choice depends on whether any of the events in the input event list have a matching communication partner available. Simply put, choose picks an available event, if only one is available, or nondeterministically picks an event from the subset of available events out of the input list. For example, if some other thread in our system performed sync (sendEvt(c1, v1)), then choose will pick recvEvt(c1). However, if a third thread has executed recvEvt(c2), then choose will pick nondeterministically between recvEvt(c1) and sendEvt(c2, v2). If no events are available, then choose will block until one of the events becomes available. The always event (alwaysEvt) creates an event that is always available and returns the value it stores when synchronized on. Always events are useful for providing default behaviors within choice. Dually, the never event (neverEvt) creates an event that is never available. If part of a choice, it can never be selected, and if synchronized on directly, the synchronization will never complete. This is useful for providing general definitions of constructs using choice.
A key innovation in the development of CML was support for protocols as first-class entities. Specifically, this means a protocol, represented by an event, is a value and can itself be passed over a channel. Once an event has been constructed from base events and event combinators, it can be communicated to another participant. This is the motivation for the division of communication into two distinct parts: the creation of an event and the synchronization on that event. In CML, the first-class nature of events means these phases may happen a different number of times and on different threads. In CML programs, first-class events provide an elegant encoding of call-back like behaviors.
3 Motivation
The desire for priority naturally occurs anywhere we wish to encode preference. Consider the Buyer-Seller protocol, commonly used an example protocol in both distributed systems (Ezhilchelvan & Morgan, Reference Ezhilchelvan and Morgan2001) and session types work (Vallecillo et al., Reference Vallecillo, Vasconcelos and Ravara2006). The protocol is a model of the interactions between a used book seller and a buyer negotiating the price for a book. We consider the variant in which there are two buyers submitting competing bids on a book from the seller. The seller receives the offers one at a time and solicits another offer if the offer is rejected. The protocol progresses until a buyer places an offer that the seller accepts. We can implement this protocol in CML by giving each buyer a channel along which they can submit bids to the seller. The seller selects a bid using the CML choose primitive to nondeterministically select a pending offer. The synchronous nature of CML send means that a buyer may only submit one bid at a time; they are blocked from executing until the bid is chosen. The core of this protocol is shown in Figure 2. We use the CML wrap event combinator to attach a label to the bid indicating which buyer it was received from.
Fig. 2. The two buyer-seller protocol.
Observe the choose primitive is entirely responsible for picking which buyer gets a chance to submit a bid. Although we express no preference in this protocol, the semantics of choose in CML are nondeterministic. Thus, while we would like for both buyers to have equal opportunity to submit bids, CML provides no guarantee of this. Fundamentally, what we desire is notion of fairness in the choice between the buyers. We roughly expect that the nondeterministic selection grants both buyers equal chance to be chosen. If the selections each round are statistically independent however, one buyer may, by chance, be able to place a significantly larger number of offers. This is because the number of bids placed has no influence on the selection in the next round. If a buyer is unlucky, they may be passed over several rounds in a row. To combat this CML integrates a heuristic for preventing thread starvation. That heuristic will attempt to prevent one buyer from repeatedly being selected, but makes no guarantees. We examine the effectiveness of this heuristic in Section 6.2. With priority, we could encode a much stronger fairness property. If we could express a preference between the buyers based on number of previous bids, we could enforce a round-robin selection that would guarantee the buyers submit an equal number of bids. The addition of priority would allow the programmer to control the undesirable aspects of nondeterminism in the system.
Where to add priority in the language, however, is not immediately clear. In a message-passing system, we have two entities to consider: computations, as represented by threads, and communications, as represented by first-class events. In our example, the prioritized element is communication, not computation. If we directly applied a thread-based model of priority to the system, the priority of that communication would be tied to the thread that created it. To prioritize a communication alone, we could isolate a communication into a dedicated thread to separate its priority. While simple, this approach has a few major disadvantages. It requires an extra thread to be spawned and scheduled. This approach also is not easily composed, with a change of priority requiring the spawning of yet another thread. A bigger issue is that the introduction of the new thread would then pass the communication message to the spawned thread, and the original thread is then unblocked as the message is sent to the spawned thread. This breaks the guarantee that the sent value will have been received in the continuation of the send that the synchronous behavior of CML provides. When communication is the only method to order computations between threads, this is a major limitation on what can be expressed.
Instead, consider what happens if we attach priority directly to communication. In the case of CML, since communications are first-class entities, this would mean prioritizing events. Assume we extend our language with new forms of events, like sendEvtP and recvEvtP which take an additional parameter that specifies the priority as shown in following type signature
We can use these new primitives to realize a prioritized variant of the protocol as code shown in Figure 3. Each receive event is wrapped with a post-synchronization function that increases the priority of the other buyer. This means that the higher priority will go to the buyer that has submitted fewer bids. PrioCML choice will always pick the event with highest priority within a selection.
Fig. 3. The prioritized two buyer-seller protocol.
This need to express a preference when presented with nondeterminism occurs in many CML programs. Consider as another example a web server written in CML. For such a server, it is important to handle external events gracefully and without causing errors for clients. One such external event is a shutdown request. We want the server to terminate, but only once it has reached a consistent state and without prematurely breaking client connections. Conceptually, each component needs to be notified of the shutdown request and act accordingly. We can elegantly accomplish this by leveraging the first-class events of CML. If a server is encoded to accept new work via communication in its main processing loop, we can add in shutdown behavior by using selective communication. Specifically, we can pick between a shutdown notification and accepting new work. The component can either continue or begin the termination process. However, by introducing selective communication, we also introduce nondeterminism into our system. The consequence is that we have no guarantee that the server will process the shutdown event if it consistently has the option to accept new work. The solution is to again use priority to constrain the nondeterministic behavior. By attaching a higher priority to the shutdown event, we express our desire that given the option between accepting new work and termination, we would prefer termination.
While event priority allows us to express communication priority, we still desire a way to express the priority of the computations. In the case of our server, we may want to give a higher priority to serving clients over background tasks like logging. The issue here is not driven by communications between threads but rather competing for computation. As such, we need a system with both event (communication) and thread (computation) priority.
The introduction of priorities in computation presents several problems when integrated with synchronous message-passing. Considering the priorities of threads and events in isolation gives rise to priority inversion caused by communication. Priority inversion happens when communication patterns result in a low priority thread getting scheduled in place of a high-priority thread due to a communication choosing the low priority thread over the high-priority one. This arises because we have no guarantee that the communication priorities agree with the thread priorities. To see this effect, consider the CML program shown in code where we use
$T_P$
to annotate the thread priority as high, medium, or low priority.
The programmer is free to specify event priorities that contradict the priorities of threads. Therefore, to avoid priority inversion, we must make choose aware of thread priority. A naive approach is to force the thread priority onto events. That is, an event would have the priority equal to that of the thread that created it. We can realize this approach in this example by changing sendEvt and recvEvt to sendEvtP and recvEvtP with thread priorities as the arguments. At first glance, it seems to solve the problem that shows up in the example above. The choice in
$T_L$
now can pick recvEvtP(c1, LOW) as the matching sendEvtP(c1, v1, HIGH) comes from
$T_H$
. This approach effectively eliminates event priorities, reviving all of the above issues with a purely thread-based model.
The desirable solution is to combine the priorities of the thread and the event. In order to avoid priority inversion, the thread priority must take precedence. This scheme resolves the problem illustrated. To resolve choices between threads of the same priority, we allow the programmer to specify an event priority. This priority is considered after the priority of all threads involved. This allows the message in our shutdown example to properly take precedence over other messages from high-priority threads.
This scheme is nearly complete but is complicated by CML’s exposure to events as first-class entities. Specifically, events can be created within one thread and sent over a channel to another thread for synchronization. When that happens, applying the priority of the thread that created the event brings back the possibility of priority inversion. To see why, consider the example in code:
In this example,
$T_H$
sends a sendEvt over the channel c3 which will be received and synchronized on by
$T_M$
. It is to be noted that this sendEvt will be at the highest priority (which was inherited from its creator
$T_H$
) even though it is synchronized on by
$T_M$
.
$T_H$
then sends out a value v1 on channel c1.
$T_L$
has to choose between receiving the value on channel c1 or on channel c2. Since
$T_H$
and
$T_M$
are both of higher priority than
$T_L$
, they will both execute their communications before
$T_L$
does. Thus,
$T_L$
will have to make a choice between either unblocking
$T_M$
or
$T_H$
(by receiving on channel c2 or c1 respectively). Recall that the priority is determined by the thread that created the event and not by the thread that synchronizes it in the current scenario. Therefore, this choice will be nondeterministic; both communications are of the same priority as those created by the same thread.
$T_L$
might choose to receive on channel c2 and thus allow the medium priority thread
$T_M$
to run while the high-priority thread
$T_H$
is still blocked – a priority inversion.
The important observation to be made from this example is that priority, when inherited from a thread, should be from the thread that synchronizes on an event instead of the thread that creates the event. This matches our intuition about the root of priority inversion, as the synchronizing thread is the one that blocks, and priority inversion happens when the wrong threads remain blocked.
We have now reconciled the competing goals of user-defined event priority and inversion-preventing thread priority. In doing so, we arrive at a tiered-priority scheme. The priority given to threads takes precedence, as is necessary to prevent priority inversion. A communication’s thread priority inherits from the thread that synchronizes on the event, as was shown to be required. When there is a tie between thread priorities, the event priority is used to break it. We note that high-priority communications tend to come from higher priority computations. Thus, this approach is flexible enough to allow the expression of priority in real-world systems.
4 Semantics
We now provide a formal semantics of PrioCML. Prior semantic frameworks for CML (e.g. Reppy, Reference Reppy2007; Ziarek et al., Reference Ziarek, Sivaramakrishnan and Jagannathan2011) maintain per-channel message queues. This closely mirrors the main implementations of CML. To introduce priorities, we must assert that prioritization is correct with respect to all other potential communications. These properties can be expressed more clearly when the full set of possible communications is readily accessible. We thus model our semantics on actions, which encode the effect to be produced by an event and represent an in-flight message. These actions are kept in a single pool called the action collection. In Section 5, we show how these semantics can be realized as a modification to existing CML implementations with per-channel queues.
4.1 The PrioCML communication lifecycle
Before defining the semantics, we explore the process of PrioCML communication in the abstract, highlighting several key steps in the lifecycle. To express a communication, a programmer starts by creating an event. Themselves values, events represent a series of communication steps to be enacted and are constructed by taking a small set of base events, and applying event combinators to construct a desired communication. Base events in PrioCML come in one of four forms: send, receive, always, and never. Send and receive allow synchronous communication over channels. Always and never represent single ended communications that can either always succeed immediately or will block forever. While useful in defining generic event combinators, they will also play a crucial internal role in the given PrioCML semantics by capturing the state of inactive threads. Each base event has a matching constructor (sendEvtP, recvEvtP, alwaysEvt, and neverEvt). These can be freely combined using event combinators (e.g. choose, wrap) and passed along channels as first-class values.
Event values have the form
${\varepsilon}\left[ \, {q} \, \right]$
, where q is one of following action-generating primitive: sendAct, recvAct, alwaysAct, neverAct, chooseAct, and wrapAct. The event context
$\varepsilon$
does not contain any event information but represents that no further reduction of the action-generating primitives is possible until synchronization. This delineation is important as it means the actions are generated at synchronization time and thus inherit the thread priority of the synchronizing thread and not the thread which created the event value.
When it is time for the enclosed communication steps (protocol) to be enacted, the sync primitive is used to perform event synchronization. The action-generating primitive inside the event context is reduced to a set of actions. For each base event type, there is a corresponding action. These actions represent the effect of a potential communication. In the case of a choice event, there may be multiple actions generated as there may be multiple potential (but mutually exclusive) communications. As each synchronization has exactly one result, we conceptualize any synchronization as being a choice between all of the generated actions. Nested choices are effectively flattened, and base events interpreted as choices with one element. Each action carries a choice id, a tag which uniquely identifies the synchronization that created it. This is used to prevent multiple actions from a single synchronization from being enacted.
Upon synchronization, the new actions are added to the action collection, a pool of all actions active in the system. From this pool, communication is chosen by an oracle which implements the prioritization. If the oracle picks a communication that is an always action, the enclosed value is given to the corresponding thread to restart execution. A communication can also be a pair of send and receive actions. In this case, any competing actions from the same choices are removed, the value is passed to form two always actions (one with the passed value for the receiving end and one with a unit value for the sending end), and the always actions thrown back into the pool. The selection process is then repeated until an always action is chosen, thereby passing a value to a thread and unblocking it.
We note that synchronization serves as the context switching point. A thread stops execution upon synchronizing, and the thread corresponding to the selected action takes its place. A fundamental property of our system (4.23) is that the thread executing always has the highest possible priority. In our system, this property can only be invalidated upon a communication, which requires synchronization and thus gives the system an opportunity to context switch.
4.2 Semantic rules
The syntax of our formalism is given in Figure 4. We define a minimal call-by-value language with communication primitives. We use q to define communication event primitives, which must appear wrapped in an event context
${\varepsilon}\left[ \, {q} \, \right]$
. Such a context prevents the reduction of the inner event until synchronization, at which point the thread information is captured. Event contexts are never encoded by the programmer directly but instead generated by the event primitive expressions. The full set of expressions is represented by e and values by v.
Fig. 4. Core syntax.
Our program state is a triple of a currently executing thread
$\left(T\right)$
, a collection of suspended threads
$\left(\overline{T}\right)$
, and a collection of current actions
$\left(\overline{\alpha}\right)$
. A thread contains a thread id
$\left(t\right)$
coupled with a thread priority of High, Med, or Low, and a current expression in an evaluation context
${E}\left[ \, {\cdot} \, \right]$
. We assume thread ids to be opaque values supporting only equality. A program begins execution with a single thread containing the program as its expression and an empty thread collection and action collection.
Actions, representing the communication action to be effected by an event, can be one of four varieties: always
$\left( \mathbf{A}^{{\omega}, {f}, {p}}_{v} \right)$
, send
$\left( \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}} \right)$
, receive
$\left( \mathbf{R}^{{\omega}, {f}, {p}}_{c} \right)$
, or never
$\left( \mathbf{N}^{{\omega}, {f}, {p}} \right)$
. Actions carry a choice id
$\omega$
, a wrapping function f, a priority (containing both a thread priority
$p_t$
and a non-negative integer event priority
$p_e$
) p, and if appropriate a channel c or value v. The choice id
$\omega$
uniquely identifies the choice to which the action belongs and thus the corresponding thread. We note that channels in our semantics are not a structure that stores pending actions, but merely a tag used to determine if a send and receive action can be paired. Actions that are able to be enacted are represented by communications
$\left(\gamma\right)$
, which can consist of either a lone always action
$\left\langle \mathbf{A}^{{\omega}, {f}, {p}}_{v} \right\rangle$
or a matching pair of send and receive actions
$\left\langle \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right\rangle$
. We note that the channel must match between the send and receive actions in a communication. We refer to a set of actions (communications, threads) as an action collection
$\overline{\alpha}$
(communication collection
$\overline{\gamma}$
, thread collection
$\overline{T}$
), which is an element of the power set of actions (communications, threads).
Program steps are represented by state transitions
$\rightarrow$
. We define several auxiliary relations used in defining the program step. Selection
$\rightsquigarrow$
maps an action collection to the chosen action and an action collection containing all action still valid after that choice. We note that section is a relation, and any one of multiple valid choices may result from a given action collection. Action generation
$\hookrightarrow$
creates an action from an action primitive, a thread priority, and a choice id. Communication generation
$\Rightarrow_{\overline{\alpha}}$
is a relation between an action and all possible communications involving that action, parameterized by the set of available actions. We adopt the convention that when applied to a set of actions, the communication generation relation maps to the union of all sets resulting from the application of the relation to each element of the input set.
\begin{align*} \rightarrow &\in \textit{State} \rightarrow \textit{State} \\ \rightsquigarrow &\in \textit{ActionCollection} \rightarrow \textit{Comm} \times \textit{ActionCollection} \\ \hookrightarrow &\in \textit{Prim} \times \textit{ThreadPrio} \times \textit{ChoiceID} \rightarrow \textit{ActionCollection} \\ \Rightarrow_{\overline{\alpha}} &\in \textit{ActionCollection} \rightarrow 2^{\textit{Action}\,\times\textit{Comm}} \\ \Psi &\in \textit{CommCollection} \rightarrow \textit{Comm} \\ \le_{prio} &\in Comm \times Comm\end{align*}
Function application is defined in the rule App. Channel creation happens when a channel expression is evaluated (rule Chan), and a new channel id c is generated.
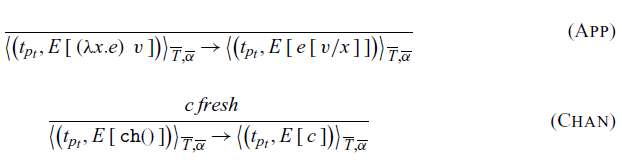
Threads are created through the spawn primitives with a user-specified priority. Spawn broken up in two cases, Spawn-NPreempt and Spawn-Preempt. These two rules cover the cases of spawning a thread with lower or higher priority, respectively. We distinguish here because we wish to maintain the invariant that the highest priority thread able to make progress is the one executing. If the thread we are spawning has lower (or equal) priority, we can continue executing the current thread. We add the newly spawned thread to the thread collection by blocking it on an always action
$\left(\mathbf{A}^{{\omega}, {\lambda x.x}, {p^\prime}}_{\texttt{unit}}\right)$
and adding that action to the action collection
$\left(\overline{\alpha}^\prime\right)$
. This preserves the invariant that all threads in the thread collection are blocked synchronizing on a choice (here, a choice of one action). If it is the case that the newly created thread has a higher priority than the one executing, we must switch to it immediately. To switch threads, we block the currently executing thread by synchronizing on an always action with the event priority equal to zero. We then set the new thread as the currently executing thread. In both cases, the expression that forms the body is the composition (represented by the function composition operator,
$\circ$
) of the always synchronization, the function e given to spawn, and a synchronization on a never event at thread completion. This approach avoids the complication of removing the threads from the collection and ensures that the thread will cease execution. As its name implies, a never action cannot be part of communication and thus will not be selected.
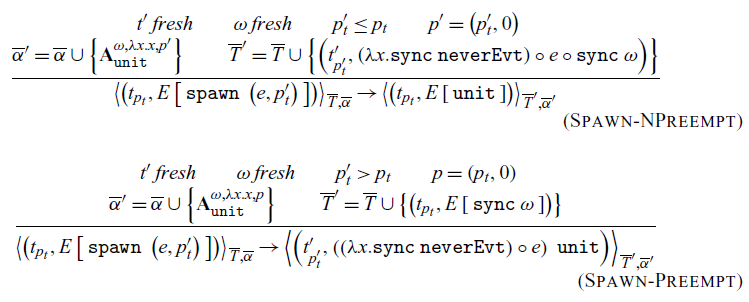
Following rules form the mechanism by which an event is evaluated. For each base action, there is a corresponding event primitive. Each event is reduced to an action-generating function inside an event context
$\varepsilon$
. Note that the action-generating function only carries the event priority and not the thread priority. This is because this reduction happens at event creation time and not event synchronization time. If we were to capture the thread priority at this point, it would allow for priority inversion as outlined in Section 3.
The rules ChoiceEvt and WrapEvt expand the event context
$\varepsilon$
, the new context will have chooseAct and wrapAct, respectively. Both chooseAct and wrapAct enclose their inner actions and then unpack it upon the synchronization. We also note that nested choices retain their nested structure at this stage (rule ChoiceEvt); for example, a choose event is in the list of another choose event. These are later collapsed in the rule ChoiceAct.
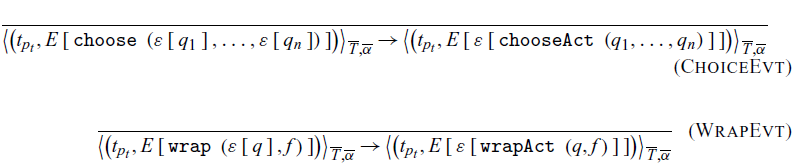
The action semantics deal with the process of synchronizing on an action. They are aided by an auxiliary relation, the action generation operator
$\hookrightarrow$
. In the simplest case, shown in the rule AlwaysAct, a single always action-generating function is transformed into the corresponding always action. Note that this rule is where the thread priority is incorporated into the action because this reduction happens at synchronization. Therefore, we capture the thread priority of the thread that will be blocked by this action, as is necessary for our desired properties to hold (see Theorem 4.23 and Lemma 4.22). The rules SendAct and RecvAct work similarly. In the more complex case of choice, handled by the rule ChoiceAct, we need to combine all of the actions produced by the events being combined, as a choice can result in multiple actions being produced. In the case of a nested choice operation, the rule applies recursively, taking the union of all generated actions and effectively flattening the choice. For rule WrapAct, the wrap operation also relies on the action set and maps each action in the set to an action with the function to wrap composed with the wrapping function f of each action.
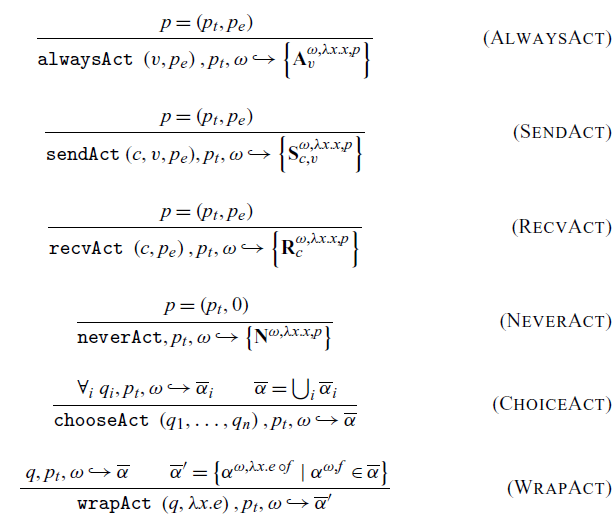
The actual synchronization is defined by the rule Sync. It generates a fresh choice id
$\omega$
, as each choice id conceptually represents a single synchronization operation and connects the synchronizing thread to the actions in the action collection. The action generation operator
$\hookrightarrow$
is then used to create the set of new actions
$\left(\overline{\alpha}^\prime\right)$
to be added to the action collection. This set of new actions is combined with the existing actions
$\left(\overline{\alpha}\right)$
to derive the intermediate action collection
$\overline{\alpha}^{\prime\prime}$
. This collection is then fed into the selection relation
$\rightsquigarrow$
to obtain the chosen communication and the new action collection
$\overline{\alpha}^{\prime\prime\prime}$
. The Sync rule requires that this communication be an always. If not, it must be a send-receive pair, and thus, the rule ReducePair can be applied repeatedly until an always communication is selected. The oracle is responsible for selecting a communication as described in Oracle. The choice id
$\omega^\prime$
from the chosen communication is used to select the correct thread out of the thread collection. Because the chosen communication may belong to the currently executing thread, which is not in the thread collection
$\overline{T}$
, we must search the set of all threads
$\overline{T}^{\prime\prime}$
. Upon finding the desired thread, we remove it from the set of all threads to obtain the new thread collection
$\overline{T}^{\prime\prime}$
. Lastly, we must continue executing the resumed thread by applying the wrapping function f to the value stored in the action.
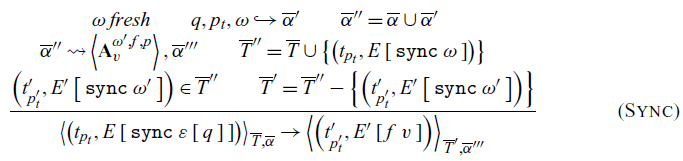
Now com the rules that govern the grouping of actions from the action collection into communications. A communication
$\gamma$
is either a single always action or a send and receive pair. The communication generating operator
$\Rightarrow_{\overline{\alpha}}$
is parameterized by
$\overline{\alpha}$
the action collection it is operating in. We define the operator over a single action in the rules CommAlways and CommPair, then adopt the convention that application of the operator to a set produces the image of that set, which is a set of all possible outputs of the operator from the elements of that input set. We note that in the rule CommPair we only operate on send actions and ignore receive actions. We do assert, however, that a compatible receive action is present in the set and generates one possible output (and thus communication) for each receive action. This choice is arbitrary, but either the sends or the receives must be ignored as inputs to prevent duplicate entries in the communication set. Further, the channel of the send and receive actions must match. Here the channel ids are treated as a tag which indicates which send and receive actions are allowed to be paired.
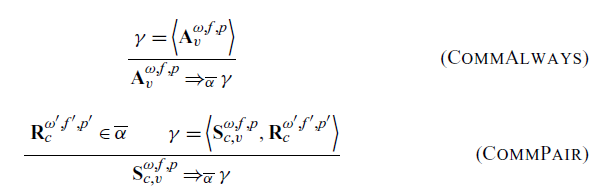
The remaining next rules define the selection relation
$\rightsquigarrow$
. This relation maps an action collection to a chosen communication and an action collection. This new action collection contains all of the actions that do not conflict with the chosen communication. This is critical in the case of choice, as it removes all unused actions generated during the choice.
In the simplest case, there is an always communication that is chosen by the oracle. This behavior is defined in the rule PickAlways. Here the communication collection
$\overline{\gamma}$
is generated from the action collection
$\overline{\alpha}$
, and the oracle
$\Psi$
is invoked. The action collection is then filtered to remove any actions with a choice id
$\omega^\prime$
matching the chosen action’s
$\omega$
. The always communication chosen by the oracle is returned, along with the filtered action collection
$\overline{\alpha}^\prime$
.
In the more complicated case, the oracle picks a send-receive communication. Then the rule PickPair applies. Similar to PickAlways, we generate the communications, pick one, and filter out all actions that conflict with either action in the communication. Note that PickPair results in a send-receive communication as the output of the selection relation
$\rightsquigarrow$
. However, in order to continue the execution of a thread, the Sync rule requires that right side of the relation be an always communication.
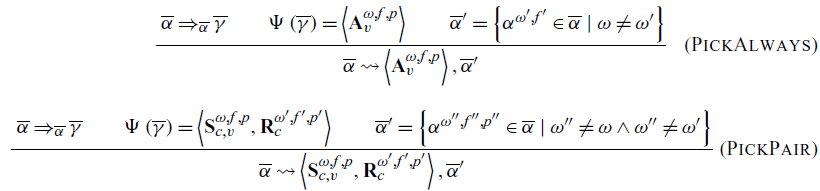
In order to output an always communication from the send-receive communication in rule PickPair, we apply the recursive rule ReducePair (rule at the bottom). If the selection over an action collection results in a send-receive pair as communication, we can reduce the send and receive to a pair of always actions and retry the selection. Conceptually, the send and receive actions are paired, and the values are passed through the channel. Each resultant always action carries the value to be returned: unit for the send and v for the receive. Those are added to the action collection, which is then used in the recursive usage of the selection relation
$\rightsquigarrow$
Rule ReducePair is what makes selection a relation and not a true functional map. This rule is necessary to create an invariant fundamental to the operation of these semantics: if there exists a member of the relation
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
, then there exists a member
$\overline{\alpha} \rightsquigarrow \gamma^\prime, \overline{\alpha}^{\prime}$
, where
$\gamma^\prime$
is an always communication. This stems from the ability to apply ReducePair if the relation can produce a send-receive pair. Note that
$\omega \neq \omega^\prime$
assert the two actions of the pair
$\gamma$
are from different threads since each choice id
$\omega$
and
$\omega^\prime$
is generated upon synchronization. Once this rule is applied, there is an always action in the collection that has the priority inherited from the original send-receive communication. We know this priority to be (at least tied as) the highest. As a consequence, any action collection that can produce a communication can produce an always communication, as required by Sync.
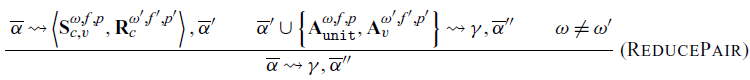
Conceptually, ReducePair encodes the act of communication in our system. The pairing of the send and receive and subsequent replacement by always actions is where values are passed from the sender to the receiver. We believe this view of communication as a reduction from a linked send and receive pair to two independent always actions provides a novel and useful way to conceptualize communication in message-passing systems. It provides a way to encode a number of properties, proofs of which can be found in Section 4.3.
The priority of communication is derived from the priority of its constituent actions. For an always communication, handled by the rule PrioAlways, this is simply the priority of the action. In the case of a send-receive pair, we need the max to be taken. We must take the max because this ensures that the priority of communication is always at least that of any of its actions. This invariant is crucial in our proofs of correctness. The rule PrioPair implements this behavior.
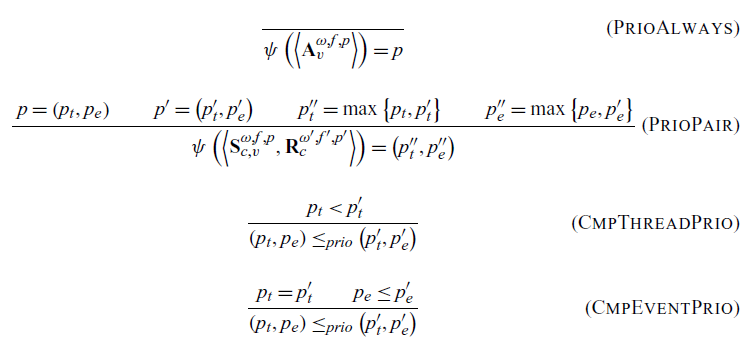
Priority is given a lexographic ordering. It is compared first by the thread component, as shown in the rule CmpThreadPrio. This ensures that a lower priority thread’s communication will never be chosen over a higher priority thread’s communication. If the thread priorities are the same, the rule CmpEventPrio says we then look at the event priorities.
The selection of a communication
$\gamma$
from the set of all possible communications
$\overline{\gamma}$
is done by an oracle
$\Psi$
. The oracle looks at all possible communications and (under these semantics) picks the one with the highest priority. The rule Oracle defines the oracle’s selection to have the highest priority of all possible communications. If there is a tie, we allow the oracle to choose nondeterministically.
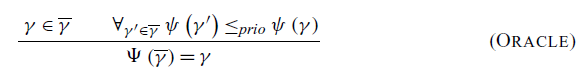
4.3 Proof of important properties
To provide some intuition about the operation of the above semantics, we now present proofs of several important properties of our semantic model.
4.3.1 Communication priority inversion
We start by showing that the selection operation fulfills the necessary properties used later to prove the lack of communication priority inversion and correctness of thread scheduling (Theorem 4.4). We say a selection causes a communication priority inversion (Definition 4.2) if the selection makes it impossible for an existing higher priority communication to be selected in the future. This happens when a selection eliminates (Definition 4.1) a communication, meaning it is no longer present in the communication collection derived from the resulting action collection. We note this is a relaxed definition of communication priority inversion that opens up opportunities for an oracle to make locally suboptimal decisions as long as they do not preclude making the optimal decision later. The oracle given in the semantics does not use this flexibility and will always choose the immediately highest priority communication.
Definition 4.1 (Elimination). A communication
$\gamma$
is eliminated by the selection
$\overline{\alpha} \rightsquigarrow \gamma^{\prime}, \overline{\alpha}^{\prime}$
, where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
and
$\overline{\alpha}^{\prime} \Rightarrow_{\overline{\alpha}} \overline{\gamma}^\prime$
, if
$\gamma \in \overline{\gamma}$
but
$\gamma \notin \overline{\gamma}^\prime$
.
Definition 4.2 (Selection Communication Priority Inversion). A selection
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
exhibits Communication Priority Inversion if it eliminates a communication
$\gamma^\prime$
, (
$\gamma^\prime \not= \gamma$
). where
$\psi \left( \gamma^\prime \right) \not \le_{prio} \psi\left( \gamma \right)$
Lemma 4.3 (Selection Priority). For a selection
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
, we have that for all
$\gamma^{\prime\prime} \in \overline{\gamma}$
,
$\psi\left(\gamma^{\prime\prime}\right) \le_{prio} \psi\left(\gamma\right)$
where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
.
Proof. By induction over the depth of the recursion. There are three rules by which a selection can be made: PickAlways, PickPair, and ReducePair.
In the case that the selection was by rules PickAlways or PickPair, we have that
$\Psi \left(\overline{\gamma}\right) = \gamma$
. By the definition of
$\Psi$
in the rule Oracle, we have that for all
$\gamma^{\prime\prime} \in \overline{\gamma}$
,
$\psi\left(\gamma^{\prime\prime}\right) \le_{prio} \psi\left(\gamma\right)$
.
If the selection was made by the recursive rule ReducePair, we have by the inductive hypothesis that our property holds for the antecedents
$\overline{\alpha} \rightsquigarrow \left< \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right>, \overline{\alpha}^{\prime\prime}$
and
$\overline{\alpha}^{\prime\prime} \cup \left\{ \mathbf{A}^{{\omega}, {f}, {p}}_{\texttt{unit}}, \mathbf{A}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{v} \right\} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
. Thus, we know that for all
$\gamma^{\prime\prime} \in \overline{\gamma}$
,
$\psi\left(\gamma^{\prime\prime}\right) \le_{prio} \psi\left( \left< \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right> \right)$
. By the rule PrioPair, we have that the priority of the selection
$\left< \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right>$
was both
$p \le_{prio} \psi\left( \left< \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right> \right)$
and
$p^\prime \le_{prio} \psi\left( \left< \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right> \right)$
. This is because the communication priority takes the max of each priority component and thus can be no less than either action priority. We note that the priorities of the generated always events are p and
$p^\prime$
, and that
$\left< \mathbf{A}^{{\omega}, {f}, {p}}_{\texttt{unit}} \right>$
and
$\left<\mathbf{A}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{v} \right>$
are members of
$\overline{\gamma}^{\prime\prime}$
, where
$\overline{\alpha}^{\prime\prime} \Rightarrow_{\overline{\alpha}^{\prime\prime}} \overline{\gamma}^ {\prime\prime}$
. Assume WLOG, the higher priority, and thus priority of the selection, to be p. Then again by our inductive hypothesis we obtain for all
$\gamma^{\prime\prime} \in \overline{\gamma}$
,
$\psi\left(\gamma^{\prime\prime}\right) \le_{prio} p \le_{prio} \psi\left(\gamma\right)$
. By transitivity, our property thus holds.
Theorem 4.4 (Selection Priority Inversion Freedom). No selection
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
exhibits Communication Priority Inversion under the given oracle
$\Psi$
.
Proof. Assume for sake of contradiction a selection
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^{\prime}$
exhibits Communication Priority Inversion by eliminating a communication
$\gamma^\prime$
. Then by the rules PickAlways and PickPair, we have that
$\Psi \left(\overline{\gamma}\right) = \gamma$
, where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
. By the definition of
$\Psi$
in the rule Oracle, we have that for all
$\gamma^{\prime\prime} \in \overline{\gamma}$
,
$\psi\left(\gamma^{\prime\prime}\right) \le_{prio} \psi\left(\gamma\right)$
. Because
$\gamma^\prime$
was eliminated, we know
$\gamma^{\prime} \in \overline{\gamma}$
. Thus
$\psi\left(\gamma^{\prime} \right) \le_{prio} \psi\left(\gamma\right)$
. This contradicts our assumption, as by our definition of Communication Priority Inversion,
$\psi \left( \gamma^\prime \right) \not \le_{prio} \psi\left( \gamma \right)$
.
4.3.2 Reduction relation
We can now show that any possible program transition does not produce a communication priority inversion (Theorem 4.8). Here we define our communication priority inversion over reductions and programs (Definition 4.7) analogously to our previous definition over selections (Definition 4.2). For the proof, we define an annotation to the reduction relation that encapsulates the communication used by that reduction (or
$\emptyset$
in the case that no communication occurs during the reduction). Leveraging this annotation, we can examine if the selection in the reduction eliminates a higher priority communication. Under the given oracle (and for any correct oracle), such elimination can never happen. Thus, a reduction, and by extension, a program trace, cannot exhibit communication priority inversion.
Definition 4.5 (Annotation). If
$S \rightarrow S^\prime$
by application of rule Sync where
$\overline{\alpha} \rightsquigarrow \gamma^{\prime}, \overline{\alpha}^{\prime}$
, then
$S \rightarrow_{\gamma^\prime} S^\prime$
. If
$S \rightarrow S^\prime$
by any other rule,
$S \rightarrow_\emptyset S^\prime$
.
Definition 4.6 (Reduction Elimination). A communication
$\gamma$
is eliminated by the reduction
$\left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}} \rightarrow \left\langle {T} \right\rangle_{\,{\overline{T}^\prime}, {\overline{\alpha}^\prime}}^\prime$
, where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
and
$\overline{\alpha}^{\prime} \Rightarrow_{\overline{\alpha}} \overline{\gamma}^\prime$
, if
$\gamma \in \overline{\gamma}$
but
$\gamma \notin \overline{\gamma}^\prime$
.
Definition 4.7 (Reduction Communication Priority Inversion). A reduction
$S \rightarrow_\gamma S^\prime$
exhibits Communication Priority Inversion if it eliminates a communication
$\gamma^\prime$
, (
$\gamma^\prime \not= \gamma$
) where
$\psi \left( \gamma^\prime \right) \not \le_{prio} \psi\left( \gamma \right)$
Theorem 4.8 (Priority Inversion Freedom). No reduction
$S \rightarrow S^\prime$
exhibits Communication Priority Inversion under the given oracle
$\Psi$
.
Proof. Assume for sake of contradiction a reduction
$S \rightarrow S^\prime$
exhibits Communication Priority Inversion by eliminating a communication
$\gamma^\prime$
. Note that by Definition 4.7, the reduction must be of the annotated form
$S \rightarrow_\gamma S^\prime$
and therefore been an application of the rule Sync. Let
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
and
$S^\prime = \left\langle {T} \right\rangle_{\,{\overline{T}^\prime}, {\overline{\alpha}^\prime}} ^\prime$
, and
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
and
$\overline{\alpha}^{\prime} \Rightarrow_ {\overline{\alpha}} \overline{\gamma}^\prime$
. By Definition 4.6, we have that
$\gamma^\prime \in \overline{\gamma}$
but
$\gamma^\prime \notin \overline{\gamma}^\prime$
. Thus, the selection performed,
$\overline{\alpha} \rightsquigarrow \gamma, \overline{\alpha}^ {\prime}$
, eliminates
$\gamma^\prime$
. by applying Definition 4.2, we have that the selection exhibits Communication Priority Inversion. This contradicts the prior result of Theorem 4.4. Hence, no such
$\gamma^\prime$
can exist, and therefore, no reduction exhibits Communication Priority Inversion.
Corollary 4.9 (Program Priority Inversion Freedom). Any program trace
$S \rightarrow^\ast S^\prime$
does not contain a Communication Priority Inversion.
4.3.3 Thread scheduling
Building on top of our prior results around communication priority inversion, we can now make the even stronger statement that under the given oracle, the highest priority thread that can make progress is the one executing. To do so, we must first define what it means for a thread to make progress. We say a thread is capable of making progress if it is ready (Definition 4.17). This happens when the thread is able to participate in a communication (see Definitions 4.13, 4.14, 4.15, and 4.16). We also observe that the semantics preserve an important invariant about the form of the threads waiting in the thread collection. They all must be synchronizing on a set of actions represented by a choice id (Lemma 4.19). This is integral to the cooperative threading model specified by the semantics because it implies that all threads are blocked from communicating. Even in cases where the communication is not meaningful, blocking can be encoded as synchronizing on an always action and termination as synchronizing on never.
These definitions provide the groundwork for inductively asserting that in any valid program state, the thread executing has higher priority than any ready thread in the collection (Theorem 4.23). The proof of this breaks down into three cases representing the three rules that modify the thread and action collections. The spawn cases are the simpler ones. We need two variants of the spawn rules to capture which thread should be blocked based on priority: the newly spawned thread or the spawning thread. Correctness stems from the fact that spawn always injects a synchronization to block the lower priority thread. The sync case is more complicated. At its core, the proof asserts that the priority of an action is linked to the thread that created it, and that thread is the one waiting on it. Note again that an action is generated from an event by the synchronizing thread, as was shown to be necessary in Section 3. Correctness of communication selection implies the correctness of action selection because thread and action priorities are linked, and this linkage is preserved through selection as well as the replacement of a communication pair with always actions. This in turn implies the correctness of thread selection. As a result, the thread currently executing is always the highest priority, showing our cooperative semantics are equivalent to traditional preemptive semantics that chooses only to preempt a thread for a higher priority one.
Definition 4.10 (Initial State). The initial state of a program is the state
$S_0 = \left\langle {\left( {0_{LOW}}, {e_0} \right)} \right\rangle_{\,{\emptyset}, {\emptyset}}$
.
Definition 4.11 (Reachable State). A reachable state S is a state such that
$S_0 \rightarrow^{\ast} S$
.
Definition 4.12 (Final State). A final state S is a state such that
$S = \left\langle {\left( {t_{p_{t}}}, {{E}\left[ \, {\texttt{sync}\ \omega}\, \right]} \right)} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \emptyset$
.
Definition 4.13 (Choice Participant). A choice id
$\omega$
is a participant in a communication
$\gamma$
iff the communication is of the form
$\gamma = \left\langle \mathbf{A}^{{\omega}, {f}, {p}}_{v} \right\rangle$
, or
$\gamma = \left\langle \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right\rangle$
, or
$\gamma = \left\langle \mathbf{S}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{{c}, {v}}, \mathbf{R}^{{\omega}, {f}, {p}}_{c} \right\rangle$
.
Definition 4.14 (Waiting). A thread T is waiting on choice id
$\omega$
iff
$T = \left( {t_{p_t}}, {{E}\left[ \, {\texttt{sync}\ \omega}\, \right]} \right)$
.
Definition 4.15 (Thread Participant). A thread T is a participant in a communication
$\gamma$
iff T is waiting on choice id
$\omega$
and
$\omega$
is a participant in
$\gamma$
.
Definition 4.16 (Available). A choice
$\omega$
is available in
$\overline{\alpha}$
iff there exists a communication
$\gamma \in \overline{\gamma}$
such that
$\omega$
is a participant in
$\gamma$
where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
.
Definition 4.17 (Ready). A thread
$T \in \overline{T}$
is ready in the state
$S = \left\langle {T^\prime} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
iff it is waiting on the choice id
$\omega$
and
$\omega$
is available in
$\overline{\alpha}$
.
Definition 4.18 (Blocked). A thread
$T \in \overline{T}$
is blocked in the state
$S = \left\langle {T^\prime} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
iff it is waiting on the choice id
$\omega$
and
$\omega$
is not available in
$\overline{\alpha}$
.
Lemma 4.19 (Thread Form). For any reachable state
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
all threads
$T^\prime$
in the thread collection
$\overline{T}$
are of the form
$T^\prime = \left( {t_{p_{t}}}, {{E}\left[ \, {\texttt{sync}\ \omega} \, \right]} \right)$
.
Proof. By induction over program steps
${S_n} \rightarrow {S_{n+1}}$
in
$S_0 \rightarrow^{\ast} S$
. At each step, we assume our desired property holds. By Definitions 4.11 and 4.10, all programs start in the initial state
$S_0 = \left\langle {\left( {0_{LOW}}, {e_0} \right)} \right\rangle_{\,{\emptyset}, {\emptyset}}$
. Since the initial thread collection is empty, the property is vacuously true in the initial state.
Proceed by case analysis over the rule applied in
${S_n} \rightarrow {S_{n+1}}$
. By our inductive hypothesis, the property holds over the thread collection in state
$S_n$
. Thus, we only consider rules that modify the thread collection.
Case Spawn-NPreempt: Here we have that the new thread collection
$\overline{T}^\prime$
is equal to the old one plus a new thread
$T^\prime = \left( {t^{\prime}_{p_{t}^{\prime}}}, { \left( \lambda x. \texttt{sync}\ \texttt{neverEvt} \right) \circ e \circ \texttt{sync}\ \omega } \right)$
. The new thread is indeed of the form
$T^\prime = \left( {t_{p_{t}}}, {{E}\left[ \, {\texttt{sync}\ \omega} \, \right]} \right)$
. Since all other threads in the collection are unchanged, by the inductive hypothesis, they too have the desired form. Hence, our property holds over thread collection
$\overline{T}^\prime$
and thus in state
$S_{n+1}$
.
Case Spawn-Preempt: By the same argument as in the previous case, except the new thread here is
$T^\prime = \left({t_{p_t}}, E [{\texttt{sync}\ \omega} ] \right) $
.
Case Sync: Here the new thread collection
$\overline{T}^\prime$
is a subset of an intermediate thread collection
$\overline{T}^{\prime\prime}$
, and the intermediate thread collection is the union of the current thread collection and the current thread state with the choice id applied. That state is of the form
$\left( {t_{p_{t}}}, {{E}\left[ \, { \texttt{sync}\ \omega} \, \right]} \right)$
. Since all other threads in the intermediate collection are unchanged from the current collection, by the inductive hypothesis, they too have the desired form. As all threads in the intermediate collection have the desired form, all threads in the new collection must too as
$\overline{T}^\prime \subset \overline{T}^{\prime\prime}$
. Hence, our property holds over thread collection
$\overline{T}^\prime$
and thus in state
$S_{n+1}$
.
Corollary 4.20 (Thread Status). For any reachable state
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha},}}$
all threads
$T^\prime$
in the thread collection
$\overline{T}$
are either ready or blocked.
Lemma 4.21 (Action Thread Priority). For any reachable state
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha},}}$
all threads
$T^\prime$
in the thread collection
$\overline{T}$
are waiting on a choice id
$\omega$
where for all actions with that choice id
$\alpha^{\omega, f, p} \in \overline{\alpha}$
, the thread priority of p matches the thread priority of
$T^\prime$
.
Proof. By induction over program steps
${S_n} \rightarrow {S_{n+1}}$
in
$S_0 \rightarrow^{\ast} S$
. At each step, we assume our desired property holds. By Definitions 4.11 and 4.10, all programs start in the initial state
$S_0 = \left\langle {\left( {0_{LOW}}, {e_0} \right)} \right\rangle_{\,{\emptyset}, {\emptyset}}$
. Since the initial thread collection is empty, the property is vacuously true in the initial state.
Since the property holds in
$S_n$
, we consider only rules that modify
$\overline{T}$
or
$\overline{\alpha}$
. By Lemma 4.19, all threads in the action collection are waiting on a choice id. Thus, we must only show that the priority of all actions matches the thread’s priority.
Case Sync: New actions can be generated by either the action generation operator
$\hookrightarrow$
or the communication selection operator
$\rightsquigarrow$
. Rules AlwaysAct, SendAct, RecvAct, NeverAct, ChoiceAct, and WrapAct collectively define the action generation operator
$\hookrightarrow$
. In all cases, the actions generated share both a thread priority and choice id with the synchronizing thread. Thus by our inductive hypothesis and the definition of action generation, we have that the property holds over the union
$\overline{\alpha}^{\prime\prime}$
. The only way for the communication selection operator
$\rightsquigarrow$
to introduce a new action is through the rule ReducePair. There the generated always actions share both a choice id and priority with their respective send or receive actions. Thus, the property is preserved.
Case Spawn-NPreempt: Here the only new action generated is the always action associated with the new thread. Trivially, we see that this action has thread priority that matches the new thread being added to the thread collection. Since the choice id is fresh and all other threads in the collection are unchanged, our property still holds.
Case Spawn-Preempt: Similar to the non-preemption case, the generated action is an always action associated with the thread being added to the collection. This time that thread is the preempted thread. Again, we see that this action has matching thread priority. As all other threads stay the same, again the property holds.
As all other rules do not modify either the thread collection or the action collection, our property holds in state
$S_{n+1}$
, and by induction in all reachable states.
Lemma 4.22 (Participant Priority). In any reachable state
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
, if thread
$T^\prime = \left( {t_{p_t}}, {e} \right) \in \overline{T}$
, is a participant in a communication
$\gamma \in \overline{\gamma}$
, where
$\overline{\alpha} \Rightarrow_{\overline{\alpha}} \overline{\gamma}$
, then
$\psi_t \left( \gamma \right) \ge p_t$
.
Proof. Here we have two cases:
$\gamma = \left\langle \mathbf{A}^{{\omega}, {f}, {p}}_{v} \right\rangle$
, or
$\gamma = \left\langle \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right\rangle$
.
Case
$\gamma = \left\langle \mathbf{A}^{{\omega}, {f}, {p}}_{v} \right\rangle$
: Here the communication involves only a single always action. Thus by Lemma 4.21, we have that the priority
$\psi_t \left( p \right) = p_t$
. Since by rule PrioAlways, the priority of an always communication matches that of its action, our desired property holds.
Case
$\gamma = \left\langle \mathbf{S}^{{\omega}, {f}, {p}}_{{c}, {v}}, \mathbf{R}^{{\omega^\prime}, {f^\prime}, {p^\prime}}_{c} \right\rangle$
: Here the communication involves two actions and we thus have two possibilities: one where
$T^\prime$
shares a choice id with send action and another where it shares a choice id with the receive action. By Lemma 4.21, the priority of the action will match that of the thread
$T^\prime$
. Without loss of generality, assume the thread is associated with the send action. Now we have two further options, either our send action has thread priority greater than or equal to the receive action, or it has a thread priority less than the receive action. If the thread priority is greater than or equal to, by rule PrioPair, the communication will have a thread priority equal to that of
$T^\prime$
. In the case that the thread priority is less than the receive action, the thread priority will be that of the receive action as the rule PrioPair takes the maximum of the thread priorities. In this case, the thread priority of the communication will be greater than that of
$T^\prime$
. In either case,
$\psi_t \left( \gamma \right) \ge p_t$
.
Theorem 4.23 (Thread Scheduling). For any reachable state
$S = \left\langle {T} \right\rangle_{\,{\overline{T}}, {\overline{\alpha}}}$
,
$T = \left( {t_{p_t}}, {e} \right)$
, all threads
$T^\prime = \left( {t^\prime_{p_t^\prime}}, {e^\prime} \right)$
in the thread collection
$\overline{T}$
have priority
$p_t^\prime \le_{prio} p_t$
if the thread
$T^\prime$
is ready in state S.
Proof. By induction over program steps
${S_n} \rightarrow {S_{n+1}}$
in
$S_0 \rightarrow^{\ast} S$
. At each step, we assume our desired property holds. By Definitions 4.11 and 4.10, all programs start in the initial state
$S_0 = \left\langle {\left( {0_{LOW}}, {e_0} \right)} \right\rangle_{\,{\emptyset}, {\emptyset}}$
. Since the initial thread collection is empty, the property is vacuously true in the initial state.
Since the property holds in
$S_n$
, we again consider only rules that modify
$\overline{T}$
or
$\overline{\alpha}$
.
Case Sync: By contradiction. Consider the state
$S_{n+1} = \dots$
. Assume for sake of contradiction that there exists a thread
$T^{\prime\prime} \in \overline{T}^{\prime}$
such that
$T^{\prime\prime}$
is ready and has priority
$p_t^{\prime\prime} > p_t^\prime$
. Then there must exist a communication
$\gamma^\prime \in \overline{\gamma}^\prime$
, where
$\overline{\alpha}^{\prime\prime\prime} \Rightarrow_{\overline{\alpha}^{\prime\prime\prime}} \overline{\gamma}^\prime$
, that makes
$T^{\prime\prime}$
available by Definition 4.17. By Lemma 4.22
$\psi_{t} \left( \gamma^\prime \right) \ge p_t^{\prime\prime} > p_t^\prime$
. We have that
$\psi_{t} \left( \gamma \right) = p_t^\prime$
by Lemma 4.22 and the fact that
$\gamma$
is an always communication. By the definition of
$\le_{prio}$
given in rule CmpThreadPrio, it must be the case that
$\psi \left( \gamma^\prime \right) \not\le_{prio} \psi \left(\gamma \right)$
, because
$\psi_t \left(\gamma^\prime \right) > \psi_t \left( \gamma \right)$
.
Now either
$\gamma^\prime \in \overline{\gamma}$
or
$\gamma^\prime \notin \overline{\gamma}$
, where
$\overline{\alpha}^{\prime\prime} \Rightarrow_{\overline{\alpha}^{\prime\prime}} \overline{\gamma}$
. In the case that
$\gamma^\prime \in \overline{\gamma}$
, our earlier statement
$\psi \left( \gamma^\prime \right) \not\le_{prio} \psi \left(\gamma\right)$
directly contradicts Lemma 4.3. If
$\gamma^\prime \notin \overline{\gamma}$
, then
$\gamma^\prime$
was produced by
$\overline{\alpha}^{\prime\prime} \rightsquigarrow \gamma, \overline{\alpha}^{\prime\prime\prime}$
. Hence, the rule ReducePair was applied, as only that rule can introduce new actions and thus communications. In the rule ReducePair, only always actions are produced, meaning the new communications (including
$\gamma^\prime$
) must be always communications. Since the priority of the generated always actions match that of the matched send and receive action respectively, it must be the case that there existed a send-receive communication
$\gamma^{\prime\prime} \in \overline{\gamma}$
where the either constituent send or receive action had the priority
$p^{\prime\prime} = \left( p_t^{\prime\prime}, p_e^{\prime\prime} \right)$
. The priority of a send-receive communication, by definition in rule PrioPair, is the maximum of the event and thread priorities, and is thus no less than the priority of either constituent action. Therefore,
$\psi \left(\gamma^\prime\right) \le_{prio} \psi \left(\gamma^{\prime\prime}\right)$
and so
$\left(\gamma^{\prime\prime}\right) \not\le_{prio} \psi \left(\gamma\right)$
, again contradicting Lemma 4.3.
Case Spawn-NPreempt: By the inductive hypothesis, thread
$T = \left({t_{p_t}}, E [{\texttt{spawn}\ \left(e, p_t^{\prime} \right)}] \right) $
must be no lower priority than all ready threads in
$\overline{T}$
. Since the action added to the action collection is an always action with a fresh choice id, no blocked threads in the thread collection may become ready. Thus, the only new ready thread in the thread collection is the one added here. This thread is ready because we add a corresponding always action to the action collection, but we assert that it has thread priority no higher than the priority of T. Thus, T must still have priority no lower than any ready thread in the new thread collection.
Case Spawn-Preempt: By the inductive hypothesis, thread
$T = \left({t_{p_t}}, E [{\texttt{spawn} \left(e, p_t^{\prime} \right)}] \right) $
must be no lower priority than all ready threads in
$\overline{T}$
. The newly spawned thread has priority greater than T and thus higher than all ready threads in the thread collection
$\overline{T}$
. Since the action added to the action collection is an always action with a fresh choice id, no blocked threads in the thread collection may become ready. Thus, again the only new ready thread in the thread collection is the one added here with priority
$p_t$
. Therefore, the newly spawned thread must have priority greater (and thus no less) than any ready thread in the new thread collection
$\overline{T}^\prime$
.
As all other rules (App, Chan, *Evt) do not modify either the thread collection or the action collection, our property holds in state
$S_{n+1}$
, and by induction in all reachable states.
5 Implementation
To demonstrate that our priority scheme is practically realizable, we have implemented it as an extension to the CML implementation in MLton, an open-source compiler for Standard ML. Our implementation of PrioCML consists of approximately 1400 LOC, wholly in ML. It implements the tiered-priority scheme outlined in semantics while preserving the properties.
5.1 Priority atop CML
To understand why priority at the CML language level is needed, we first consider a prioritized communication channel built from existing CML primitives as shown in Figure 5. Implementing communication using a prioritized channel requires two-step communication. We need one step to convey the event priority and another to effect the event’s communication. The prioritized channel itself is encoded as a server that accepts communications and figures out the appropriate pairings of sends and receives (in this case, based on priority).
Fig. 5. Encoding priority atop CML primitives.
The sender blocks, waiting to receive a notification from the server acting as the priority queue, while it waits for its message to be delivered by the priority queue to a matching receiver. Once the priority queue successfully sends the value to a receiver, it unblocks the sender by sending a message. The mechanism is nearly identical for a receiver, but since we need to return a value, we pass an event generating function to the channel. While the per-communication overhead is undesirable, this encoding captures the behavior of event priority for send and receive. On selective communication, however, this encoding becomes significantly more complicated. A two-stage communication pattern makes encoding the clean-up of events that are not selected during the choice challenging.
We also still lack the ability to extract the priority information from threads. Although we can send the thread priority from the synchronizing thread together with the event priority, but now the thread priority becomes the part of message. The consequence is that pchannel will need to receive the message to know the thread priority. Observe that in the loop function of pchannel, we synchronize on a choice between either the sendEvtp or recvEvtp event. Here, the choice is resolved by in the order the clients synchronized on the channel since CML does not use the thread priority to order the messages.
Recall that preventing priority inversions requires reasoning about the priority of both threads and events. Therefore, implementing priority requires deep visibility into the internals of message-passing. As shown above, we could gain this by building an additional structure on top of CML. However, to encompass the full richness of CML, including thread priority and arbitrary use of choice, we would need effectively to reimplement all of it. Instead, we opt to realize our priority mechanism as a series of slight modifications to the existing CML runtime.
5.2 Extensions to CML
The major changes made to CML are in the thread scheduler and channel structure. These changes are exposed through a set of new prioritized primitives, shown in Figure 6.
Fig. 6. PrioCML primitives.
We extend the thread scheduler to be a prioritized round-robin scheduler with three fixed thread priorities. While other work has explored finer-grained approaches to priority (Muller et al., Reference Muller, Acar and Harper2018), for simplicity, we use a small, fixed number of priority levels. We opted for three priority levels as that is enough to encode complex protocols such as earliest deadline first scheduling (Buttazzo, Reference Buttazzo2011). Our implementation could be extended to more priority levels if desired. The new primitive spawnP spawns a new thread with a user-specified thread priority: LOW, MED, or HIGH. Threads within the highest priority level are executed in a round-robin fashion until all are either blocked or have completed. A thread is considered blocked when it is waiting on communication. If all high-priority threads are blocked, then medium priority threads are run until either (1) a high-priority thread is unblocked or (2) all medium threads block or have completed. If there are no available high-priority threads or medium priority threads to execute, then low priority threads will be scheduled. This scheme guarantees that a thread will never be chosen to run unless there are no higher priority threads that can make progress.
Event priority is managed by three primitives: sendEvtP, recvEvtP, and changePrio. The eventPrio is a positive integer where a larger number implies higher priority. The two base event primitives sendEvt and recvEvt are replaced by their prioritized versions. These functions take in an event priority and tie that priority to the created events. The changePrio function allows the priority of an existing event to be changed. All other CML primitives exist in PrioCML. The primitive spawn creates a thread with LOW priority. The base event constructors are given default priority levels and reduce calls to the new prioritized primitives. The combinators continue to work unchanged. In this way, our system is fully backward compatible with existing CML programs.
5.3 Realizing tiered priority
The main challenges in implementing the semantics given in Section 4 are dealing with the thread scheduling and action collection. The CML runtime uses preemptive scheduling, in contrast with our formal semantics where scheduling is cooperative. To avoid priority inversion, we must preserve the invariant formalized in Theorem 4.23: the currently running thread must always have a priority equal to or higher than every ready thread. We achieve this by ensuring in the scheduler that a thread can be preempted only by a thread of equal or higher priority. This maintains the core thread scheduling property required by the semantics.
Care is needed to efficiently implement the selection process. The semantics operate over an action collection, and for every communication must evaluate every possible pair within the system. Implementing this approach directly would be prohibitively expensive, as it would require maintaining all available pairs across the whole system in a global shared set. We thus instead localize the decisions by leveraging a more traditional channel structure. While channels in the formal semantics are merely tags, in our implementation, as in CML, they are backed by a queue at runtime.
In our implementation, action values fulfill roughly the same role as base events in CML. Since the channel of an action can never change, we can store all actions in their associated channel. In the semantics, the action collection contains all actions on which threads are currently blocked. We obtain the same behavior more efficiently by instead keeping the actions segmented by channel. Observe that any communication pair chosen by the oracle must involve the running thread. Because the action collection starts empty and each synchronization results in at most one communication, there can be no send-recv communication pairs waiting in the action collection before a synchronization. Thus, the oracles selection must be a communication pair involving an action generated by the synchronization of the currently running thread if one is available, or a context switch to another thread (via an always action) if not. As a result, we know any communication pair must come from within the channels of the actions from the current synchronization. This allows us to reduce the search for a pair from the entire global action collection to only the pairs in the channels which are synchronized on by the running thread.
The challenge now is to pick the communication that complies with the decision of the oracle. When a running thread synchronizes on a set of events, a set of candidate communication pairs is generated by pairing the corresponding action from the channels of the synchronized actions. In the case of a single send or receive event being synchronized, the candidates are all from the same channel. In the more complicated case of synchronizing on multiple actions with choose, the candidates may come from different channels. Note that synchronization on an always event is a special case where the candidate communication is an always communication and not a pair. Similarly, never events result in no candidate communications. From the observation above, we know that the oracles chosen communication is one of these candidates, or a context switch to another thread if no candidates exist. As a result, the highest priority communication among the candidates must be the oracle’s chosen communication.
To find this communication when an event is synchronized, we leverage the channel structure. To see how this is done, first consider the event matching mechanism in unmodified CML (Reppy, Reference Reppy2007). When an event is synchronized, the corresponding action is placed in a queue over the channel it uses. If there is a match already in the channel queue, the actions are paired and removed. In the case of choice, all potential actions are enqueued. Each carries a reference to a shared flag that indicates if the choice is still valid. Once the first action in a given a choice is paired, the flag is set to invalid. If upon attempting a match, the action has its flag set to invalid, it is removed, and the following action in the queue is considered. This lazy cleaning of the channel queues amortizes the cost of removal.
To evaluate the decision of the PrioCML oracle, we must look at the entire set of actions generated at synchronization. When a running thread synchronizes directly on a send or receive event, there is only one generated action and thus the candidate communications are all from the same channel. We consider every possible pairing within this channel and take the communication with the highest priority. The more general approach is required when a thread synchronizes on a choice event. Here multiple actions may be generated and thus multiple channels may need to be examined. As in the semantics, we treat always actions as generating a communication with the priority of the always action and ignore never actions. When multiple channels are involved, PrioCML generates a set of candidate communications for each channel used by a generated action. The highest priority candidate from each channel is then compared to find the highest priority of all. We rely on the associativity of the max priority operation to avoid realizing the entire set of candidate communications explicitly.
We now give an example to show how the decision is made in the implementation of PrioCML. Note that we use the subscript on the thread to denote the thread priority.
In this example, we have four pairs of communication pairs. There are two candidate pairs on the channel c1 and the other two pairs on the channel c2. First we pick best pairs from c1 and c2 respectively. In channelc1, we pick the candidate pair between thread T2 and T5 as the best pair from channel c1 due to this pair has a higher event priority. On the channel c2, we pick the candidate pair between thread T3 and T5 since T3 has a higher thread priority than T4. Then, we move on to pick the final pair from the best candidate pairs of channel c1 and c2. We compare the best candidate pairs according to the prioritization scheme from the oracle again to pick the final pair in the selective communication. As a result, the candidate pair between thread T2 and T5 is the chosen pair of the decision due to its thread priority is higher than the other candidate pair.
In our prioritized implementation, we split the channel queue into three queues: one for each thread priority level. Further, each queue is a priority queue ordered by event priority. Keeping those three priority queues separate allows us to access the queue for a given thread priority. We need to do this both for efficient insertion and for a correct implementation of pairing. We maintain these per-channel queues as highQ, medQ, and lowQ. We note that while, as in CML, these are kept separately for send and receive, it is impossible to have both pending send and receive actions over the same channel. We thus are always referring to the non-empty set of queues in our discussion.
As noted previously, the highest priority communication must always involve the current thread. Consider the case where the current thread is communicating on a channel c. Our system looks first at the thread priority. If there is a thread blocked on channel c of higher thread priority, we must pair it with the blocked thread of highest priority. If the current thread has a priority higher than (or equal to) all blocked threads, under our semantics, the possible communications will all have a thread priority equal to the current thread. Thus, we consider them tied for thread priority and pick by highest event priority among all possible communications.
We implement this logic with the code given below, which shows how the highest priority communication is found for a given channel. We are given the thread priority, syncTp, of the current thread, and the event priority of the current action ep.
For each of the queues, we look at the highest (event) priority action within. The list ls contains, for each queue, the priority of a communication between the current thread and the action from that queue, along with a tag marking which queue that communication came from. Following the semantic rule PrioPair, we compute the priority of those potential communications by taking the maximum thread and event priorities. We use an option type and store NONE if a queue is empty. Note that because the number of thread priorities is fixed, the list ls is of constant length (three in our system). From the possible communications in ls, we then use the helper function pickPrio to pick the queue with the highest priority communication. We return both the priority (useful when handling selective communication) and identify the queue involved.
Choice is handled similarly to how it was handled before priority. Again, lists are cleared lazily to amortize the costs of removal. The major overhead our scheme introduces is that inserting an action into a channel now requires additional effort to keep the queues in order. For a choice, this overhead must be dealt with for each possible communication path. The impacts of this are measurable but minor, as discussed in Section 6.1.
5.4 Polling
Polling, a common paradigm in concurrent programming, is fundamentally the ability to do a non-blocking query on an event. The primitives of CML (Figure 1 from Section 2) do not provide the ability to express non-blocking synchronization. The only available synchronization operation is sync, which is blocking.
This problem is illustrated by Reppy in Concurrent Programming in ML (Reppy, Reference Reppy2007). At first glance, the always event primitive could provide a non-blocking construction. This event is constructed with a value, and when synchronized, it immediately yields the wrapped value. By selecting between always and recv events, the synchronization is guaranteed not to block. Although this approach reflects the non-blocking behavior of polling, it has a flaw, as explained by Reppy, would look as follows:
While it is true that this construction will never block, it may also ignore available communications on the channel. The choose operation in CML is nondeterministic and could choose the alwaysEvt branch, even if the recvEvt would not block. This problem led to the introduction of a dedicated polling primitive recvPoll in CML. While its use is generally discouraged, it is vital in some communications protocols outlined by Reppy.
In our implementation of the semantics, always events can be associated with an event priority. Thus, we can assign the always event to a lower event priority in PrioCML:
This correctly captures the polling behavior desired. Because of our guarantee that an event is always picked if one is available, the thread executing the choice will still never block. Therefore, under our prioritized implementation, the above polling example from Reppy works with the intended polling behavior.
6 Evaluation
To demonstrate that our implementation is practical, we have conducted a series of microbenchmarks to measure overheads as well as a case study in an example web server and GUI framework written wholly in CML.
We evaluate the feasibility of our implementation in two ways: microbenchmarks to measure overheads, and a series of case studies see how priority can be applied in practice. These experiments were run on MLton 20180207 and our implementation (which is derived from it). The system used for running the microbenchmaks and buyer-seller and eXene case studies has Intel i7-6820HQ quad-core processor with 16 GB of RAM and ran macOS 12. We note that MLton is a single-core implementation, so although it supports multiple threads, these are multiplex over a single OS thread. Due to a limitation on the number of concurrent sockets available in macOS, the Swerve benchmark was run on a Linux system with a Intel i7-1185G7 quad-core processor with 32 GB of RAM.
6.1 Microbenchmarks
We present microbenchmarks that exercise spawn, send-receive, and choice. In spawn and send-receive, we see constant overheads for each communication as shown in Figures 7 and 8. We note that the send-receive benchmark performs n total communications where n is the number of iterations, so the constant overhead leads to a steeper slope to the line. To benchmark choice, we build a lattice of selective communication. The threads are arranged in a
$n \times n$
cylindrical mesh. Each thread performs a selective communication between two input channels, one from each thread immediately above it. It then sends the resulting message on its output channel, connects to the two threads below it in the mesh. To trigger the chained selective communication, a single message is sent to one cell in the top row. The message is exchanged nondeterministically through the mesh until it is received by the bottom cell. To show the growth behavior of this benchmark, we scaled both the height and width, so for a run parameterized by n, there were
$n^2$
choice cells, of which the message would pass through n. From the results shown in Figure 9, we observe that the runtimes of both CML and PrioCML appear quadratic. Our implementation shows a cost higher by a constant factor and thus a steeper curve. We manually examined the Swerve and eXene codebase to confirm that nested choice does not occur in any selective communication. Thus, while our implementation does exhibit measurable slowdown on this synthetic benchmark, we do not expect real-world performance to be severely affected.
Fig. 7. Spawn.
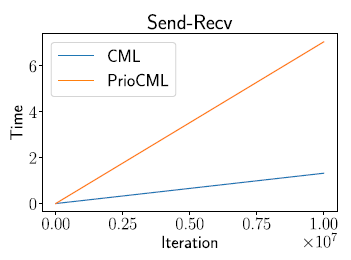
Fig. 8. Send-receive.
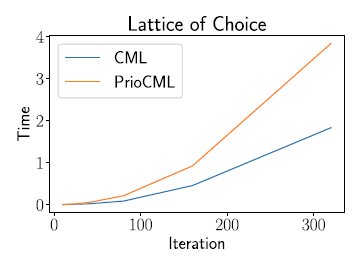
Fig. 9. Lattice of choice.
6.2 Case study: Prioritized buyer-seller
A key issue in some protocols is ensuring fairness between participants. We consider a protocol modeling the interactions between a bookseller and clients making offers to purchase a book. Introduced in the session types literature (Vallecillo et al., Reference Vallecillo, Vasconcelos and Ravara2006), this protocol is typically used to illustrate dyadic interactions that can be modeled with behavioral types. We explore an extension to this protocol that utilizes priority to enforce that the seller considers two competing buyers fairly. As introduced in Section 3, the buyer who missed a chance to bid will increase in priority. The higher event priority for this buyer means that bid will be chosen next by the seller.
We evaluate the performance on both MLton’s default CML implementation and PrioCML. The results shown in Figure 10 illustrate the difference between the number of offers placed by Buyer 1 and Buyer 2 as a function of the number of total offers made. To understand the behavior of the CML implementation, consider a system in which the buyer to interact with is determined by tossing a fair coin at each step. The difference between offers received from the buyers is then a one dimensional random walk process where the probabilities of a
$+1$
step and a
$-1$
step are both
$0.5$
. Such processes are common in many application domains and have well-known statistical properties (Weisstein n.d.). Specifically, we are interested in the expectation of the absolute difference: the average size of the imbalance. For large N, this is well approximated by
$E(| d_N |) = \sqrt{\frac{2 N}{\pi}}$
. Thus, after 5 million offers, we would expect the system that flips a fair coin to choose a buyer to exhibit an average imbalance of
$E(| d_{5 \times 10^6 } |) = \sqrt{\frac{2 \cdot 5 \times 10^6}{\pi}} \approx 1174$
offers. Thus while this system has a probabilistic idea of fairness, as the coin we flip is fair, the imbalance present would still be undesirably large. Ideally, we would want the difference to be at most 1 offer.
Fig. 10. Imbalance between buyers in Buyer-Seller.
Turning our attention to the performance of CML, we see that the imbalance observed after 5 million iterations is in fact 34 offers. While the output of a random walk is, as implied by the name, random, 34 is quite a bit smaller than the 1,174 expected from a fair coin flip. We take this as evidence the fairness heuristics in the CML implementation do perform quite well. Notably, as discussed in Section 7, CML implementations have traditionally had internal priority that is used heuristically to maintain fairness in nondeterministic choice. Such prioritization is considered an implementation detail in CML and not exposed to the programmer.
By exposing priority, we can allow the programmer to decide and encode what fairness means in their protocol. Here, we aim for a round-robin behavior, where the buyers take turns making offers. This has the desirable property that the imbalance in offers is capped at 1 offer. Looking at the results obtained in Figure 10, we see the imbalance stays very close to this ideal, but has occasional slight excursions to
$-1$
or 2. We attribute this behavior to preemptive thread scheduling. While our prioritization controls the nondeterminism present in communication actions, especially choice, we still have some nondeterminism present in thread preemption. This is because, unlike the cooperative semantics, the thread scheduling used in MLton’s CML implementation is preemptive. Thus, a buyer can occasionally be preempted before it is able to submit a new offer. If it fails to be scheduled soon enough, the other buyer may be able to submit two offers in a row because it is the only communication available. Importantly, our priority mechanism corrects for this behavior over time. The priority is based not on the last offer, but the total number of offers placed. Thus when the preempted buyer is able to place another offer it is given preference until it catches up to the other buyer. This protocol keeps the imbalance very small, even when presented with additional nondeterminism.
6.3 Case study: Termination in Swerve
To illustrate other uses of priority in message-passing programs, we take a look at a large CML project: the Swerve web server. Swerve is a modular web server written using CML with approximately 30,000 lines of code (Shipman, Reference Shipman2002). Written in the early 00s, Swerve was designed to showcase the utility of Concurrent ML in writing modular networked systems. We again note that the MLton CML runtime, and thus Swerve, is limited to utilizing a single CPU core. Even within single-core concurrent systems, the addition of priority to protocols can facilitate the easy addition of new features with minimal performance penalty.
As noted by Shipman, Swerve lacks a graceful shutdown mechanism. Currently, the shutdown of the web server is accomplished by sending a UNIX signal to terminate the process. This approach has several drawbacks. As the process is killed immediately, it does not have the opportunity to flush the asynchronous logging channel. This can lead to incomplete logs near the server shutdown. Additionally, clients being served at the time of server shutdown have their connections closed abruptly, without a chance for the server to finish a reply. This can lead to an error on the client-side or, in the case that the request was not idempotent, an inconsistent, or partially updated state server-side. Thus to cleanly exit the server, it is important to allow all currently running tasks to complete, including both flushing the log and handling connected clients. As Shipman (Reference Shipman2002) explains, this can be handled by rejecting all new clients and waiting for existing ones to finish before flushing the logs and exiting the process. We implement such a system in Swerve, the core of which is seen in Figure 12.
Fig. 12. Graceful shutdown in Swerve.
Here we select between the three possible actions in the main connection handling loop. We can accept an incoming connection over the channel acceptChan by invoking the function new_connect. Alternatively, we can handle a client disconnect event, sent as a message on the channel lchan via handle_msg. Lastly, we can receive a shutdown signal via the event shutdownEvt. This event is a receive event on a channel shared with the signal handler registered to the UNIX interrupt signal. Upon receipt of such a signal, the handler will send a message on that channel to indicate the server should begin shutdown. We leverage CML’s first-class events to encapsulate this mechanism and hide the implementation from the main loop. When the event shutdownEvt is chosen, we invoke the shutdown function, which stops accepting new connections, waits for all existing connections to close, flushes the log, then removes a lock file and exits.
While this change successfully resolves the possibility of broken connections and inconsistent server states, it still has a notable limitation. We have no guarantee of a timely shutdown. The original approach of killing the process via a signal is effectively instantaneous. However, because we want to complete the currently running server tasks, the server cannot shutdown immediately. We want to be sure that the server does not accept additional work after being told to shutdown. Under the existing CML semantics, the server is free to continue to accept new connections indefinitely after the shutdown event has become ready, provided a steady stream of new connections is presented. This is because there is no guarantee as to which event in a choice list is selected, only that it does not unnecessarily block. Since CML only allows safe interactions between threads via message-passing, we have no other way for the signal handler to alert the main loop that it should cease accepting new connections. Thus, under heavy load, the server could take on arbitrarily more work than needed to ensure a safe shutdown. We note that the MLton implementation of CML features an anti-starvation heuristic which in our testing was effective at preventing shutdown delays. This approach however is not a semantic guarantee. By adding priority, as shown in Figure 13, we obtain certainty that our shutdown will be effected timely.
Fig. 13. Prioritized shutdown in Swerve.
We verify the operation of this mechanism by measuring the number of clients that report broken connections at shutdown. With a proper shutdown mechanism, we would see no broken connections as the server would allow all to complete before termination. As seen in Figure 11, without the shutdown mechanism in place, clients can experience broken connections. When there are very few clients, the chances that any client is connected when the process terminates are low. As the number of clients increases, however, the odds of a broken connection do as well. By adding our shutdown mechanism, we prevent these broken connections. We emphasize that the introduction of priority means achieving a guarantee that the shutdown is correct is simple. The implementing code is short and concise because our mechanism integrates nicely with CML and retains its full composability. We note that event priorities are crucial to ensuring this timely shutdown. For example, consider when the signal handler was extended to pass on an additional type of signal, such as configuration reload. We would still want to ensure that the shutdown event takes precedence. Thus, we need to assign more granular priorities than those available based solely on the priority of the communicating thread.
Fig. 11. Swerve.
We observe that this protocol can be introduced to Swerve with minimal changes to the existing system. Importantly, this new functionality is not possible to correctly implement using existing CML primitives due to their inherent nondeterminism. While existing heuristics in CML provide an effective implementation of fairness, they make no promises of timely shutdown. By making the minor changes shown above, we obtain a semantic guarantee of priority that prevents the indefinite delay of the shutdown.
6.4 Case study: A GUI shutdown protocol
We now present an evaluation of response time measurement with a shutdown protocol in the context of eXene (Gansner & Reppy, Reference Gansner and Reppy1993), a GUI toolkit in CML. A typical eXene program contains widgets. To realize a graceful shutdown protocol, our eXene program needs to wait for all widgets to close upon receiving a shutdown request. Busy widgets tend to slow down the shutdown protocol as the protocol cannot continue while the widget is computing. Worse, the nondeterministic nature of choice can also have a negative impact on the latency of the shutdown protocol as widgets may overlook a shutdown request if other events are also available in the choice. We improve the response time, both shortening and stabilizing it (a reduction in mean and variance), by leveraging priority in the communication protocol. The priority here provides a clean mechanism to encode the preference of the shutdown events over regular processing events for widgets.
To fill up the work loads of each widget before triggering the shutdown protocol, we need to saturated the selective communication network between the GUI widgets. To do so, we leverage a synthetic network of widgets that computes Fibonacci numbers. Although the workload is synthetic, it highlights a complex interaction pattern between widgets that can easily be scaled as it creates a large number of selective communications. The number of communications needed to compute the n-th Fibonacci number grows exponentially with n. In order to compute Fibonacci numbers in our eXene widget network, each widget has a number corresponding to a position in the Fibonacci sequence. Upon a user click, the widget will calculate the corresponding Fibonacci number. By the definition of Fibonacci sequence, the widget for fib(n), excepting fib(0) and fib(1), needs to communicate with the other widgets responsible for computing
$fib(n-1)$
and
$fib(n-2)$
. Meanwhile, we need to encode the shutdown event so that widget has a chance to receive shutdown request. A widget can be implemented with CML code in Figure 16.
Fig. 16. Communication protocol of Fibonacci Widget.
Note that in Figure 16 we omit the case of sendEvt(fib_pre2_req, ()) for brevity. On the outermost select, the widget is waiting for either a compute request from out_ch_req or a shutdown request. Once it receives a compute request, it goes into the middle select. There it picks between the other widgets it needs to communicate with and the shutdown event. The code given shows the case where the widget for
$fib(n-1)$
is available. After we compute the result from
$fib(n-1)$
, it moves to
$fib(n-2)$
. Finally, it adds the results and sends the sum to the output channel in the innermost select, selecting another shutdown event. As for the shutdownEvt, every widget propagates the shutdown request to the widget of
$fib(n - 1)$
. Hence, the shutdown protocol in the Fibonacci network is a linear chain from the largest Fibonacci widget.
We encode priority in two places. First, the priority of the shutdown event is higher than other events. The use of priority in shutdown events ensures that the shutdown request will be chosen whenever it is available during a selection. Second, we give priority to send and recv on requesting and receiving the computation of the Fibonacci number. The message priority is higher when the index in the Fibonacci sequence is larger in the network. As a result, the widget with a larger number has a higher priority to request or receive computation. By giving these widgets preference, we boost the priority of shutdown protocol, as the linear chain is from largest to smallest widget.
The histograms of shutdown latency in CML and PrioCML are shown in Figures 14 and 15, respectively. We run each setting for 100 times and record the time needed to finish the shutdown protocol. We compute a large Fibonacci number to fill the network computation requests so that every widget is saturated with Fibonacci computation before requesting the shutdown protocol. The result shows that the average time spent on shutdown is improved by 26%, from 25.5 to 18.8 seconds. Also, it stabilizes the response time by reducing the standard deviation from 20.7 to 9.2 seconds.
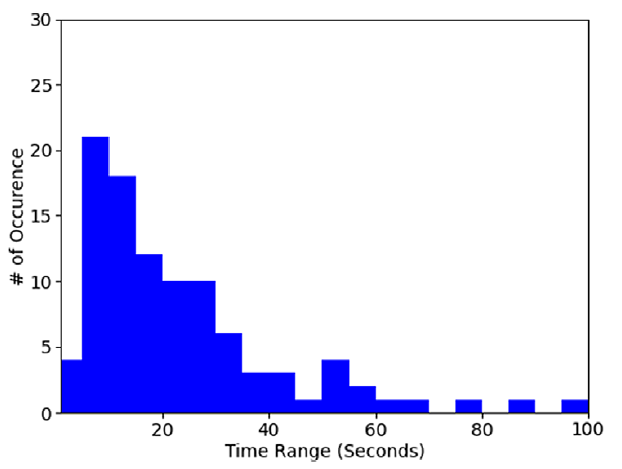
Fig. 14. CML.
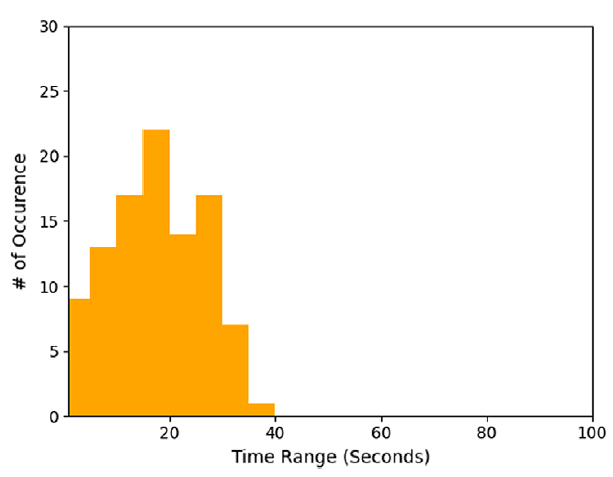
Fig. 15. PrioCML.
7 Related work
Priority in Multithreading:
Exploration into prioritized computation extends far back into research on multithreaded systems. Early work at Xerox on the Mesa (Lampson & Redell, Reference Lampson and Redell1980) programming language, and its successor project Cedar (Swinehart et al., Reference Swinehart, Zellweger and Hagmann1985), illustrated the utility of multiple priority levels in a multithreaded system. These systems exposed a fork-join model of concurrency, wherein the programmer would specify that any procedure shall be called by forking a new process in which to run it. The join operation then provides a synchronization point between the two threads and allows the computation to be obtained. This was implemented atop monitors, a form of mutual exclusion primitive. These systems did not consider communication as a first-class entity and only allowed it to use monitored objects.
First-Class Communication:
Concurrent ML introduced first-class synchronous communication as a language primitive (Reppy, Reference Reppy1991). Since then, there have been multiple incarnations of these primitives, both in languages other than ML (including Haskell Russell, Reference Russell2001; Chaudhuri, Reference Chaudhuri2009, Scheme Flatt & Findler, Reference Flatt and Findler2004, Go Gerrand, Reference Gerrand2010, and MPI Demaine, Reference Demaine1996). Others adopted CML primitives as the base for the parallel programming language Manticore (Fluet et al., Reference Fluet, Rainey, Reppy and Shaw2010). Other work has considered extending Concurrent ML with support for first-class asynchrony (Ziarek et al., Reference Ziarek, Sivaramakrishnan and Jagannathan2011). We believe our approach to priority would be useful in this context. It would, however, raise some questions regarding the relative priority of synchronous and asynchronous events, analogous to the aforementioned issues with always events. Another extension of interest would be transactional events (Donnelly & Fluet, Reference Donnelly and Fluet2008; Effinger-Dean et al., Reference Effinger-Dean, Kehrt and Grossman2008). The introduction of priority would be a natural fit as it provides a precise expression of how multiple concurrently executing transactions should be resolved. Crucially, this relies on an encoding of priority in events as a thread can be a participant in multiple competing transactions. Thus, the thread priority alone is not always enough to prioritize transactions.
Internal Use of Priority in CML Implementations:
As mentioned by Reppy (Reference Reppy2007) in describing the SML/NJ implementation of CML, a concept of prioritization has been previously considered in selective communication (Reppy, Reference Reppy2007). There, the principal goal is to maintain fairness and responsiveness. To achieve this goal, Reppy (Reference Reppy2007) proposes internally prioritizing events that have been frequently passed over in previous selective communications. We note that these priorities are never exposed to the programmer and exist only as a performance optimization in the runtime. Even if exposed to the user, this limited notion of priority only encompasses selective communication and ignores any consideration of the pairing communication. Our realization of priority and the associated tiered-priority scheme is significantly more powerful. This is both due to the exposure of priority to the programmer and our realization of priority to encompass information from both parties in communication when considering the priority of an event.
Priority in ML:
Recent work has looked at the introduction of priority to Standard ML (Muller et al., Reference Muller, Acar and Harper2018). To accomplish this, the system (Muller et al., Reference Muller, Acar and Harper2018) propose, PriML, “rejects programs in which a high priority may synchronize with a lower priority one.” Since all communication in CML is synchronous, in order for a high-priority thread to communicate with a lower priority thread, they must synchronize. This is exactly the interaction that is explicitly disallowed by PriML. A partial remedy to this problem would be to only allow asynchronous communication. This would then allow communication between lower and higher priority threads, but would still prevent any form of synchronization between such threads. Our approach makes the decision to allow the programmer the ability to express cross-priority synchronization.
8 Conclusion
This paper presents the design and implementation of PrioCML, an extension to Concurrent ML that introduces priority to synchronous messages passing. By leveraging a tiered-priority scheme that considers both thread priority and event priority, PrioCML avoids potential priority inversions. Our evaluation shows that this scheme can be realized to enable the adoption of priority with little effort and minimal performance penalties. We have formalized PrioCML and shown that PrioCML programs are free of communication induced priority inversion.
Conflicts of Interest
None.
Acknowledgements
This work is supported in part by National Science Foundation grants: CRI:1823230 and SHF:1749539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Appendix
Fig. A1. Derivation of a send and receive communication.
Fig. A2. Derivation of a send and receive communication (Cont.).
Open access
Discussions
No Discussions have been published for this article.