1 Introduction
Recursive types and bounded quantification are two prominent features in many modern programming languages, such as Java, C#, Scala, or TypeScript. Bounded quantification was introduced by Cardelli & Wegner (Reference Cardelli and Wegner1985) in the Fun language and has been widely studied (Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994; Pierce, Reference Pierce1994). Bounded quantification addresses the interaction between parametric polymorphism and subtyping, allowing polymorphic variables to have subtyping bounds. Recursive types are needed in practically all programming languages to model recursive data structures (such as lists or trees) or recursive object types in Object-Oriented Programming (OOP) languages to encode binary methods (Bruce et al., Reference Bruce, Cardelli, Castagna, Group, Leavens and Pierce1995). For adding recursive types to a language with subtyping, it is desirable to have recursive subtyping between recursive types. The first rules for recursive subtyping, due to Cardelli (Reference Cardelli1985), are the well-known Amber rules. Recursive subtyping has been studied in two different forms: equi-recursive subtyping (Amadio & Cardelli, Reference Amadio and Cardelli1993; Brandt & Henglein, Reference Brandt and Henglein1998; Gapeyev et al., Reference Gapeyev, Levin and Pierce2003) and iso-recursive subtyping (Bengtson et al., Reference Bengtson, Bhargavan, Fournet, Gordon and Maffeis2011; Ligatti et al., Reference Ligatti, Blackburn and Nachtigal2017; Zhou et al., Reference Zhou, Oliveira and Zhao2020, Reference Zhou, Oliveira and Fan2022). In equi-recursive subtyping, recursive types and their unfoldings are considered to be equal. In contrast, in iso-recursive subtyping they are only isomorphic, and explicit
![]() $\textsf{fold}/\textsf{unfold}$
operators are necessary to witness the isomorphism.
$\textsf{fold}/\textsf{unfold}$
operators are necessary to witness the isomorphism.
From the mid-80s and throughout the 90s, there was a lot of work on establishing the type-theoretic foundations for OOP. Both recursive subtyping and bounded quantification played a major part on this effort. The two features were perceived to be important to model objects in some forms of object encodings. At that time the key ideas around
![]() $F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994; Cardelli & Wegner, Reference Cardelli and Wegner1985), which is a polymorphic calculus with bounded quantification (but no recursive types), were reasonably well understood due to the early work on the Fun language by Cardelli & Wegner (Reference Cardelli and Wegner1985). Therefore,
$F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994; Cardelli & Wegner, Reference Cardelli and Wegner1985), which is a polymorphic calculus with bounded quantification (but no recursive types), were reasonably well understood due to the early work on the Fun language by Cardelli & Wegner (Reference Cardelli and Wegner1985). Therefore,
![]() $F_{\le}$
-like calculi were being used in foundational work on OOP. Some landmark papers on the foundations of OOP, which established important results such as the distinction between inheritance and subtyping (Cook et al., Reference Cook, Hill and Canning1989), F-bounded quantification (Canning et al., Reference Canning, Cook, Hill and Olthoff1989), or encodings of objects (Cook et al., Reference Cook, Hill and Canning1989; Abadi et al. Reference Abadi, Cardelli and Viswanathan1996; Bruce et al., Reference Bruce, Cardelli and Pierce1999), essentially assumed some
$F_{\le}$
-like calculi were being used in foundational work on OOP. Some landmark papers on the foundations of OOP, which established important results such as the distinction between inheritance and subtyping (Cook et al., Reference Cook, Hill and Canning1989), F-bounded quantification (Canning et al., Reference Canning, Cook, Hill and Olthoff1989), or encodings of objects (Cook et al., Reference Cook, Hill and Canning1989; Abadi et al. Reference Abadi, Cardelli and Viswanathan1996; Bruce et al., Reference Bruce, Cardelli and Pierce1999), essentially assumed some
![]() $F_{\le}$
variant with recursive types. Typically, recursive subtyping was supported via the Amber rules. However, extensions of
$F_{\le}$
variant with recursive types. Typically, recursive subtyping was supported via the Amber rules. However, extensions of
![]() $F_{\le}$
with recursive types had still not been developed and formally studied when many of those works were published.
$F_{\le}$
with recursive types had still not been developed and formally studied when many of those works were published.
After the first formalization of
![]() $F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992), Ghelli (Reference Ghelli1993) questioned this state-of-affairs, which implicitly assumed that the extension of
$F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992), Ghelli (Reference Ghelli1993) questioned this state-of-affairs, which implicitly assumed that the extension of
![]() $F_{\le}$
with recursive types was straightforward. He conducted the first formal study for such an extension and showed a wide range of negative results. Most importantly, he showed that equi-recursive types are not conservative over
$F_{\le}$
with recursive types was straightforward. He conducted the first formal study for such an extension and showed a wide range of negative results. Most importantly, he showed that equi-recursive types are not conservative over
![]() $\textrm{full}~F_{\le}$
. In other words, adding equi-recursive types to
$\textrm{full}~F_{\le}$
. In other words, adding equi-recursive types to
![]() $\textrm{full}~F_{\le}$
changes the expressive power of the subtyping relation, even when the types being compared do not involve any recursive types.
$\textrm{full}~F_{\le}$
changes the expressive power of the subtyping relation, even when the types being compared do not involve any recursive types.
The simple addition of equi-recursive types allows well-formed, but invalid subtyping statements in
![]() $F_{\le}$
to be valid in an extension with recursive types. Ghelli (Reference Ghelli1993) also shows that applying equi-recursive types to
$F_{\le}$
to be valid in an extension with recursive types. Ghelli (Reference Ghelli1993) also shows that applying equi-recursive types to
![]() $\textrm{full}~F_{\le}$
invalidates transitivity elimination: we cannot drop the transitivity rule without losing expressive power. In addition, while subtyping in
$\textrm{full}~F_{\le}$
invalidates transitivity elimination: we cannot drop the transitivity rule without losing expressive power. In addition, while subtyping in
![]() $\textrm{full}~F_{\le}$
is undecidable (Pierce, Reference Pierce1994), the change in expressive power reopened questions about the decidability or undecidability of the system.
$\textrm{full}~F_{\le}$
is undecidable (Pierce, Reference Pierce1994), the change in expressive power reopened questions about the decidability or undecidability of the system.
Even if we choose the weaker form of bounded quantification present in the Fun language and
![]() $\textrm{kernel}~F_{\le}$
, the natural extension of Amadio & Cardelli (Reference Amadio and Cardelli1993)’s algorithm to
$\textrm{kernel}~F_{\le}$
, the natural extension of Amadio & Cardelli (Reference Amadio and Cardelli1993)’s algorithm to
![]() $\textrm{kernel}~F_{\le}$
is incomplete (Colazzo & Ghelli, Reference Colazzo and Ghelli2005). In
$\textrm{kernel}~F_{\le}$
is incomplete (Colazzo & Ghelli, Reference Colazzo and Ghelli2005). In
![]() $\textrm{kernel}~F_{\le}$
, only universal quantifiers with equal bounds are allowed to be in a subtyping relation. This more restrictive formulation of bounded quantification is known to be decidable. However, complications still arise after adding equi-recursive types to
$\textrm{kernel}~F_{\le}$
, only universal quantifiers with equal bounds are allowed to be in a subtyping relation. This more restrictive formulation of bounded quantification is known to be decidable. However, complications still arise after adding equi-recursive types to
![]() $\textrm{kernel}~F_{\le}$
. Instead of Amadio & Cardelli (Reference Amadio and Cardelli1993)’s meet 2 times rules, Colazzo & Ghelli (Reference Colazzo and Ghelli2005) gave an alternative meet 3 times algorithm, accompanied by a very challenging correctness proof, showing that the subtyping relation is transitive and complete but did not prove conservativity. Based on an earlier draft from Colazzo & Ghelli (Reference Colazzo and Ghelli2005), Jeffrey (Reference Jeffrey2001) extended the system and proved it correct and complete. By transferring the polar bisimulations (Sangiorgi & Milner, Reference Sangiorgi and Milner1992) technique from concurrency theory, Jeffrey (Reference Jeffrey2001)’s system is more general than Colazzo & Ghelli’s, but it is only partially decidable. It is decidable for
$\textrm{kernel}~F_{\le}$
. Instead of Amadio & Cardelli (Reference Amadio and Cardelli1993)’s meet 2 times rules, Colazzo & Ghelli (Reference Colazzo and Ghelli2005) gave an alternative meet 3 times algorithm, accompanied by a very challenging correctness proof, showing that the subtyping relation is transitive and complete but did not prove conservativity. Based on an earlier draft from Colazzo & Ghelli (Reference Colazzo and Ghelli2005), Jeffrey (Reference Jeffrey2001) extended the system and proved it correct and complete. By transferring the polar bisimulations (Sangiorgi & Milner, Reference Sangiorgi and Milner1992) technique from concurrency theory, Jeffrey (Reference Jeffrey2001)’s system is more general than Colazzo & Ghelli’s, but it is only partially decidable. It is decidable for
![]() $\textrm{kernel}~F_{\le}$
with equi-recursive types, but for
$\textrm{kernel}~F_{\le}$
with equi-recursive types, but for
![]() $\textrm{full}~F_{\le}$
with equi-recursive types, only when the algorithm terminates it returns the correct answer, but it may not terminate. Furthermore, although being more powerful, Jeffrey (Reference Jeffrey2001)’s full system is not conservative over
$\textrm{full}~F_{\le}$
with equi-recursive types, only when the algorithm terminates it returns the correct answer, but it may not terminate. Furthermore, although being more powerful, Jeffrey (Reference Jeffrey2001)’s full system is not conservative over
![]() $\textrm{full}~F_{\le}$
either.
$\textrm{full}~F_{\le}$
either.
Table 1 summarizes the results of previous work on extending
![]() $F_{\le}$
with recursive types. Note that, in the table, the Type System row simply means whether the typing relation of the
$F_{\le}$
with recursive types. Note that, in the table, the Type System row simply means whether the typing relation of the
![]() $F_\le$
extension with recursive types has been studied/presented in the paper. For properties such as type soundness, decidability, or conservativity, there is a corresponding entry in the table, which states whether the property was proved or not. Modularity here means whether the original rules and definitions of
$F_\le$
extension with recursive types has been studied/presented in the paper. For properties such as type soundness, decidability, or conservativity, there is a corresponding entry in the table, which states whether the property was proved or not. Modularity here means whether the original rules and definitions of
![]() $F_\le$
are the same or they need to be modified.
$F_\le$
are the same or they need to be modified.
Table 1. Comparison among different works
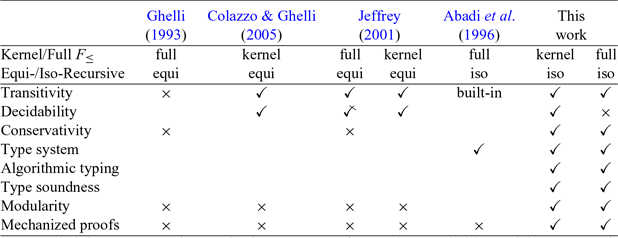
A
![]() $\times$
symbol denotes a negative result (the property or feature does not hold). A ✓ denotes a positive result, while
$\times$
symbol denotes a negative result (the property or feature does not hold). A ✓ denotes a positive result, while ![]() denotes a partial result (such as semi-decidability). Whitespace denotes that the property/feature has not been studied or it is unknown.
denotes a partial result (such as semi-decidability). Whitespace denotes that the property/feature has not been studied or it is unknown.
The proofs in all the four systems with equi-recursive types are complex because of the strong recursion, as can be seen from the literature. Adding equi-recursive subtyping requires major changes in existing definitions, rules, and proofs compared to
![]() $F_{\le}$
, making most of the existing metatheory on
$F_{\le}$
, making most of the existing metatheory on
![]() $F_{\le}$
not reusable. No prior work has proved the conservativity of
$F_{\le}$
not reusable. No prior work has proved the conservativity of
![]() $\textrm{kernel}~F_{\le}$
with equi-recursive types. This result is likely to be hard to prove because of the numerous non-modular changes in
$\textrm{kernel}~F_{\le}$
with equi-recursive types. This result is likely to be hard to prove because of the numerous non-modular changes in
![]() $F_{\le}$
induced by the introduction of equi-recursive subtyping. Furthermore, in those works, the full type systems are not provided.
$F_{\le}$
induced by the introduction of equi-recursive subtyping. Furthermore, in those works, the full type systems are not provided.
Motivated by the technical challenges and negative results posed by equi-recursive types, some researchers set their sights on iso-recursive types. In their work on object encodings, Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996) proposed the
![]() $F_{<:\mu}$
calculus, which supports bounded universal types, bounded existential types, and iso-recursive types via the Amber rules. However, reflexivity and transitivity are built in, so the system is not algorithmic. Furthermore, while they presented the typing, subtyping, and reduction rules, they have not proved any properties, including type soundness or the conservativity over
$F_{<:\mu}$
calculus, which supports bounded universal types, bounded existential types, and iso-recursive types via the Amber rules. However, reflexivity and transitivity are built in, so the system is not algorithmic. Furthermore, while they presented the typing, subtyping, and reduction rules, they have not proved any properties, including type soundness or the conservativity over
![]() $\textrm{full}~F_{\le}$
. One potential reason for the absence of technical results is that the iso-recursive Amber rules are hard to work with formally (Backes et al., Reference Backes, Hrițcu and Maffei2014; Ligatti et al., Reference Ligatti, Blackburn and Nachtigal2017; Zhou et al., Reference Zhou, Oliveira and Zhao2020, Reference Zhou, Oliveira and Fan2022): it is difficult to prove results such as transitivity or define sound and complete algorithmic formulations.
$\textrm{full}~F_{\le}$
. One potential reason for the absence of technical results is that the iso-recursive Amber rules are hard to work with formally (Backes et al., Reference Backes, Hrițcu and Maffei2014; Ligatti et al., Reference Ligatti, Blackburn and Nachtigal2017; Zhou et al., Reference Zhou, Oliveira and Zhao2020, Reference Zhou, Oliveira and Fan2022): it is difficult to prove results such as transitivity or define sound and complete algorithmic formulations.
This paper shows how to extend
![]() $F_{\le}$
with iso-recursive types in a calculus called
$F_{\le}$
with iso-recursive types in a calculus called
![]() $F_{\le}^{\mu}$
. In
$F_{\le}^{\mu}$
. In
![]() $F_{\le}^{\mu}$
, we add iso-recursive subtyping using the recently proposed nominal unfolding rules (Zhou et al., Reference Zhou, Oliveira and Fan2022). The nominal unfolding rules have been formally proved to be type sound and shown to have the same expressive power as the well-known iso-recursive Amber rules (Cardelli, Reference Cardelli1985). Moreover, the nominal unfolding rules address the difficulties of working formally with the (iso-recursive) Amber rules. With the nominal unfolding rules, proving transitivity and other properties is easy, also enabling developing algorithmic formulations of subtyping instead. Furthermore, a nice property of the nominal unfolding rules is that they are modular, allowing an existing calculus to be extended with recursive types without major impact on existing definitions and proofs. In other words, they allow reusing most existing metatheory and definitions that existed before the addition of iso-recursive types. Our work shows that the nominal unfolding rules proposed by Zhou et al. (Reference Zhou, Oliveira and Fan2022) can be integrated modularly into
$F_{\le}^{\mu}$
, we add iso-recursive subtyping using the recently proposed nominal unfolding rules (Zhou et al., Reference Zhou, Oliveira and Fan2022). The nominal unfolding rules have been formally proved to be type sound and shown to have the same expressive power as the well-known iso-recursive Amber rules (Cardelli, Reference Cardelli1985). Moreover, the nominal unfolding rules address the difficulties of working formally with the (iso-recursive) Amber rules. With the nominal unfolding rules, proving transitivity and other properties is easy, also enabling developing algorithmic formulations of subtyping instead. Furthermore, a nice property of the nominal unfolding rules is that they are modular, allowing an existing calculus to be extended with recursive types without major impact on existing definitions and proofs. In other words, they allow reusing most existing metatheory and definitions that existed before the addition of iso-recursive types. Our work shows that the nominal unfolding rules proposed by Zhou et al. (Reference Zhou, Oliveira and Fan2022) can be integrated modularly into
![]() $F_{\le}$
subtyping rules, while retaining desirable properties. In particular, we prove, for the first time, the conservativity of an extension of
$F_{\le}$
subtyping rules, while retaining desirable properties. In particular, we prove, for the first time, the conservativity of an extension of
![]() $F_{\le}$
with recursive types over the original
$F_{\le}$
with recursive types over the original
![]() $F_{\le}$
.
$F_{\le}$
.
In
![]() $F_{\le}^{\mu}$
, we use the so-called structural folding/unfolding rules for typing expressions with recursive types, inspired by the structural unfolding rule proposed by Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996). The structural rules add expressive power to the more conventional folding/unfolding rules in the literature, and they enable additional applications. In particular, we illustrate how the structural rules play an important role in modeling encodings of objects, as well as encodings of algebraic datatypes with subtyping.
$F_{\le}^{\mu}$
, we use the so-called structural folding/unfolding rules for typing expressions with recursive types, inspired by the structural unfolding rule proposed by Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996). The structural rules add expressive power to the more conventional folding/unfolding rules in the literature, and they enable additional applications. In particular, we illustrate how the structural rules play an important role in modeling encodings of objects, as well as encodings of algebraic datatypes with subtyping.
We study two variants of
![]() $F_{\le}^{\mu}$
. The first one has a generalization of the
$F_{\le}^{\mu}$
. The first one has a generalization of the
![]() $\textrm{kernel}~F_{\le}$
rule for bounded quantification that accepts equivalent rather than equal bounds. The second variant uses the rule of
$\textrm{kernel}~F_{\le}$
rule for bounded quantification that accepts equivalent rather than equal bounds. The second variant uses the rule of
![]() $\textrm{full}~F_{\le}$
for bounded quantification. We will refer to the first variant as kernel
$\textrm{full}~F_{\le}$
for bounded quantification. We will refer to the first variant as kernel
![]() $F_{\le}^{\mu}$
and to the second variant as full
$F_{\le}^{\mu}$
and to the second variant as full
![]() $F_{\le}^{\mu}$
. We present several results, including: type soundness; transitivity and (un)decidability of subtyping; the conservativity of
$F_{\le}^{\mu}$
. We present several results, including: type soundness; transitivity and (un)decidability of subtyping; the conservativity of
![]() $F_{\le}^{\mu}$
over
$F_{\le}^{\mu}$
over
![]() $F_\le$
; and a sound and complete algorithmic formulation of
$F_\le$
; and a sound and complete algorithmic formulation of
![]() $F_{\le}^{\mu}$
. The kernel
$F_{\le}^{\mu}$
. The kernel
![]() $F_{\le}^{\mu}$
variant is proved to have decidable subtyping, whereas the full
$F_{\le}^{\mu}$
variant is proved to have decidable subtyping, whereas the full
![]() $F_{\le}^{\mu}$
variant has undecidable subtyping. We also present an extension of
$F_{\le}^{\mu}$
variant has undecidable subtyping. We also present an extension of
![]() $F_{\le}^{\mu}$
, called
$F_{\le}^{\mu}$
, called
![]() $F_{\le\ge}^{\mu\wedge}$
, which has a bottom type, intersection types, and lower bounded quantification in addition to the conventional (upper) bounded quantification of
$F_{\le\ge}^{\mu\wedge}$
, which has a bottom type, intersection types, and lower bounded quantification in addition to the conventional (upper) bounded quantification of
![]() $F_\le$
. As we show, lower bounded quantification is useful to model the subtyping of algebraic datatypes. Intersection types are used to encode record types, similarly to how the Dependent Object Calculus (DOT) (Rompf & Amin, Reference Rompf and Amin2016) encodes object types. All the results in this paper have been formalized in the Coq theorem prover. In summary, the contributions of this paper are as follows:
$F_\le$
. As we show, lower bounded quantification is useful to model the subtyping of algebraic datatypes. Intersection types are used to encode record types, similarly to how the Dependent Object Calculus (DOT) (Rompf & Amin, Reference Rompf and Amin2016) encodes object types. All the results in this paper have been formalized in the Coq theorem prover. In summary, the contributions of this paper are as follows:
-
•
 $F_{\le}^{\mu}$
: extending
$F_{\le}^{\mu}$
: extending
 $F_{\le}$
with iso-recursive types. We have two variants of
$F_{\le}$
with iso-recursive types. We have two variants of
 $F_{\le}^{\mu}$
: kernel
$F_{\le}^{\mu}$
: kernel
 $F_{\le}^{\mu}$
as the extension of
$F_{\le}^{\mu}$
as the extension of
 $\textrm{kernel}~F_{\le}$
with iso-recursive subtyping, and full
$\textrm{kernel}~F_{\le}$
with iso-recursive subtyping, and full
 $F_{\le}^{\mu}$
as the extension of
$F_{\le}^{\mu}$
as the extension of
 $\textrm{full}~F_{\le}$
with iso-recursive subtyping. We prove several properties for
$\textrm{full}~F_{\le}$
with iso-recursive subtyping. We prove several properties for
 $F_{\le}^{\mu}$
, including: type soundness; transitivity of subtyping; decidability of subtyping of kernel
$F_{\le}^{\mu}$
, including: type soundness; transitivity of subtyping; decidability of subtyping of kernel
 $F_{\le}^{\mu}$
; undecidability of subtyping of full
$F_{\le}^{\mu}$
; undecidability of subtyping of full
 $F_{\le}^{\mu}$
; and the unfolding lemma, a key property to ensure type soundness.
$F_{\le}^{\mu}$
; and the unfolding lemma, a key property to ensure type soundness. -
• The conservativity of
 $F_{\le}^{\mu}$
over
$F_{\le}^{\mu}$
over
 $F_\le$
. Conservativity is an expected but nontrivial property that has eluded past work on the combination of bounded quantification and recursive types. We show that
$F_\le$
. Conservativity is an expected but nontrivial property that has eluded past work on the combination of bounded quantification and recursive types. We show that
 $F_{\le}^{\mu}$
is conservative over
$F_{\le}^{\mu}$
is conservative over
 $F_{\le}$
.
$F_{\le}$
. -
• Type soundness for the structural folding/unfolding rules. We present the first formal type soundness proof for the structural unfolding rule, and we also present a new structural folding rule, together with its type soundness.
-
• Decidability for kernel
 $F_{\le}^{\mu}$
. We show that kernel
$F_{\le}^{\mu}$
. We show that kernel
 $F_{\le}^{\mu}$
is decidable. The measure needed for decidability is nontrivial because there are significant differences in the measures for
$F_{\le}^{\mu}$
is decidable. The measure needed for decidability is nontrivial because there are significant differences in the measures for
 $\textrm{kernel}~F_{\le}$
and nominal unfoldings. We show how to develop a new measure that can account for both features at once. In addition, due to our generalization of the kernel rule to allow equivalent bounds, a key property for decidability is that equivalent types have equal sizes.
$\textrm{kernel}~F_{\le}$
and nominal unfoldings. We show how to develop a new measure that can account for both features at once. In addition, due to our generalization of the kernel rule to allow equivalent bounds, a key property for decidability is that equivalent types have equal sizes. -
• An extension of
 $F_{\le}^{\mu}$
with intersection types, both upper and lower bounded quantification: We present an extended calculus, called
$F_{\le}^{\mu}$
with intersection types, both upper and lower bounded quantification: We present an extended calculus, called
 $F_{\le\ge}^{\mu\wedge}$
, with a form of intersection types, both top and bottom types, and both upper and lower bounded quantification, and illustrate its applicability to encodings of datatypes with subtyping.
$F_{\le\ge}^{\mu\wedge}$
, with a form of intersection types, both top and bottom types, and both upper and lower bounded quantification, and illustrate its applicability to encodings of datatypes with subtyping. -
• Coq formalization: We have formalized all the calculi and proofs in this paper in Coq and made the formalization available online at https://github.com/juda/Recursive-Subtyping-for-All/tree/main/JFP.
Differences to the Conference Version
This article is a substantial enhancement of the conference paper (Zhou et al., Reference Zhou, Zhou and Oliveira2023). It introduces three major improvements over the original conference paper. The first improvement is the extension of our results to the
![]() $\textrm{full}~F_{\le}^{\mu}$
calculus, along with proofs demonstrating its type soundness and its conservativity over
$\textrm{full}~F_{\le}^{\mu}$
calculus, along with proofs demonstrating its type soundness and its conservativity over
![]() $F_{\le}$
. The initial conference version only addressed the addition of iso-recursive types into
$F_{\le}$
. The initial conference version only addressed the addition of iso-recursive types into
![]() $\textrm{kernel}~F_{\le}$
and left the extension to the full variant as an unresolved issue. The second improvement is a further generalization of the unfolding lemma that is capable of dealing with full
$\textrm{kernel}~F_{\le}$
and left the extension to the full variant as an unresolved issue. The second improvement is a further generalization of the unfolding lemma that is capable of dealing with full
![]() $F_{\le}$
, intersection types, and all the other extensions in this paper. The unfolding lemma is a central lemma in the metatheory of iso-recursive subtyping, and it is also where the main challenge in the metatheory lies. In the conference version, the generalized unfolding lemma was not able to deal with full
$F_{\le}$
, intersection types, and all the other extensions in this paper. The unfolding lemma is a central lemma in the metatheory of iso-recursive subtyping, and it is also where the main challenge in the metatheory lies. In the conference version, the generalized unfolding lemma was not able to deal with full
![]() $F_{\le}$
. Our new generalization addresses this issue, and it is shown to be general and applicable to a variety of extensions. The final improvement involves the combination of several important features within the system
$F_{\le}$
. Our new generalization addresses this issue, and it is shown to be general and applicable to a variety of extensions. The final improvement involves the combination of several important features within the system
![]() $F_{\le\ge}^{\mu\wedge}$
, and a much more detailed overview of
$F_{\le\ge}^{\mu\wedge}$
, and a much more detailed overview of
![]() $F_{\le\ge}^{\mu\wedge}$
. Unlike the conference version, which did not include intersection types, the updated
$F_{\le\ge}^{\mu\wedge}$
. Unlike the conference version, which did not include intersection types, the updated
![]() $F_{\le\ge}^{\mu\wedge}$
can model objects using structural folding/unfolding rules, intersection types, and single-field record types. This alternative way to model objects is inspired by, and aligns closely with, the encoding of objects in the DOT calculus.
$F_{\le\ge}^{\mu\wedge}$
can model objects using structural folding/unfolding rules, intersection types, and single-field record types. This alternative way to model objects is inspired by, and aligns closely with, the encoding of objects in the DOT calculus.
2 Overview
This section provides an overview of our work. We first briefly review basic concepts and some applications. Then we show our key ideas and results.
2.1 Bounded quantification and recursive subtyping
Bounded Quantification
Bounded quantification allows types to be abstracted by type variables with a subtyping constraint (or bound). The standard calculus with bounded quantification,
![]() $F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985; Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994), has two common variants when it comes to subtyping universal types. The
$F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985; Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994), has two common variants when it comes to subtyping universal types. The
![]() $\textrm{full}~F_{\le}$
variant (Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994) compares bounded quantifiers with the following rule:
$\textrm{full}~F_{\le}$
variant (Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994) compares bounded quantifiers with the following rule:

The most significant characteristic of
![]() $\textrm{full}~F_{\le}$
is that it allows two bounded quantifiers to be contravariant on their bound types
$\textrm{full}~F_{\le}$
is that it allows two bounded quantifiers to be contravariant on their bound types
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_2$
when being compared. However, the rich expressive power of
$A_2$
when being compared. However, the rich expressive power of
![]() $\textrm{full}~F_{\le}$
results in an undecidable subtyping relation (Pierce, Reference Pierce1994), which is undesirable. In addition, as Ghelli (Reference Ghelli1993) demonstrates, the S-fullall may even prevent conservative extensions of
$\textrm{full}~F_{\le}$
results in an undecidable subtyping relation (Pierce, Reference Pierce1994), which is undesirable. In addition, as Ghelli (Reference Ghelli1993) demonstrates, the S-fullall may even prevent conservative extensions of
![]() $F_{\le}$
in the presence of additional features.
$F_{\le}$
in the presence of additional features.
There are several ways to restrict bounded quantification to a fragment with decidable subtyping, such as removing top types, or assuming no bounds when comparing type abstraction bodies (Castagna & Pierce, Reference Castagna and Pierce1994). Among those the most widely used variant is the
![]() $\textrm{kernel}~F_{\le}$
calculus. In
$\textrm{kernel}~F_{\le}$
calculus. In
![]() $\textrm{kernel}~F_{\le}$
, bounded quantifiers can only be subtypes when their bound types are identical (Cardelli & Wegner, Reference Cardelli and Wegner1985), which is stated in the S-kernelall.
$\textrm{kernel}~F_{\le}$
, bounded quantifiers can only be subtypes when their bound types are identical (Cardelli & Wegner, Reference Cardelli and Wegner1985), which is stated in the S-kernelall.

In our paper, we will show how iso-recursive subtyping can be integrated with both kernel and full variants of
![]() $F_{\le}$
. However, for the kernel variant, differently from
$F_{\le}$
. However, for the kernel variant, differently from
![]() $\textrm{kernel}~F_{\le}$
, we will generalize the S-kernelall to a S-equivall that accepts equivalent bounds instead. The main motivation for using S-equivall is to enable more subtyping involving records. While typically
$\textrm{kernel}~F_{\le}$
, we will generalize the S-kernelall to a S-equivall that accepts equivalent bounds instead. The main motivation for using S-equivall is to enable more subtyping involving records. While typically
![]() $\textrm{kernel}~F_{\le}$
is presented without records, in this paper, we include records in the calculus and we wish to consider types such as
$\textrm{kernel}~F_{\le}$
is presented without records, in this paper, we include records in the calculus and we wish to consider types such as
![]() $\{x :\textsf{nat}, y : \textsf{nat}\}$
and
$\{x :\textsf{nat}, y : \textsf{nat}\}$
and
![]() $\{y : \textsf{nat}, x : \textsf{nat}\}$
, to be equivalent (despite being syntactically different). Note that, while in plain
$\{y : \textsf{nat}, x : \textsf{nat}\}$
, to be equivalent (despite being syntactically different). Note that, while in plain
![]() $F_{\le}$
the subtyping relation is antisymmetric (Baldan et al., Reference Baldan, Ghelli and Raffaetà1999) (i.e. if two types are equivalent then they must be equal), the addition of records breaks antisymmetry since there are equivalent types that are not equal. The S-equivall is more general than the kernel rule with identical bounds but retains decidability, as we shall see in Section 4.3.
$F_{\le}$
the subtyping relation is antisymmetric (Baldan et al., Reference Baldan, Ghelli and Raffaetà1999) (i.e. if two types are equivalent then they must be equal), the addition of records breaks antisymmetry since there are equivalent types that are not equal. The S-equivall is more general than the kernel rule with identical bounds but retains decidability, as we shall see in Section 4.3.
Recursive Types
Recursive types
![]() ${\mu{\alpha}}.{A}$
can be traced back to Morris (Reference Morris1968). There are two basic approaches to recursive types: equi-recursive types and iso-recursive types. The essential difference between them is how they consider the relationship between a recursive type
${\mu{\alpha}}.{A}$
can be traced back to Morris (Reference Morris1968). There are two basic approaches to recursive types: equi-recursive types and iso-recursive types. The essential difference between them is how they consider the relationship between a recursive type
![]() $\mu \alpha.~A$
and its unfolding
$\mu \alpha.~A$
and its unfolding
![]() $[\alpha \mapsto {\mu{\alpha}}.{A} ]~A$
. In equi-recursive types, a recursive type is equal to its unfolding. That is,
$[\alpha \mapsto {\mu{\alpha}}.{A} ]~A$
. In equi-recursive types, a recursive type is equal to its unfolding. That is,
![]() ${\mu{\alpha}}.{A} = [\alpha \mapsto {\mu{\alpha}}.{A}]~A$
. In other words, recursive types and their unfoldings are interchangeable in all contexts. Equi-recursive types also allow for more general equalities than unfoldings. For example, the types
${\mu{\alpha}}.{A} = [\alpha \mapsto {\mu{\alpha}}.{A}]~A$
. In other words, recursive types and their unfoldings are interchangeable in all contexts. Equi-recursive types also allow for more general equalities than unfoldings. For example, the types
![]() ${\mu{\alpha}}.{\textsf{int} \to \alpha}$
and
${\mu{\alpha}}.{\textsf{int} \to \alpha}$
and
![]() ${\mu{\alpha}}.{\textsf{int} \to \textsf{int} \to \alpha}$
are considered equivalent in the equi-recursive setting, since they have the same infinite unfolding (Amadio & Cardelli, Reference Amadio and Cardelli1993).
${\mu{\alpha}}.{\textsf{int} \to \textsf{int} \to \alpha}$
are considered equivalent in the equi-recursive setting, since they have the same infinite unfolding (Amadio & Cardelli, Reference Amadio and Cardelli1993).
In iso-recursive types, a recursive type and its one-step unfolding are not equal but only isomorphic. To convert between
![]() ${\mu{\alpha}}.{A}$
and
${\mu{\alpha}}.{A}$
and
![]() $[\alpha \mapsto {\mu{\alpha}}.{A}]~A$
, we need explicit
$[\alpha \mapsto {\mu{\alpha}}.{A}]~A$
, we need explicit
![]() $\textsf{unfold}$
and
$\textsf{unfold}$
and
![]() $\textsf{fold}$
operators. A fold expression constructs a recursive type, while an
$\textsf{fold}$
operators. A fold expression constructs a recursive type, while an
![]() $\textsf{unfold}$
expression opens a recursive type, as typing-fold and typing-unfold illustrate:
$\textsf{unfold}$
expression opens a recursive type, as typing-fold and typing-unfold illustrate:

Despite being less convenient, iso-recursive types are known to have the same expressive power as equi-recursive types (Abadi & Fiore, Reference Abadi and Fiore1996; Zhou et al., Reference Zhou, Wan and Oliveira2024). We will focus next on iso-recursive types.
Recursive Subtyping
Subtyping between recursive types has been studied for many years (Cardelli, Reference Cardelli1985; Amadio & Cardelli, Reference Amadio and Cardelli1993; Ligatti et al., Reference Ligatti, Blackburn and Nachtigal2017). The most widely used subtyping rules for recursive types are the Amber rules, first introduced in 1985 by Cardelli (Reference Cardelli1985) in a manuscript describing the Amber language (Cardelli, Reference Cardelli1985). The iso-recursive Amber rules deal with recursive subtyping with three rules: rule S-amber, S-assmp, and rule S-refl.

The Amber rules are simple, but their metatheory is troublesome. For example, transitivity is hard to prove (Bengtson et al., Reference Bengtson, Bhargavan, Fournet, Gordon and Maffeis2011; Zhou et al., Reference Zhou, Oliveira and Zhao2020, Reference Zhou, Oliveira and Fan2022). Furthermore, due to the reliance on the reflexivity rule (rule S-refl), the Amber rules are problematic for subtyping relations that are not antisymmetric (Ligatti et al., Reference Ligatti, Blackburn and Nachtigal2017). Recently, Zhou et al. (Reference Zhou, Oliveira and Zhao2020, Reference Zhou, Oliveira and Fan2022) proposed a new specification for iso-recursive subtyping and some equivalent algorithmic variants (Zhou & Oliveira, Reference Zhou and Oliveira2025). For this paper, we use one of those algorithmic variants, called the nominal unfolding rules (Zhou et al., Reference Zhou, Oliveira and Fan2022). The main reason for choosing the nominal unfolding rules is that they are easy to work with formally: indeed, Zhou et al. (Reference Zhou, Oliveira and Fan2022) have a full Coq development, including proofs of decidability, that we will reuse and extend.
Nominal Unfolding Rules
The nominal unfolding rules provide a formal mechanism for handling iso-recursive subtyping. These rules are designed to address the challenges posed by contravariant occurrences of recursive type variables. For recursive types, it is expected that if two recursive types
![]() ${\mu{\alpha}}.{A}$
and
${\mu{\alpha}}.{A}$
and
![]() ${\mu{\alpha}}.{B}$
are subtypes, then their unfolding
${\mu{\alpha}}.{B}$
are subtypes, then their unfolding
![]() $[\alpha \mapsto {\mu{\alpha}}.{A} ]~A$
and
$[\alpha \mapsto {\mu{\alpha}}.{A} ]~A$
and
![]() $[\alpha \mapsto {\mu{\alpha}}.{B} ]~B$
should also be subtypes. This property can be tricky to achieve with contravariant occurrences of recursive variables. The Amber rules deal with this issue by remembering pairs of recursive variables as subtyping assumptions, as can be seen in S-amber. In contrast, the nominal unfolding rules unfold the recursive body twice to ensure the correctness of the subtyping relation.
$[\alpha \mapsto {\mu{\alpha}}.{B} ]~B$
should also be subtypes. This property can be tricky to achieve with contravariant occurrences of recursive variables. The Amber rules deal with this issue by remembering pairs of recursive variables as subtyping assumptions, as can be seen in S-amber. In contrast, the nominal unfolding rules unfold the recursive body twice to ensure the correctness of the subtyping relation.
For example, consider the subtyping statement
![]() ${\mu{\alpha}}.{\alpha \to\textsf{nat}} \le {\mu{\alpha}}.{\alpha \to \top}$
. If we unfold the recursive types twice, we obtain:
${\mu{\alpha}}.{\alpha \to\textsf{nat}} \le {\mu{\alpha}}.{\alpha \to \top}$
. If we unfold the recursive types twice, we obtain:
This statement requires both
![]() $\textsf{nat} \le \top$
(which is true) and
$\textsf{nat} \le \top$
(which is true) and
![]() $\top \le \textsf{nat}$
(which is false), thus correctly rejecting the subtyping statement. Unfolding once would not expose the invalid
$\top \le \textsf{nat}$
(which is false), thus correctly rejecting the subtyping statement. Unfolding once would not expose the invalid
![]() $\top \le \textsf{nat}$
comparison.
$\top \le \textsf{nat}$
comparison.
The nominal unfolding rules simulate this double-unfolding process by replacing recursive types with labeled types (![]() ):
):

In rule S-nominal, every time two recursive types are compared, a fresh label
![]() $\color{red}{\alpha}$
is used to label the unfolded parts. Labeled types can only be compared to other labeled types with the same label, which ensures that they arise from the same recursive type, as shown in rule S-label. The bound type variable
$\color{red}{\alpha}$
is used to label the unfolded parts. Labeled types can only be compared to other labeled types with the same label, which ensures that they arise from the same recursive type, as shown in rule S-label. The bound type variable
![]() $\alpha$
in the recursive body becomes free variable after unfoldingFootnote
1
. For instance, to compare
$\alpha$
in the recursive body becomes free variable after unfoldingFootnote
1
. For instance, to compare
![]() ${\mu{\alpha}}.{\alpha \to \textsf{nat}}$
and
${\mu{\alpha}}.{\alpha \to \textsf{nat}}$
and
![]() ${\mu{\alpha}}.{\alpha \to \top}$
, the subtyping statement becomes:
${\mu{\alpha}}.{\alpha \to \top}$
, the subtyping statement becomes:
The one-time unfolding is captured by the labels, since if we ignore the body of the labeled types,
![]() $\alpha \to \textsf{nat}$
and
$\alpha \to \textsf{nat}$
and
![]() $\alpha \to \top$
are compared. On the other hand, when ignoring the labels, the double-unfolding statement is obtained, which exposes the invalid
$\alpha \to \top$
are compared. On the other hand, when ignoring the labels, the double-unfolding statement is obtained, which exposes the invalid
![]() $\top \le \textsf{nat}$
comparison. The key design in the nominal unfolding rules is to use labels as a syntactic device to ensure that recursive types are compared correctly. Without labels providing distinct identities to recursive types, unsound subtyping statements such as
$\top \le \textsf{nat}$
comparison. The key design in the nominal unfolding rules is to use labels as a syntactic device to ensure that recursive types are compared correctly. Without labels providing distinct identities to recursive types, unsound subtyping statements such as
![]() ${\mu{\alpha}}.{\textsf{nat} \to \alpha} \le {\mu{\alpha}}.{\textsf{nat} \to \textsf{nat} \to \top}$
, which unfolds to
${\mu{\alpha}}.{\textsf{nat} \to \alpha} \le {\mu{\alpha}}.{\textsf{nat} \to \textsf{nat} \to \top}$
, which unfolds to
![]() $\textsf{nat} \to \textsf{nat} \to \alpha \le \textsf{nat} \to \textsf{nat} \to \top$
, may be accepted.
$\textsf{nat} \to \textsf{nat} \to \alpha \le \textsf{nat} \to \textsf{nat} \to \top$
, may be accepted.
The nominal unfolding rules are formally proven to be type sound and have the same expressive power as the iso-recursive Amber rules (Zhou et al., Reference Zhou, Oliveira and Fan2022). They are also easier to work with formally, enabling the development of sound and complete algorithmic formulations of subtyping. Additionally, these rules are modular, allowing the extension of existing calculi with iso-recursive types without significant changes to existing definitions and proofs.
2.2 Applications of bounded quantification and recursive types
We now turn to applications of bounded quantification and recursive types. In particular, the classic application for both features is encodings of objects (Bruce et al., Reference Bruce, Cardelli and Pierce1999). In addition, we also show that the two features are useful to model encodings of algebraic datatypes with subtyping.
Object Encodings
A simple and well-known typed encoding of objects is the recursive records encoding (Canning et al., Reference Canning, Cook, Hill and Olthoff1989; Cook et al., Reference Cook, Hill and Canning1989; Bruce et al., Reference Bruce, Cardelli and Pierce1999). In this encoding, the idea is that object types are encoded as recursive record types, and objects are encoded as records.Footnote
2
For example, we can define a type
![]() $\textsf{Point}$
:
$\textsf{Point}$
:
which consists of its coordinates and a
![]() $\textsf{move}$
function. We use a recursive type because move should return an updated point. To implement
$\textsf{move}$
function. We use a recursive type because move should return an updated point. To implement
![]() $\textsf{Point}$
, we define some auxiliary functions:
$\textsf{Point}$
, we define some auxiliary functions:

then a constructor
![]() $\textsf{mkPoint}$
can be defined as:
$\textsf{mkPoint}$
can be defined as:

Note that the auxiliary functions above would not be needed in a source language, since a source language would treat
![]() $\textsf{p.x}$
as syntactic sugar for
$\textsf{p.x}$
as syntactic sugar for
![]() $\textsf{(unfold [Point] p).x}$
. Similarly, the source language would automatically insert a
$\textsf{(unfold [Point] p).x}$
. Similarly, the source language would automatically insert a
![]() $\textsf{fold}$
in the object constructor. In other words, in a source language with iso-recursive subtyping, the
$\textsf{fold}$
in the object constructor. In other words, in a source language with iso-recursive subtyping, the
![]() $\textsf{fold}$
’s and
$\textsf{fold}$
’s and
![]() $\textsf{unfold}$
’s do not need to be explicitly written and are automatically inserted by the compiler. For instance, this is what Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996)’s translation of a language with objects into an iso-recursive extension of
$\textsf{unfold}$
’s do not need to be explicitly written and are automatically inserted by the compiler. For instance, this is what Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996)’s translation of a language with objects into an iso-recursive extension of
![]() $F_{\le}$
does.
$F_{\le}$
does.
With subtyping, we can develop subtypes of
![]() $\textsf{Point}$
, such as:
$\textsf{Point}$
, such as:
 $$\begin{array}{l}\textsf{ColorPoint} {\triangleq} \mu \ \textsf{pnt}. \{ \textsf{x}: \textsf{Int},~ \textsf{y}:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \textsf{pnt},~\textsf{color}: \textsf{String} \}\\\textsf{EqPoint} {\triangleq} \mu \ \textsf{pnt}. \{ \textsf{x}: \textsf{Int},~ \textsf{y}:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \textsf{pnt},~\textsf{eq}: \textsf{pnt} \to \textsf{Bool} \}\end{array}$$
$$\begin{array}{l}\textsf{ColorPoint} {\triangleq} \mu \ \textsf{pnt}. \{ \textsf{x}: \textsf{Int},~ \textsf{y}:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \textsf{pnt},~\textsf{color}: \textsf{String} \}\\\textsf{EqPoint} {\triangleq} \mu \ \textsf{pnt}. \{ \textsf{x}: \textsf{Int},~ \textsf{y}:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \textsf{pnt},~\textsf{eq}: \textsf{pnt} \to \textsf{Bool} \}\end{array}$$
Now, suppose we wish to translate the coordinates by one unit for a point, but we do not want to write such a translation function for each subclass of
![]() $\textsf{Point}$
. As a first attempt, this is achieved with a polymorphic function:
$\textsf{Point}$
. As a first attempt, this is achieved with a polymorphic function:

The type of this
![]() $\textsf{translate}$
function is
$\textsf{translate}$
function is
![]() $\forall({\textsf{P}}\le{\textsf{Point}}).{~ \textsf{P} \to}\textsf{Point}$
, which is obtained from the following typing derivation (some parts omitted):
$\forall({\textsf{P}}\le{\textsf{Point}}).{~ \textsf{P} \to}\textsf{Point}$
, which is obtained from the following typing derivation (some parts omitted):

However, this type is unsatisfying because it loses precision: it returns a
![]() $\textsf{Point}$
instead of a
$\textsf{Point}$
instead of a
![]() $\textsf{P}$
. The type that we want instead is:
$\textsf{P}$
. The type that we want instead is:
Unfortunately, we cannot obtain this more general type with only bounded quantification and the usual unfolding rule typing-unfold. In the rule typing-unfold, the unfold annotation must be a recursive type. However, if we wish to return
![]() $\textsf{P}$
, then we should use
$\textsf{P}$
, then we should use
![]() $\textsf{unfold}$
with the annotation
$\textsf{unfold}$
with the annotation
![]() $\textsf{P}$
, which is not a recursive type, but a type variable.
$\textsf{P}$
, which is not a recursive type, but a type variable.
Some advanced techniques, such as F-bounded quantification (Canning et al., Reference Canning, Cook, Hill and Olthoff1989; Baldan et al., Reference Baldan, Ghelli and Raffaetà1999), address this issue. In F-bounded quantification, the bounded variables are allowed to appear in the bound, and universal types take the form
![]() $\forall({\alpha}\le{F[\alpha]}).{B}$
, where F is a type-level function applied to the bound variable
$\forall({\alpha}\le{F[\alpha]}).{B}$
, where F is a type-level function applied to the bound variable
![]() $\alpha$
. For the example above, the bound in the
$\alpha$
. For the example above, the bound in the
![]() $\textsf{translate}$
function is no longer the closed recursive type
$\textsf{translate}$
function is no longer the closed recursive type
![]() $\textsf{Point}$
but would have the form
$\textsf{Point}$
but would have the form
![]() $F[\alpha] = \{ x: \textsf{Int},~y:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \alpha \}$
. Therefore, with F-bounded quantification, the translate function could have the type:
$F[\alpha] = \{ x: \textsf{Int},~y:\textsf{Int},~ \textsf{move}: \textsf{Int} \to \textsf{Int} \to \alpha \}$
. Therefore, with F-bounded quantification, the translate function could have the type:
Then the
![]() $\alpha$
can be instantiated to
$\alpha$
can be instantiated to
![]() $\textsf{Point}$
or subtypes of
$\textsf{Point}$
or subtypes of
![]() $\textsf{Point}$
, since
$\textsf{Point}$
, since
![]() $\textsf{Point} \le F[\textsf{Point}]$
. Note that to satisfy the F-bounded constraints
$\textsf{Point} \le F[\textsf{Point}]$
. Note that to satisfy the F-bounded constraints
![]() $\alpha \le F[\alpha]$
, the subtyping statements must be interpreted in an equi-recursive setting.
$\alpha \le F[\alpha]$
, the subtyping statements must be interpreted in an equi-recursive setting.
![]() $F_{\le}^{\mu}$
uses a less intrusive approach to achieve the same effect for typing the
$F_{\le}^{\mu}$
uses a less intrusive approach to achieve the same effect for typing the
![]() $\textsf{translate}$
function, without requiring recursive bounds or equi-recursive types. This is achieved by using the structural unfolding rule (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996), which we will discuss in Section 2.3.
$\textsf{translate}$
function, without requiring recursive bounds or equi-recursive types. This is achieved by using the structural unfolding rule (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996), which we will discuss in Section 2.3.
Encoding Positive F-Bounded Quantification
Fortunately, with the structural rules, we can use a type variable as an annotation for
![]() $\textsf{unfold}$
. This enables us to encode forms of F-bounded quantification with positive occurrences of recursive variables, which is the case for
$\textsf{unfold}$
. This enables us to encode forms of F-bounded quantification with positive occurrences of recursive variables, which is the case for
![]() $\textsf{Point}$
. We can change the
$\textsf{Point}$
. We can change the
![]() $\textsf{unfold}$
annotation in
$\textsf{unfold}$
annotation in
![]() $\textsf{translate}$
from the recursive type
$\textsf{translate}$
from the recursive type
![]() $\textsf{Point}$
to its subtype, the type variable
$\textsf{Point}$
to its subtype, the type variable
![]() $\textsf{P}$
:
$\textsf{P}$
:

In Section 2.3, we will discuss the typing of this program via the structural unfolding rule in detail. After this change, the type of
![]() $\textsf{translate}$
is
$\textsf{translate}$
is
![]() $\forall({\textsf{P}}\le{\textsf{Point}}).{\textsf{P} \to \textsf{P}}$
. Then we can apply
$\forall({\textsf{P}}\le{\textsf{Point}}).{\textsf{P} \to \textsf{P}}$
. Then we can apply
![]() $\textsf{translate}$
to
$\textsf{translate}$
to
![]() $\textsf{Point}$
or any of its subtypes, without losing static precision. Thus, if we call
$\textsf{Point}$
or any of its subtypes, without losing static precision. Thus, if we call
![]() $\textsf{translate [EqPoint] (mkEqPoint 0 0)}$
, then we obtain an
$\textsf{translate [EqPoint] (mkEqPoint 0 0)}$
, then we obtain an
![]() $\textsf{EqPoint}$
object at (1,1). Here,
$\textsf{EqPoint}$
object at (1,1). Here,
![]() $\textsf{mkEqPoint}$
is a constructor for objects with type
$\textsf{mkEqPoint}$
is a constructor for objects with type
![]() $\textsf{EqPoint}$
, which contain a binary method (Bruce et al., Reference Bruce, Cardelli, Castagna, Group, Leavens and Pierce1995)
$\textsf{EqPoint}$
, which contain a binary method (Bruce et al., Reference Bruce, Cardelli, Castagna, Group, Leavens and Pierce1995)
![]() $\textsf{eq}$
:
$\textsf{eq}$
:

Encoding Objects with Bounded Existentials
Recursive types are not the only way to encode objects. Another common encoding is to use bounded existentials (Cardelli & Wegner, Reference Cardelli and Wegner1985). Existential types can be used to encode objects (Pierce & Turner, Reference Pierce and Turner1994), or they can be employed together with recursive types (Bruce, Reference Bruce1994). Since the intentional behavior of existential types can be encoded by universal types, we can obtain a form of bounded existentials for free in
![]() $F_\le$
(Cardelli & Wegner, Reference Cardelli and Wegner1985):
$F_\le$
(Cardelli & Wegner, Reference Cardelli and Wegner1985):
 \begin{equation}\begin{array}{c}\begin{array}{rcl} \exists (\alpha \le A).B &\triangleq& \forall({\beta}\le{\top}).{(\forall({\alpha}\le{A}).{B \to \beta \to \beta })} \\ \textsf{pack}~[C, e]~\textsf{as}~({\exists (\alpha \le A).B}) &\triangleq& \Lambda (\beta \le\top).~\lambda (f: \forall({\alpha}\le{A}).{\alpha \to \beta}). f \ C \ e \\ \textsf{unpack}~e_1~\textsf{as}~[\alpha, x]~\textsf{in}~e_2 &\triangleq& e_1 \ C \ (\Lambda (\alpha \le A).~\lambda (x: B). e_2) \\ & & \text{where } e_1 : \exists (\alpha \le A).B \text{ and } e_2 : C\end{array}\end{array}\end{equation}
\begin{equation}\begin{array}{c}\begin{array}{rcl} \exists (\alpha \le A).B &\triangleq& \forall({\beta}\le{\top}).{(\forall({\alpha}\le{A}).{B \to \beta \to \beta })} \\ \textsf{pack}~[C, e]~\textsf{as}~({\exists (\alpha \le A).B}) &\triangleq& \Lambda (\beta \le\top).~\lambda (f: \forall({\alpha}\le{A}).{\alpha \to \beta}). f \ C \ e \\ \textsf{unpack}~e_1~\textsf{as}~[\alpha, x]~\textsf{in}~e_2 &\triangleq& e_1 \ C \ (\Lambda (\alpha \le A).~\lambda (x: B). e_2) \\ & & \text{where } e_1 : \exists (\alpha \le A).B \text{ and } e_2 : C\end{array}\end{array}\end{equation}
Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996) presented an encoding of objects using a combination of recursive types and bounded existential quantification, called the ORBE encoding. In their work, an interface
![]() $I(\alpha)$
is defined as a record of type-level functions, each having a self variable
$I(\alpha)$
is defined as a record of type-level functions, each having a self variable
![]() $\alpha$
argument (
$\alpha$
argument (
![]() $\{l_i : I_i(\alpha)^{i\in 1\ldots n}\}$
). For example, the interface for the
$\{l_i : I_i(\alpha)^{i\in 1\ldots n}\}$
). For example, the interface for the
![]() $\textsf{Point}$
object is:
$\textsf{Point}$
object is:
The general ORBE encoding for an interface
![]() $I(\alpha)$
is:
$I(\alpha)$
is:
 $$\textit{ORBE}(I) \triangleq \mu \alpha. ~ \exists (\beta \le \alpha). ~ \left\{ \begin{array}{l}\textsf{self}: \beta, \\{\textsf{l}_i^{\textsf{sel}}: \beta \to I_i(\beta)}^{\, i \in 1,\ldots, n }, \\{\textsf{l}_i^{\textsf{upd}}: (\beta \to I_i(\beta)) \to \beta}^{\, i \in 1,\ldots, n }\end{array}\right\}$$
$$\textit{ORBE}(I) \triangleq \mu \alpha. ~ \exists (\beta \le \alpha). ~ \left\{ \begin{array}{l}\textsf{self}: \beta, \\{\textsf{l}_i^{\textsf{sel}}: \beta \to I_i(\beta)}^{\, i \in 1,\ldots, n }, \\{\textsf{l}_i^{\textsf{upd}}: (\beta \to I_i(\beta)) \to \beta}^{\, i \in 1,\ldots, n }\end{array}\right\}$$
The bounded existential quantification (
![]() $\exists (\beta \le \alpha)$
) is used to indicate that the true type of an object can be a subtype of the object type
$\exists (\beta \le \alpha)$
) is used to indicate that the true type of an object can be a subtype of the object type
![]() $\alpha$
. Intuitively, it allows the object implementation to contain more fields, such as private variables, than the interface specifies. The field
$\alpha$
. Intuitively, it allows the object implementation to contain more fields, such as private variables, than the interface specifies. The field
![]() $\textsf{self}$
is the object itself with all its methods including private ones so that the listed methods can access the object’s private fields. Through fields
$\textsf{self}$
is the object itself with all its methods including private ones so that the listed methods can access the object’s private fields. Through fields
![]() $\textsf{l_i}^{\textsf{sel}}$
, users of the object can access the object’s public methods. The fields
$\textsf{l_i}^{\textsf{sel}}$
, users of the object can access the object’s public methods. The fields
![]() $\textsf{l_i}^{\textsf{upd}}$
are optional in the encoding. They allow users to update method
$\textsf{l_i}^{\textsf{upd}}$
are optional in the encoding. They allow users to update method
![]() $l_i$
by taking a new function of
$l_i$
by taking a new function of
![]() $\textsf{self}$
and returning a new object with the updated method, which is a feature not supported in many other object encodings. For example, the
$\textsf{self}$
and returning a new object with the updated method, which is a feature not supported in many other object encodings. For example, the
![]() $\textsf{Point}$
object from above can be encoded with the ORBE encoding as follows:
$\textsf{Point}$
object from above can be encoded with the ORBE encoding as follows:
 $$\begin{array}{l}\textsf{Point}_{\textit{ORBE}} {\triangleq} \mu \ \textsf{pnt}.~ \exists (\beta \le \textsf{pnt}).~\left\{\begin{array}{l}\textsf{self}: \beta, \\\textsf{x}^\textsf{sel} : \beta \to \textsf{Int}, \quad \textsf{x}^\textsf{upd}: (\beta \to \textsf{Int}) \to \beta, \\\textsf{y}^\textsf{sel}: \beta \to \textsf{Int}, \quad\textsf{y}^\textsf{upd}: (\beta \to \textsf{Int}) \to \beta, \\\textsf{move}^\textsf{sel}: \beta \to \textsf{Int} \to \textsf{Int} \to \beta, \\\textsf{move}^\textsf{upd}: (\beta \to \textsf{Int} \to \textsf{Int} \to \beta) \to \beta\end{array}\right\}\end{array}$$
$$\begin{array}{l}\textsf{Point}_{\textit{ORBE}} {\triangleq} \mu \ \textsf{pnt}.~ \exists (\beta \le \textsf{pnt}).~\left\{\begin{array}{l}\textsf{self}: \beta, \\\textsf{x}^\textsf{sel} : \beta \to \textsf{Int}, \quad \textsf{x}^\textsf{upd}: (\beta \to \textsf{Int}) \to \beta, \\\textsf{y}^\textsf{sel}: \beta \to \textsf{Int}, \quad\textsf{y}^\textsf{upd}: (\beta \to \textsf{Int}) \to \beta, \\\textsf{move}^\textsf{sel}: \beta \to \textsf{Int} \to \textsf{Int} \to \beta, \\\textsf{move}^\textsf{upd}: (\beta \to \textsf{Int} \to \textsf{Int} \to \beta) \to \beta\end{array}\right\}\end{array}$$
We can implement the
![]() $\textsf{Point}$
object with the ORBE encoding as follows:
$\textsf{Point}$
object with the ORBE encoding as follows:

Method calls are encoded by unfoldings of iso-recursive types and unpacking of bounded existentials. For example, accessing the
![]() $\textsf{x}$
field of a
$\textsf{x}$
field of a
![]() $\textsf{Point}$
object can be implemented as:
$\textsf{Point}$
object can be implemented as:

We omit the encodings for the method update fields in the
![]() $\textsf{mkPointORBE}$
function for brevity, but they can also be written using
$\textsf{mkPointORBE}$
function for brevity, but they can also be written using
![]() $F_{\le}^{\mu}$
. More details about the encoding can be found in the original work (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996). As we can see, the ORBE encoding requires both recursive types and bounded existentials. By rewriting all bounded existentials into universal quantification using (2.1), we are able to write all the programs and types in the ORBE encoding presented above in our
$F_{\le}^{\mu}$
. More details about the encoding can be found in the original work (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996). As we can see, the ORBE encoding requires both recursive types and bounded existentials. By rewriting all bounded existentials into universal quantification using (2.1), we are able to write all the programs and types in the ORBE encoding presented above in our
![]() $F_{\le}^{\mu}$
calculus. Therefore,
$F_{\le}^{\mu}$
calculus. Therefore,
![]() $F_{\le}^{\mu}$
can serve as a target language for the ORBE encoding.
$F_{\le}^{\mu}$
can serve as a target language for the ORBE encoding.
When it comes to subtyping, as Bruce et al. (Reference Bruce, Cardelli and Pierce1999) observe, the ORBE encoding requires
![]() $\textrm{full}~F_{\le}$
for the bounded quantification subtyping rule. Consider the encoding for the object
$\textrm{full}~F_{\le}$
for the bounded quantification subtyping rule. Consider the encoding for the object
![]() $\textsf{ColorPoint}$
, which has more fields than
$\textsf{ColorPoint}$
, which has more fields than
![]() $\textsf{Point}$
.
$\textsf{Point}$
. ![]() should extend the record in
should extend the record in ![]() with
with
![]() $\textsf{color}^\textsf{sel}$
and
$\textsf{color}^\textsf{sel}$
and
![]() $\textsf{color}^\textsf{upd}$
fields. When we try to compare the two encodings, we see that the bounds in
$\textsf{color}^\textsf{upd}$
fields. When we try to compare the two encodings, we see that the bounds in
![]() $(\beta \le \textsf{pnt})$
for the two types are not the same – the recursive variable
$(\beta \le \textsf{pnt})$
for the two types are not the same – the recursive variable
![]() $\textsf{pnt}$
in
$\textsf{pnt}$
in ![]() stands for more fields than in
stands for more fields than in ![]() . As a result, contravariant subtyping is needed for comparing the bound in the existential type, which in turn requires
. As a result, contravariant subtyping is needed for comparing the bound in the existential type, which in turn requires
![]() $\textrm{full}~F_{\le}$
instead of
$\textrm{full}~F_{\le}$
instead of
![]() $\textrm{kernel}~F_{\le}$
. Therefore, we also study the
$\textrm{kernel}~F_{\le}$
. Therefore, we also study the
![]() $\textrm{full}~F_{\le}^{\mu}$
calculus in this paper in order to support subtyping between objects in the ORBE encoding.
$\textrm{full}~F_{\le}^{\mu}$
calculus in this paper in order to support subtyping between objects in the ORBE encoding.
Encodings of Algebraic Datatypes with Subtyping
It is well known that, in the polymorphic lambda calculus (System F) (Reynolds, Reference Reynolds1974), we can use Church (Reference Church1932) encodings to encode algebraic datatypes (Böhm & Berarducci, Reference Böhm and Berarducci1985). However, Church encodings make it hard to encode some operations, or worse they prevent encoding certain operations with the correct time complexity. A well-known example (Church, Reference Church1932) is the encoding of the predecessor function on natural numbers, which is linear with Church encodings instead of being constant time.
An alternative encoding that captures the intentional behavior of datatypes in the untyped lambda calculus and avoids the issues of Church encodings is due to Scott (Reference Scott1962). Unfortunately, Scott encodings cannot be encoded in plain System F. The addition of recursive types to a polymorphic lambda calculus allows a typed Scott encoding (Parigot, Reference Parigot1992). Moreover, in the presence of subtyping, we can also encode algebraic datatypes with subtyping, enabling certain forms of reuse that are not possible without subtyping. Oliveira (Reference Oliveira2009) has shown this assuming a
![]() $F_{\le}$
-like language with recursive types and records, but he has not formalized such a language. Here, we revisit Oliveira’s example. A similar encoding for datatypes can be achieved in
$F_{\le}$
-like language with recursive types and records, but he has not formalized such a language. Here, we revisit Oliveira’s example. A similar encoding for datatypes can be achieved in
![]() $F_{\le}^{\mu}$
. For example, one may define a datatype
$F_{\le}^{\mu}$
. For example, one may define a datatype
![]() $\textsf{Exp}_1$
for mathematical expressions, with constant, addition, and subtraction constructors:
$\textsf{Exp}_1$
for mathematical expressions, with constant, addition, and subtraction constructors:
The encoding in
![]() $F_{\le}^{\mu}$
of this datatype can be defined as follows:
$F_{\le}^{\mu}$
of this datatype can be defined as follows:
If we unfold the recursive type, this encoding is a polymorphic higher-order function that takes a record with three fields (
![]() $\textsf{num}$
,
$\textsf{num}$
,
![]() $\textsf{add}$
, and
$\textsf{add}$
, and
![]() $\textsf{sub}$
) as input. Each field corresponds to a constructor in the datatype definition. This encoding is particularly useful for case analysis, since the polymorphic function essentially encodes case analysis directly. To write a function that performs case analysis on this datatype, one can unfold the recursive type, instantiate
$\textsf{sub}$
) as input. Each field corresponds to a constructor in the datatype definition. This encoding is particularly useful for case analysis, since the polymorphic function essentially encodes case analysis directly. To write a function that performs case analysis on this datatype, one can unfold the recursive type, instantiate
![]() $\textsf{A}$
with the result type, and then provide a record that maps each case to an implementation function that takes the constructor components as input and returns a result of type
$\textsf{A}$
with the result type, and then provide a record that maps each case to an implementation function that takes the constructor components as input and returns a result of type
![]() $\textsf{A}$
. For example, given an expression
$\textsf{A}$
. For example, given an expression
![]() $\textsf{e}$
with type
$\textsf{e}$
with type
![]() $\textsf{Exp}_1$
, a case analysis-based evaluation function can be written as:
$\textsf{Exp}_1$
, a case analysis-based evaluation function can be written as:

where we use
![]() $[\ldots]$
to represent type instantiation. Here,
$[\ldots]$
to represent type instantiation. Here,
![]() $\textsf{Exp}_1$
is instantiated with the evaluation result type
$\textsf{Exp}_1$
is instantiated with the evaluation result type
![]() $\textsf{Int}$
. A record of three functions is supplied to implement case analysis. The
$\textsf{Int}$
. A record of three functions is supplied to implement case analysis. The
![]() $\textsf{num}$
field implements a function that returns the integer
$\textsf{num}$
field implements a function that returns the integer
![]() $\textsf{n}$
of the
$\textsf{n}$
of the
![]() $\textsf{Num}$
constructor directly, while the functions in
$\textsf{Num}$
constructor directly, while the functions in
![]() $\textsf{add}$
and
$\textsf{add}$
and
![]() $\textsf{sub}$
fields perform the evaluation process recursively. To construct concrete instances of the datatype, each constructor also comes with a corresponding encoding in the calculus:
$\textsf{sub}$
fields perform the evaluation process recursively. To construct concrete instances of the datatype, each constructor also comes with a corresponding encoding in the calculus:

One can easily check, using typing-fold, that the result type of each constructor encoding becomes
![]() $\textsf{Exp}_1$
after a recursive type folding. Therefore, in this encoding, the use of constructors and case analysis functions is natural: one can construct the expression
$\textsf{Exp}_1$
after a recursive type folding. Therefore, in this encoding, the use of constructors and case analysis functions is natural: one can construct the expression
![]() $1 + 2$
directly with the encoded constructors as
$1 + 2$
directly with the encoded constructors as
![]() $\textsf{Add}_1~(\textsf{Num}_1 \ 1) \ (\textsf{Num}_1 \ 2)$
and get its evaluation result by calling
$\textsf{Add}_1~(\textsf{Num}_1 \ 1) \ (\textsf{Num}_1 \ 2)$
and get its evaluation result by calling
![]() $\textsf{eval} \ (\textsf{Add}_1~(\textsf{Num}_1 \ 1) \ (\textsf{Num}_1 \ 2))$
.
$\textsf{eval} \ (\textsf{Add}_1~(\textsf{Num}_1 \ 1) \ (\textsf{Num}_1 \ 2))$
.
Subtyping Between Datatypes
Now consider a larger datatype
![]() $\textsf{Exp}$
$\textsf{Exp}$
![]() $_2$
, which extends the
$_2$
, which extends the
![]() $\textsf{Exp}$
$\textsf{Exp}$
![]() $_1$
datatype with a new constructor
$_1$
datatype with a new constructor
![]() $\textsf{Neg}$
, for denoting negative numbers.
$\textsf{Neg}$
, for denoting negative numbers.
This datatype is encoded in
![]() $F_{\le}^{\mu}$
as:
$F_{\le}^{\mu}$
as:
The datatype
![]() $\textsf{Exp}_2$
differs from
$\textsf{Exp}_2$
differs from
![]() $\textsf{Exp}_1$
only in the new constructor: the other constructors are just the same. To reduce code duplication, it is desired that the constructor functions such as
$\textsf{Exp}_1$
only in the new constructor: the other constructors are just the same. To reduce code duplication, it is desired that the constructor functions such as
![]() $\textsf{Add}_1$
can be polymorphic and used for both datatypes. Note that
$\textsf{Add}_1$
can be polymorphic and used for both datatypes. Note that
![]() $\textsf{Exp}_2$
has more constructors than
$\textsf{Exp}_2$
has more constructors than
![]() $\textsf{Exp}_1$
, so it should be safe to coerce
$\textsf{Exp}_1$
, so it should be safe to coerce
![]() $\textsf{Exp}_1$
expressions into
$\textsf{Exp}_1$
expressions into
![]() $\textsf{Exp}_2$
expressions, that is,
$\textsf{Exp}_2$
expressions, that is,
![]() $\textsf{Exp}_1 \le \textsf{Exp}_2$
. Therefore, we would like the
$\textsf{Exp}_1 \le \textsf{Exp}_2$
. Therefore, we would like the
![]() $F_{\le}^{\mu}$
encoding for the
$F_{\le}^{\mu}$
encoding for the
![]() $\textsf{Add}$
constructor to have the following type so that both encodings of
$\textsf{Add}$
constructor to have the following type so that both encodings of
![]() $\textsf{Exp}_1$
and
$\textsf{Exp}_1$
and
![]() $\textsf{Exp}_2$
can use this constructor function:
$\textsf{Exp}_2$
can use this constructor function:
There are two problems here. First, similarly to the issue that we have faced in the translate function, we would like to use a type variable in the fold’s of the constructors. This way we can make the constructors polymorphic. Second, as evidenced by the desired type for Add, we need lower bounded quantification, but in
![]() $F_{\le}^{\mu}$
(and
$F_{\le}^{\mu}$
(and
![]() $F_{\le}$
) we only have upper bounded quantification.
$F_{\le}$
) we only have upper bounded quantification.
Polymorphic Constructors with Lower Bounded Quantification
For applications such as encodings of algebraic datatypes, the dual form of bounded quantification (lower bounded quantification) seems to be more useful. Thus, we have an extended system, called
![]() $F_{\le\ge}^{\mu\wedge}$
, that also supports lower bounded quantification. Polymorphic datatype constructors become typeable with the structural folding rule. For example, we can encode the polymorphic Add constructor as:
$F_{\le\ge}^{\mu\wedge}$
, that also supports lower bounded quantification. Polymorphic datatype constructors become typeable with the structural folding rule. For example, we can encode the polymorphic Add constructor as:
Other polymorphic constructors such as
![]() $\textsf{Num}_\forall$
and
$\textsf{Num}_\forall$
and
![]() $\textsf{Sub}_\forall$
can be encoded similarly, enabling more useful programming patterns. For example, if we want to implement a compiler that uses
$\textsf{Sub}_\forall$
can be encoded similarly, enabling more useful programming patterns. For example, if we want to implement a compiler that uses
![]() $\textsf{Exp}_1$
as its core language, but also want to support richer datatype constructors in a source language like
$\textsf{Exp}_1$
as its core language, but also want to support richer datatype constructors in a source language like
![]() $\textsf{Exp}_2$
does, we would like to be able to reduce code duplication across the two similar languages. For instance, if we define a pretty printer function for
$\textsf{Exp}_2$
does, we would like to be able to reduce code duplication across the two similar languages. For instance, if we define a pretty printer function for
![]() $\textsf{Exp}_2$
$\textsf{Exp}_2$

we can use this function to print
![]() $\textsf{Exp}_1$
expressions as well: all the constructors in
$\textsf{Exp}_1$
expressions as well: all the constructors in
![]() $\textsf{Exp}_1$
are also in
$\textsf{Exp}_1$
are also in
![]() $\textsf{Exp}_2$
and have their pretty printing methods defined in the above function.
$\textsf{Exp}_2$
and have their pretty printing methods defined in the above function.
Suppose also that we wish to implement a simple desugaring function that transforms
![]() $\textsf{Exp}_2$
into
$\textsf{Exp}_2$
into
![]() $\textsf{Exp}_1$
, by transforming negative numbers
$\textsf{Exp}_1$
, by transforming negative numbers
![]() $-n$
into subtractions
$-n$
into subtractions
![]() $0-n$
. This function should do case analysis on
$0-n$
. This function should do case analysis on
![]() $\textsf{Exp}_2$
and use only the constructors in
$\textsf{Exp}_2$
and use only the constructors in
![]() $\textsf{Exp}_1$
to produce the result, that is, it should have a type
$\textsf{Exp}_1$
to produce the result, that is, it should have a type
![]() $\textsf{Exp}_2 \to \textsf{Exp}_1$
. The following code, with polymorphic constructors, has the desired typing:
$\textsf{Exp}_2 \to \textsf{Exp}_1$
. The following code, with polymorphic constructors, has the desired typing:

In contrast, in many practical programming languages, this task involves either code duplication or loss of type precision. In a typical functional language, we can define both
![]() $\textsf{Exp}_1$
and
$\textsf{Exp}_1$
and
![]() $\textsf{Exp}_2$
and also obtain precise static typing guarantees for the desugar function. But this comes at the cost of duplication, since the constructors for the two datatypes are different, and many operations, such as pretty printing, need to be essentially duplicated. In
$\textsf{Exp}_2$
and also obtain precise static typing guarantees for the desugar function. But this comes at the cost of duplication, since the constructors for the two datatypes are different, and many operations, such as pretty printing, need to be essentially duplicated. In
![]() $F_{\le\ge}^{\mu\wedge}$
, in addition to polymorphic constructors, we would just need to define the pretty printer for
$F_{\le\ge}^{\mu\wedge}$
, in addition to polymorphic constructors, we would just need to define the pretty printer for
![]() $\textsf{Exp}_2$
, and that function would also work for
$\textsf{Exp}_2$
, and that function would also work for
![]() $\textsf{Exp}_1$
. Alternatively, in a typical functional language, one could define only
$\textsf{Exp}_1$
. Alternatively, in a typical functional language, one could define only
![]() $\textsf{Exp}_2$
and type desugar with the imprecise type
$\textsf{Exp}_2$
and type desugar with the imprecise type
![]() $\textsf{Exp}_2 \to \textsf{Exp}_2$
, which does not statically guarantee that the Neg constructor has been removed. This solution avoids the duplication at the cost of static typing guarantees. In
$\textsf{Exp}_2 \to \textsf{Exp}_2$
, which does not statically guarantee that the Neg constructor has been removed. This solution avoids the duplication at the cost of static typing guarantees. In
![]() $F_{\le\ge}^{\mu\wedge}$
, we do not need such compromises: we can avoid code duplication and preserve the static typing guarantees.
$F_{\le\ge}^{\mu\wedge}$
, we do not need such compromises: we can avoid code duplication and preserve the static typing guarantees.
2.3 Key ideas and results
As Table 1 shows, no previous calculi with bounded quantification and recursive types are fully satisfactory in all dimensions. In particular, equi-recursive types are problematic, since they can change the expressive power of the subtyping relation in unexpected ways. More importantly, adding equi-recursive subtyping to
![]() $F_{\le}$
requires novel algorithms, and the extension is non-modular, requiring several changes to existing definitions and proofs.
$F_{\le}$
requires novel algorithms, and the extension is non-modular, requiring several changes to existing definitions and proofs.
Kernel
 $F_{\le}$
with Iso-Recursive Types
$F_{\le}$
with Iso-Recursive Types
Our type system directly combines
![]() $\textrm{kernel}~F_{\le}$
and the nominal unfolding rules together. The addition of the nominal unfolding rules has almost no effect on the original proofs in
$\textrm{kernel}~F_{\le}$
and the nominal unfolding rules together. The addition of the nominal unfolding rules has almost no effect on the original proofs in
![]() $\textrm{kernel}~F_{\le}$
. That is, the proofs for important lemmas, such as transitivity, are nearly the same as those in
$\textrm{kernel}~F_{\le}$
. That is, the proofs for important lemmas, such as transitivity, are nearly the same as those in
![]() $\textrm{kernel}~F_{\le}$
, except that we need a new case to deal with recursive types. Thus, proofs that have been very hard in the past, such as transitivity, are very simple in
$\textrm{kernel}~F_{\le}$
, except that we need a new case to deal with recursive types. Thus, proofs that have been very hard in the past, such as transitivity, are very simple in
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
The more challenging aspect in the metatheory of
![]() $F_{\le}^{\mu}$
lies in the unfolding lemma:
$F_{\le}^{\mu}$
lies in the unfolding lemma:
which reveals an important property for iso-recursive types: if two iso-recursive types are subtypes, then their one-step unfoldings are also subtypes. To prove the unfolding lemma, a generalized lemma is needed (Zhou et al., Reference Zhou, Oliveira and Fan2022). In
![]() $F_{\le}^{\mu}$
, we show that the previous generalized approach is insufficient due to bounded quantification. Therefore, an even more general lemma is proposed.
$F_{\le}^{\mu}$
, we show that the previous generalized approach is insufficient due to bounded quantification. Therefore, an even more general lemma is proposed.
Another challenge is decidability. Although both
![]() $\textrm{kernel}~F_{\le}$
and the nominal unfolding rules (for simple calculi) have been independently proved decidable, their decidability proofs use very different measures. A natural combination is problematic; thus, we need a new approach.
$\textrm{kernel}~F_{\le}$
and the nominal unfolding rules (for simple calculi) have been independently proved decidable, their decidability proofs use very different measures. A natural combination is problematic; thus, we need a new approach.
After overcoming those challenges, we show that kernel
![]() $F_{\le}^{\mu}$
is transitive, decidable, conservative, and modular. Furthermore, there is a simple, sound, and complete algorithmic type system to enable implementations and to provide important help in the proofs of results such as conservativity of typing.
$F_{\le}^{\mu}$
is transitive, decidable, conservative, and modular. Furthermore, there is a simple, sound, and complete algorithmic type system to enable implementations and to provide important help in the proofs of results such as conservativity of typing.
Full
 $F_{\le}$
with Iso-Recursive Types
$F_{\le}$
with Iso-Recursive Types
We have also integrated
![]() $\textrm{full}~F_{\le}$
with iso-recursive subtyping. The most significant challenge compared to the kernel variant is proving the unfolding lemma. As we will discuss in Section 4.3, the method used to prove the generalized unfolding lemma for the kernel variant does not apply to the full variant due to the contravariance of the bounds. Therefore, a yet more sophisticated adaptation of the generalized unfolding lemma is required. Additionally, we establish several other properties for full
$\textrm{full}~F_{\le}$
with iso-recursive subtyping. The most significant challenge compared to the kernel variant is proving the unfolding lemma. As we will discuss in Section 4.3, the method used to prove the generalized unfolding lemma for the kernel variant does not apply to the full variant due to the contravariance of the bounds. Therefore, a yet more sophisticated adaptation of the generalized unfolding lemma is required. Additionally, we establish several other properties for full
![]() $F_{\le}^{\mu}$
, such as type soundness, conservativity, and undecidability.
$F_{\le}^{\mu}$
, such as type soundness, conservativity, and undecidability.
Structural Folding and Unfolding Rules
In our work, instead of standard rules for fold/unfold expressions, we use structural rules:

The key point about the structural rules is that the annotations are generalized to be a subtype/supertype of a recursive type, instead of exactly a recursive type. In particular, this generalization enables annotating fold/unfold with a bounded type variable. This is forbidden in the traditional rules. In the typing-sunfold, it is worthwhile to mention that when we have
![]() $A \le {\mu{\alpha}}.{B}$
where
$A \le {\mu{\alpha}}.{B}$
where
![]() $\alpha$
appears negatively in B, then there are very limited choices to what A can be. Essentially, it can be
$\alpha$
appears negatively in B, then there are very limited choices to what A can be. Essentially, it can be
![]() ${\mu{\alpha}}.{B}$
itself and little else. In other words, negative recursive types have very restricted subtyping, which is why the structural unfolding rule can be type safe. Note also that, since the structural unfolding rules provide almost no flexibility for negative recursive subtyping, they are insufficient to fully express F-bounded quantification for negative recursive types.
${\mu{\alpha}}.{B}$
itself and little else. In other words, negative recursive types have very restricted subtyping, which is why the structural unfolding rule can be type safe. Note also that, since the structural unfolding rules provide almost no flexibility for negative recursive subtyping, they are insufficient to fully express F-bounded quantification for negative recursive types.
The structural unfolding rule was presented by Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996) for supporting structural updates in the object calculus that was being encoded into
![]() $F_{\le}$
with iso-recursive types. In their work, the structural unfolding rule is presented with an informal explanation. We provide structural rules for both unfold and fold expressions, together with the formalization of the type soundness for both rules. With the structural unfolding rule we can, for instance, obtain the desired typing for the translate function.
$F_{\le}$
with iso-recursive types. In their work, the structural unfolding rule is presented with an informal explanation. We provide structural rules for both unfold and fold expressions, together with the formalization of the type soundness for both rules. With the structural unfolding rule we can, for instance, obtain the desired typing for the translate function.

Readers can compare this derivation to the one in Section 2.2, where the conventional unfolding rule and the subsumption rule are used instead. The use of typing-sunfold enables us to give a more precise type for the translate function.
Lower Bounded Quantification and
 $F_{\le\ge}^{\mu\wedge}$
$F_{\le\ge}^{\mu\wedge}$
We have also formalized an extension of
![]() $F_{\le}^{\mu}$
with both upper and lower bounded quantification, called
$F_{\le}^{\mu}$
with both upper and lower bounded quantification, called
![]() $F_{\le\ge}^{\mu\wedge}$
. All the same results that are proved for
$F_{\le\ge}^{\mu\wedge}$
. All the same results that are proved for
![]() $F_{\le}^{\mu}$
are also proved for
$F_{\le}^{\mu}$
are also proved for
![]() $F_{\le\ge}^{\mu\wedge}$
, including transitivity, decidability, and type soundness. The structural folding rules become more useful in
$F_{\le\ge}^{\mu\wedge}$
, including transitivity, decidability, and type soundness. The structural folding rules become more useful in
![]() $F_{\le\ge}^{\mu\wedge}$
. With lower bounded quantification and the structural folding rules, we can get the correct typing for the polymorphic Add constructor:
$F_{\le\ge}^{\mu\wedge}$
. With lower bounded quantification and the structural folding rules, we can get the correct typing for the polymorphic Add constructor:

Records as Intersection Types
It is well known that multi-field records can be encoded using intersection types and single-field records (Reynolds, Reference Reynolds1988; Dunfield, Reference Dunfield2012). In
![]() $F_{\le\ge}^{\mu\wedge}$
, we follow this alternative approach to type record expressions. The record type
$F_{\le\ge}^{\mu\wedge}$
, we follow this alternative approach to type record expressions. The record type
![]() $\{\textsf{x} : \textsf{nat}, \textsf{y} : \textsf{nat}\}$
in
$\{\textsf{x} : \textsf{nat}, \textsf{y} : \textsf{nat}\}$
in
![]() $F_{\le}^{\mu}$
is now simply syntactic sugar in
$F_{\le}^{\mu}$
is now simply syntactic sugar in
![]() $F_{\le\ge}^{\mu\wedge}$
for the intersection type
$F_{\le\ge}^{\mu\wedge}$
for the intersection type
![]() $\{\textsf{x} : \textsf{nat}\} \& \{\textsf{y} : \textsf{nat}\}$
. To avoid records with duplicate labels being intersected, we restrict the labels in the intersection types to be disjoint. For instance,
$\{\textsf{x} : \textsf{nat}\} \& \{\textsf{y} : \textsf{nat}\}$
. To avoid records with duplicate labels being intersected, we restrict the labels in the intersection types to be disjoint. For instance,
![]() $\{x : \textsf{nat}\} \,\&\, \{x : \textsf{nat} \to \textsf{nat}\}$
is not a valid type in
$\{x : \textsf{nat}\} \,\&\, \{x : \textsf{nat} \to \textsf{nat}\}$
is not a valid type in
![]() $F_{\le\ge}^{\mu\wedge}$
. We will further discuss such design choice in Section 5. The combination of unrestricted intersection types and iso-recursive subtyping was studied by Zhou et al. (Reference Zhou, Oliveira and Fan2022). Our work models a restricted form of intersection types. In
$F_{\le\ge}^{\mu\wedge}$
. We will further discuss such design choice in Section 5. The combination of unrestricted intersection types and iso-recursive subtyping was studied by Zhou et al. (Reference Zhou, Oliveira and Fan2022). Our work models a restricted form of intersection types. In
![]() $F_{\le\ge}^{\mu\wedge}$
, only types that are formed by intersecting single-field record types are considered, and the disjointness relation discussed in Zhou et al. (Reference Zhou, Oliveira and Fan2022) is in turn simplified to a compatibility relation for checking well-formedness of intersection types. The intersection type operator
$F_{\le\ge}^{\mu\wedge}$
, only types that are formed by intersecting single-field record types are considered, and the disjointness relation discussed in Zhou et al. (Reference Zhou, Oliveira and Fan2022) is in turn simplified to a compatibility relation for checking well-formedness of intersection types. The intersection type operator
![]() $\&$
is commutative and associative in terms of type equivalence so that record permutations are obtained for free.
$\&$
is commutative and associative in terms of type equivalence so that record permutations are obtained for free.
The typing rules for record expressions and projections in
![]() $F_{\le\ge}^{\mu\wedge}$
are shown below:
$F_{\le\ge}^{\mu\wedge}$
are shown below:

With intersection types, record expressions are now typed using rule typing-srcd. As a result, we no longer need a dedicated rule for subtyping multi-field record types, which has a complicated definition since it needs to decide the subset inclusion of record fields and check the subtyping relation for common fields. Instead, we can now rely on the subtyping relation for intersection types and a direct subtyping rule for subtyping types in single-field records. Moreover, record projections can be defined in terms of subtyping now, as rule typing-sproj shows. When projecting a field from a record expression e, we can simply check if the record type of e is a subtype of the expected record type.
The treatment of records in
![]() $F_{\le\ge}^{\mu\wedge}$
aligns closely with the way DOT (Rompf & Amin, Reference Rompf and Amin2016) deals with object types. Rule typing-dot-object shows the typing rule for object expressions in DOT. In DOT, object expressions are a record with a self reference variable x bounded to the object itself, containing a list of labeled declarations
$F_{\le\ge}^{\mu\wedge}$
aligns closely with the way DOT (Rompf & Amin, Reference Rompf and Amin2016) deals with object types. Rule typing-dot-object shows the typing rule for object expressions in DOT. In DOT, object expressions are a record with a self reference variable x bounded to the object itself, containing a list of labeled declarations
![]() $d_1 \ldots d_n$
. When type checking objects, each declaration is checked on its own, and the intersection of all the declaration types forms the type of the object.
$d_1 \ldots d_n$
. When type checking objects, each declaration is checked on its own, and the intersection of all the declaration types forms the type of the object.

![]() $F_{\le\ge}^{\mu\wedge}$
and DOT share the same idea of using intersection types to type record expressions or objects and both require the labels to be disjoint. Due to the use of path-dependent types (Amin et al., Reference Amin, Rompf and Odersky2014) in DOT, the treatment of recursive types is different. In
$F_{\le\ge}^{\mu\wedge}$
and DOT share the same idea of using intersection types to type record expressions or objects and both require the labels to be disjoint. Due to the use of path-dependent types (Amin et al., Reference Amin, Rompf and Odersky2014) in DOT, the treatment of recursive types is different. In
![]() $F_{\le\ge}^{\mu\wedge}$
, we do not have a self reference variable in record expressions or types, and
$F_{\le\ge}^{\mu\wedge}$
, we do not have a self reference variable in record expressions or types, and
![]() $F_{\le\ge}^{\mu\wedge}$
lacks some DOT features. On the other hand,
$F_{\le\ge}^{\mu\wedge}$
lacks some DOT features. On the other hand,
![]() $F_{\le\ge}^{\mu\wedge}$
has key properties, such as decidability, transitivity of subtyping, and being a conservative extension of
$F_{\le\ge}^{\mu\wedge}$
has key properties, such as decidability, transitivity of subtyping, and being a conservative extension of
![]() $F_{\le}$
, which are partly missing in DOT. Despite these differences, we hope that
$F_{\le}$
, which are partly missing in DOT. Despite these differences, we hope that
![]() $F_{\le\ge}^{\mu\wedge}$
can provide insights into the design of DOT-like calculi with bounded quantification and recursive types and complement the existing work in terms of the design space.
$F_{\le\ge}^{\mu\wedge}$
can provide insights into the design of DOT-like calculi with bounded quantification and recursive types and complement the existing work in terms of the design space.
3 Bounded quantification with iso-recursive types
This section introduces a new calculus, called
![]() $F_{\le}^{\mu}$
, integrating bounded quantification, record types, and recursive types. We show two variants of
$F_{\le}^{\mu}$
, integrating bounded quantification, record types, and recursive types. We show two variants of
![]() $F_{\le}^{\mu}$
. One is kernel
$F_{\le}^{\mu}$
. One is kernel
![]() $F_{\le}^{\mu}$
, by adopting the kernel rule for subtyping bounded quantification from
$F_{\le}^{\mu}$
, by adopting the kernel rule for subtyping bounded quantification from
![]() $\textrm{kernel}~F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985). The other one is full
$\textrm{kernel}~F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985). The other one is full
![]() $F_{\le}^{\mu}$
, which instead adopts the full rule for subtyping bounded quantification from
$F_{\le}^{\mu}$
, which instead adopts the full rule for subtyping bounded quantification from
![]() $\textrm{full}~F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994).
$\textrm{full}~F_{\le}$
(Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994).
3.1 Kernel
 $F_{\le}$
with iso-recursive subtyping
$F_{\le}$
with iso-recursive subtyping
First, we introduce how to combine kernel bounded quantification, multi-field records, and iso-recursive subtyping in
![]() $\textrm{kernel}~F_{\le}^{\mu}$
.
$\textrm{kernel}~F_{\le}^{\mu}$
.
Syntax and Well-Formedness
The syntax of types and contexts for
![]() $F_{\le}^{\mu}$
is shown in Figure 1. Meta-variables A, B, C, D range over types. Types consist of natural numbers (
$F_{\le}^{\mu}$
is shown in Figure 1. Meta-variables A, B, C, D range over types. Types consist of natural numbers (
![]() $\textsf{nat}$
), the top type (
$\textsf{nat}$
), the top type (
![]() $\top$
), function types (
$\top$
), function types (
![]() $A \to B$
), type variables (
$A \to B$
), type variables (
![]() $\alpha$
), recursive types (
$\alpha$
), recursive types (
![]() ${\mu{\alpha}}.{A}$
), labeled types (
${\mu{\alpha}}.{A}$
), labeled types (![]() ), universal types (
), universal types (
![]() $\forall({\alpha}\le{A}).{B}$
), and record types (
$\forall({\alpha}\le{A}).{B}$
), and record types (
![]() $\{ l_i : A_i ~ ^{i \in 1\cdots n} \}$
). Labeled types are types that are annotated with a label. They enable distinguishing between otherwise structurally compatible types (equal types or subtypes). That is if the two types being compared have different labels or one of the types is unlabeled, then the two types will not be related, even when, ignoring the labels, they would be structurally compatible. Expressions, denoted by the meta-variable e, include term variables (x), natural numbers (
$\{ l_i : A_i ~ ^{i \in 1\cdots n} \}$
). Labeled types are types that are annotated with a label. They enable distinguishing between otherwise structurally compatible types (equal types or subtypes). That is if the two types being compared have different labels or one of the types is unlabeled, then the two types will not be related, even when, ignoring the labels, they would be structurally compatible. Expressions, denoted by the meta-variable e, include term variables (x), natural numbers (
![]() $\textsf{i}$
), applications (
$\textsf{i}$
), applications (
![]() $e_1~e_2$
), abstractions (
$e_1~e_2$
), abstractions (
![]() $\lambda x:A .~ e$
), type applications (
$\lambda x:A .~ e$
), type applications (
![]() $e~A$
), type abstractions (
$e~A$
), type abstractions (
![]() $\Lambda (\alpha \le A) .~ e$
), fold expressions (
$\Lambda (\alpha \le A) .~ e$
), fold expressions (
![]() $\textsf{fold}~[A]~e$
), unfold expressions (
$\textsf{fold}~[A]~e$
), unfold expressions (
![]() $\textsf{unfold}~[A]~e$
), records (
$\textsf{unfold}~[A]~e$
), records (
![]() $\{ l_i = e_i ~ ^{i \in 1\cdots n} \}$
), and record selection (
$\{ l_i = e_i ~ ^{i \in 1\cdots n} \}$
), and record selection (
![]() $e.l$
). Among them, natural numbers, abstractions, and type abstractions are values. Fold expressions and records can be values if their inner expressions are also values. The context is used to store type variables with their bounds and term variables with their types. Note that it is not necessary to distinguish recursive variables and universal variables.
$e.l$
). Among them, natural numbers, abstractions, and type abstractions are values. Fold expressions and records can be values if their inner expressions are also values. The context is used to store type variables with their bounds and term variables with their types. Note that it is not necessary to distinguish recursive variables and universal variables.

Fig. 1. Syntax of
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
The definition of a well-formed environment
![]() $\vdash \Gamma$
is standard, ensuring that all variables in the environment are distinct and all types in the environment are well formed. A type is well formed if all of its free variables are in the context. The well-formedness rules for types are shown at the top of Figure 2.
$\vdash \Gamma$
is standard, ensuring that all variables in the environment are distinct and all types in the environment are well formed. A type is well formed if all of its free variables are in the context. The well-formedness rules for types are shown at the top of Figure 2.

Fig. 2. Well-formedness and subtyping rules for kernel
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Subtyping for Kernel
 $F_{\le}^{\mu}$
$F_{\le}^{\mu}$
The bottom of Figure 2 shows the subtyping judgment. Our subtyping rules are mostly standard. The rules essentially include the rules of the algorithmic version of
![]() $\textrm{kernel}~F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994), but the rule for bounded quantification is generalized. The rules S-var,S-vartrans are standard
$\textrm{kernel}~F_{\le}$
(Cardelli & Wegner, Reference Cardelli and Wegner1985; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994), but the rule for bounded quantification is generalized. The rules S-var,S-vartrans are standard
![]() $F_{\le}$
rules. Since we do not distinguish universal and recursive variables, those rules apply also to recursive type variables. The rule for function types (rule S-arrow) is contravariant on the input types and covariant on the output types. We have placed well-formedness checks on all the base cases of the subtyping rules, which ensures that the context and types in a subtyping relation are well formed, as shown in Lemma 3.1. Note that for this regularity property to hold, in rule S-rcd we require the left record type to be well formed but not the right one, since the well-formedness of the right type can be derived from the subtyping relation on record fields, while there might be extra fields in the left record type that are not compared in the subtyping relation.
$F_{\le}$
rules. Since we do not distinguish universal and recursive variables, those rules apply also to recursive type variables. The rule for function types (rule S-arrow) is contravariant on the input types and covariant on the output types. We have placed well-formedness checks on all the base cases of the subtyping rules, which ensures that the context and types in a subtyping relation are well formed, as shown in Lemma 3.1. Note that for this regularity property to hold, in rule S-rcd we require the left record type to be well formed but not the right one, since the well-formedness of the right type can be derived from the subtyping relation on record fields, while there might be extra fields in the left record type that are not compared in the subtyping relation.
Lemma 3.1 (Regularity of subtyping). If
![]() $\Gamma \vdash A \le B$
, then the following well-formedness conditions hold: (1)
$\Gamma \vdash A \le B$
, then the following well-formedness conditions hold: (1)
![]() $\vdash \Gamma$
, (2)
$\vdash \Gamma$
, (2)
![]() $\Gamma \vdash A$
, and (3)
$\Gamma \vdash A$
, and (3)
![]() $\Gamma \vdash B$
.
$\Gamma \vdash B$
.
Subtyping Bounded Quantification
The rule for bounded quantification is interesting, stating that two universal types are subtypes if their bounds are equivalent (i.e. they are subtypes of each other) and the bodies are subtypes. Rule S-equivall is more general than rule S-kernelall since the latter requires the bounds to be equal. The reason to have the more general rule using equivalent bounds is that, for records, we wish to accept subtyping statements such as:
where the bounds can be syntactically different, but equivalent, types. In the presence of records or other features, such as intersection and union types (Pottinger, Reference Pottinger1980; Coppo et al., Reference Coppo, Dezani-Ciancaglini and Venneri1981; Barbanera et al., Reference Barbanera, Dezani-Ciancaglini and de’Liguoro1995), we can have such equivalent but not syntactically equal types. Therefore, we should generalize the rule for bounded quantification to deal with those cases. This generalization to equivalent bounds retains decidable subtyping just as
![]() $\textrm{kernel}~F_{\le}$
as we shall see in Section 4.3.
$\textrm{kernel}~F_{\le}$
as we shall see in Section 4.3.
Subtyping Recursive Types
For dealing with iso-recursive subtyping, we employ the recent nominal unfolding rules (Zhou et al., Reference Zhou, Oliveira and Fan2022), which have equivalent expressive power to the well-known (iso-recursive) Amber rules (Cardelli, Reference Cardelli1985). The nominal unfolding rules have been discussed in Section 2.1. The reason for choosing the nominal unfolding rules is that they enable us to prove important metatheoretical results, such as transitivity, and develop an algorithmic formulation of subtyping.
We extend the rule S-nominal to the rule S-rec in
![]() $F_{\le}^{\mu}$
, by bounding recursive variables with
$F_{\le}^{\mu}$
, by bounding recursive variables with
![]() $\top$
when they are introduced into the context. Therefore, recursive variables are also treated as universal variables, and we do not need to adjust the form of contexts in
$\top$
when they are introduced into the context. Therefore, recursive variables are also treated as universal variables, and we do not need to adjust the form of contexts in
![]() $F_{\le}$
for
$F_{\le}$
for
![]() $F_{\le}^{\mu}$
. Apart from this, no other changes are necessary, making the addition of recursive types mostly noninvasive. Consequently, the proofs of narrowing, reflexivity, and transitivity are the same as the original one for
$F_{\le}^{\mu}$
. Apart from this, no other changes are necessary, making the addition of recursive types mostly noninvasive. Consequently, the proofs of narrowing, reflexivity, and transitivity are the same as the original one for
![]() $F_{\le}$
, except for the new cases dealing with recursive types and minor adjustments to the rule of bounded quantification due to the generalization to equivalent bounds. For those new cases, the proofs are all straightforward from the induction hypothesis.
$F_{\le}$
, except for the new cases dealing with recursive types and minor adjustments to the rule of bounded quantification due to the generalization to equivalent bounds. For those new cases, the proofs are all straightforward from the induction hypothesis.
Lemma 3.2 (Narrowing). If
![]() $\Gamma_1 \vdash C \le C'$
and
$\Gamma_1 \vdash C \le C'$
and
![]() $\Gamma_1, \alpha\le C' ,\Gamma_2 \vdash A \le B$
, then
$\Gamma_1, \alpha\le C' ,\Gamma_2 \vdash A \le B$
, then
![]() $\Gamma_1, \alpha\le C ,\Gamma_2 \vdash A \le B$
.
$\Gamma_1, \alpha\le C ,\Gamma_2 \vdash A \le B$
.
Theorem 3.3 (Reflexivity). If
![]() $\vdash \Gamma$
and
$\vdash \Gamma$
and
![]() $\Gamma \vdash A$
, then
$\Gamma \vdash A$
, then
![]() $\Gamma \vdash A \le A$
.
$\Gamma \vdash A \le A$
.
Theorem 3.4 (Transitivity). If
![]() $\Gamma \vdash A \le B$
and
$\Gamma \vdash A \le B$
and
![]() $\Gamma \vdash B \le C$
, then
$\Gamma \vdash B \le C$
, then
![]() $\Gamma \vdash A \le C$
.
$\Gamma \vdash A \le C$
.
The Unfolding Lemma
Another important lemma is the unfolding lemma, which reveals that, if two recursive types are subtypes, then their unfoldings are also subtypes. The unfolding lemma is important for proving type preservation in a calculus with iso-recursive subtyping. A key difficulty in the formalization of
![]() $F_{\le}^{\mu}$
is proving the unfolding lemma which, due to the presence of bounded quantification, requires a different proof technique compared to the proofs by Zhou et al. (Reference Zhou, Oliveira and Fan2022). We discuss the proof of the unfolding lemma in Section 4.1.
$F_{\le}^{\mu}$
is proving the unfolding lemma which, due to the presence of bounded quantification, requires a different proof technique compared to the proofs by Zhou et al. (Reference Zhou, Oliveira and Fan2022). We discuss the proof of the unfolding lemma in Section 4.1.
Lemma 3.5 (Unfolding Lemma). If
![]() $\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
, then
$\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
, then
![]() $\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{A}]~A \le [\alpha \mapsto {\mu{\alpha}}.{B}]~B$
.
$\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{A}]~A \le [\alpha \mapsto {\mu{\alpha}}.{B}]~B$
.
3.2 Full
 $F_{\le}$
with iso-recursive subtyping
$F_{\le}$
with iso-recursive subtyping
In full
![]() $F_{\le}^{\mu}$
, which incorporates
$F_{\le}^{\mu}$
, which incorporates
![]() $\textrm{full}~F_{\le}$
and iso-recursive types, the sole distinction from the kernel variant of
$\textrm{full}~F_{\le}$
and iso-recursive types, the sole distinction from the kernel variant of
![]() $F_{\le}^{\mu}$
lies in permitting contravariant bounds, so we only present the differences between the two variants.
$F_{\le}^{\mu}$
lies in permitting contravariant bounds, so we only present the differences between the two variants.
Syntax and Subtyping
The syntax of the full
![]() $F_{\le}^{\mu}$
is identical to that of the kernel
$F_{\le}^{\mu}$
is identical to that of the kernel
![]() $F_{\le}^{\mu}$
(Section 3.1). As for the subtyping rules, rule S-equivall is replaced by rule S-fullall in full
$F_{\le}^{\mu}$
(Section 3.1). As for the subtyping rules, rule S-equivall is replaced by rule S-fullall in full
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.

The only distinction between these two rules lies in the variance of the bounds: rule S-fullall permits contravariance, allowing
![]() $A_2$
to be a subtype of
$A_2$
to be a subtype of
![]() $A_1$
, whereas rule S-equivall demands
$A_1$
, whereas rule S-equivall demands
![]() $A_2$
to be equivalent to
$A_2$
to be equivalent to
![]() $A_1$
. The change to the subtyping rules in full
$A_1$
. The change to the subtyping rules in full
![]() $F_{\le}^{\mu}$
does not impact many subtyping lemmas, such as reflexivity (Theorem 3.3) and transitivity (Theorem 3.4), which remain provable by reusing proof techniques from
$F_{\le}^{\mu}$
does not impact many subtyping lemmas, such as reflexivity (Theorem 3.3) and transitivity (Theorem 3.4), which remain provable by reusing proof techniques from
![]() $\textrm{full}~F_{\le}$
. However, as we shall see in Section 4.1, the unfolding lemma (Lemma 3.5) needs a different proof technique due to the presence of contravariant bounds in full
$\textrm{full}~F_{\le}$
. However, as we shall see in Section 4.1, the unfolding lemma (Lemma 3.5) needs a different proof technique due to the presence of contravariant bounds in full
![]() $F_{\le}^{\mu}$
. In Section 4.1, we will present a new generalized unfolding lemma that can be proved in both kernel and full
$F_{\le}^{\mu}$
. In Section 4.1, we will present a new generalized unfolding lemma that can be proved in both kernel and full
![]() $F_{\le}^{\mu}$
. With this new lemma, we can prove the unfolding lemma (Lemma 3.5) for full
$F_{\le}^{\mu}$
. With this new lemma, we can prove the unfolding lemma (Lemma 3.5) for full
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
3.3 Typing, reduction, and type soundness
The two variants of the subtyping rules have no impact on proving type soundness. Therefore, the typing and reduction rules remain consistent across both variants. Figure 3 shows the typing rules and reduction rules. Most rules are standard except for the typing rules for unfold and fold. For these two expressions, we use structural rules instead (rule typing-sunfold and typing-sfold), as explained in Section 2.3.

Fig. 3. Typing and reduction rules.
Structural Unfolding Lemma
Since the typing rules that we adopt for fold/unfold expressions are the structural rules, which generalize the conventional rules, we need a more general form for the unfolding lemma. The generalization of the lemma is necessary for the type preservation proof with the structural folding/unfolding rules. We call the new lemma the structural unfolding lemma:
Lemma 3.6 (Structural unfolding lemma). If
![]() $\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{B} $
, then
$\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{B} $
, then
![]() $\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}] ~B$
.
$\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}] ~B$
.
In this lemma, in the one-step unfolding the recursive types substituted in the bodies are, respectively, a supertype and a subtype of
![]() ${\mu{\alpha}}.{A}$
and
${\mu{\alpha}}.{A}$
and
![]() ${\mu{\alpha}}.{B}$
. In contrast, in the unfolding lemma proposed by Zhou et al. (Reference Zhou, Oliveira and Fan2022), the recursive types that get substituted in the bodies are the same. As Sections 4.1 and 5.3 will discuss, both forms of the unfolding lemma can be proved using a more general lemma.
${\mu{\alpha}}.{B}$
. In contrast, in the unfolding lemma proposed by Zhou et al. (Reference Zhou, Oliveira and Fan2022), the recursive types that get substituted in the bodies are the same. As Sections 4.1 and 5.3 will discuss, both forms of the unfolding lemma can be proved using a more general lemma.
Type Soundness
To see how the structural unfolding lemma is used in the proof of type preservation, let us consider the typing derivation of an expression
![]() $\textsf{unfold}~[D']~(\textsf{fold}~[C']~e)$
in Figure 4. Starting from a closed expression, both C’ and D’ must be recursive types; thus, we assume that C’ is
$\textsf{unfold}~[D']~(\textsf{fold}~[C']~e)$
in Figure 4. Starting from a closed expression, both C’ and D’ must be recursive types; thus, we assume that C’ is
![]() ${\mu{\alpha}}.{C}$
and D’ is
${\mu{\alpha}}.{C}$
and D’ is
![]() ${\mu{\alpha}}.{D}$
. The type of
${\mu{\alpha}}.{D}$
. The type of
![]() $\textsf{unfold}~[D']~(\textsf{fold}~[C']~e)$
becomes
$\textsf{unfold}~[D']~(\textsf{fold}~[C']~e)$
becomes
![]() $[\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
, and it should be a subtype of
$[\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
, and it should be a subtype of
![]() $[\alpha \mapsto {\mu{\alpha}}.{C} ] ~A$
, which is the type of reduction result e.
$[\alpha \mapsto {\mu{\alpha}}.{C} ] ~A$
, which is the type of reduction result e.

Fig. 4. Structural unfolding derivation.
The other parts of the type soundness proof are standard; thus, we have:
Theorem 3.7 (Preservation). If
![]() $ \vdash e : A $
and
$ \vdash e : A $
and
![]() $e \hookrightarrow e'$
, then
$e \hookrightarrow e'$
, then
![]() $ \vdash e' : A$
.
$ \vdash e' : A$
.
Theorem 3.8 (Progress). If
![]() $\vdash e : A $
, then e is a value or
$\vdash e : A $
, then e is a value or
![]() $e \hookrightarrow e'$
for some e’.
$e \hookrightarrow e'$
for some e’.
3.4 Algorithmic typing
The rules that we have presented in Figure 3 are declarative. The conclusion of the subsumption rule overlaps with all other rules, making it nontrivial to derive an implementation from the rules.
Figure 5 shows the algorithmic rules for typing. Compared with the declarative typing rules, the subsumption rule (typing-sub) is removed. Also, the application (typing-app), type application (typing-tapp), structural folding (typing-sfold), structural unfolding (typing-sunfold), and record projection (typing-proj) rules are replaced by rules atyp-app, atyp-tapp, atyp-sfold atyp-sunfold, and atyp-proj, respectively. In the algorithmic typing rules, we take the standard approach of distributing subtyping checks in appropriate places in the other rules, thus eliminating the need for the subsumption rule.

Fig. 5. Algorithmic typing.
One interesting point is the two exposure relations
![]() $\Uparrow$
and
$\Uparrow$
and
![]() $\Downarrow$
in
$\Downarrow$
in
![]() $F_{\le}^{\mu}$
. In
$F_{\le}^{\mu}$
. In
![]() $F_{\le}$
, there is only the upper exposure function (
$F_{\le}$
, there is only the upper exposure function (
![]() $\Gamma\vdash A \Uparrow B$
), which is used to find the least non-variable upper bound for a variable in the context (Pierce, Reference Pierce2002). Consider the term
$\Gamma\vdash A \Uparrow B$
), which is used to find the least non-variable upper bound for a variable in the context (Pierce, Reference Pierce2002). Consider the term
Without the upper exposure function in the rule atyp-tapp, the y in the function body would be typed as its minimal type
![]() $\alpha$
, which cannot be unified with a function type with the argument type
$\alpha$
, which cannot be unified with a function type with the argument type
![]() $\textsf{nat}$
. The exposure function finds the smallest type that matches the expected type, such as the function type for the argument y in the example above. Thus, the upper exposure function plays an important role in finding the minimal type with the algorithmic typing rules. To make our rules more general, we additionally define the lower exposure function (
$\textsf{nat}$
. The exposure function finds the smallest type that matches the expected type, such as the function type for the argument y in the example above. Thus, the upper exposure function plays an important role in finding the minimal type with the algorithmic typing rules. To make our rules more general, we additionally define the lower exposure function (
![]() $\Gamma \vdash A \Downarrow B$
) to find the greatest non-variable subtype B for A. For
$\Gamma \vdash A \Downarrow B$
) to find the greatest non-variable subtype B for A. For
![]() $F_{\le}^{\mu}$
, lower exposure only helps to find the correct shape for the recursive type body to be folded in rule atyp-sfold by mapping
$F_{\le}^{\mu}$
, lower exposure only helps to find the correct shape for the recursive type body to be folded in rule atyp-sfold by mapping
![]() $\top$
to
$\top$
to
![]() ${\mu{\alpha}}.{\top}$
so that it is valid to type check expressions accepted by the structural rule typing-sfold like
${\mu{\alpha}}.{\top}$
so that it is valid to type check expressions accepted by the structural rule typing-sfold like
with the algorithmic typing rules. The lower exposure function will be more useful when we have lower bounded variables in the system, as we will see in Section 5.
The algorithmic rules are equivalent (sound and complete) with respect to the declarative rules:
Theorem 3.9 (Soundness of the algorithmic rules). If
![]() $\Gamma \vdash_a e : A $
, then
$\Gamma \vdash_a e : A $
, then
![]() $\Gamma \vdash e : A $
.
$\Gamma \vdash e : A $
.
Theorem 3.10 (Completeness of the algorithmic rules). If
![]() $\Gamma \vdash e : A $
, then there exists a B such that
$\Gamma \vdash e : A $
, then there exists a B such that
![]() $\Gamma \vdash_a e : B $
and
$\Gamma \vdash_a e : B $
and
![]() $\Gamma \vdash B \le A$
.
$\Gamma \vdash B \le A$
.
Theorem 3.10 implies that our algorithm can always find a minimal type, which is an important property for
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
It should be noted that there is no difference in terms of algorithmic typing rules for both variants of
![]() $F_{\le}^{\mu}$
, though for full
$F_{\le}^{\mu}$
, though for full
![]() $F_{\le}^{\mu}$
, the algorithm might not terminate, since subtyping is undecidable for
$F_{\le}^{\mu}$
, the algorithm might not terminate, since subtyping is undecidable for
![]() $\textrm{full}~F_{\le}^{\mu}$
.
$\textrm{full}~F_{\le}^{\mu}$
.
4 Metatheory of
 $F_{\le}^{\mu}$
$F_{\le}^{\mu}$
In this section, we discuss the most interesting and difficult aspects of the metatheory of
![]() $F_{\le}^{\mu}$
in more detail. We cover three key properties: the unfolding lemma for
$F_{\le}^{\mu}$
in more detail. We cover three key properties: the unfolding lemma for
![]() $F_{\le}^{\mu}$
, the conservativity of
$F_{\le}^{\mu}$
, the conservativity of
![]() $F_{\le}^{\mu}$
over the original
$F_{\le}^{\mu}$
over the original
![]() $F_\le$
, and (un)decidability of subtyping. The interaction between iso-recursive types and bounded quantification requires significant changes in the proofs of the unfolding lemma and decidability. In addition, we show how to prove the conservativity of
$F_\le$
, and (un)decidability of subtyping. The interaction between iso-recursive types and bounded quantification requires significant changes in the proofs of the unfolding lemma and decidability. In addition, we show how to prove the conservativity of
![]() $F_{\le}^{\mu}$
over
$F_{\le}^{\mu}$
over
![]() $F_\le$
using the algorithmic formulation of
$F_\le$
using the algorithmic formulation of
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
4.1 Unfolding lemma
The unfolding lemma (Lemma 3.5) is a core lemma for the metatheory of a calculus with iso-recursive subtyping. Though the statement of the unfolding lemma is quite simple and intuitive to understand, the lemma cannot be proved directly. We will first review previous approaches for proving the unfolding lemma, which do not account for bounded quantification or only apply to
![]() $\textrm{kernel}~F_{\le}^{\mu}$
. Then we show how to generalize the unfolding lemma to address all the complications arising from the interaction of iso-recursive subtyping and bounded quantification, including the case of
$\textrm{kernel}~F_{\le}^{\mu}$
. Then we show how to generalize the unfolding lemma to address all the complications arising from the interaction of iso-recursive subtyping and bounded quantification, including the case of
![]() $\textrm{full}~F_{\le}^{\mu}$
.
$\textrm{full}~F_{\le}^{\mu}$
.
The Generalized Unfolding Lemma for Iso-Recursive Subtyping
We first review the unfolding lemma for the special case of iso-recursive subtyping without bounded quantification. Because the premise of the unfolding lemma is restricted to a subtyping relation between two recursive types
![]() ${\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
instead of two generic types A and B, a direct induction on the premise is problematic, as it fails to provide a useful induction hypothesis for reasoning with nominal unfoldings like
${\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
instead of two generic types A and B, a direct induction on the premise is problematic, as it fails to provide a useful induction hypothesis for reasoning with nominal unfoldings like ![]() , where the type after substitution may not be a recursive type. In Zhou et al. (Reference Zhou, Oliveira and Fan2022)’s work, the unfolding lemma is generalized to the following form:
, where the type after substitution may not be a recursive type. In Zhou et al. (Reference Zhou, Oliveira and Fan2022)’s work, the unfolding lemma is generalized to the following form:
Lemma 4.1 (The generalized unfolding lemma in Zhou et al., Reference Zhou, Oliveira and Fan2022). If
![]() $\Gamma_1, \alpha, \Gamma_2, \vdash A \le B$
and
$\Gamma_1, \alpha, \Gamma_2, \vdash A \le B$
and
![]() $\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, then
$\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, then
-
1.
 implies
implies
 $\Gamma_1, \Gamma_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B $
;
$\Gamma_1, \Gamma_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B $
; -
2.
 implies
implies
 $\Gamma_1, \Gamma_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]~A \le [\alpha \mapsto {\mu{\alpha}}.{C}]~B $
.
$\Gamma_1, \Gamma_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]~A \le [\alpha \mapsto {\mu{\alpha}}.{C}]~B $
.
Due to the tricky interaction between rule S-var and S-arrow, in the generalized unfolding lemma we need two mutually dependent lemmas: one for covariant cases (1) and the other for contravariant cases (2). The proof for Lemma 4.1 proceeds by induction on
![]() $\Gamma_1, \alpha, \Gamma_2, \vdash A \le B$
. In the inductive proof, we need to switch between covariance and contravariance. In particular, in the rule S-arrow case for functions, we need an induction hypothesis that arises from conclusion (2) to prove the contravariant premise
$\Gamma_1, \alpha, \Gamma_2, \vdash A \le B$
. In the inductive proof, we need to switch between covariance and contravariance. In particular, in the rule S-arrow case for functions, we need an induction hypothesis that arises from conclusion (2) to prove the contravariant premise
![]() $\Gamma \vdash B_1 \le A_1$
relating the input types of the function.
$\Gamma \vdash B_1 \le A_1$
relating the input types of the function.
The Generalized Unfolding Lemma for
 $\textrm{kernel}~F_{\le}^{\mu}$
$\textrm{kernel}~F_{\le}^{\mu}$
When bounded quantification is taken into account, Lemma 4.1 is unfortunately not general enough. The key difference is that now the contexts are no longer just a list of type variables but also associate a type bound with each type variable. Moreover, the bounds are dependent on the type variables in the order they appear so that in the context
![]() $\Gamma_2$
, the bounds may contain the type variable
$\Gamma_2$
, the bounds may contain the type variable
![]() $\alpha$
. Since rule S-vartrans may look up a bound in the context
$\alpha$
. Since rule S-vartrans may look up a bound in the context
![]() $\Gamma_2$
, and compare it with the right-hand side of the subtyping relation, to apply the induction hypothesis, the bound type in the context should be equal to the substitution form
$\Gamma_2$
, and compare it with the right-hand side of the subtyping relation, to apply the induction hypothesis, the bound type in the context should be equal to the substitution form ![]() as in the subtyping relation. To address this issue, Zhou et al. (Reference Zhou, Zhou and Oliveira2023) extend the unfolding lemma to the following form:
as in the subtyping relation. To address this issue, Zhou et al. (Reference Zhou, Zhou and Oliveira2023) extend the unfolding lemma to the following form:
Lemma 4.2 (The generalized unfolding lemma for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
in Zhou et al., Reference Zhou, Zhou and Oliveira2023). If (1)
$\textrm{kernel}~F_{\le}^{\mu}$
in Zhou et al., Reference Zhou, Zhou and Oliveira2023). If (1)
![]() $\Gamma_1,~ \alpha \le \top,~ \Gamma_2 \vdash A \le B$
, (2)
$\Gamma_1,~ \alpha \le \top,~ \Gamma_2 \vdash A \le B$
, (2)
![]() $\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{S}$
and (3)
$\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{S}$
and (3)
![]() $\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{D}$
then
$\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{D}$
then
-
1.
 implies
implies
 $\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
;
$\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
; -
2.
 implies
implies
 $\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{C} ]~B$
.
$\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{C} ]~B$
.
We explain a few key points in the proof of Lemma 4.2 together with some proof sketches below.
Firstly, the context
![]() $\Gamma_2$
now comes with a substitution. Here, the syntax
$\Gamma_2$
now comes with a substitution. Here, the syntax
![]() $\Gamma[\alpha \mapsto S]$
denotes that all the occurrences of
$\Gamma[\alpha \mapsto S]$
denotes that all the occurrences of
![]() $\alpha$
in context
$\alpha$
in context
![]() $\Gamma$
will be replaced by a specified type S. With substitutions in the context
$\Gamma$
will be replaced by a specified type S. With substitutions in the context
![]() $\Gamma_2$
, in case S-vartrans,S-equivall, the premise from inversion can have the same form as the original premise and thus the induction hypothesis can be applied. For example, in case S-vartrans, assume that
$\Gamma_2$
, in case S-vartrans,S-equivall, the premise from inversion can have the same form as the original premise and thus the induction hypothesis can be applied. For example, in case S-vartrans, assume that
![]() $A:=\beta$
,
$A:=\beta$
,
![]() $B:=B$
, and
$B:=B$
, and
![]() $\Gamma_2$
contains a bound
$\Gamma_2$
contains a bound
![]() $\beta \le U$
. We need to prove the following goal:
$\beta \le U$
. We need to prove the following goal:
By analyzing the context we know that
![]() $\beta \le [\alpha \mapsto {\mu{\alpha}}.{S}]~U \in \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ]$
, so we only need to show
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{S}]~U \in \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ]$
, so we only need to show
This can be proved by instantiating the induction hypothesis with
![]() $C:=S$
and
$C:=S$
and
![]() $D:=D$
. In this way, we overcome the issue with the substitutions in the context
$D:=D$
. In this way, we overcome the issue with the substitutions in the context
![]() $\Gamma_2$
.
$\Gamma_2$
.
Second, note that the substituted type is neither C nor D, but an intermediate type S that lies between C and D. This is to ensure that the induction hypothesis can be applied to both the contravariant and covariant subgoals in case S-arrow. Otherwise, consider an alternative lemma where S is fixed to be D. In case S-arrow, assume that
![]() $A:=A_1 \to A_2$
and
$A:=A_1 \to A_2$
and
![]() $B:=B_1 \to B_2$
. We need to prove two subgoals:
$B:=B_1 \to B_2$
. We need to prove two subgoals:
-
1.
 $\Gamma_1, \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{D} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A_2 \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B_2 $
$\Gamma_1, \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{D} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A_2 \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B_2 $
-
2.
 $\Gamma_1, \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{D} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]~B_1 \le [\alpha \mapsto {\mu{\alpha}}.{C}]~A_1 $
$\Gamma_1, \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{D} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]~B_1 \le [\alpha \mapsto {\mu{\alpha}}.{C}]~A_1 $
If one follows the original proof steps in Lemma 4.1, the induction hypothesis has to be instantiated with
![]() $C:=D$
and
$C:=D$
and
![]() $D:=C$
so that the substitution matches with the two types in the subtyping relation for the contravariant subgoal (2). In that case, the substituted type in the context
$D:=C$
so that the substitution matches with the two types in the subtyping relation for the contravariant subgoal (2). In that case, the substituted type in the context
![]() $\Gamma_2$
becomes
$\Gamma_2$
becomes
![]() ${\mu{\alpha}}.{C}$
, which cannot be used to prove the subgoal (2). Therefore, in Lemma 4.2 an intermediate type S is introduced to decouple the substitution in the context and in the subtyping relation for the function case. In other words, the invariant substitution with type
${\mu{\alpha}}.{C}$
, which cannot be used to prove the subgoal (2). Therefore, in Lemma 4.2 an intermediate type S is introduced to decouple the substitution in the context and in the subtyping relation for the function case. In other words, the invariant substitution with type
![]() ${\mu{\alpha}}.{S}$
to the context makes the induction hypothesis applicable to both subgoals, regardless of the substitution in the subtyping relation.
${\mu{\alpha}}.{S}$
to the context makes the induction hypothesis applicable to both subgoals, regardless of the substitution in the subtyping relation.
Finally, having the intermediate type S will not affect the inductive proof for case S-equivall in
![]() $\textrm{kernel}~F_{\le}^{\mu}$
. We assume that
$\textrm{kernel}~F_{\le}^{\mu}$
. We assume that
![]() $A:=\forall({\beta}\le{A_1}).{A_2}$
and
$A:=\forall({\beta}\le{A_1}).{A_2}$
and
![]() $B:=\forall({\beta}\le{B_1}).{B_2}$
. The goal would look like:
$B:=\forall({\beta}\le{B_1}).{B_2}$
. The goal would look like:
After simplification and applying rule S-equivall, one of the goals becomes:
To apply the induction hypothesis, we need to unify the new bound
![]() $\beta \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B_1$
and the existing context
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{D}]~B_1$
and the existing context
![]() $\Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ]$
into the same substitution form. In other words, we need to show the following two environments are equivalent:
$\Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ]$
into the same substitution form. In other words, we need to show the following two environments are equivalent:
This can be done by showing that
![]() ${\mu{\alpha}}.{S}$
is equivalent to
${\mu{\alpha}}.{S}$
is equivalent to
![]() ${\mu{\alpha}}.{D}$
. To prove this, we rely on the fact that the bounds
${\mu{\alpha}}.{D}$
. To prove this, we rely on the fact that the bounds ![]() and
and ![]() are equivalent, and the following inversion lemma on substitution:
are equivalent, and the following inversion lemma on substitution:
Lemma 4.3 (Substitution inversion). If A is equivalent to B, and ![]() is equivalent to
is equivalent to ![]() , then either C is equivalent to D or
, then either C is equivalent to D or
![]() $\alpha$
is not in A nor B.
$\alpha$
is not in A nor B.
For the first case we get from Lemma 4.3, by the fact that S lies in the middle of C and D, we can show that all the three types
![]() ${\mu{\alpha}}.{C}$
,
${\mu{\alpha}}.{C}$
,
![]() ${\mu{\alpha}}.{S}$
, and
${\mu{\alpha}}.{S}$
, and
![]() ${\mu{\alpha}}.{D}$
are equivalent. For the second case, since
${\mu{\alpha}}.{D}$
are equivalent. For the second case, since
![]() $\alpha$
is not in
$\alpha$
is not in
![]() $A_1$
nor
$A_1$
nor
![]() $A_2$
, we can freely rewrite the substituted types to any types in the context. In either case, the rewriting in (4.1) can be achieved, so that the induction hypothesis can be applied to the subgoal. The critical point here is that, although the substitution form in the context is indeed affected by the new bound introduced by rule S-equivall, since
$A_2$
, we can freely rewrite the substituted types to any types in the context. In either case, the rewriting in (4.1) can be achieved, so that the induction hypothesis can be applied to the subgoal. The critical point here is that, although the substitution form in the context is indeed affected by the new bound introduced by rule S-equivall, since
![]() $\textrm{kernel}~F_{\le}^{\mu}$
requires all pairs of the bounds in the subtyping relation to be equivalent, the type S will converge into the types C and D in the end.
$\textrm{kernel}~F_{\le}^{\mu}$
requires all pairs of the bounds in the subtyping relation to be equivalent, the type S will converge into the types C and D in the end.
The Generalized Unfolding Lemma for Kernel
 $F_{\le\ge}^{\mu}$
$F_{\le\ge}^{\mu}$
In Zhou et al. (Reference Zhou, Zhou and Oliveira2023)’s work, an extension to
![]() $\textrm{kernel}~F_{\le}^{\mu}$
is proposed, called
$\textrm{kernel}~F_{\le}^{\mu}$
is proposed, called
![]() $F_{\le\ge}^{\mu}$
, which extends
$F_{\le\ge}^{\mu}$
, which extends
![]() $\textrm{kernel}~F_{\le}^{\mu}$
with lower bounded quantification and bottom types. It is worth noting that these new features will break the proof of Lemma 4.2 we have discussed above. The interaction of lower bounds and upper bounds invalidates the following inversion lemma for S-vartrans, which has been used to prove Lemma 4.2:
$\textrm{kernel}~F_{\le}^{\mu}$
with lower bounded quantification and bottom types. It is worth noting that these new features will break the proof of Lemma 4.2 we have discussed above. The interaction of lower bounds and upper bounds invalidates the following inversion lemma for S-vartrans, which has been used to prove Lemma 4.2:
Lemma 4.4 If
![]() $\alpha \le A \in \Gamma$
and
$\alpha \le A \in \Gamma$
and
![]() $\Gamma \vdash \alpha \le B$
, where
$\Gamma \vdash \alpha \le B$
, where
![]() $\alpha \neq B$
, then
$\alpha \neq B$
, then
![]() $\Gamma \vdash A \le B$
.
$\Gamma \vdash A \le B$
.
In Lemma 4.2, there is more than one subtyping statement on the premises related to type A and B. During the proof we do induction on the premise (1), and use the inversion lemma to match the subderivation of ![]() with the induction hypothesis we get from the premise (1). Lemma 4.4 holds when the bounds in the context can only have one direction. However, when we have both kinds of bounds in the context, a counterexample can be found as follows:
with the induction hypothesis we get from the premise (1). Lemma 4.4 holds when the bounds in the context can only have one direction. However, when we have both kinds of bounds in the context, a counterexample can be found as follows:
To avoid using this inversion lemma in the proof of unfolding lemma, we need to refine the generalized unfolding lemma for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
:
$\textrm{kernel}~F_{\le}^{\mu}$
:
Lemma 4.5 (The generalized unfolding lemma for
![]() $F_{\le\ge}^{\mu}$
in Zhou et al. Reference Zhou, Zhou and Oliveira2023). If
$F_{\le\ge}^{\mu}$
in Zhou et al. Reference Zhou, Zhou and Oliveira2023). If
-
1.
 $\Gamma_1,~\alpha \le \top,~\Gamma_2 \vdash A$
and
$\Gamma_1,~\alpha \le \top,~\Gamma_2 \vdash A$
and
 $\Gamma_1,~\alpha \le \top,~\Gamma_2 \vdash B$
;
$\Gamma_1,~\alpha \le \top,~\Gamma_2 \vdash B$
; -
2.
 ;
; -
3. G differs from
 only in the components labeled by
only in the components labeled by  , where
, where  can be replaced by
can be replaced by  that satisfies
that satisfies
 $\Gamma_2 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{T}$
and
$\Gamma_2 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{T}$
and
 $\Gamma_2 \vdash {\mu{\alpha}}.{T} \le {\mu{\alpha}}.{S}$
,
$\Gamma_2 \vdash {\mu{\alpha}}.{T} \le {\mu{\alpha}}.{S}$
,
then
-
1.
 $\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{S}$
and
$\Gamma_1 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{S}$
and
 $\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{D}$
implies
$\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{D}$
implies
 $\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
;
$\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
; -
2.
 $\Gamma_1 \vdash {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{S}$
and
$\Gamma_1 \vdash {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{S}$
and
 $\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{C}$
implies
$\Gamma_1 \vdash {\mu{\alpha}}.{S} \le {\mu{\alpha}}.{C}$
implies
 $\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
.
$\Gamma_1,~ \Gamma_2[\alpha \mapsto {\mu{\alpha}}.{S} ] \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ]~A \le [\alpha \mapsto {\mu{\alpha}}.{D} ]~B$
.
In the refined generalized unfolding lemma, we integrate the two subtyping statements into one statement, by having the premise (1) in Lemma 4.2 induced implicitly. This can be justified by the fact that the one-time unfolding is implicitly derived from the nominal unfolding:
Lemma 4.6 (Inversion on nominal unfoldings). If ![]() , then
, then
![]() $\Gamma \vdash A \le B$
.
$\Gamma \vdash A \le B$
.
To accommodate this change, the context is also refined to be more general, by allowing the substitution type in the subtyping context of premise (2) to be any type T equivalent to S. We omit the detailed proof for this lemma, since it was done in the appendix of Zhou et al. (Reference Zhou, Zhou and Oliveira2023) and is no longer used in the generalized unfolding lemma for
![]() $\textrm{full}~F_{\le}^{\mu}$
and
$\textrm{full}~F_{\le}^{\mu}$
and
![]() $F_{\le\ge}^{\mu\wedge}$
we will present in this paper. However, the idea of using Lemma 4.6 to avoid the issue of using Lemma 4.4 still applies, as we will show next.
$F_{\le\ge}^{\mu\wedge}$
we will present in this paper. However, the idea of using Lemma 4.6 to avoid the issue of using Lemma 4.4 still applies, as we will show next.
The Generalized Unfolding Lemma for
 $\textrm{full}~F_{\le}^{\mu}$
$\textrm{full}~F_{\le}^{\mu}$
It is not straightforward to generalize the unfolding lemma to
![]() $\textrm{full}~F_{\le}^{\mu}$
. As we have seen in the last observation of Lemma 4.2, the proof relies on the fact that the bounds in the subtyping relation are equivalent, so that during the proof, the intermediate type
$\textrm{full}~F_{\le}^{\mu}$
. As we have seen in the last observation of Lemma 4.2, the proof relies on the fact that the bounds in the subtyping relation are equivalent, so that during the proof, the intermediate type
![]() ${\mu{\alpha}}.{S}$
can be rewritten to
${\mu{\alpha}}.{S}$
can be rewritten to
![]() ${\mu{\alpha}}.{C}$
or
${\mu{\alpha}}.{C}$
or
![]() ${\mu{\alpha}}.{D}$
. However, in
${\mu{\alpha}}.{D}$
. However, in
![]() $\textrm{full}~F_{\le}^{\mu}$
we use rule S-fullall, which fails to maintain the equivalence of the bounds. We need to consider a new approach to generalize the unfolding lemma for
$\textrm{full}~F_{\le}^{\mu}$
we use rule S-fullall, which fails to maintain the equivalence of the bounds. We need to consider a new approach to generalize the unfolding lemma for
![]() $\textrm{full}~F_{\le}^{\mu}$
.
$\textrm{full}~F_{\le}^{\mu}$
.
If we revisit the use of the generalized substitution type S in the context
![]() $\Gamma_2$
in Lemma 4.2, we can see that, during the proof, in most cases we just pass the same type S around in the induction hypothesis. The exception is for the case of S-vartrans, where the type S is instantiated to C or D. This suggests that the issues with the unfolding lemma in
$\Gamma_2$
in Lemma 4.2, we can see that, during the proof, in most cases we just pass the same type S around in the induction hypothesis. The exception is for the case of S-vartrans, where the type S is instantiated to C or D. This suggests that the issues with the unfolding lemma in
![]() $\textrm{full}~F_{\le}^{\mu}$
can be solved if we can find a different approach to the S-vartrans case and remove the intermediate type S from the generalized unfolding lemma. In that case, the requirement for the equivalent bounds can also be lifted.
$\textrm{full}~F_{\le}^{\mu}$
can be solved if we can find a different approach to the S-vartrans case and remove the intermediate type S from the generalized unfolding lemma. In that case, the requirement for the equivalent bounds can also be lifted.
To this end, we note that the introduction of the type S in Lemma 4.2 is essentially an over-generalization, since throughout the derivation of ![]() , only the substitution C or D will be introduced into the context. Thus, the generalized unfolding lemma can focus only on the substitution of C or D. However, in
, only the substitution C or D will be introduced into the context. Thus, the generalized unfolding lemma can focus only on the substitution of C or D. However, in
![]() $\textrm{full}~F_{\le}^{\mu}$
, it can happen that we cannot find a uniform substitution type for the variable
$\textrm{full}~F_{\le}^{\mu}$
, it can happen that we cannot find a uniform substitution type for the variable
![]() $\alpha$
in the context
$\alpha$
in the context
![]() $\Gamma_2$
. Due to the contravariant subtyping in rule S-ARROW, the substitutions can flip between the two sides of the subtyping relation, so both C and D can be introduced into the context. Therefore, we define the following notion of related contexts to characterize such contexts:
$\Gamma_2$
. Due to the contravariant subtyping in rule S-ARROW, the substitutions can flip between the two sides of the subtyping relation, so both C and D can be introduced into the context. Therefore, we define the following notion of related contexts to characterize such contexts:
Definition 4.7 (Related contexts). Given a type variable
![]() $\alpha$
, an initial context
$\alpha$
, an initial context
![]() $\Gamma_0$
, and two types
$\Gamma_0$
, and two types
![]() ${\mu{\alpha}}.{C}$
,
${\mu{\alpha}}.{C}$
,
![]() ${\mu{\alpha}}.{D}$
, two contexts
${\mu{\alpha}}.{D}$
, two contexts
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma_\mu$
are related, written
$\Gamma_\mu$
are related, written ![]() , if they can be derived using the following rules:
, if they can be derived using the following rules:

The definition of related contexts is parameterized by a type variable
![]() $\alpha$
and a subtyping relation
$\alpha$
and a subtyping relation
![]() $\Gamma_0 \vdash {\mu{\alpha}}.{C} \le \mu \alpha. ~D$
.Footnote
3
As we will see, the two contexts
$\Gamma_0 \vdash {\mu{\alpha}}.{C} \le \mu \alpha. ~D$
.Footnote
3
As we will see, the two contexts
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma_\mu$
are essentially the subtyping contexts that will be used in the generalized unfolding lemma for the premise and the conclusion, respectively. They extend the context
$\Gamma_\mu$
are essentially the subtyping contexts that will be used in the generalized unfolding lemma for the premise and the conclusion, respectively. They extend the context
![]() $\Gamma_0$
with new bindings that are either under the substitution C or D. Moreover, each pair of bindings in the two contexts should be matched in terms of the substitution type C or D and the base type A should be the same. For example, consider the following instance of the unfolding lemma we aim to prove:
$\Gamma_0$
with new bindings that are either under the substitution C or D. Moreover, each pair of bindings in the two contexts should be matched in terms of the substitution type C or D and the base type A should be the same. For example, consider the following instance of the unfolding lemma we aim to prove:

By definition,
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
are related under the subtyping relation
$\Gamma_2$
are related under the subtyping relation
![]() $\cdot \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, that is,
$\cdot \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, that is, ![]() . When proving the above goal, for the contravariant case of function types, we need to show that the following holds:
. When proving the above goal, for the contravariant case of function types, we need to show that the following holds:

To prove this by induction,
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
should be related under the subtyping relation
$\Gamma_2$
should be related under the subtyping relation
![]() $\cdot \vdash {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{C}$
, which flips the order of
$\cdot \vdash {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{C}$
, which flips the order of
![]() ${\mu{\alpha}}.{C}$
and
${\mu{\alpha}}.{C}$
and
![]() ${\mu{\alpha}}.{D}$
in the parameter of the related contexts. This is possible because the related contexts are defined to be symmetric in terms of the substitution types C and D. This flexibility allows us to prove the generalized unfolding lemma for
${\mu{\alpha}}.{D}$
in the parameter of the related contexts. This is possible because the related contexts are defined to be symmetric in terms of the substitution types C and D. This flexibility allows us to prove the generalized unfolding lemma for
![]() $\textrm{full}~F_{\le}^{\mu}$
without the need for the intermediate type S as in Lemma 4.2 to handle the contravariance.
$\textrm{full}~F_{\le}^{\mu}$
without the need for the intermediate type S as in Lemma 4.2 to handle the contravariance.
With the notion of related contexts, we can prove inversion lemmas for looking up the bounds in the related contexts:
Lemma 4.8 (Inversion lemma for related contexts). If
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma_\mu$
are related under the variable
$\Gamma_\mu$
are related under the variable
![]() $\alpha$
, the shared context
$\alpha$
, the shared context
![]() $\Gamma_0$
, and the types
$\Gamma_0$
, and the types
![]() ${\mu{\alpha}}.{C}$
and
${\mu{\alpha}}.{C}$
and
![]() ${\mu{\alpha}}.{D}$
, then for any type variable
${\mu{\alpha}}.{D}$
, then for any type variable
![]() $\beta$
, if
$\beta$
, if
![]() $\beta \le U \in \Gamma$
and
$\beta \le U \in \Gamma$
and
![]() $\beta \neq \alpha$
, one of the following holds:
$\beta \neq \alpha$
, one of the following holds:
-
1. there exists U’, s.t.
 and
and
 $\beta \le [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \in \Gamma_\mu$
, or
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \in \Gamma_\mu$
, or -
2. there exists U’, s.t.
 and
and
 $\beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \in \Gamma_\mu$
.
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \in \Gamma_\mu$
.
We can now state the generalized unfolding lemma for
![]() $\textrm{full}~F_{\le}^{\mu}$
:
$\textrm{full}~F_{\le}^{\mu}$
:
Lemma 4.9 (The generalized unfolding lemma for
![]() $\textrm{full}~F_{\le}^{\mu}$
). If contexts
$\textrm{full}~F_{\le}^{\mu}$
). If contexts
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma_\mu$
are related under variable
$\Gamma_\mu$
are related under variable
![]() $\alpha$
and if
$\alpha$
and if
![]() $\Gamma_0 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, then
$\Gamma_0 \vdash {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D}$
, then
-
1.
 implies
implies
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]A \le [\alpha \mapsto {\mu{\alpha}}.{D}]B$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]A \le [\alpha \mapsto {\mu{\alpha}}.{D}]B$
-
2.
 implies
implies
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]A \le [\alpha \mapsto {\mu{\alpha}}.{C}]B$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]A \le [\alpha \mapsto {\mu{\alpha}}.{C}]B$
-
3.
 implies
implies
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]A \le [\alpha \mapsto {\mu{\alpha}}.{C}]B$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]A \le [\alpha \mapsto {\mu{\alpha}}.{C}]B$
-
4.
 implies
implies
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]A \le [\alpha \mapsto {\mu{\alpha}}.{D}]B$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D}]A \le [\alpha \mapsto {\mu{\alpha}}.{D}]B$
Compared to previous versions of the unfolding lemma, in addition to conclusion (1) and (2), which talk about the covariant and contravariant substitutions, now we add two more conclusions (3) and (4) for the case where the substitutions are the same as C or D. As we will show in the proof sketch below, these two additional conclusions generate useful induction hypotheses for the proof of rule S-vartrans so that we no longer need to rely on the intermediate type S as we did in Lemma 4.2. Moreover, we follow the same approach as in Lemma 4.9 to drop the premise of
![]() $A \le B$
and avoid the use of inversion lemmas.
$A \le B$
and avoid the use of inversion lemmas.
Proof. We prove the four mutually dependent goals in the lemma by induction on the premise ![]() . We unroll the mutual induction hypothesis here and assume four separate induction hypotheses available in the proof for the sake of presentation. In the rest of the proof, we will refer to them as IH(n) for the induction hypothesis generated by the proof goal (n). We show the interesting cases below:
. We unroll the mutual induction hypothesis here and assume four separate induction hypotheses available in the proof for the sake of presentation. In the rest of the proof, we will refer to them as IH(n) for the induction hypothesis generated by the proof goal (n). We show the interesting cases below:
-
• Rule S-vartrans: We show the proof goal (1) here. Assume
 $A = \beta$
, where
$A = \beta$
, where
 $\beta \le U \in \Gamma$
, and
$\beta \le U \in \Gamma$
, and  , by Lemma 4.8 we get two cases:
, by Lemma 4.8 we get two cases:-
• There exists U’,
 and
and
 $\beta \le [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \in \Gamma_\mu$
. We need to show
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \in \Gamma_\mu$
. We need to show
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B$
. We can apply IH(1) directly.
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] U' \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B$
. We can apply IH(1) directly. -
• There exists U’,
 and
and
 $\beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \in \Gamma_\mu$
. We need to show
$\beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \in \Gamma_\mu$
. We need to show
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B$
. We can apply IH(4) directly. Note that in this case, the substituted type on both sides is D, which motivated us to state cases (3) and (4) in the lemma.
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] U' \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B$
. We can apply IH(4) directly. Note that in this case, the substituted type on both sides is D, which motivated us to state cases (3) and (4) in the lemma.
-
The proof for the other cases is similar to this one, by first applying Lemma 4.8 to get the corresponding cases, and then choosing the induction hypothesis that applies to complete the proof.
-
• Rule S-arrow: Assume
 $A = A_1 \rightarrow A_2$
and
$A = A_1 \rightarrow A_2$
and
 $B = B_1 \rightarrow B_2$
, for proof goal (1), we need to prove two subgoals:
$B = B_1 \rightarrow B_2$
, for proof goal (1), we need to prove two subgoals:-
•
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] B_1 \le [\alpha \mapsto {\mu{\alpha}}.{C} ] A_1$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] B_1 \le [\alpha \mapsto {\mu{\alpha}}.{C} ] A_1$
-
•
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] A_2 \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] A_2 \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2$
-
The covariant subgoal (2) follows from IH(1) directly. In subgoal (1), due to the contravariant subtyping, the substituted types are flipped in the subtyping relation. Therefore, we need to apply IH(2) to complete the proof. The proof of subgoal (2) is similar to the proof of subgoal (1), by applying IH(1) to the contravariant subgoal, and IH(2) to the covariant subgoal. For subgoals (3) and (4), the induction hypothesis can be applied directly since the substituted types are the same on both sides.
-
• Rule S-fullall: Assume
 $A = \forall({\beta}\le{B_1}).{A_1}$
and
$A = \forall({\beta}\le{B_1}).{A_1}$
and
 $B = \forall({\beta}\le{B_2}).{A_2}$
. We show the proof of goal (1) here. In this case, we need to prove two subgoals:
$B = \forall({\beta}\le{B_2}).{A_2}$
. We show the proof of goal (1) here. In this case, we need to prove two subgoals:-
•
 $\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2 \le [\alpha \mapsto {\mu{\alpha}}.{C} ] B_1$
$\Gamma_\mu \vdash [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2 \le [\alpha \mapsto {\mu{\alpha}}.{C} ] B_1$
-
•
 $\Gamma_\mu, \beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] A_1 \le [\alpha \mapsto {\mu{\alpha}}.{D} ] A_2$
$\Gamma_\mu, \beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2 \vdash [\alpha \mapsto {\mu{\alpha}}.{C} ] A_1 \le [\alpha \mapsto {\mu{\alpha}}.{D} ] A_2$
-
The proof of subgoal (1) is similar to the proof of subgoal (1) in the S-arrow case, by applying IH(2) to the contravariant subgoal. Next, in order to apply IH(1) to the covariant subgoal (2), we need to show that the context ![]() and
and
![]() $(\Gamma_\mu, \beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2)$
are related, which follows from the definition of related contexts. Therefore, we can apply IH(1) to complete the proof. The proof of other goals is similar to the proof of goal (1). Thanks to our definition of related contexts, we do not need to worry about whether the substituted type is C or D when we add a new binding into the context in the proof of subgoal (2).
$(\Gamma_\mu, \beta \le [\alpha \mapsto {\mu{\alpha}}.{D} ] B_2)$
are related, which follows from the definition of related contexts. Therefore, we can apply IH(1) to complete the proof. The proof of other goals is similar to the proof of goal (1). Thanks to our definition of related contexts, we do not need to worry about whether the substituted type is C or D when we add a new binding into the context in the proof of subgoal (2).
To conclude, in this generalized unfolding lemma, we introduce two more conclusions for the case where the substitutions are the same as C or D, and we define related contexts to characterize the contexts that will be used in the proof. In this way, we prove the case of rule S-vartrans without the need for an intermediate type S, so that rule S-fullall can be handled as well. In fact, the proof technique we use here is quite general. We also redevelop a generalized unfolding lemma for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
using the same approach as in
$\textrm{kernel}~F_{\le}^{\mu}$
using the same approach as in
![]() $\textrm{full}~F_{\le}^{\mu}$
. As we will see, this generalized unfolding lemma can also be used to prove
$\textrm{full}~F_{\le}^{\mu}$
. As we will see, this generalized unfolding lemma can also be used to prove
![]() $F_{\le\ge}^{\mu\wedge}$
, without the need for significant changes.
$F_{\le\ge}^{\mu\wedge}$
, without the need for significant changes.
4.2 Conservativity
One important feature of
![]() $F_{\le}^{\mu}$
is that it is conservative over
$F_{\le}^{\mu}$
is that it is conservative over
![]() $F_{\le}$
. Conservativity means that equivalent
$F_{\le}$
. Conservativity means that equivalent
![]() $F_{\le}$
judgments in
$F_{\le}$
judgments in
![]() $F_{\le}^{\mu}$
should behave in the same way as in
$F_{\le}^{\mu}$
should behave in the same way as in
![]() $F_{\le}$
. For instance, if a subtyping statement is valid in
$F_{\le}$
. For instance, if a subtyping statement is valid in
![]() $F_{\le}$
, then it should also be valid in
$F_{\le}$
, then it should also be valid in
![]() $F_{\le}^{\mu}$
. Dually, if a subtyping statement over
$F_{\le}^{\mu}$
. Dually, if a subtyping statement over
![]() $F_\le$
-types is invalid in
$F_\le$
-types is invalid in
![]() $F_{\le}$
, then it should also be invalid in
$F_{\le}$
, then it should also be invalid in
![]() $F_{\le}^{\mu}$
. In some calculi, including extensions of
$F_{\le}^{\mu}$
. In some calculi, including extensions of
![]() $F_{\le}$
with equi-recursive types (Ghelli Reference Ghelli1993), conservativity is lost after the addition of new features.
$F_{\le}$
with equi-recursive types (Ghelli Reference Ghelli1993), conservativity is lost after the addition of new features.
To avoid ambiguity, we let
![]() $\vdash_F \Gamma$
be the well-formedness of environment,
$\vdash_F \Gamma$
be the well-formedness of environment,
![]() $\Gamma \vdash_F A$
be the well-formedness of types,
$\Gamma \vdash_F A$
be the well-formedness of types,
![]() $\Gamma \vdash_F A \le B$
be the subtyping relation,
$\Gamma \vdash_F A \le B$
be the subtyping relation,
![]() $\vdash_F e$
be the well-formedness of expressions, and
$\vdash_F e$
be the well-formedness of expressions, and
![]() $\Gamma \vdash_F e : A$
be the typing relation in
$\Gamma \vdash_F e : A$
be the typing relation in
![]() $F_{\le}$
, where the subscript F stands for the original
$F_{\le}$
, where the subscript F stands for the original
![]() $F_{\le}$
calculus. All the definitions and rules for
$F_{\le}$
calculus. All the definitions and rules for
![]() $F_{\le}$
are essentially subsets of the corresponding definitions and rules for
$F_{\le}$
are essentially subsets of the corresponding definitions and rules for
![]() $F_{\le}^{\mu}$
presented in Section 3, except that the rules involving records and recursive types are removed, and that in
$F_{\le}^{\mu}$
presented in Section 3, except that the rules involving records and recursive types are removed, and that in
![]() $\textrm{kernel}~F_{\le}$
, the rule S-equivall is replaced with the rule S-kernelall. Note that the properties we will show below in this section are demonstrated in both variants of
$\textrm{kernel}~F_{\le}$
, the rule S-equivall is replaced with the rule S-kernelall. Note that the properties we will show below in this section are demonstrated in both variants of
![]() $F_{\le}^{\mu}$
. In other words,
$F_{\le}^{\mu}$
. In other words,
![]() $\textrm{full}~F_{\le}^{\mu}$
is conservative over
$\textrm{full}~F_{\le}^{\mu}$
is conservative over
![]() $\textrm{full}~F_{\le}$
and
$\textrm{full}~F_{\le}$
and
![]() $\textrm{kernel}~F_{\le}^{\mu}$
is conservative over
$\textrm{kernel}~F_{\le}^{\mu}$
is conservative over
![]() $\textrm{kernel}~F_{\le}$
.
$\textrm{kernel}~F_{\le}$
.
Conservativity of Subtyping
Our conservativity result for subtyping is relatively easy to establish:
Lemma 4.10 (Conservativity for subtyping). If
![]() $\Gamma$
, A, and B are well formed in
$\Gamma$
, A, and B are well formed in
![]() $F_{\le}$
, namely (1)
$F_{\le}$
, namely (1)
![]() $\vdash_F \Gamma$
, (2)
$\vdash_F \Gamma$
, (2)
![]() $\Gamma \vdash_F A$
, and (3)
$\Gamma \vdash_F A$
, and (3)
![]() $\Gamma \vdash_F B$
, then
$\Gamma \vdash_F B$
, then
![]() $\Gamma \vdash_F A \le B$
if and only if
$\Gamma \vdash_F A \le B$
if and only if
![]() $\Gamma \vdash A \le B$
.
$\Gamma \vdash A \le B$
.
Here, the well-formedness conditions ensure that
![]() $\Gamma$
, A, and B must be respectively a valid
$\Gamma$
, A, and B must be respectively a valid
![]() $F_\le$
environment, and valid
$F_\le$
environment, and valid
![]() $F_\le$
types. That is they cannot contain recursive types (or record types). Therefore, the lemma states that for environments and types without recursive types, the two subtyping relations (for
$F_\le$
types. That is they cannot contain recursive types (or record types). Therefore, the lemma states that for environments and types without recursive types, the two subtyping relations (for
![]() $F_\le$
and
$F_\le$
and
![]() $F_{\le}^{\mu}$
) are equivalent, accepting the same statements.
$F_{\le}^{\mu}$
) are equivalent, accepting the same statements.
The proof of this lemma is straightforward, except for the case of rule S-equivall from
![]() $F_{\le}^{\mu}$
to
$F_{\le}^{\mu}$
to
![]() $F_{\le}$
, as the rule S-kernelall in
$F_{\le}$
, as the rule S-kernelall in
![]() $F_{\le}$
requires the two types to be exactly the same instead of being equivalent. This is easy to fix, given that
$F_{\le}$
requires the two types to be exactly the same instead of being equivalent. This is easy to fix, given that
![]() $\textrm{kernel}~F_{\le}$
subtyping is antisymmetric. This property was shown by Baldan et al. (Reference Baldan, Ghelli and Raffaetà1999) for a restricted form of F-bounded quantification, and we adapt their proof to our setting. The antisymmetry property is stated as follows:
$\textrm{kernel}~F_{\le}$
subtyping is antisymmetric. This property was shown by Baldan et al. (Reference Baldan, Ghelli and Raffaetà1999) for a restricted form of F-bounded quantification, and we adapt their proof to our setting. The antisymmetry property is stated as follows:
Lemma 4.11 (Antisymmetry of
![]() $\textrm{kernel}~F_{\le}$
subtyping). If
$\textrm{kernel}~F_{\le}$
subtyping). If
![]() $\Gamma \vdash_F A \le B$
and
$\Gamma \vdash_F A \le B$
and
![]() $\Gamma \vdash_F B \le A$
in
$\Gamma \vdash_F B \le A$
in
![]() $\textrm{kernel}~F_{\le}$
, then
$\textrm{kernel}~F_{\le}$
, then
![]() $A = B$
.
$A = B$
.
Conservativity of Typing
It is straightforward to obtain one direction of the conservativity result, from a typing relation in
![]() $F_{\le}$
to a typing relation in
$F_{\le}$
to a typing relation in
![]() $F_{\le}^{\mu}$
. As for the reverse direction, the situation is more complicated. If we want to derive
$F_{\le}^{\mu}$
. As for the reverse direction, the situation is more complicated. If we want to derive
![]() $\Gamma \vdash_F e : A $
from
$\Gamma \vdash_F e : A $
from
![]() $\Gamma \vdash e : A $
, when doing induction, for the subsumption case (rule typing-sub), we need to guess an intermediate type. However, we do not know if it involves recursive types or not. Consider the following example:
$\Gamma \vdash e : A $
, when doing induction, for the subsumption case (rule typing-sub), we need to guess an intermediate type. However, we do not know if it involves recursive types or not. Consider the following example:

Although the final judgment
![]() $\vdash \lambda x.~x : \top$
does not involve recursive types, the typing subderivations can contain recursive types. As a result, the induction hypothesis cannot be applied.
$\vdash \lambda x.~x : \top$
does not involve recursive types, the typing subderivations can contain recursive types. As a result, the induction hypothesis cannot be applied.
This problem can be addressed by employing the algorithmic formulation of
![]() $F_{\le}^{\mu}$
, shown in Section 3.4. With algorithmic typing, we can have more precise information about the types of an expression, since algorithmic typing always gives the minimum type. Therefore, it can be proved that, for expressions that do not use fold/unfold constructors, their minimum types do not contain recursive types either. We state this property as the conservativity lemma for subtyping:
$F_{\le}^{\mu}$
, shown in Section 3.4. With algorithmic typing, we can have more precise information about the types of an expression, since algorithmic typing always gives the minimum type. Therefore, it can be proved that, for expressions that do not use fold/unfold constructors, their minimum types do not contain recursive types either. We state this property as the conservativity lemma for subtyping:
Lemma 4.12. If
![]() $\Gamma$
, A, and e are well formed in
$\Gamma$
, A, and e are well formed in
![]() $F_{\le}$
, namely (1)
$F_{\le}$
, namely (1)
![]() $\vdash_F \Gamma$
, (2)
$\vdash_F \Gamma$
, (2)
![]() $\Gamma \vdash_F A$
, and (3)
$\Gamma \vdash_F A$
, and (3)
![]() $\vdash_F e$
, then
$\vdash_F e$
, then
![]() $\Gamma \vdash_a e:A$
implies
$\Gamma \vdash_a e:A$
implies
![]() $\Gamma \vdash_F e : A$
.
$\Gamma \vdash_F e : A$
.
Now, given a typing relation
![]() $\Gamma \vdash e:A$
in
$\Gamma \vdash e:A$
in
![]() $F_{\le}^{\mu}$
, we first use the minimum typing property (Theorem 3.10) to obtain its minimum type B such that
$F_{\le}^{\mu}$
, we first use the minimum typing property (Theorem 3.10) to obtain its minimum type B such that
![]() $\Gamma \vdash_a e:B$
and
$\Gamma \vdash_a e:B$
and
![]() $\Gamma \vdash B \le A$
. Applying Lemmas 4.12 and 4.10, we complete the conservativity proof for the declarative version of
$\Gamma \vdash B \le A$
. Applying Lemmas 4.12 and 4.10, we complete the conservativity proof for the declarative version of
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Theorem 4.13 (Conservativity). If
![]() $\Gamma$
, A, and e are well formed in
$\Gamma$
, A, and e are well formed in
![]() $F_{\le}$
, namely (1)
$F_{\le}$
, namely (1)
![]() $\vdash_F \Gamma$
, (2)
$\vdash_F \Gamma$
, (2)
![]() $\Gamma \vdash_F A$
, and (3)
$\Gamma \vdash_F A$
, and (3)
![]() $\vdash_F e$
, then
$\vdash_F e$
, then
![]() $\Gamma \vdash_F e : A$
if and only if
$\Gamma \vdash_F e : A$
if and only if
![]() $\Gamma \vdash e:A$
.
$\Gamma \vdash e:A$
.
4.3 Decidability
This section focuses on the decidability of
![]() $\textrm{kernel}~F_{\le}^{\mu}$
. We first start by reviewing the approaches to proving decidability in
$\textrm{kernel}~F_{\le}^{\mu}$
. We first start by reviewing the approaches to proving decidability in
![]() $\textrm{kernel}~F_{\le}$
, and in nominal unfoldings, and then describe our approach to prove decidability. These two previous approaches to proving decidability employ different measures, which creates a challenge for proving the decidability of kernel
$\textrm{kernel}~F_{\le}$
, and in nominal unfoldings, and then describe our approach to prove decidability. These two previous approaches to proving decidability employ different measures, which creates a challenge for proving the decidability of kernel
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Decidability of
 $\textrm{kernel}~F_{\le}$
$\textrm{kernel}~F_{\le}$
It is well known that bounded quantification for
![]() $\textrm{full}~F_{\le}$
is undecidable (Pierce, Reference Pierce1994). However, for
$\textrm{full}~F_{\le}$
is undecidable (Pierce, Reference Pierce1994). However, for
![]() $\textrm{kernel}~F_{\le}$
, identical bounds make the system decidable. A common practice is to define a weight function to compute the size of a type (Pierce, Reference Pierce2002):
$\textrm{kernel}~F_{\le}$
, identical bounds make the system decidable. A common practice is to define a weight function to compute the size of a type (Pierce, Reference Pierce2002):

For a universal type, we store its bound into a context
![]() $\Gamma$
, and when we meet the universal variable, we retrieve its bound from the context and compute the size recursively. Since the size of a conclusion is always greater than any premise, this measure can be used to show that the subtyping algorithm in
$\Gamma$
, and when we meet the universal variable, we retrieve its bound from the context and compute the size recursively. Since the size of a conclusion is always greater than any premise, this measure can be used to show that the subtyping algorithm in
![]() $\textrm{kernel}~F_{\le}$
terminates for all inputs.
$\textrm{kernel}~F_{\le}$
terminates for all inputs.
Decidability of Nominal Unfoldings
The nominal unfolding rule in simple calculi with subtyping is also decidable (Zhou et al., Reference Zhou, Oliveira and Fan2022). Compared with
![]() $\textrm{kernel}~F_{\le}$
, the decidability proof of nominal unfoldings is trickier. Based on the substitution of the type body, after every unfolding, the size of types will increase. Thus, a straightforward induction on the size of types does not work. Zhou et al. (Reference Zhou, Oliveira and Fan2022) choose a size measure based on an over-approximation of the height of the fully unfolded tree. Concretely, the height of a type A in a measure context
$\textrm{kernel}~F_{\le}$
, the decidability proof of nominal unfoldings is trickier. Based on the substitution of the type body, after every unfolding, the size of types will increase. Thus, a straightforward induction on the size of types does not work. Zhou et al. (Reference Zhou, Oliveira and Fan2022) choose a size measure based on an over-approximation of the height of the fully unfolded tree. Concretely, the height of a type A in a measure context
![]() $\Psi$
(
$\Psi$
(
![]() $\Psi := \cdot ~|~ \Psi,\alpha \mapsto i$
, where i is a natural number) is defined as:
$\Psi := \cdot ~|~ \Psi,\alpha \mapsto i$
, where i is a natural number) is defined as:

The size measure of a type A is defined as
![]() $\textit{height}(A)$
where the context is empty. In contrast to
$\textit{height}(A)$
where the context is empty. In contrast to
![]() $\textrm{kernel}~F_{\le}$
, the context here is used to store the size of the corresponding recursive variables. The key design in the height function is that the measure of a recursive type
$\textrm{kernel}~F_{\le}$
, the context here is used to store the size of the corresponding recursive variables. The key design in the height function is that the measure of a recursive type
![]() ${\mu{\alpha}}.{A}$
is computed by first setting the measure of the recursive variable to 0 and then computing the measure of the body, which achieves the effect of measuring the type body A considering
${\mu{\alpha}}.{A}$
is computed by first setting the measure of the recursive variable to 0 and then computing the measure of the body, which achieves the effect of measuring the type body A considering
![]() $\alpha$
as a free variable. The computed measure is then incremented by one to account for the labeled type
$\alpha$
as a free variable. The computed measure is then incremented by one to account for the labeled type ![]() , then
, then
![]() $\textit{height}(A)$
is computed again with the context updated for the recursive variable, so that intuitively the result of
$\textit{height}(A)$
is computed again with the context updated for the recursive variable, so that intuitively the result of
![]() $\textit{height}({\mu{\alpha}}.{A})$
measures the size of
$\textit{height}({\mu{\alpha}}.{A})$
measures the size of ![]() plus one. Zhou et al. (Reference Zhou, Oliveira and Fan2022) prove that such height measure works well with nominal unfolding rules, as the height of a type will precisely decrease by one for every nominal unfolding.
plus one. Zhou et al. (Reference Zhou, Oliveira and Fan2022) prove that such height measure works well with nominal unfolding rules, as the height of a type will precisely decrease by one for every nominal unfolding.
Decidability of Kernel
 $F_{\le}^{\mu}$
$F_{\le}^{\mu}$
To combine these two approaches, we need to extend the measure of nominal unfoldings with the measure of
![]() $\textrm{kernel}~F_{\le}$
in a seamless manner. One easy fix to unify the two measures is to use the maximum function for both measures, as the nominal unfolding measure does. However, there are three remaining main challenges that we must address:
$\textrm{kernel}~F_{\le}$
in a seamless manner. One easy fix to unify the two measures is to use the maximum function for both measures, as the nominal unfolding measure does. However, there are three remaining main challenges that we must address:
-
• Inconsistent measures for variables: In the height function, type variables are treated as base cases, whereas in the weight function, the computation continues by retrieving the variable’s bound from the context. In kernel
 $F_{\le}^{\mu}$
, we do not distinguish between recursive and universal variables, so we need to find a unified way to measure variables.
$F_{\le}^{\mu}$
, we do not distinguish between recursive and universal variables, so we need to find a unified way to measure variables. -
• Different purposes of contexts: The context in the weight function straightforwardly keeps track of universal bounds, which are later retrieved to compute the measure of a universal variable. This ensures that the premises in rule S-vartrans have smaller type measures than the conclusion. However, this trick does not work for nominal unfoldings, as shown by the case
 $\textit{height}_{\Psi}({\mu{\alpha}}.{A})$
, where the context is extended with two different measures for the same variable at different points in the computation to simulate the nominal unfolding. This discrepancy complicates the unification of the two measures.
$\textit{height}_{\Psi}({\mu{\alpha}}.{A})$
, where the context is extended with two different measures for the same variable at different points in the computation to simulate the nominal unfolding. This discrepancy complicates the unification of the two measures. -
• Loss of measure information with equivalent bounds: We use rule S-equivall instead of the standard rule S-kernelall for
 $F_{\le}$
. Given the equivalent bounds in
$F_{\le}$
. Given the equivalent bounds in
 $\textrm{kernel}~F_{\le}$
, the measure for the subtyping relation
$\textrm{kernel}~F_{\le}$
, the measure for the subtyping relation
 $\Gamma \vdash \forall({\alpha}\le{A_1}).{B_1} \le \forall({\alpha}\le{A_2}).{B_2}$
includes the measures of
$\Gamma \vdash \forall({\alpha}\le{A_1}).{B_1} \le \forall({\alpha}\le{A_2}).{B_2}$
includes the measures of
 $A_1$
,
$A_1$
,
 $A_2$
,
$A_2$
,
 $B_1$
, and
$B_1$
, and
 $B_2$
. However, the measure for the premise
$B_2$
. However, the measure for the premise
 $\Gamma,\alpha\le A_2 \vdash B_1 \le B_2$
loses the measure of
$\Gamma,\alpha\le A_2 \vdash B_1 \le B_2$
loses the measure of
 $A_1$
because it is not stored.
$A_1$
because it is not stored.
We first show the measure used for the decidability of kernel
![]() $F_{\le}^{\mu}$
and then discuss how it addresses the concerns above. The measure is relatively simple and based on the approach from Zhou et al. (Reference Zhou, Oliveira and Fan2022). We use the same context
$F_{\le}^{\mu}$
and then discuss how it addresses the concerns above. The measure is relatively simple and based on the approach from Zhou et al. (Reference Zhou, Oliveira and Fan2022). We use the same context
![]() $\Psi :=\cdot \mid \Psi, \alpha \mapsto i$
and now it is used to store the measures of (both universal and recursive) variables during the measure computation. Then, a measure function
$\Psi :=\cdot \mid \Psi, \alpha \mapsto i$
and now it is used to store the measures of (both universal and recursive) variables during the measure computation. Then, a measure function
![]() $\textit{size}_{\Psi}(A)$
, is defined on types as follows:
$\textit{size}_{\Psi}(A)$
, is defined on types as follows:

The formulation of the size function is very similar to the height function. We have an extra rule for universal types and slightly adjust the variable and recursive cases. The measure of universal types is the sum of the measure of the bound and the measure of the body. For variables, one is added when they are retrieved. Accordingly, we do not need to add one when storing the size of recursive variables into the context. For atomic constructs, we follow the weight function and measure them as 1.
We solve the first challenge in a straightforward way: there is no need to distinguish between recursive and universal variables. The fact that all recursive variables in the context are bounded by a top type whose measure is simply the one that fits our needs naturally.
As for the second concern, despite the different purposes of contexts, the key ideas of measuring types in
![]() $\textrm{kernel}~F_{\le}$
and nominal unfoldings are the same: they both relate the measure of a variable to what the variable will be substituted with in the context of the subtyping rule, either its unfolded form as a labeled type or its bound type. A slight modification is made based on the definition of weight. In the weight function, for a universal variable, its bound is first retrieved and then the measure is computed. To align with the “pre-computation” mechanism of measuring nominal unfoldings (
$\textrm{kernel}~F_{\le}$
and nominal unfoldings are the same: they both relate the measure of a variable to what the variable will be substituted with in the context of the subtyping rule, either its unfolded form as a labeled type or its bound type. A slight modification is made based on the definition of weight. In the weight function, for a universal variable, its bound is first retrieved and then the measure is computed. To align with the “pre-computation” mechanism of measuring nominal unfoldings (
![]() $i := \textit{size}_{\Psi, \alpha \mapsto 1}(A)$
), we also pre-compute the measure of the bound (
$i := \textit{size}_{\Psi, \alpha \mapsto 1}(A)$
), we also pre-compute the measure of the bound (
![]() $i := \textit{size}_{\Psi}(A)$
) in the size function so that we retrieve the measure instead of the type bound from the context. In a well-formed type, variables are guaranteed to be unique, so we can use a single context
$i := \textit{size}_{\Psi}(A)$
) in the size function so that we retrieve the measure instead of the type bound from the context. In a well-formed type, variables are guaranteed to be unique, so we can use a single context
![]() $\Psi$
to store the measures for both recursive variables and universal variables.
$\Psi$
to store the measures for both recursive variables and universal variables.
A subtler issue arises with variables in the initial subtyping context. When measuring nominal unfoldings, the context in a subtyping relation is simply a list of variables, without any bound information, so variables that occur freely can be counted as 0 in the height function. In contrast, now the subtyping context stores the bound information, and the measures of bounds play a role in deciding the subtyping relation. To address this issue, we need to make sure that the bound information is pre-computed in the measure function. We transform a subtyping context into an environment containing measures
![]() $\Psi$
, which track universal variables. In our decidability proof statement (Lemma 4.14),
$\Psi$
, which track universal variables. In our decidability proof statement (Lemma 4.14),
![]() $\Psi$
is computed from the subtyping context
$\Psi$
is computed from the subtyping context
![]() $\Gamma$
by an evaluation function
$\Gamma$
by an evaluation function
![]() $eval : \Gamma \hookrightarrow \Psi$
, defined as:
$eval : \Gamma \hookrightarrow \Psi$
, defined as:
 $$\begin{array}{l c l} \textit{eval}(\cdot) &=& \cdot \\ \textit{eval}(\Gamma',~x : A) &=& \textit{eval}(\Gamma') \\ \textit{eval}(\Gamma',~\alpha \le A) &=& \textrm{let } \Psi' = \textit{eval}(\Gamma') \textrm{ in } \Psi', \alpha \mapsto \textit{size}_{\Psi'}(A) \\\end{array}$$
$$\begin{array}{l c l} \textit{eval}(\cdot) &=& \cdot \\ \textit{eval}(\Gamma',~x : A) &=& \textit{eval}(\Gamma') \\ \textit{eval}(\Gamma',~\alpha \le A) &=& \textrm{let } \Psi' = \textit{eval}(\Gamma') \textrm{ in } \Psi', \alpha \mapsto \textit{size}_{\Psi'}(A) \\\end{array}$$
With both eval and size, we can then state the decidability theorem:
Lemma 4.14. If
![]() $\textit{size}_{\textit{eval}(\Gamma)}(A) + \textit{size}_{\textit{eval}(\Gamma)}(B) \le k$
, then there exists an algorithm that terminates and decides whether
$\textit{size}_{\textit{eval}(\Gamma)}(A) + \textit{size}_{\textit{eval}(\Gamma)}(B) \le k$
, then there exists an algorithm that terminates and decides whether
![]() $\Gamma \vdash A \le B$
.
$\Gamma \vdash A \le B$
.
Theorem 4.15 (Decidability of
![]() $\textrm{kernel}~F_{\le}^{\mu}$
subtyping).
$\textrm{kernel}~F_{\le}^{\mu}$
subtyping).
![]() $\Gamma \vdash A \le B$
is decidable in
$\Gamma \vdash A \le B$
is decidable in
![]() $\textrm{kernel}~F_{\le}^{\mu}$
.
$\textrm{kernel}~F_{\le}^{\mu}$
.
Theorem 4.16 (Decidability of
![]() $\textrm{kernel}~F_{\le}^{\mu}$
typing).
$\textrm{kernel}~F_{\le}^{\mu}$
typing).
![]() $\Gamma \vdash e : A$
is decidable in
$\Gamma \vdash e : A$
is decidable in
![]() $\textrm{kernel}~F_{\le}^{\mu}$
.
$\textrm{kernel}~F_{\le}^{\mu}$
.
As for the third concern, note that in
![]() $F_{\le}$
, the subtyping relation is antisymmetric (Baldan et al., Reference Baldan, Ghelli and Raffaetà1999). Adding recursive types does not change the property of antisymmetry. However, the addition of records makes the subtyping relation not antisymmetric: two equivalent record types may be syntactically different. The lack of antisymmetry poses a challenge to our decidability proof, particularly for rule S-equivall. Nevertheless, for
$F_{\le}$
, the subtyping relation is antisymmetric (Baldan et al., Reference Baldan, Ghelli and Raffaetà1999). Adding recursive types does not change the property of antisymmetry. However, the addition of records makes the subtyping relation not antisymmetric: two equivalent record types may be syntactically different. The lack of antisymmetry poses a challenge to our decidability proof, particularly for rule S-equivall. Nevertheless, for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
two equivalent records must have the same set of fields, and the two types for each field must be equivalent. Therefore, the measures of two equivalent record types remain the same. As a result, the measure of two equivalent bounds
$\textrm{kernel}~F_{\le}^{\mu}$
two equivalent records must have the same set of fields, and the two types for each field must be equivalent. Therefore, the measures of two equivalent record types remain the same. As a result, the measure of two equivalent bounds
![]() $A_1$
and
$A_1$
and
![]() $A_2$
is equal, as Lemma 4.17 describes. The measure information of type
$A_2$
is equal, as Lemma 4.17 describes. The measure information of type
![]() $A_1$
can therefore be reconstructed from type
$A_1$
can therefore be reconstructed from type
![]() $A_2$
, addressing the final concern with decidability.
$A_2$
, addressing the final concern with decidability.
Lemma 4.17 If
![]() $\Gamma \vdash A \le B$
and
$\Gamma \vdash A \le B$
and
![]() $\Gamma \vdash B \le A$
, then
$\Gamma \vdash B \le A$
, then
![]() $\textit{size}_{\textit{eval}(\Gamma)}(A) = \textit{size}_{\textit{eval}(\Gamma)}(B)$
.
$\textit{size}_{\textit{eval}(\Gamma)}(A) = \textit{size}_{\textit{eval}(\Gamma)}(B)$
.
Undecidability of Subtyping
 $\textrm{full}~F_{\le}^{\mu}$
$\textrm{full}~F_{\le}^{\mu}$
It is well known that the
![]() $\textrm{full}~F_{\le}$
subtyping relation is undecidable (Pierce, Reference Pierce1994). Although the original formulation of
$\textrm{full}~F_{\le}$
subtyping relation is undecidable (Pierce, Reference Pierce1994). Although the original formulation of
![]() $\textrm{full}~F_{\le}$
includes the transitivity rule, it can be reformulated into a syntax-directed version (Curien & Ghelli, Reference Curien and Ghelli1992) that eliminates the transitivity rule, as we have adopted in
$\textrm{full}~F_{\le}$
includes the transitivity rule, it can be reformulated into a syntax-directed version (Curien & Ghelli, Reference Curien and Ghelli1992) that eliminates the transitivity rule, as we have adopted in
![]() $F_{\le}^{\mu}$
. The syntax-directed version of
$F_{\le}^{\mu}$
. The syntax-directed version of
![]() $F_{\le}$
naturally forms a subtype checking algorithm. However, for
$F_{\le}$
naturally forms a subtype checking algorithm. However, for
![]() $\textrm{full}~F_{\le}$
, Ghelli (Reference Ghelli1993) demonstrated a non-terminating example for the subtyping algorithm. Furthermore, Pierce (Reference Pierce1994) proved the undecidability of
$\textrm{full}~F_{\le}$
, Ghelli (Reference Ghelli1993) demonstrated a non-terminating example for the subtyping algorithm. Furthermore, Pierce (Reference Pierce1994) proved the undecidability of
![]() $\textrm{full}~F_{\le}$
by encoding a Turing machine using
$\textrm{full}~F_{\le}$
by encoding a Turing machine using
![]() $\textrm{full}~F_{\le}$
. Since we have shown in Section 4.2 that
$\textrm{full}~F_{\le}$
. Since we have shown in Section 4.2 that
![]() $\textrm{full}~F_{\le}^{\mu}$
is conservative over the syntax-directed version of
$\textrm{full}~F_{\le}^{\mu}$
is conservative over the syntax-directed version of
![]() $\textrm{full}~F_{\le}$
, Ghelli (Reference Ghelli1993)’s counterexample for
$\textrm{full}~F_{\le}$
, Ghelli (Reference Ghelli1993)’s counterexample for
![]() $\textrm{full}~F_{\le}$
also applies to
$\textrm{full}~F_{\le}$
also applies to
![]() $\textrm{full}~F_{\le}^{\mu}$
. Therefore, the undecidability of
$\textrm{full}~F_{\le}^{\mu}$
. Therefore, the undecidability of
![]() $\textrm{full}~F_{\le}^{\mu}$
is a corollary of the undecidability of
$\textrm{full}~F_{\le}^{\mu}$
is a corollary of the undecidability of
![]() $\textrm{full}~F_{\le}$
and the conservativity of
$\textrm{full}~F_{\le}$
and the conservativity of
![]() $\textrm{full}~F_{\le}^{\mu}$
over
$\textrm{full}~F_{\le}^{\mu}$
over
![]() $\textrm{full}~F_{\le}$
.
$\textrm{full}~F_{\le}$
.
Theorem 4.18 (Undecidability of typing and subtyping for
![]() $\textrm{full}~F_{\le}^{\mu}$
). The subtyping relation
$\textrm{full}~F_{\le}^{\mu}$
). The subtyping relation
![]() $\Gamma \vdash A \le B$
and the typing relation
$\Gamma \vdash A \le B$
and the typing relation
![]() $\Gamma \vdash e : A$
are undecidable in
$\Gamma \vdash e : A$
are undecidable in
![]() $\textrm{full}~F_{\le}^{\mu}$
.
$\textrm{full}~F_{\le}^{\mu}$
.
5 A calculus with lower and upper bounded quantification
In this section, we introduce an extension of
![]() $F_{\le}^{\mu}$
, called
$F_{\le}^{\mu}$
, called
![]() $F_{\le\ge}^{\mu\wedge}$
, with lower bounded quantification, the bottom type, and an alternative formulation of record types in terms of intersections of single field record types. While upper bounded quantification has received a lot of attention in previous research, lower bounded quantification for an
$F_{\le\ge}^{\mu\wedge}$
, with lower bounded quantification, the bottom type, and an alternative formulation of record types in terms of intersections of single field record types. While upper bounded quantification has received a lot of attention in previous research, lower bounded quantification for an
![]() $F_{\le}$
-like language is much less explored, though it appears in a few works (Amin & Rompf, Reference Amin and Rompf2017; Oliveira et al., 2020). We follow the same approach as Oliveira et al. (2020), whose
$F_{\le}$
-like language is much less explored, though it appears in a few works (Amin & Rompf, Reference Amin and Rompf2017; Oliveira et al., 2020). We follow the same approach as Oliveira et al. (2020), whose
![]() $F_{\le}$
extension allows type variables to have either a lower bound or an upper bound, but not both bounds at once. We also introduce single-field record types and intersection types to replace record types in
$F_{\le}$
extension allows type variables to have either a lower bound or an upper bound, but not both bounds at once. We also introduce single-field record types and intersection types to replace record types in
![]() $F_{\le}^{\mu}$
. Intersection types enable type-level record extension and further applications resembling the treatment of object types in the DOT calculus (Rompf & Amin, Reference Rompf and Amin2016). As discussed in Section 2.2, our extensions in
$F_{\le}^{\mu}$
. Intersection types enable type-level record extension and further applications resembling the treatment of object types in the DOT calculus (Rompf & Amin, Reference Rompf and Amin2016). As discussed in Section 2.2, our extensions in
![]() $F_{\le\ge}^{\mu\wedge}$
enable further applications, such as a form of extensible encodings of datatypes. We have proved all the same results for
$F_{\le\ge}^{\mu\wedge}$
enable further applications, such as a form of extensible encodings of datatypes. We have proved all the same results for
![]() $F_{\le\ge}^{\mu\wedge}$
that were proved for
$F_{\le\ge}^{\mu\wedge}$
that were proved for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
, including type soundness, decidability, transitivity, and conservativity over
$\textrm{kernel}~F_{\le}^{\mu}$
, including type soundness, decidability, transitivity, and conservativity over
![]() $F_\le$
.
$F_\le$
.
5.1 The
 $F_{\le\ge}^{\mu\wedge}$
calculus
$F_{\le\ge}^{\mu\wedge}$
calculus
The syntax of types, expressions, values, and contexts for the extended
![]() $F_{\le\ge}^{\mu\wedge}$
calculus is shown below. The main novelties are that bottom types and lower bounded quantification are introduced. We also remove record types (
$F_{\le\ge}^{\mu\wedge}$
calculus is shown below. The main novelties are that bottom types and lower bounded quantification are introduced. We also remove record types (
![]() $\{ l_i : A_i ~ ^{i \in 1\cdots n}\}$
) from the syntax and instead introduce intersection types and single-field record types. The syntactic differences are highlighted in
$\{ l_i : A_i ~ ^{i \in 1\cdots n}\}$
) from the syntax and instead introduce intersection types and single-field record types. The syntactic differences are highlighted in ![]() .
.

Subtyping, Typing and Reduction
The well-formedness for the additional bottom types, single-field record types, and universal types with lower bounds are standard, as shown in Figure 6. For intersection types, we only allow single-field record types, or intersections of record types with distinct labels to be well formed. This can be characterized by a compatibility relation
![]() $A\,\#\,B$
between types. We make this simplified design choice to avoid the complexity of general unrestricted intersection types, which would cause trouble in the two key properties of the type system, namely the structural unfolding lemma (Lemma 5.11) and the decidability of subtyping (Theorem 5.14), as we will discuss in Section 5.3.
$A\,\#\,B$
between types. We make this simplified design choice to avoid the complexity of general unrestricted intersection types, which would cause trouble in the two key properties of the type system, namely the structural unfolding lemma (Lemma 5.11) and the decidability of subtyping (Theorem 5.14), as we will discuss in Section 5.3.

Fig. 6. Additional well-formedness and subtyping rules for
![]() $F_{\le\ge}^{\mu\wedge}$
with respect to
$F_{\le\ge}^{\mu\wedge}$
with respect to
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
As for the subtyping rules, compared with
![]() $F_{\le}^{\mu}$
, we add rules S-bot,S-vartranslb,S-equivalllb for subtyping with bottom types and lower bounded quantification. The record subtyping rule S-rcd in
$F_{\le}^{\mu}$
, we add rules S-bot,S-vartranslb,S-equivalllb for subtyping with bottom types and lower bounded quantification. The record subtyping rule S-rcd in
![]() $F_{\le}^{\mu}$
is now replaced by rule S-srcd for subtyping single-field record types together with S-andla,S-andlb,S-andr for subtyping intersection types. Note that in the subtyping rule for intersection types, we also add the compatibility restriction in the premise, to ensure the regularity of the subtyping relation (Lemma 5.1).
$F_{\le}^{\mu}$
is now replaced by rule S-srcd for subtyping single-field record types together with S-andla,S-andlb,S-andr for subtyping intersection types. Note that in the subtyping rule for intersection types, we also add the compatibility restriction in the premise, to ensure the regularity of the subtyping relation (Lemma 5.1).
Lemma 5.1 (Regularity of subtyping in
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash A \le B$
, then the following well-formedness conditions hold: (1)
$\Gamma \vdash A \le B$
, then the following well-formedness conditions hold: (1)
![]() $\vdash \Gamma$
, (2)
$\vdash \Gamma$
, (2)
![]() $\Gamma \vdash A$
, and (3)
$\Gamma \vdash A$
, and (3)
![]() $\Gamma \vdash B$
.
$\Gamma \vdash B$
.
The new subtyping relation is reflexive and transitive:
Theorem 5.2 (Reflexivity for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\vdash \Gamma$
and
$\vdash \Gamma$
and
![]() $\Gamma \vdash A$
, then
$\Gamma \vdash A$
, then
![]() $\Gamma \vdash A \le A$
.
$\Gamma \vdash A \le A$
.
Theorem 5.3 (Transitivity for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash A \le B$
and
$\Gamma \vdash A \le B$
and
![]() $\Gamma \vdash B \le C$
, then
$\Gamma \vdash B \le C$
, then
![]() $\Gamma \vdash A \le C$
.
$\Gamma \vdash A \le C$
.
Figure 7 shows the changes of
![]() $F_{\le\ge}^{\mu\wedge}$
with respect to
$F_{\le\ge}^{\mu\wedge}$
with respect to
![]() $F_{\le}^{\mu}$
in terms of typing and reduction. For lower bounded quantification, we add rules typing-tapplb,typing-tabslb for typing and rule step-tabslb for reduction, which are simply dual forms of rules typing-tapp,typing-tabs, and step-tabs, respectively. For records, since the syntax of record expressions is unchanged, there are no further changes in the reduction rules. The typing rule for record projections is also simplified. Since record types are now represented by single-field record types, the projection of a record can be directly modeled by the subtyping relation. typing-rcdnil,typing-srcd form the typing rules for record expressions.
$F_{\le}^{\mu}$
in terms of typing and reduction. For lower bounded quantification, we add rules typing-tapplb,typing-tabslb for typing and rule step-tabslb for reduction, which are simply dual forms of rules typing-tapp,typing-tabs, and step-tabs, respectively. For records, since the syntax of record expressions is unchanged, there are no further changes in the reduction rules. The typing rule for record projections is also simplified. Since record types are now represented by single-field record types, the projection of a record can be directly modeled by the subtyping relation. typing-rcdnil,typing-srcd form the typing rules for record expressions.

Fig. 7. Additional typing and reduction rules for
![]() $F_{\le\ge}^{\mu\wedge}$
with respect to
$F_{\le\ge}^{\mu\wedge}$
with respect to
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Structural Folding and Lower Bounded Quantification
The structural folding rule typing-sfold on recursive types has already been shown for
![]() $F_{\le}^{\mu}$
. Note that this rule is not strictly necessary for
$F_{\le}^{\mu}$
. Note that this rule is not strictly necessary for
![]() $F_{\le}^{\mu}$
, because a recursive type can only be a subtype of another recursive type or the
$F_{\le}^{\mu}$
, because a recursive type can only be a subtype of another recursive type or the
![]() $\top$
type. Thus, the effect of structural folding in
$\top$
type. Thus, the effect of structural folding in
![]() $F_{\le}^{\mu}$
can be subsumed by other subtyping/typing rules. Perhaps for this reason, Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996) have only considered a structural unfolding rule. However, in
$F_{\le}^{\mu}$
can be subsumed by other subtyping/typing rules. Perhaps for this reason, Abadi et al. (Reference Abadi, Cardelli and Viswanathan1996) have only considered a structural unfolding rule. However, in
![]() $F_{\le\ge}^{\mu\wedge}$
, a recursive type can also be a subtype of a type variable. In this case, the structural folding rule can give the desired typings to the
$F_{\le\ge}^{\mu\wedge}$
, a recursive type can also be a subtype of a type variable. In this case, the structural folding rule can give the desired typings to the
![]() $\textsf{Add}_{\forall}$
constructors of the
$\textsf{Add}_{\forall}$
constructors of the
![]() $\textsf{Exp}_1$
and
$\textsf{Exp}_1$
and
![]() $\textsf{Exp}_2$
datatypes that we have presented in Section 2.2, while the standard folding rule cannot. The rule typing-sfold has the same form in
$\textsf{Exp}_2$
datatypes that we have presented in Section 2.2, while the standard folding rule cannot. The rule typing-sfold has the same form in
![]() $F_{\le\ge}^{\mu\wedge}$
as in
$F_{\le\ge}^{\mu\wedge}$
as in
![]() $F_{\le}^{\mu}$
. Therefore, we believe that the structural folding rule that we have proposed, together with the structural unfolding lemma in the metatheory, is broadly applicable to various type system extensions to
$F_{\le}^{\mu}$
. Therefore, we believe that the structural folding rule that we have proposed, together with the structural unfolding lemma in the metatheory, is broadly applicable to various type system extensions to
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Type Soundness
Our type soundness proof for
![]() $F_{\le\ge}^{\mu\wedge}$
is standard:
$F_{\le\ge}^{\mu\wedge}$
is standard:
Theorem 5.4 (Preservation for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $ \vdash e : A $
and
$ \vdash e : A $
and
![]() $e \hookrightarrow e'$
then
$e \hookrightarrow e'$
then
![]() $ \vdash e' : A$
.
$ \vdash e' : A$
.
Theorem 5.5 (Progress for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\vdash e : A $
then e is a value or exists
$\vdash e : A $
then e is a value or exists
![]() $e', e \hookrightarrow e'$
.
$e', e \hookrightarrow e'$
.
5.2 Algorithmic typing
Similarly to
![]() $F_{\le}^{\mu}$
, we can define an algorithmic typing system for
$F_{\le}^{\mu}$
, we can define an algorithmic typing system for
![]() $F_{\le\ge}^{\mu\wedge}$
. We present the changes in the algorithmic typing rules for
$F_{\le\ge}^{\mu\wedge}$
. We present the changes in the algorithmic typing rules for
![]() $F_{\le\ge}^{\mu\wedge}$
in Figure 8. Rules atyp-tabslb and atyp-tapplb are added to handle lower bounded quantification. Rules atyp-rcdnil and atyp-srcd replace the record typing rule typing-rcd in
$F_{\le\ge}^{\mu\wedge}$
in Figure 8. Rules atyp-tabslb and atyp-tapplb are added to handle lower bounded quantification. Rules atyp-rcdnil and atyp-srcd replace the record typing rule typing-rcd in
![]() $F_{\le}^{\mu}$
. In addition to these standard changes, there are also a few special cases that need to be handled for
$F_{\le}^{\mu}$
. In addition to these standard changes, there are also a few special cases that need to be handled for
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.

Fig. 8. The additional algorithmic typing rules for
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
First, bottom types bring several extra cases to the algorithmic typing rules. In the declarative system, one can always use the subsumption rule to transform a term with type
![]() $\bot$
to any function type or universal type and apply it to any argument, as also observed by Pierce (Reference Pierce1997). To ensure that the algorithmic typing rules are complete, we need to add rules atyp-appbot and atyp-tappbot to handle these cases. We also develop a similar treatment for recursive types, as shown in rules atyp-sunfoldbot and atyp-sfoldtop.
$\bot$
to any function type or universal type and apply it to any argument, as also observed by Pierce (Reference Pierce1997). To ensure that the algorithmic typing rules are complete, we need to add rules atyp-appbot and atyp-tappbot to handle these cases. We also develop a similar treatment for recursive types, as shown in rules atyp-sunfoldbot and atyp-sfoldtop.
Moreover, with two kinds of bounded quantification, the meanings of the two exposure functions also need to be refined. For example, the upper exposure function (
![]() $\Uparrow$
) is now used to find the least upper bound in the context that is not an upper-bounded variable, so it will return the variable itself if the variable is lower bounded. We redefine the exposure functions for
$\Uparrow$
) is now used to find the least upper bound in the context that is not an upper-bounded variable, so it will return the variable itself if the variable is lower bounded. We redefine the exposure functions for
![]() $F_{\le\ge}^{\mu\wedge}$
in Figure 9. For lower exposure, we also need a dual form of the rule XA-promote, which finds the greatest lower bound in the context that is not a lower-bounded variable, as shown in rule XA-downpromote.
$F_{\le\ge}^{\mu\wedge}$
in Figure 9. For lower exposure, we also need a dual form of the rule XA-promote, which finds the greatest lower bound in the context that is not a lower-bounded variable, as shown in rule XA-downpromote.

Fig. 9. The new exposure functions for
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Record Exposure
Furthermore, for typing record projections, recall that in the declarative rule typing-sproj, the lookup of the field label l is implied by the implicit subtyping between the expression type and the single-field record type for
![]() $\{l:A\}$
. In the algorithmic system, we need to find a mechanism to find such A. Therefore, we define a new exposure relation for record types in
$\{l:A\}$
. In the algorithmic system, we need to find a mechanism to find such A. Therefore, we define a new exposure relation for record types in
![]() $F_{\le\ge}^{\mu\wedge}$
. The record exposure relation
$F_{\le\ge}^{\mu\wedge}$
. The record exposure relation
![]() $\Gamma \vdash A \Rightarrow_l B$
indicates that from the type A we can lookup the field label l and get the type B. We show the full definition of the record exposure relation in Figure 9. Note that, in addition to single-field record types (rule XR-srcd) and intersection types (Rules XR-anda,XR-andb,XR-andr), one can also lookup
$\Gamma \vdash A \Rightarrow_l B$
indicates that from the type A we can lookup the field label l and get the type B. We show the full definition of the record exposure relation in Figure 9. Note that, in addition to single-field record types (rule XR-srcd) and intersection types (Rules XR-anda,XR-andb,XR-andr), one can also lookup
![]() $\bot$
from
$\bot$
from
![]() $\bot$
(XR-bot), as well as upper bounds from upper bounded variables (XR-promote). With the record exposure relation, we define atyp-sproj for record projections to replace atyp-proj in
$\bot$
(XR-bot), as well as upper bounds from upper bounded variables (XR-promote). With the record exposure relation, we define atyp-sproj for record projections to replace atyp-proj in
![]() $F_{\le}^{\mu}$
. The record exposure relation is sound and complete for the subtyping relation
$F_{\le}^{\mu}$
. The record exposure relation is sound and complete for the subtyping relation
![]() $A \le \{l:B\}$
.
$A \le \{l:B\}$
.
Lemma 5.6 (Record exposure properties for
![]() $F_{\le\ge}^{\mu\wedge}$
).
$F_{\le\ge}^{\mu\wedge}$
).
-
1. If
 $\Gamma \vdash A \Rightarrow_l B$
then
$\Gamma \vdash A \Rightarrow_l B$
then
 $\Gamma \vdash A \le \{l:B\}$
.
$\Gamma \vdash A \le \{l:B\}$
. -
2. If
 $\Gamma \vdash A \le \{l:B\}$
then there exists C such that
$\Gamma \vdash A \le \{l:B\}$
then there exists C such that
 $\Gamma \vdash A \Rightarrow_l C$
and
$\Gamma \vdash A \Rightarrow_l C$
and
 $\Gamma \vdash C \le \{l:B\}$
.
$\Gamma \vdash C \le \{l:B\}$
.
With these considerations in the algorithmic typing rules, we prove the soundness and completeness of the algorithmic typing system with respect to the declarative typing rules defined in Figure 7.
Theorem 5.7 (Soundness of the algorithmic rules for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash_a e : A $
then
$\Gamma \vdash_a e : A $
then
![]() $\Gamma \vdash e : A $
.
$\Gamma \vdash e : A $
.
Theorem 5.8 (Completeness of the algorithmic rules for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash e : A $
then there exists B such that
$\Gamma \vdash e : A $
then there exists B such that
![]() $\Gamma \vdash_a e : B $
and
$\Gamma \vdash_a e : B $
and
![]() $\Gamma \vdash B \le A$
.
$\Gamma \vdash B \le A$
.
5.3 Metatheory of
 $F_{\le\ge}^{\mu\wedge}$
$F_{\le\ge}^{\mu\wedge}$
The addition of lower bounded quantification, bottom types, and intersection types creates some difficulties in the metatheory of
![]() $F_{\le\ge}^{\mu\wedge}$
. In the following, we describe how to overcome the difficulties, by adjusting the proof techniques we have used for
$F_{\le\ge}^{\mu\wedge}$
. In the following, we describe how to overcome the difficulties, by adjusting the proof techniques we have used for
![]() $F_{\le}^{\mu}$
.
$F_{\le}^{\mu}$
.
Unfolding Lemma
As discussed in Section 4.1, in a type system that simultaneously allows introducing lower and upper bounded types, the inversion lemma for rule S-vartrans (Lemma 4.4) is not valid. This is exactly the case for
![]() $F_{\le\ge}^{\mu\wedge}$
. To resolve this issue, the unfolding lemmas should only state the subtyping relation between the nominal unfoldings
$F_{\le\ge}^{\mu\wedge}$
. To resolve this issue, the unfolding lemmas should only state the subtyping relation between the nominal unfoldings ![]() and remove the one-step unfolding relation
and remove the one-step unfolding relation
![]() $A \le B$
from the premise. Therefore, we use the same statement of the generalized unfolding lemma as in
$A \le B$
from the premise. Therefore, we use the same statement of the generalized unfolding lemma as in
![]() $\textrm{full}~F_{\le}^{\mu}$
(Lemma 4.9), under an extended version of related contexts (Definition 4.7) that takes lower bounded bindings into account. It turns out that, with only changes of the proof in cases S-equivall and S-equivalllb, the generalized unfolding lemma can be proved for
$\textrm{full}~F_{\le}^{\mu}$
(Lemma 4.9), under an extended version of related contexts (Definition 4.7) that takes lower bounded bindings into account. It turns out that, with only changes of the proof in cases S-equivall and S-equivalllb, the generalized unfolding lemma can be proved for
![]() $F_{\le\ge}^{\mu\wedge}$
as well, which results in the following unfolding lemma for
$F_{\le\ge}^{\mu\wedge}$
as well, which results in the following unfolding lemma for
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Lemma 5.9 (Unfolding lemma for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
, then
$\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{B}$
, then
![]() $\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{A}]~A \le [\alpha \mapsto {\mu{\alpha}}.{B}]~B$
.
$\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{A}]~A \le [\alpha \mapsto {\mu{\alpha}}.{B}]~B$
.
To prove type soundness, we need to show the structural unfolding lemma. If we check the typing derivation with structural folding and unfolding illustrated in Figure 4 again in
![]() $F_{\le\ge}^{\mu\wedge}$
, we can see that by inversion on the subtyping relation
$F_{\le\ge}^{\mu\wedge}$
, we can see that by inversion on the subtyping relation
![]() $\cdot \vdash {\mu{\alpha}}.{A} \le C'$
and
$\cdot \vdash {\mu{\alpha}}.{A} \le C'$
and
![]() $\cdot \vdash D' \le {\mu{\alpha}}.{B}$
, we can no longer guarantee that C’ and D’ are recursive types, since they can also be intersection types. To remedy this, the compatibility relation
$\cdot \vdash D' \le {\mu{\alpha}}.{B}$
, we can no longer guarantee that C’ and D’ are recursive types, since they can also be intersection types. To remedy this, the compatibility relation
![]() $A \,\#\,\, B$
is enforced by the well-formedness of intersection types so that intersection types can only be formed from single-field record types, not by recursive types. We can prove the following lemma to derive a contradiction for the case of intersection types and recover the structural unfolding lemma as well as type soundness for
$A \,\#\,\, B$
is enforced by the well-formedness of intersection types so that intersection types can only be formed from single-field record types, not by recursive types. We can prove the following lemma to derive a contradiction for the case of intersection types and recover the structural unfolding lemma as well as type soundness for
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Lemma 5.10. For any types A,
![]() $B_1$
, and
$B_1$
, and
![]() $B_2$
, it cannot happen that
$B_2$
, it cannot happen that
![]() ${\mu{\alpha}}.{A} \le B_1 \,\&\, B_2$
or
${\mu{\alpha}}.{A} \le B_1 \,\&\, B_2$
or
![]() $B_1 \,\&\, B_2 \le {\mu{\alpha}}.{A}$
in
$B_1 \,\&\, B_2 \le {\mu{\alpha}}.{A}$
in
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Lemma 5.11 (Structural unfolding lemma for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{B}$
, then
$\Gamma \vdash {\mu{\alpha}}.{A} \le {\mu{\alpha}}.{C} \le {\mu{\alpha}}.{D} \le {\mu{\alpha}}.{B}$
, then
![]() $\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}] ~B$
.
$\Gamma \vdash [\alpha \mapsto {\mu{\alpha}}.{C}]~A \le [\alpha \mapsto {\mu{\alpha}}.{D}] ~B$
.
Decidability
The interaction between bottom types and rule S-equivall breaks the measure-based decidability proof in Section 4.3. The bottom type in
![]() $F_{\le\ge}^{\mu\wedge}$
brings a new form of equivalent types: when
$F_{\le\ge}^{\mu\wedge}$
brings a new form of equivalent types: when
![]() $ \alpha \le \bot \in \Gamma$
, one can derive that
$ \alpha \le \bot \in \Gamma$
, one can derive that
![]() $\Gamma \vdash \alpha \le \bot$
and
$\Gamma \vdash \alpha \le \bot$
and
![]() $\Gamma \vdash \bot \le\alpha$
, as observed by Pierce (Reference Pierce1997). Simply extending the measure function with
$\Gamma \vdash \bot \le\alpha$
, as observed by Pierce (Reference Pierce1997). Simply extending the measure function with
![]() $\textit{size}_{\Psi}(\bot) = 1$
will not work. For type variables, the measure function will recursively look up its bound in the context and add one to the measure of its bound, making a variable equivalent to
$\textit{size}_{\Psi}(\bot) = 1$
will not work. For type variables, the measure function will recursively look up its bound in the context and add one to the measure of its bound, making a variable equivalent to
![]() $\bot$
to have a larger measure than
$\bot$
to have a larger measure than
![]() $\bot$
. Therefore, replacing two equivalent types into the abstracted type body may not produce the same measures. We can construct derivations of rule S-equivall that have a larger measure in the premise than that of the conclusion, which makes the decidability proof fail with the current measure. For example, consider the following subtyping derivation:
$\bot$
. Therefore, replacing two equivalent types into the abstracted type body may not produce the same measures. We can construct derivations of rule S-equivall that have a larger measure in the premise than that of the conclusion, which makes the decidability proof fail with the current measure. For example, consider the following subtyping derivation:

If we follow the measure function defined in Section 4.3, the measure for the third premise is:
while the measure for the goal is

which can be less than the measure of the premise since
![]() $\gamma$
is assigned a smaller measure in the goal. A similar issue arises when a variable is lower bounded by
$\gamma$
is assigned a smaller measure in the goal. A similar issue arises when a variable is lower bounded by
![]() $\top$
, making it equivalent to top types but with a different measure.
$\top$
, making it equivalent to top types but with a different measure.
This issue can be resolved by replacing all the types whose supertype is
![]() $\bot$
with
$\bot$
with
![]() $\bot$
, and all the types whose subtype is
$\bot$
, and all the types whose subtype is
![]() $\top$
with
$\top$
with
![]() $\top$
before computing the measure. That way, the subtyping relation
$\top$
before computing the measure. That way, the subtyping relation
![]() $\alpha \le \bot,~\beta \le \alpha \vdash \forall({\gamma}\le{\alpha}).{A} \le \forall({\gamma}\le{\beta}).{B}$
becomes
$\alpha \le \bot,~\beta \le \alpha \vdash \forall({\gamma}\le{\alpha}).{A} \le \forall({\gamma}\le{\beta}).{B}$
becomes
and the measure works again. This idea can be implemented by modifying the measure function to identify upper/lower bounded variables that are equivalent to bottom/top types, as can be seen in Figure 10. The new bindings
![]() $\alpha \mapsto \bot$
and
$\alpha \mapsto \bot$
and
![]() $\alpha \mapsto \top$
are used to store the measure of variables or indicate them as upper bounded by
$\alpha \mapsto \top$
are used to store the measure of variables or indicate them as upper bounded by
![]() $\bot$
or lower bounded by
$\bot$
or lower bounded by
![]() $\top$
. Figure 10 shows the measures needed for the decidability of
$\top$
. Figure 10 shows the measures needed for the decidability of
![]() $F_{\le\ge}^{\mu\wedge}$
. The primary measure function is
$F_{\le\ge}^{\mu\wedge}$
. The primary measure function is
![]() $\textit{size}_\Psi(A)$
. The main changes are in the cases for bounded quantification where we now use
$\textit{size}_\Psi(A)$
. The main changes are in the cases for bounded quantification where we now use
![]() $\textit{isTop}$
and
$\textit{isTop}$
and
![]() $\textit{isBot}$
functions to detect whether the bounds are, respectively, equivalent to top or bottom.
$\textit{isBot}$
functions to detect whether the bounds are, respectively, equivalent to top or bottom.

Fig. 10. The measures for the decidability of
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
The
![]() $\textit{isTop}$
and
$\textit{isTop}$
and
![]() $\textit{isBot}$
functions use the information in the measure context
$\textit{isBot}$
functions use the information in the measure context
![]() $\Psi$
to check whether the bound type A is equivalent to
$\Psi$
to check whether the bound type A is equivalent to
![]() $\top$
or
$\top$
or
![]() $\bot$
. If so, when the variable bounded by A is looked up in the context, it will have a measure of 1. The example above will now be resolved by the new measure function as follows:
$\bot$
. If so, when the variable bounded by A is looked up in the context, it will have a measure of 1. The example above will now be resolved by the new measure function as follows:

In this way, we retain the important property that equivalent types have the same measure.
Lemma 5.12. If
![]() $\Gamma \vdash A \le B$
and
$\Gamma \vdash A \le B$
and
![]() $\Gamma \vdash B \le A$
, then
$\Gamma \vdash B \le A$
, then
![]() $\textit{size}_{eval(\Gamma)}(A) = \textit{size}_{eval(\Gamma)}(B)$
in
$\textit{size}_{eval(\Gamma)}(A) = \textit{size}_{eval(\Gamma)}(B)$
in
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Note that in the proof of Lemma 5.12, in the case of intersection types, we make use of the compatibility relation
![]() $A \,\#\, B$
to ensure that any equivalent types have the same measure. Without the compatibility restriction, the labels may be duplicated within the intersection type, which will lead to a different measure for equivalent types. By limiting compatible types to single-field records and their intersections only, we also rule out the occurrence of
$A \,\#\, B$
to ensure that any equivalent types have the same measure. Without the compatibility restriction, the labels may be duplicated within the intersection type, which will lead to a different measure for equivalent types. By limiting compatible types to single-field records and their intersections only, we also rule out the occurrence of
![]() $\top$
in intersection types, which will cause the same problem. With the new measure function, we can prove the decidability of subtyping and typing in
$\top$
in intersection types, which will cause the same problem. With the new measure function, we can prove the decidability of subtyping and typing in
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Theorem 5.13 (Decidability of
![]() $F_{\le\ge}^{\mu\wedge}$
subtyping).
$F_{\le\ge}^{\mu\wedge}$
subtyping).
![]() $\Gamma \vdash A \le B$
is decidable in
$\Gamma \vdash A \le B$
is decidable in
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Theorem 5.14 (Decidability of
![]() $F_{\le\ge}^{\mu\wedge}$
typing).
$F_{\le\ge}^{\mu\wedge}$
typing).
![]() $\Gamma \vdash e : A$
is decidable in
$\Gamma \vdash e : A$
is decidable in
![]() $F_{\le\ge}^{\mu\wedge}$
.
$F_{\le\ge}^{\mu\wedge}$
.
Conservativity
The proof of conservativity for
![]() $F_{\le\ge}^{\mu\wedge}$
follows the same pattern as the proof for
$F_{\le\ge}^{\mu\wedge}$
follows the same pattern as the proof for
![]() $F_{\le}^{\mu}$
. To prove conservativity of typing, we need the help of the algorithmic typing rules to obtain the minimum type of an
$F_{\le}^{\mu}$
. To prove conservativity of typing, we need the help of the algorithmic typing rules to obtain the minimum type of an
![]() $F_{\le}$
term. We have defined the algorithmic typing rules for
$F_{\le}$
term. We have defined the algorithmic typing rules for
![]() $F_{\le\ge}^{\mu\wedge}$
and proved the completeness of the algorithmic typing rules in Section 5.2. With the algorithmic typing rules, conservativity for
$F_{\le\ge}^{\mu\wedge}$
and proved the completeness of the algorithmic typing rules in Section 5.2. With the algorithmic typing rules, conservativity for
![]() $F_{\le\ge}^{\mu\wedge}$
is straightforward.
$F_{\le\ge}^{\mu\wedge}$
is straightforward.
Theorem 5.15 (Conservativity for
![]() $F_{\le\ge}^{\mu\wedge}$
). If
$F_{\le\ge}^{\mu\wedge}$
). If
![]() $\Gamma$
, A, and e are well formed in
$\Gamma$
, A, and e are well formed in
![]() $F_{\le}$
, namely (1)
$F_{\le}$
, namely (1)
![]() $\vdash_F \Gamma$
(2)
$\vdash_F \Gamma$
(2)
![]() $\Gamma \vdash_F A$
and (3)
$\Gamma \vdash_F A$
and (3)
![]() $ \vdash_F e$
, then
$ \vdash_F e$
, then
![]() $\Gamma \vdash_F e : A$
if and only if
$\Gamma \vdash_F e : A$
if and only if
![]() $\Gamma \vdash e:A$
.
$\Gamma \vdash e:A$
.
6 Coq proofs
We develop and verify our formalization in Coq 8.13 (The Coq Development Team, 2021) and use Metalib to formalize variables and binders using the locally nameless representation (Aydemir et al., Reference Aydemir, Charguéraud, Pierce, Pollack and Weirich2008).
The Coq formalization is available online.Footnote
4
The directory “kernel_fsub_main” includes all definitions and proofs for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
described in Section 3, while the directory “full_fsub_main” includes the
$\textrm{kernel}~F_{\le}^{\mu}$
described in Section 3, while the directory “full_fsub_main” includes the
![]() $\textrm{full}~F_{\le}^{\mu}$
variant. Definition and proofs for
$\textrm{full}~F_{\le}^{\mu}$
variant. Definition and proofs for
![]() $F_{\le\ge}^{\mu\wedge}$
described in Section 5 are in the “kernel_fsub_ext” directory. Each directory can be checked independently, and the dependency of the proofs follows a sequential order in each directory.
$F_{\le\ge}^{\mu\wedge}$
described in Section 5 are in the “kernel_fsub_ext” directory. Each directory can be checked independently, and the dependency of the proofs follows a sequential order in each directory.
6.1 Definitions
All three systems share a similar structure for definitions: the files Rules.v contains the core definitions for the calculus, and AlgoTyping.v contains the algorithmic rules for typing. Tables 2, 3, and 4 show the correspondence between the paper definitions and the Coq formalization. The formalization mainly follows the definitions in the paper except for some technical details. One difference to note is that throughout the paper, we use only substitution to represent unfolding of a recursive type, application of universal quantification, and function abstraction. In the Coq proof, due to the use of the locally nameless representation, we also make use of the opening operation on pre-terms (Aydemir et al. Reference Aydemir, Charguéraud, Pierce, Pollack and Weirich2008). We also merge several rules for exposure and typing record expressions in the paper, for readability.
Table 2. Paper-to-proofs correspondence guide for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
(in kernel_fsub_main/ directory)
$\textrm{kernel}~F_{\le}^{\mu}$
(in kernel_fsub_main/ directory)
Table 3. Paper-to-proofs correspondence guide for
![]() $\textrm{full}~F_{\le}^{\mu}$
(in full_fsub_main/ directory). Definitions that are the same as
$\textrm{full}~F_{\le}^{\mu}$
(in full_fsub_main/ directory). Definitions that are the same as
![]() $\textrm{kernel}~F_{\le}^{\mu}$
are omitted
$\textrm{kernel}~F_{\le}^{\mu}$
are omitted

Table 4. Paper-to-proofs correspondence guide for
![]() $F_{\le\ge}^{\mu\wedge}$
(in kernel_fsub_ext/ directory)
$F_{\le\ge}^{\mu\wedge}$
(in kernel_fsub_ext/ directory)
6.2 Lemmas and theorems
Tables 5, 6, and 7 show the correspondence of lemmas and theorems between the paper and the Coq formalization. We provide the file location and theorem name in Coq for each lemma and theorem in the paper and include a brief description for each of them.
Table 5. Descriptions for the proof scripts for
![]() $\textrm{kernel}~F_{\le}^{\mu}$
(in kernel_fsub_main/ directory)
$\textrm{kernel}~F_{\le}^{\mu}$
(in kernel_fsub_main/ directory)

Table 6. Descriptions for the proof scripts for
![]() $\textrm{full}~F_{\le}^{\mu}$
(in full_fsub_main/ directory)
$\textrm{full}~F_{\le}^{\mu}$
(in full_fsub_main/ directory)

Table 7. Descriptions for the proof scripts for
![]() $F_{\le\ge}^{\mu\wedge}$
(in kernel_fsub_ext/ directory)
$F_{\le\ge}^{\mu\wedge}$
(in kernel_fsub_ext/ directory)
7 Related work
Throughout the paper, we have already reviewed some of the closest related work in detail. In this section, we discuss other related work.
7.1 Bounded quantification, recursive types, and object encodings
Bounded quantification was first introduced by Cardelli & Wegner (Reference Cardelli and Wegner1985) in the language Fun, where their kernel Fun calculus corresponds to the kernel version of
![]() $F_\le$
. The full variant of
$F_\le$
. The full variant of
![]() $F_{\le}$
was introduced by Curien & Ghelli (Reference Curien and Ghelli1992) and Cardelli et al. (Reference Cardelli, Martini, Mitchell and Scedrov1994), where the subtyping for bounds is contravariant. Although
$F_{\le}$
was introduced by Curien & Ghelli (Reference Curien and Ghelli1992) and Cardelli et al. (Reference Cardelli, Martini, Mitchell and Scedrov1994), where the subtyping for bounds is contravariant. Although
![]() $\textrm{full}~F_{\le}$
is powerful, subtyping proved to be undecidable (Pierce, Reference Pierce1994). As discussed in Section 1 there are several attempts to add recursive types to
$\textrm{full}~F_{\le}$
is powerful, subtyping proved to be undecidable (Pierce, Reference Pierce1994). As discussed in Section 1 there are several attempts to add recursive types to
![]() $F_{\le}$
, such as the work by Ghelli (Reference Ghelli1993), Colazzo & Ghelli (Reference Colazzo and Ghelli2005), and Jeffrey (Reference Jeffrey2001). Unfortunately, as Table 1 shows, such combinations are not painless, and even the successful combinations require significant changes for the subtyping rules. Ghelli (Reference Ghelli1993) illustrates how the combination of equi-recursive subtyping and
$F_{\le}$
, such as the work by Ghelli (Reference Ghelli1993), Colazzo & Ghelli (Reference Colazzo and Ghelli2005), and Jeffrey (Reference Jeffrey2001). Unfortunately, as Table 1 shows, such combinations are not painless, and even the successful combinations require significant changes for the subtyping rules. Ghelli (Reference Ghelli1993) illustrates how the combination of equi-recursive subtyping and
![]() $\textrm{full}~F_{\le}$
significantly alters the expressiveness of the subtyping relation. Specifically, he shows that there exist such subtyping relations
$\textrm{full}~F_{\le}$
significantly alters the expressiveness of the subtyping relation. Specifically, he shows that there exist such subtyping relations
![]() $A \nleq A'$
that do not hold in
$A \nleq A'$
that do not hold in
![]() $\textrm{full}~F_{\le}$
but are derivable when equi-recursive subtyping is added, by finding an intermediate type B which contains equi-recursive types such that
$\textrm{full}~F_{\le}$
but are derivable when equi-recursive subtyping is added, by finding an intermediate type B which contains equi-recursive types such that
![]() $A \le B$
and
$A \le B$
and
![]() $B \le A'$
. In Colazzo & Ghelli (Reference Colazzo and Ghelli2005)’s work, there is no independent universal type, and the shape of recursive types is either
$B \le A'$
. In Colazzo & Ghelli (Reference Colazzo and Ghelli2005)’s work, there is no independent universal type, and the shape of recursive types is either
![]() ${\mu{\alpha}}.{\forall({x}\le{A}).{B}}$
or
${\mu{\alpha}}.{\forall({x}\le{A}).{B}}$
or
![]() ${\mu{\alpha}}.{A\to B}$
. The recursive variables and universal variables are distinct, resulting in changes in environments and subtyping rules. For example, the subtyping environment is defined as
${\mu{\alpha}}.{A\to B}$
. The recursive variables and universal variables are distinct, resulting in changes in environments and subtyping rules. For example, the subtyping environment is defined as
![]() $\Pi := \cdot \mid \Pi, (x,y)\le (A,B) \mid \Pi, (\alpha=A, ~\beta=B)$
, and the S-vartrans rule of
$\Pi := \cdot \mid \Pi, (x,y)\le (A,B) \mid \Pi, (\alpha=A, ~\beta=B)$
, and the S-vartrans rule of
![]() $F_{\le}$
is changed to:
$F_{\le}$
is changed to:

The algorithm proposed by Jeffrey (Reference Jeffrey2001) is also complex and requires major changes. Both recursive variables and the subtyping algorithm are labeled with polarity modes, and the implementation of
![]() $\alpha$
-conversion is not discussed. In contrast, our subtyping rules do not change the contexts, the types are not restricted, and most importantly, we do not have to change the rules in the original
$\alpha$
-conversion is not discussed. In contrast, our subtyping rules do not change the contexts, the types are not restricted, and most importantly, we do not have to change the rules in the original
![]() $F_{\le}$
. This has the benefit that we can largely reuse the existing metatheory of the original
$F_{\le}$
. This has the benefit that we can largely reuse the existing metatheory of the original
![]() $F_{\le}$
, and it also enables our conservativity result. While it is plausible that Jeffrey (Reference Jeffrey2001)’s or Colazzo & Ghelli (Reference Colazzo and Ghelli2005)’s work for the
$F_{\le}$
, and it also enables our conservativity result. While it is plausible that Jeffrey (Reference Jeffrey2001)’s or Colazzo & Ghelli (Reference Colazzo and Ghelli2005)’s work for the
![]() $\textrm{kernel}~F_{\le}$
extensions with recursive types are conservative, this has not been proved. Furthermore, such proof is likely to be nontrivial because of the major changes introduced by equi-recursive subtyping.
$\textrm{kernel}~F_{\le}$
extensions with recursive types are conservative, this has not been proved. Furthermore, such proof is likely to be nontrivial because of the major changes introduced by equi-recursive subtyping.
There are many other extensions to
![]() $F_\le$
. Bounded existentials are also studied by Cardelli & Wegner (Reference Cardelli and Wegner1985). Existential types can be encoded by universal types; thus, we can obtain a form of bounded existentials for free in
$F_\le$
. Bounded existentials are also studied by Cardelli & Wegner (Reference Cardelli and Wegner1985). Existential types can be encoded by universal types; thus, we can obtain a form of bounded existentials for free in
![]() $F_\le$
(Cardelli & Wegner Reference Cardelli and Wegner1985). Another important extension is F-bounded quantification, first proposed by Canning et al. (Reference Canning, Cook, Hill and Olthoff1989), then studied by Baldan et al. (Reference Baldan, Ghelli and Raffaetà1999) in terms of the basic theory. In F-bounded quantification, the bounded variables are allowed to appear in the bound, denoted as
$F_\le$
(Cardelli & Wegner Reference Cardelli and Wegner1985). Another important extension is F-bounded quantification, first proposed by Canning et al. (Reference Canning, Cook, Hill and Olthoff1989), then studied by Baldan et al. (Reference Baldan, Ghelli and Raffaetà1999) in terms of the basic theory. In F-bounded quantification, the bounded variables are allowed to appear in the bound, denoted as
![]() $\forall({\alpha}\le{F[\alpha]}).{B}$
. We can encode polymorphic binary methods (Bruce et al., Reference Bruce, Cardelli, Castagna, Group, Leavens and Pierce1995) and methods that have recursive types in their signatures with F-bounded quantification. However, as we discussed in Section 2.2, for subtyping statements to satisfy the bound
$\forall({\alpha}\le{F[\alpha]}).{B}$
. We can encode polymorphic binary methods (Bruce et al., Reference Bruce, Cardelli, Castagna, Group, Leavens and Pierce1995) and methods that have recursive types in their signatures with F-bounded quantification. However, as we discussed in Section 2.2, for subtyping statements to satisfy the bound
![]() $\alpha \le F[\alpha]$
, they must be interpreted using equi-recursive subtyping, as F-bounds are normally records, and an iso-recursive type cannot be the subtype of a record type. F-bounded quantification is appealing because it can even deal with binary methods, where recursive types appear in negative positions. For example, with F-bounded quantification, we can model bounds such as
$\alpha \le F[\alpha]$
, they must be interpreted using equi-recursive subtyping, as F-bounds are normally records, and an iso-recursive type cannot be the subtype of a record type. F-bounded quantification is appealing because it can even deal with binary methods, where recursive types appear in negative positions. For example, with F-bounded quantification, we can model bounds such as
![]() $\alpha \le \{ x: \textsf{Int},~ \textsf{eq}: \alpha \to\textsf{Bool}\}$
and still have the expected subtyping relations.
$\alpha \le \{ x: \textsf{Int},~ \textsf{eq}: \alpha \to\textsf{Bool}\}$
and still have the expected subtyping relations.
Whereas we show that with the structural unfolding rule we can model positive cases of F-bounded quantification (such as translate) in
![]() $F_{\le}^{\mu}$
, we can only model a restricted form of negative F-bounded quantification. For instance, in
$F_{\le}^{\mu}$
, we can only model a restricted form of negative F-bounded quantification. For instance, in
![]() $F_{\le}^{\mu}$
we can have the bound
$F_{\le}^{\mu}$
we can have the bound
![]() $\alpha \le \mu{\textsf{P}}{\{x: \textsf{Int},~ \textsf{eq}: \textsf{P} \to \textsf{Bool}\}}$
and we can instantiate
$\alpha \le \mu{\textsf{P}}{\{x: \textsf{Int},~ \textsf{eq}: \textsf{P} \to \textsf{Bool}\}}$
and we can instantiate
![]() $\alpha$
with P (where
$\alpha$
with P (where
![]() $P = \mu{\textsf{P}}{\{ x:\textsf{Int},~ \textsf{eq}: \textsf{P} \to \textsf{Bool}\}}$
). However, we would not be able to instantiate
$P = \mu{\textsf{P}}{\{ x:\textsf{Int},~ \textsf{eq}: \textsf{P} \to \textsf{Bool}\}}$
). However, we would not be able to instantiate
![]() $\alpha$
with some types that have extra fields, such as
$\alpha$
with some types that have extra fields, such as
![]() $ {\mu {\textsf{P}}}$
’
$ {\mu {\textsf{P}}}$
’
![]() ${\{ x:\textsf{Int},~y: \textsf{Int}, \textsf{eq}: \textsf{P'} \to \textsf{Bool}\}}$
. In contrast, F-bounded quantification allows such forms of instantiation. Nevertheless, given the overlap between some of the applications of iso-recursive types in
${\{ x:\textsf{Int},~y: \textsf{Int}, \textsf{eq}: \textsf{P'} \to \textsf{Bool}\}}$
. In contrast, F-bounded quantification allows such forms of instantiation. Nevertheless, given the overlap between some of the applications of iso-recursive types in
![]() $F_{\le}^{\mu}$
and F-bounded quantification, we believe that it is worthwhile to investigate whether F-bounded quantification can be avoided to deal with general binary methods.
$F_{\le}^{\mu}$
and F-bounded quantification, we believe that it is worthwhile to investigate whether F-bounded quantification can be avoided to deal with general binary methods.
F-bounded quantification offers an elegant method for encoding objects that possess binary methods. When not seeking to fully encode binary methods, other object encodings are also available. Recursive records can encode objects (Cook et al., Reference Cook, Hill and Canning1989; Canning et al., Reference Canning, Cook, Hill and Olthoff1989; Bruce et al., Reference Bruce, Cardelli and Pierce1999). Alternatively, existential types can also be used to encode objects (Pierce & Turner, Reference Pierce and Turner1994), or they can be employed together with recursive types (Bruce, Reference Bruce1994). Pierce & Turner (Reference Pierce and Turner1994)’s object encoding using existential types is notable in that it requires only
![]() $F_{\le}$
and does not employ recursive types. The ORBE encoding (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996), as we discussed in Section 2.2, consists of recursive types, bounded existential quantification, records, and the structural unfolding rule. As Bruce et al. (Reference Bruce, Cardelli and Pierce1999) observe, the ORBE encoding requires
$F_{\le}$
and does not employ recursive types. The ORBE encoding (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996), as we discussed in Section 2.2, consists of recursive types, bounded existential quantification, records, and the structural unfolding rule. As Bruce et al. (Reference Bruce, Cardelli and Pierce1999) observe, the ORBE encoding requires
![]() $\textrm{full}~F_{\le}$
for the bounded quantification subtyping rule. When we try to compare two bounds, the type variable will be substituted with the existential types, which may result in bounds that are not equivalent. The overview paper by Bruce et al. (Reference Bruce, Cardelli and Pierce1999) makes a detailed comparison among different object encodings. Our
$\textrm{full}~F_{\le}$
for the bounded quantification subtyping rule. When we try to compare two bounds, the type variable will be substituted with the existential types, which may result in bounds that are not equivalent. The overview paper by Bruce et al. (Reference Bruce, Cardelli and Pierce1999) makes a detailed comparison among different object encodings. Our
![]() $F_{\le}^{\mu}$
calculus could act as a target for all those existing object encodings discussed above. To our best knowledge, a complete formalization of
$F_{\le}^{\mu}$
calculus could act as a target for all those existing object encodings discussed above. To our best knowledge, a complete formalization of
![]() $F_{\le}$
with recursive types, featuring desirable properties such as type soundness and conservativity, was not available at the time. Our work contributes to the validation of these encodings by offering a complete formalization of
$F_{\le}$
with recursive types, featuring desirable properties such as type soundness and conservativity, was not available at the time. Our work contributes to the validation of these encodings by offering a complete formalization of
![]() $F_{\le}$
with recursive types, along with several desirable properties.
$F_{\le}$
with recursive types, along with several desirable properties.
7.2 Dependent object types
The renewed interest in languages featuring bounded quantification and recursive types has been reignited recently within the research community, following the introduction of the dependent object types (DOT) calculus (Rompf & Amin, Reference Rompf and Amin2016). DOT is now the foundation of Scala 3 (EPFL 2021). The research on DOT has been intimately related to
![]() $F_{\le}$
. For instance, Amin & Rompf (Reference Amin and Rompf2017) explain many of the features of DOT by incrementally extending
$F_{\le}$
. For instance, Amin & Rompf (Reference Amin and Rompf2017) explain many of the features of DOT by incrementally extending
![]() $F_{\le}$
. DOT implements a generalized form of bounded quantification along with recursive types. This generalized form encompasses both upper and lower bounded quantification. Furthermore, DOT facilitates path selection that simultaneously supports upper and lower bounds. Additionally, DOT incorporates intersection types (Pottinger, Reference Pottinger1980; Coppo et al., Reference Coppo, Dezani-Ciancaglini and Venneri1981; Barbanera et al., Reference Barbanera, Dezani-Ciancaglini and de’Liguoro1995) for typing objects. A distinctive characteristic of DOT is its use of path-dependent types (Amin et al., Reference Amin, Rompf and Odersky2014). With path-dependent types, the treatment of recursive types is different from our calculus
$F_{\le}$
. DOT implements a generalized form of bounded quantification along with recursive types. This generalized form encompasses both upper and lower bounded quantification. Furthermore, DOT facilitates path selection that simultaneously supports upper and lower bounds. Additionally, DOT incorporates intersection types (Pottinger, Reference Pottinger1980; Coppo et al., Reference Coppo, Dezani-Ciancaglini and Venneri1981; Barbanera et al., Reference Barbanera, Dezani-Ciancaglini and de’Liguoro1995) for typing objects. A distinctive characteristic of DOT is its use of path-dependent types (Amin et al., Reference Amin, Rompf and Odersky2014). With path-dependent types, the treatment of recursive types is different from our calculus
![]() $F_{\le\ge}^{\mu\wedge}$
. In DOT, recursive types are introduced using recursive self types:
$F_{\le\ge}^{\mu\wedge}$
. In DOT, recursive types are introduced using recursive self types:
![]() $\{z \Rightarrow T^z\}$
. The variable z is a term variable. Thus, a recursive self type provides a limited form of dependent types, modeling a dependently typed fixpoint operator. In contrast, in
$\{z \Rightarrow T^z\}$
. The variable z is a term variable. Thus, a recursive self type provides a limited form of dependent types, modeling a dependently typed fixpoint operator. In contrast, in
![]() $F_{\le\ge}^{\mu\wedge}$
, the variable
$F_{\le\ge}^{\mu\wedge}$
, the variable
![]() $\alpha$
of a recursive type
$\alpha$
of a recursive type
![]() ${\mu{\alpha}}.{A}$
is a type variable. In
${\mu{\alpha}}.{A}$
is a type variable. In
![]() $F_{\le\ge}^{\mu\wedge}$
, the type of objects is similar to that in DOT: we employ intersections of the types of all the fields, and we require that the labels are disjoint. If the object uses recursive types, then we use a fold around the term.
$F_{\le\ge}^{\mu\wedge}$
, the type of objects is similar to that in DOT: we employ intersections of the types of all the fields, and we require that the labels are disjoint. If the object uses recursive types, then we use a fold around the term.
Previous attempts to prove the undecidability of DOT reduced the problem to the undecidability problem in
![]() $F_{\le}$
, relying on a translation from
$F_{\le}$
, relying on a translation from
![]() $F_{\le}$
to types in DOT (Rompf & Amin, Reference Rompf and Amin2016). However, as Hu & Lhoták (Reference Hu and Lhoták2020) later observed, the translation is not conservative. For example, in
$F_{\le}$
to types in DOT (Rompf & Amin, Reference Rompf and Amin2016). However, as Hu & Lhoták (Reference Hu and Lhoták2020) later observed, the translation is not conservative. For example, in
![]() $F_{\le}$
,
$F_{\le}$
,
![]() $\top \to \top \le \forall({\alpha}\le{\top}).{\top}$
is not a valid subtyping statement because function types and universal types are not comparable. However, after translating them into DOT, the statement becomes
$\top \to \top \le \forall({\alpha}\le{\top}).{\top}$
is not a valid subtyping statement because function types and universal types are not comparable. However, after translating them into DOT, the statement becomes
![]() $\forall (\alpha : \top).~\top \le \forall (\alpha : \{\top..\top\}).~\top$
, in which
$\forall (\alpha : \top).~\top \le \forall (\alpha : \{\top..\top\}).~\top$
, in which
![]() $\{\top..\top\}$
indicates that
$\{\top..\top\}$
indicates that
![]() $\alpha$
is both upper and lower bounded by
$\alpha$
is both upper and lower bounded by
![]() $\top$
. This statement is valid in DOT variants that allow full or equivalent subtyping for bounded quantification, which breaks the conservativity from
$\top$
. This statement is valid in DOT variants that allow full or equivalent subtyping for bounded quantification, which breaks the conservativity from
![]() $F_{\le}$
to DOT. Nevertheless, Hu & Lhoták (Reference Hu and Lhoták2020) showed that the undecidability of DOT can be reduced to an undecidable fragment
$F_{\le}$
to DOT. Nevertheless, Hu & Lhoták (Reference Hu and Lhoták2020) showed that the undecidability of DOT can be reduced to an undecidable fragment
![]() $F_{\le}^{-}$
of full
$F_{\le}^{-}$
of full
![]() $F_{\le}$
, that excludes the function types, and proved that DOT is undecidable.
$F_{\le}$
, that excludes the function types, and proved that DOT is undecidable.
There are two notable decidable variants of DOT: the strong kernel
![]() $D_{<:}$
calculus from Hu & Lhoták (Reference Hu and Lhoták2020) and the Wyvern language by Mackay et al., (Reference Mackay, Potanin, Aldrich and Groves2020). These systems share features akin to
$D_{<:}$
calculus from Hu & Lhoták (Reference Hu and Lhoták2020) and the Wyvern language by Mackay et al., (Reference Mackay, Potanin, Aldrich and Groves2020). These systems share features akin to
![]() $F_{\le\ge}^{\mu\wedge}$
, making comparisons worthwhile. As variants of DOT, both support path-dependent types. The decidable variant by Hu & Lhoták (Reference Hu and Lhoták2020) selects specific features from DOT, including upper and lower bounds for path selection, and an equivalent subtyping quantifier for
$F_{\le\ge}^{\mu\wedge}$
, making comparisons worthwhile. As variants of DOT, both support path-dependent types. The decidable variant by Hu & Lhoták (Reference Hu and Lhoták2020) selects specific features from DOT, including upper and lower bounds for path selection, and an equivalent subtyping quantifier for
![]() $F_{\le}$
, but it lacks recursive and intersection types. To handle the complexity of path types in proof of decidability, they define an algorithmic version of the subtyping rules, called stare-at subtyping, prove its equivalence to the declarative rules, and use a simple measure to show that the algorithmic rules terminate. The system developed by Mackay et al. (Reference Mackay, Potanin, Aldrich and Groves2020) shares several similarities with
$F_{\le}$
, but it lacks recursive and intersection types. To handle the complexity of path types in proof of decidability, they define an algorithmic version of the subtyping rules, called stare-at subtyping, prove its equivalence to the declarative rules, and use a simple measure to show that the algorithmic rules terminate. The system developed by Mackay et al. (Reference Mackay, Potanin, Aldrich and Groves2020) shares several similarities with
![]() $F_{\le\ge}^{\mu\wedge}$
, including the enforcement of comparable constraints on bounds and the integration of a restricted version of intersection types for typing objects. However, it distinguishes itself by using equi-recursive types for recursion.
$F_{\le\ge}^{\mu\wedge}$
, including the enforcement of comparable constraints on bounds and the integration of a restricted version of intersection types for typing objects. However, it distinguishes itself by using equi-recursive types for recursion.
Reflecting on the complexity inherent in full intersection types, Mackay et al. (Reference Mackay, Potanin, Aldrich and Groves2020) also adopt a restricted form of these types to refine recursive objects. To ensure decidability, their methodology employs a kernel variant of
![]() $F_{\le}$
. As for the proof of decidability, Mackay et al. (Reference Mackay, Potanin, Aldrich and Groves2020) define type graphs, a graphical representation of types, and type declarations, along with the dependency information between them. They provide a general algorithm for checking type graph subtyping and show that in the restricted system, all types are homomorphic to type graphs that obey the material/shape separation property, which ensures that the subtyping algorithm terminates. In contrast, the decidability proof for
$F_{\le}$
. As for the proof of decidability, Mackay et al. (Reference Mackay, Potanin, Aldrich and Groves2020) define type graphs, a graphical representation of types, and type declarations, along with the dependency information between them. They provide a general algorithm for checking type graph subtyping and show that in the restricted system, all types are homomorphic to type graphs that obey the material/shape separation property, which ensures that the subtyping algorithm terminates. In contrast, the decidability proof for
![]() $F_{\le\ge}^{\mu\wedge}$
does not rely on alternative subtyping rules or type representations and is solely based on measures. Both decidable systems in DOT incorporate top and bottom types and have been demonstrated to be reflexive, similar to
$F_{\le\ge}^{\mu\wedge}$
does not rely on alternative subtyping rules or type representations and is solely based on measures. Both decidable systems in DOT incorporate top and bottom types and have been demonstrated to be reflexive, similar to
![]() $F_{\le\ge}^{\mu\wedge}$
. However, one of the limitations of DOT is that transitivity elimination is not possible (Rompf & Amin, Reference Rompf and Amin2016), and even the two decidable fragments of DOT lack transitivity (Hu & Lhoták, Reference Hu and Lhoták2020; Mackay et al., Reference Mackay, Potanin, Aldrich and Groves2020). In contrast, in
$F_{\le\ge}^{\mu\wedge}$
. However, one of the limitations of DOT is that transitivity elimination is not possible (Rompf & Amin, Reference Rompf and Amin2016), and even the two decidable fragments of DOT lack transitivity (Hu & Lhoták, Reference Hu and Lhoták2020; Mackay et al., Reference Mackay, Potanin, Aldrich and Groves2020). In contrast, in
![]() $F_{\le\ge}^{\mu\wedge}$
transitivity can be derived from the subtyping rules.
$F_{\le\ge}^{\mu\wedge}$
transitivity can be derived from the subtyping rules.
While
![]() $F_{\le\ge}^{\mu\wedge}$
does not have all the features of DOT, our results can potentially help in research in that area, where the decidable fragments of DOT lack important properties such as transitivity. In addition,
$F_{\le\ge}^{\mu\wedge}$
does not have all the features of DOT, our results can potentially help in research in that area, where the decidable fragments of DOT lack important properties such as transitivity. In addition,
![]() $F_{\le\ge}^{\mu\wedge}$
preserves the conservativity over
$F_{\le\ge}^{\mu\wedge}$
preserves the conservativity over
![]() $\textrm{kernel}~F_{\le}$
, while DOT does not. Table 8 presents a comparative analysis of the four calculi.
$\textrm{kernel}~F_{\le}$
, while DOT does not. Table 8 presents a comparative analysis of the four calculi.
Table 8. Comparison
![]() $F_{\le\ge}^{\mu\wedge}$
with DOT and its variants
$F_{\le\ge}^{\mu\wedge}$
with DOT and its variants

7.3 Algebraic datatypes and subtyping
Algebraic datatypes are a fundamental feature in modern functional programming languages, such as Haskell (Haskell Development Team, 1990) and OCaml (INRIA, 1987). However, such languages do not support subtyping between datatypes. Hosoya et al. (unpublished data) discussed the interaction between mutually recursive datatypes and subtyping. They presented two variants of
![]() $F_{\le}$
extending
$F_{\le}$
extending
![]() $F_{\le}$
with user-defined datatype declarations. The first variant has user-defined subtyping declarations between datatypes and can be viewed as having a form of nominal subtyping. The second variant allows structural subtyping among the datatypes.
$F_{\le}$
with user-defined datatype declarations. The first variant has user-defined subtyping declarations between datatypes and can be viewed as having a form of nominal subtyping. The second variant allows structural subtyping among the datatypes.
One advantage of employing user-defined datatypes is that it is simple to deal with formally, and that it allows mutually recursive datatype definitions easily. However, they do not support conventional recursive types of the form
![]() ${\mu{\alpha}}.{A}$
as we do in
${\mu{\alpha}}.{A}$
as we do in
![]() $F_{\le}^{\mu}$
. Moreover, they do not consider lower bounded quantification which, as argued in Section 2.2, seems to be quite useful in a system targeting algebraic datatypes.
$F_{\le}^{\mu}$
. Moreover, they do not consider lower bounded quantification which, as argued in Section 2.2, seems to be quite useful in a system targeting algebraic datatypes.
More recently, Rossberg (Reference Rossberg2023) proposed another calculus with a similar idea of using declared subtyping for recursive types, aiming at providing better and more efficient support for mutually recursive datatypes in type-safe low-level languages like Wasm. In their work, recursive types take the form
![]() $\mu\langle\alpha_1\le A_1,\alpha_2\le A_2\rangle.\,B$
, where the declared bound
$\mu\langle\alpha_1\le A_1,\alpha_2\le A_2\rangle.\,B$
, where the declared bound
![]() $A_2$
can refer to
$A_2$
can refer to
![]() $\alpha_1$
so that two mutually recursive types can be defined at once. This avoids the polynomial explosion of encoding mutual recursion using single recursion à la Bekić’s Lemma (Bekić, 2005). However, to deal with type bounds in the
$\alpha_1$
so that two mutually recursive types can be defined at once. This avoids the polynomial explosion of encoding mutual recursion using single recursion à la Bekić’s Lemma (Bekić, 2005). However, to deal with type bounds in the
![]() $\mu$
-operator, they need to employ higher-order subtyping (Pierce & Steffen, Reference Pierce and Steffen1997).
$\mu$
-operator, they need to employ higher-order subtyping (Pierce & Steffen, Reference Pierce and Steffen1997).
There has been some work integrating ML datatypes and OO classes (Bourdoncle & Merz, Reference Bourdoncle and Merz1997; Millstein et al., Reference Millstein, Bleckner and Chambers2004). In the implementation of hierarchical extensible datatypes, methods are simulated via functions with dynamic dispatch. Those works are focused on the design of intermediate languages that have complex constructs such as classes or datatypes. In contrast, we develop foundational calculi, where more complex constructs can be encoded. Finally, Poll (Reference Poll1998) investigated the categorical semantics of datatypes with subtyping and a limited form of inheritance on datatypes, improving our understanding of the relation between categorical datatypes and object types.
Oliveira (Reference Oliveira2009) showed encodings of algebraic datatypes with subtyping assuming a variant of
![]() $F_{\le}$
extended with records, recursive types, and higher kinds. He showed that adding subtyping to datatypes allows for solving the Expression Problem (Wadler, Reference Wadler1998). However, as we mentioned in Section 2.2, he did not formalize the
$F_{\le}$
extended with records, recursive types, and higher kinds. He showed that adding subtyping to datatypes allows for solving the Expression Problem (Wadler, Reference Wadler1998). However, as we mentioned in Section 2.2, he did not formalize the
![]() $F_{\le}$
extension, although he showed a translation of the encoding into Scala. Moreover, his encoding is more complex than ours because he employs upper bounded quantification with higher kinds. In Section 2.2, we showed that first-order lower bounded quantification in
$F_{\le}$
extension, although he showed a translation of the encoding into Scala. Moreover, his encoding is more complex than ours because he employs upper bounded quantification with higher kinds. In Section 2.2, we showed that first-order lower bounded quantification in
![]() $F_{\le\ge}^{\mu\wedge}$
, together with the structural folding rule, enables such encodings. As for encodings of objects, our work is helpful in further validating such encodings formally.
$F_{\le\ge}^{\mu\wedge}$
, together with the structural folding rule, enables such encodings. As for encodings of objects, our work is helpful in further validating such encodings formally.
8 Conclusion
Recursive types and bounded quantification play a significant role in various programming languages. While these features have been extensively studied individually, their combined interaction has remained a challenging problem for a long time. Our
![]() $F_{\le}^{\mu}$
calculus demonstrates a method for integrating iso-recursive types with two variations of
$F_{\le}^{\mu}$
calculus demonstrates a method for integrating iso-recursive types with two variations of
![]() $F_{\le}$
. We achieve a transitive and decidable subtyping relation for the kernel variant, and both calculi maintain conservativity over
$F_{\le}$
. We achieve a transitive and decidable subtyping relation for the kernel variant, and both calculi maintain conservativity over
![]() $F_{\le}$
and are type sound.
$F_{\le}$
and are type sound.
![]() $F_{\le}^{\mu}$
and
$F_{\le}^{\mu}$
and
![]() $F_{\le\ge}^{\mu\wedge}$
could provide a theoretical basis for object encodings and subtyping in algebraic datatypes. In particular, the
$F_{\le\ge}^{\mu\wedge}$
could provide a theoretical basis for object encodings and subtyping in algebraic datatypes. In particular, the
![]() $\textrm{full}~F_{\le}^{\mu}$
we have studied in this paper provides a foundation for the ORBE object encoding (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996). Recently, there has been a renewed interest in recursive types and bounded quantification, sparked by the DOT calculus. Our research helps in identifying calculi that include most features found in DOT, while preserving properties such as subtyping’s decidability and transitivity, or even conservativity over
$\textrm{full}~F_{\le}^{\mu}$
we have studied in this paper provides a foundation for the ORBE object encoding (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996). Recently, there has been a renewed interest in recursive types and bounded quantification, sparked by the DOT calculus. Our research helps in identifying calculi that include most features found in DOT, while preserving properties such as subtyping’s decidability and transitivity, or even conservativity over
![]() $F_{\le}$
. Exploring extensions of
$F_{\le}$
. Exploring extensions of
![]() $F_{\le}^{\mu}$
to include more features from DOT constitutes an interesting direction for future research.
$F_{\le}^{\mu}$
to include more features from DOT constitutes an interesting direction for future research.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0956796825000036
Conflicts of Interest
None.



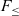
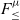
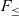
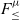
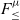
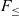
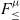
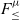
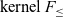
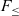

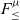
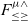
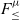
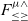





































Discussions
No Discussions have been published for this article.