1 Introduction
(…) A special feature of our approach is a general calculus of relations presented in part two. This calculus offers another, often more amenable framework for concepts and methods discussed in part one.
— Freyd & Ščedrov, Categories, Allegories, 1990.
Functions are mathematical objects, and functional programming (FP) has benefitted much from its strong mathematical foundations over the years. This began with LISP, a programming language born in the late 1950s that implemented Church’s
![]() ${\lambda }$
-calculus and included higher-order functions, that is, functions that manipulate other functions. This soon proved to be a strong competitive advantage.
${\lambda }$
-calculus and included higher-order functions, that is, functions that manipulate other functions. This soon proved to be a strong competitive advantage.
Another significant advantage, originally also identified by Church, is parametric polymorphism, a powerful device of great practical and theoretical relevance (Damas & Milner, Reference Damas and Milner1982). Pragmatically, it leads to a programming style in which programs are generic and can be better statically checked, adding to programming productivity since one writes less and better code — “programs for cheap!” in the words of Hackett & Hutton (Reference Hackett and Hutton2015). This comes hand in hand with another advantage, evident when one needs to reason about programs: parametricity theory ensures structural properties of functional code that need not be proved case by case — cf. the “theorem for free” motto coined by Wadler (Reference Wadler1989). Thus correctness-proving becomes more productive as well.
Curiously enough, parametricity theory found an effective formulation in terms of relations and not just functions (Reynolds, Reference Reynolds1983).As Janis Voigtländer (Reference Voigtländer2019) puts it, the key to deriving free theorems is to interpret types as relations. Indeed, it often happens in mathematics that, to better address a concept, it is convenient to invest into another one of wider scope. For example, the laws of basic trigonometry are best formulated if the domain of discourse is extended from real to complex numbers — recall Euler’s formula
![]() $e^{ix} = \cos x + i\sin x$
and all that follows from it. The same happens between functions and relations, the latter extending the former. The quote by Freyd & Scedrov (Reference Freyd and Scedrov1990) that opens this paper reveals exactly this, at the categorial level.
$e^{ix} = \cos x + i\sin x$
and all that follows from it. The same happens between functions and relations, the latter extending the former. The quote by Freyd & Scedrov (Reference Freyd and Scedrov1990) that opens this paper reveals exactly this, at the categorial level.
Building on this perspective, Bird & de Moor (Reference Bird and de Moor1997) developed an algebra of programming in which specifications (relations) lead to implementations (functions) by calculation. However, the application of relational techniques to FP is actually wider, see e.g. the work by Backhouse & Backhouse (Reference Backhouse and Backhouse2004) among much other research reported in the literature. This paper will follow the same path of using relations to reason about functional programs, taking a rather pragmatic view inspired by experience in the classroom.
Teaching FP is not an easy task, all the more so when it comes late in the syllabus, after imperative and object-oriented programming. FP calls for a plan of the overall architecture before starting writing code, with particular emphasis on designing a suitable information flow.Footnote 1 It is therefore important to help programmers in identifying “big picture” design patterns.
It can be claimed that the higher-order combinators so much used in FP enable design patterns for free by inter-combination — see e.g. map-filter, MapReduce (Lämmel, Reference Lämmel2008) and so on. In this paper we propose what we call “magic squares” (MS) to expand that view by expressing and composing quite common relational (and functional) patterns that arise in problem analysis and modeling.
Among several examples given in the paper, free-theorem MS prove to be elegant and productive. As observed by Voigtländer (Reference Voigtländer, Shao and Pierce2009), free theorems promise a lot but deriving them is not immediate. It is error-prone and can be tedious and result in intricate logical formulæ hard to simplify into something short and effective, even when using a mechanised generator. We claim that relational reasoning can be of great help in this respect. In this paper, free theorems are expressed in terms of magic squares, whose graphical nature makes it easier to perceive what is going on in the reasoning.
As an example of application, a generic, induction-free theory for
![]() ${\mathsf{foldr}{}{}}$
and
${\mathsf{foldr}{}{}}$
and
![]() ${\mathsf{foldl}{}{}}$
is given — understood in a class wider than just finite listsFootnote
2
— showing in particular that
${\mathsf{foldl}{}{}}$
is given — understood in a class wider than just finite listsFootnote
2
— showing in particular that
![]() ${\mathsf{foldl} \, {{s}}{}\mathrel{=}\mathsf{foldr}{({flip }\unicode{x005F}{s})}{}}$
holds under conditions milder than usually advocated.
${\mathsf{foldl} \, {{s}}{}\mathrel{=}\mathsf{foldr}{({flip }\unicode{x005F}{s})}{}}$
holds under conditions milder than usually advocated.
2 “Magic” squares
Experience in teaching FP using a relational approach has led the author to a graphical style of expression and reasoning in which a very simple, geometric construct shines: the (semi) commutative square.
In the classroom this is termed the “magic square” (MS), because much of what we do in logic, FP, database modeling, formal semantics, etc fits in some MS geometry. Each magic square has four sides, say R, P, S, Q, which are binary relations, and each square is a comparison between two paths, of two relations each:

In more detail, each side is an arrow, say ![]() , declaring a binary relation R that relates objects of types A and B. Its meaning is as usual: given objects
, declaring a binary relation R that relates objects of types A and B. Its meaning is as usual: given objects
![]() ${{a}\;\mathbin\in \;{A}}$
and
${{a}\;\mathbin\in \;{A}}$
and
![]() ${{b}\;\mathbin\in \;{B}}$
, the proposition
${{b}\;\mathbin\in \;{B}}$
, the proposition
![]() ${{a}\;{R}\;{b}}$
tells whether or not a and b are related by R. Take for instance relation
${{a}\;{R}\;{b}}$
tells whether or not a and b are related by R. Take for instance relation ![]() . Clearly,
. Clearly,
![]() ${\mathrm{0}\leq \mathrm{1}}$
holds (it is a true proposition) while
${\mathrm{0}\leq \mathrm{1}}$
holds (it is a true proposition) while
![]() ${\mathrm{1}\leq \mathrm{0}}$
does not.
${\mathrm{1}\leq \mathrm{0}}$
does not.
Next, we need to say what a path means, say
![]() ${{P} \cdot {R}}$
in (2.1): given some
${{P} \cdot {R}}$
in (2.1): given some
![]() ${{c}\;\mathbin\in \;{C}}$
and some
${{c}\;\mathbin\in \;{C}}$
and some
![]() ${{b}\;\mathbin\in \;{B}}$
,
${{b}\;\mathbin\in \;{B}}$
,
![]() ${{c}\;({P} \cdot {R})\;{b}}$
holds whenever there is some mediator
${{c}\;({P} \cdot {R})\;{b}}$
holds whenever there is some mediator
![]() ${{a}\;\mathbin\in \;{A}}$
such that both
${{a}\;\mathbin\in \;{A}}$
such that both
![]() ${{c}\;{P}\;{a}}$
and
${{c}\;{P}\;{a}}$
and
![]() ${{a}\;{R}\;{b}}$
hold. We say that relation
${{a}\;{R}\;{b}}$
hold. We say that relation
![]() ${{P} \cdot {R}}$
is the composition of relations
${{P} \cdot {R}}$
is the composition of relations
![]() ${{P}}$
and
${{P}}$
and
![]() ${{R}}$
. Relational composition is associative.
${{R}}$
. Relational composition is associative.
Finally, let us say what the comparison
![]() ${{R}\; \subseteq \;{S}}$
of two relations
${{R}\; \subseteq \;{S}}$
of two relations ![]() means, in general. (
means, in general. (
![]() ${{R}\; \subseteq \;{S}}$
should be read: “
${{R}\; \subseteq \;{S}}$
should be read: “
![]() ${{R}}$
is at most
${{R}}$
is at most
![]() ${{S}}$
” or “
${{S}}$
” or “
![]() ${{R}}$
is included in
${{R}}$
is included in
![]() ${{S}}$
”.) It means that, for all
${{S}}$
”.) It means that, for all
![]() ${{b}\;\mathbin\in \;{B}}$
and
${{b}\;\mathbin\in \;{B}}$
and
![]() ${{a}\;\mathbin\in \;{A}}$
, if
${{a}\;\mathbin\in \;{A}}$
, if
![]() ${{b}\;{R}\;{a}}$
holds then
${{b}\;{R}\;{a}}$
holds then
![]() ${{b}\;{S}\;{a}}$
holds too. In summary, relation inclusion “hides” a universal quantifier, while relation composition hides an existential quantifier. In symbols, the logic interpretation of (2.1) is:
${{b}\;{S}\;{a}}$
holds too. In summary, relation inclusion “hides” a universal quantifier, while relation composition hides an existential quantifier. In symbols, the logic interpretation of (2.1) is:
The following version of (2.2) makes its connection with (2.1) more explicit:

Comparisons
![]() ${{R}\; \subseteq \;{S}}$
form a partial order, and therefore are reflexive, transitive, and antisymmetric.
${{R}\; \subseteq \;{S}}$
form a partial order, and therefore are reflexive, transitive, and antisymmetric.
As will be shown shortly, one can express “a lot” using the “magic” square pattern (2.1), rendered pointwise in (2.2). Some terminology before giving examples: we shall refer to
![]() ${{R}\; \subseteq \;{S}}$
as a relational inequality in which
${{R}\; \subseteq \;{S}}$
as a relational inequality in which
![]() ${{R}}$
is the pre (or lower) side and
${{R}}$
is the pre (or lower) side and
![]() ${{S}}$
is the post (or upper) side. In a composition
${{S}}$
is the post (or upper) side. In a composition
![]() ${{R} \cdot {S}}$
, relation
${{R} \cdot {S}}$
, relation
![]() ${{S}}$
(resp.
${{S}}$
(resp.
![]() ${{R}}$
) will be referred to as the producer (resp. consumer) relation. This terminology bears some relationship to the way information flows in a magic square, cf.
${{R}}$
) will be referred to as the producer (resp. consumer) relation. This terminology bears some relationship to the way information flows in a magic square, cf.

Magic squares compose, not only horizontally

but also vertically:

Every type
![]() ${{X}}$
has its own identity relation
${{X}}$
has its own identity relation ![]() , which is such that
, which is such that
![]() ${{x'}\;{id}\;{x}~\Leftrightarrow~{x'}\mathrel{=}~{x}}$
. Therefore,
${{x'}\;{id}\;{x}~\Leftrightarrow~{x'}\mathrel{=}~{x}}$
. Therefore,
![]() ${{R} \cdot {id}\mathrel{=}{R}\mathrel{=}{id} \cdot {R}}$
holds for any R and thus squares involving id degenerate into triangles or even “sides”. So, squares in which both pre-consumer and post-producer are identities behave like units of square composition, cf.:
${{R} \cdot {id}\mathrel{=}{R}\mathrel{=}{id} \cdot {R}}$
holds for any R and thus squares involving id degenerate into triangles or even “sides”. So, squares in which both pre-consumer and post-producer are identities behave like units of square composition, cf.:

3 Functions
Statements like John loves Mary can be written as Mary is loved by John without changing meaning. The latter version is known as the passive voice of the former. Generalizing, any proposition
![]() ${{b}\;{R}\;{a}}$
can be converted to passive voice, written
${{b}\;{R}\;{a}}$
can be converted to passive voice, written
![]() ${{a}\;{{R}}^\circ\;{b}}$
. (In the example,
${{a}\;{{R}}^\circ\;{b}}$
. (In the example,
![]() ${{{loves}}^\circ\mathrel{=}{is}\;{loved}\;{by}}$
.) The
${{{loves}}^\circ\mathrel{=}{is}\;{loved}\;{by}}$
.) The
![]() ${{(_{\unicode{x2014}})}}^\circ$
operator, known as relational converse, will play a major role in our setting.
${{(_{\unicode{x2014}})}}^\circ$
operator, known as relational converse, will play a major role in our setting.
Converse is involutive (
![]() ${{({{R}^\circ})^\circ}\mathrel{=}{R}}$
) and contravariant:
${{({{R}^\circ})^\circ}\mathrel{=}{R}}$
) and contravariant:
![]() ${{({R} \cdot {S})^\circ}\mathrel{=}{{S}}^\circ \cdot {{R}}}^\circ$
. So one can take the converse of a square, obtaining an equivalent square where producer and consumer relations swap roles, once conversed:
${{({R} \cdot {S})^\circ}\mathrel{=}{{S}}^\circ \cdot {{R}}}^\circ$
. So one can take the converse of a square, obtaining an equivalent square where producer and consumer relations swap roles, once conversed:

Some relations, termed functions and denoted in lowercase — see e.g. f in (3.1) below — are special in the sense of fitting in two particular squares involving them and their converses:

By (2.2), the square on the left (
![]() ${{id}\; \subseteq \;{{f}}^\circ \cdot {f}}$
) converts to:
${{id}\; \subseteq \;{{f}}^\circ \cdot {f}}$
) converts to:
In words,
![]() ${{f}}$
reacts to every possible input (it is “total”). Similarly, the square on the right (
${{f}}$
reacts to every possible input (it is “total”). Similarly, the square on the right (
![]() ${{f} \cdot {{f}}^\circ\; \subseteq \;{id}}$
) converts to:
${{f} \cdot {{f}}^\circ\; \subseteq \;{id}}$
) converts to:
In words:
![]() ${{f}}$
is univocal. Because
${{f}}$
is univocal. Because
![]() ${{f}}$
in (3.1) always yields some output for any possible input, and such an output is unique, one can interpret the proposition
${{f}}$
in (3.1) always yields some output for any possible input, and such an output is unique, one can interpret the proposition
![]() ${{b}\;{f}\;{a}}$
as
${{b}\;{f}\;{a}}$
as
![]() ${{b}\mathrel{=}{f}\;{a}}$
, that is,
${{b}\mathrel{=}{f}\;{a}}$
, that is,
![]() ${{b}}$
is unequivocally the output of
${{b}}$
is unequivocally the output of
![]() ${{f}}$
once
${{f}}$
once
![]() ${{a}}$
is passed as input. This saves one from the two existential quantifiers of a very frequent and useful pattern involving functions and function converses:Footnote
3
${{a}}$
is passed as input. This saves one from the two existential quantifiers of a very frequent and useful pattern involving functions and function converses:Footnote
3

We shall refer to (3.2) as the “nice” rule, where
![]() ${{f}}$
and
${{f}}$
and
![]() ${{g}}$
are functions and
${{g}}$
are functions and
![]() ${{R}}$
is not constrained.Footnote
4
${{R}}$
is not constrained.Footnote
4
It can be shown that functions — i.e. relations
![]() ${{f}}$
fitting in (3.1) — are precisely those that satisfy the following square equivalences,
${{f}}$
fitting in (3.1) — are precisely those that satisfy the following square equivalences,
cf.

— similarly for (3.4). These equivalences, known as “shunting rules,” are very useful for reasoning about functions. One particular follow-up is that comparing functions amounts to equating them,
as can be easily shown:

4 Reynolds squares
In the sequel, we shall be particularly interested in squares (2.1) in which both pre-consumers and post-producers are functions, say
![]() ${{f}}$
and
${{f}}$
and
![]() ${{g}}$
in (4.1) given next:
${{g}}$
in (4.1) given next:

By (3.3) followed by the “nice rule” (3.2), square (4.1) captures the situation in which, for
![]() ${{R}}$
-related inputs, the two functions
${{R}}$
-related inputs, the two functions
![]() ${{f}}$
and
${{f}}$
and
![]() ${{g}}$
always yield
${{g}}$
always yield
![]() ${{S}}$
-related outputs: if
${{S}}$
-related outputs: if
![]() ${{a}\;{R}\;{b}}$
holds then
${{a}\;{R}\;{b}}$
holds then
![]() ${({f}\;{a})\;{S}\;({g}\;{b})}$
holds, for any
${({f}\;{a})\;{S}\;({g}\;{b})}$
holds, for any
![]() ${{a}}$
and
${{a}}$
and
![]() ${{b}}$
.
${{b}}$
.
We shall refer to squares of pattern (4.1) as Reynolds squares because of the role they will play in expressing free theorems of parametric polymorphic functions, due to John Reynolds (Reference Reynolds1983) and made popular by Philip Wadler (Reference Wadler1989). Note however that pattern (4.1) can be found in far more mundane settings, for instance relational database modeling.
Take for instance the very simple data model below of a small grocery in which customers can use coupons to obtain discounts when purchasing goods:

The “polygons” of the data model can be regarded as “opportunities” to dig up business rules, i.e. data invariants. Indeed, the triangle on the right can be oriented as the square

which is indeed meaningful: coupons cannot be used beyond their expiry date. And the lefthand triangle can be oriented as

bearing in it another relevant business rule: coupons can only be used by the customers who own them. Footnote 5
Squares in general (2.1) arise naturally in formal modeling in various guises, involving data relations (e.g. key-value maps), object attributes etc, and capturing not only domain-specific invariants such as those illustrated above but also structural ones. Particularly frequent squares are those that capture referential integrity,

where
![]() ${\top }$
is the largest relation of its type, that is,
${\top }$
is the largest relation of its type, that is, ![]() for all
for all
![]() ${{b}}$
and
${{b}}$
and
![]() ${{k}}$
. Think of
${{k}}$
. Think of
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
as key-value stores with keys
${{S}}$
as key-value stores with keys
![]() ${{K}}$
and
${{K}}$
and
![]() ${{K'}}$
, respectively, the latter playing the role of foreign key referred to by attribute
${{K'}}$
, respectively, the latter playing the role of foreign key referred to by attribute
![]() ${{f}}$
of
${{f}}$
of
![]() ${{A}}$
(a function).Footnote
6
${{A}}$
(a function).Footnote
6
Reynolds arrow Back to the genericity of Reynolds squares, fix the pre-producer
![]() ${{R}}$
and the post-consumer
${{R}}$
and the post-consumer
![]() ${{S}}$
of (4.1). Then (4.1) expresses a (higher-order) relation on functions
${{S}}$
of (4.1). Then (4.1) expresses a (higher-order) relation on functions
![]() ${{f}\;({R}\to {S})\;{g}}$
defined by:
${{f}\;({R}\to {S})\;{g}}$
defined by:
Usinghe exponential notation
![]() ${{{Y}}^{{X}}}$
to denote the type of all functions from type
${{{Y}}^{{X}}}$
to denote the type of all functions from type
![]() ${{X}}$
to type
${{X}}$
to type
![]() ${{Y}}$
, and extending it to relations,
${{Y}}$
, and extending it to relations,
![]() ${{{S}}^{{R}}\mathrel{=}({R}\to {S})}$
, one has:
${{{S}}^{{R}}\mathrel{=}({R}\to {S})}$
, one has:

Thus we obtain the Reynolds arrow, a higher-order relational operator that builds, from relations
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
, the (higher-order) relation
${{S}}$
, the (higher-order) relation
![]() ${{{S}}^{{R}}}$
on functions identified by Backhouse (Reference Backhouse1990) and defined above by (4.5). We will use the notations
${{{S}}^{{R}}}$
on functions identified by Backhouse (Reference Backhouse1990) and defined above by (4.5). We will use the notations
![]() ${{{S}}^{{R}}}$
,
${{{S}}^{{R}}}$
,
![]() ${{R}\to {S}}$
and
${{R}\to {S}}$
and
![]() ${{S}\leftarrow {R}}$
interchangeably, depending on how convenient they are. (E.g. we avoid
${{S}\leftarrow {R}}$
interchangeably, depending on how convenient they are. (E.g. we avoid
![]() ${{({{S}}^{{R}})}^{{Q}}}$
and write
${{({{S}}^{{R}})}^{{Q}}}$
and write
![]() ${{Q}\to {{S}}^{\textit{R}}}$
^R instead.)
${{Q}\to {{S}}^{\textit{R}}}$
^R instead.)
For instance, the
![]() ${{Used}\to (\leq )}$
higher-order relation relates attributes
${{Used}\to (\leq )}$
higher-order relation relates attributes
![]() ${{date}}$
and
${{date}}$
and
![]() ${{expiry}}$
in (4.2), expressing the semantic constraint that the use of a coupon can only occur on a date prior (
${{expiry}}$
in (4.2), expressing the semantic constraint that the use of a coupon can only occur on a date prior (
![]() ${\leq }$
) to its expiry date.
${\leq }$
) to its expiry date.
Reynolds arrows are central to the inference of free theorems, as will be shown later, in particular in the following situation, in which
![]() ${{R}}$
is the converse of a function (
${{R}}$
is the converse of a function (
![]() ${R}\mathbin{:=}{{h}}^\circ$
) and
${R}\mathbin{:=}{{h}}^\circ$
) and
![]() ${{S}}$
is a function (
${{S}}$
is a function (
![]() ${{S}\mathbin{:=}{k}}$
):
${{S}\mathbin{:=}{k}}$
):

By shunting
![]() ${{{h}}}^\circ$
in (4.6) via (3.4),
${{{h}}}^\circ$
in (4.6) via (3.4),
![]() ${{{h}}^\circ\to {k}}$
becomes the higher-order function
${{{h}}^\circ\to {k}}$
becomes the higher-order function
as can be easily checked:

The special cases of (4.7),
(for A=B) and
(for
![]() ${{C}\mathrel{=}{D}}$
) capture post-and pre-composition, that is:
${{C}\mathrel{=}{D}}$
) capture post-and pre-composition, that is:
By taking converses of both sides of (4.5) and swapping
![]() ${{f}}$
and
${{f}}$
and
![]() ${{g}}$
via shunting rules (3.3, 3.4), one gets
${{g}}$
via shunting rules (3.3, 3.4), one gets
Thus:
Higher-order Reynolds squares Exponential relations
![]() ${{{S}}^{{R}}}$
can involve other exponentials, for instance
${{{S}}^{{R}}}$
can involve other exponentials, for instance
![]() ${{({{S}}^{{Q}})}^{{R}}}$
i.e.
${{({{S}}^{{Q}})}^{{R}}}$
i.e.
![]() ${{R}\to {{S}}^Q}$
. This happens frequently with functional programmers, who tend to use functions curried rather than uncurried. Such is the case in
${{R}\to {{S}}^Q}$
. This happens frequently with functional programmers, who tend to use functions curried rather than uncurried. Such is the case in

Let us unfold this, assuming all fresh variables universally quantified:

Perfect squares Allelations in square (4.6) but the pre-producer are functions. Suppose now that all relations are functions in a magic square (2.1). Then, by (3.5) path comparison becomes path equality and producer/consumer paths become interchangeable. In this case, we drop the
![]() ${ \subseteq }$
symbol from the square:
${ \subseteq }$
symbol from the square:

Clearly:
5 More on Reynolds square expressiveness
Let the pre-producer
![]() ${{R}}$
of a Reynolds square (4.1) be the identity:
${{R}}$
of a Reynolds square (4.1) be the identity:

In this case,
![]() ${{f}}$
and
${{f}}$
and
![]() ${{g}}$
have the same input type and are said to be pointwise
${{g}}$
have the same input type and are said to be pointwise
![]() ${{S}}$
-related. Using the dotted notation
${{S}}$
-related. Using the dotted notation
![]() ${\stackrel.{{S}}}$
for
${\stackrel.{{S}}}$
for
![]() ${{{S}}^{{id}}}$
, one may write
${{{S}}^{{id}}}$
, one may write
![]() ${{f}\;\stackrel.{{S}}\;{g}}$
to mean square (5.1), that is:
${{f}\;\stackrel.{{S}}\;{g}}$
to mean square (5.1), that is: ![]() . Thus, the following (useful) “lifting” rule:
. Thus, the following (useful) “lifting” rule:
A typical situation arises in (5.1) when the post-consumer
![]() ${{S}}$
is an ordering
${{S}}$
is an ordering
![]() ${(\leq )}$
.
${(\leq )}$
.
Then
![]() ${{f}\;\stackrel.{\leq }\;{g}}$
(i.e.
${{f}\;\stackrel.{\leq }\;{g}}$
(i.e.
![]() ${{{f}}\subseteq{(\leq ) \cdot {g}}}$
) means that
${{{f}}\subseteq{(\leq ) \cdot {g}}}$
) means that
![]() ${{f}\;{a}\leq {g}\;{a}}$
for every input
${{f}\;{a}\leq {g}\;{a}}$
for every input
![]() ${{a}}$
, i.e.
${{a}}$
, i.e.
![]() ${{f}}$
is pointwise-smaller than
${{f}}$
is pointwise-smaller than
![]() ${{g}}$
with respect to
${{g}}$
with respect to
![]() ${(\leq )}$
.
${(\leq )}$
.
Relational types. The intersection of
![]() ${{{S}}^{{R}}}$
and (higher-order) id captures all Reynolds squares (4.1) in which
${{{S}}^{{R}}}$
and (higher-order) id captures all Reynolds squares (4.1) in which
![]() ${{f}\mathrel{=}{g}}$
:
${{f}\mathrel{=}{g}}$
:

In this case, we often abbreviate
![]() ${{f}\;({R}\to {S})\;{f}}$
to
${{f}\;({R}\to {S})\;{f}}$
to
![]() ${{f}\mathbin{:}{R}\to {S}}$
, meaning that
${{f}\mathbin{:}{R}\to {S}}$
, meaning that
![]() ${{f}}$
has relational type
${{f}}$
has relational type
![]() ${{R}\to {S}}$
.Footnote
7
As seen before, this means that
${{R}\to {S}}$
.Footnote
7
As seen before, this means that
![]() ${{f}}$
maps
${{f}}$
maps
![]() ${{R}}$
-related inputs to
${{R}}$
-related inputs to
![]() ${{S}}$
-related outputs.
${{S}}$
-related outputs.
We can also write ![]() to express (5.3), stressing the fact that
to express (5.3), stressing the fact that
![]() ${{f}}$
can be regarded as a morphism of a category in which relations are the objects, mapped by functions that preserve them in the sense of (5.3). Indeed, by vertical composition (2.4) such morphisms compose and composition has identities (2.5).Footnote
8
${{f}}$
can be regarded as a morphism of a category in which relations are the objects, mapped by functions that preserve them in the sense of (5.3). Indeed, by vertical composition (2.4) such morphisms compose and composition has identities (2.5).Footnote
8
For
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
instantiated to preorders, say
${{S}}$
instantiated to preorders, say
![]() ${{R},{S}\mathbin{:=}(\sqsubseteq ),(\leq )}$
, the square
${{R},{S}\mathbin{:=}(\sqsubseteq ),(\leq )}$
, the square
![]() ${{f}\mathbin{:}(\sqsubseteq )\to (\leq )}$
is a concise way of saying that
${{f}\mathbin{:}(\sqsubseteq )\to (\leq )}$
is a concise way of saying that
![]() ${{f}}$
is a monotonic function:
${{f}}$
is a monotonic function: ![]() .
.
Predicates as types A special case of square (5.3) pops up wherever
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
are partial identities, also called coreflexive relations (
${{S}}$
are partial identities, also called coreflexive relations (
![]() ${{R}\; \subseteq \;{id}}$
and
${{R}\; \subseteq \;{id}}$
and
![]() ${{S}\; \subseteq \;{id}}$
). These relations are one-to-one correspondent to predicates: given a predicate
${{S}\; \subseteq \;{id}}$
). These relations are one-to-one correspondent to predicates: given a predicate ![]() , its associated coreflexive is the relation
, its associated coreflexive is the relation
![]() ${{{p}}?\mathbin{:}{A}\to {A}}$
defined by
${{{p}}?\mathbin{:}{A}\to {A}}$
defined by
Let
![]() ${{f}}$
have relational type
${{f}}$
have relational type
![]() ${{{p}}?\to {{q}}?}$
, as shown next:
${{{p}}?\to {{q}}?}$
, as shown next:

It is easy to see that (5.4) converts to the pointwise ![]() , meaning that
, meaning that
![]() ${{p}}$
is a sufficient condition on the input of
${{p}}$
is a sufficient condition on the input of
![]() ${{f}}$
(pre-condition) for
${{f}}$
(pre-condition) for
![]() ${{q}}$
to hold on the output (post-condition). By a not so dangerous abuse of notation one might abbreviate
${{q}}$
to hold on the output (post-condition). By a not so dangerous abuse of notation one might abbreviate
![]() ${{f}\mathbin{:}{{p}}?\to {{q}}?}$
to
${{f}\mathbin{:}{{p}}?\to {{q}}?}$
to
![]() ${{f}\mathbin{:}{p}\to {q}}$
and regard predicates
${{f}\mathbin{:}{p}\to {q}}$
and regard predicates
![]() ${{p}}$
and
${{p}}$
and
![]() ${{q}}$
as types.Footnote
9
${{q}}$
as types.Footnote
9
Another perspective is to look at (5.4) as a Hoare-triple
![]() ${{p}\;\{\mskip1.5mu {f}\mskip1.5mu\}\;{q}}$
where
${{p}\;\{\mskip1.5mu {f}\mskip1.5mu\}\;{q}}$
where
![]() ${{f}}$
is a functional program that satisfies such pre/post conditions.Footnote
10
${{f}}$
is a functional program that satisfies such pre/post conditions.Footnote
10
Algebraic squares A quite interesting situation arises in a Reynolds square (4.1) when
![]() ${{f},{g}\mathbin{:=}\alpha ,\beta }$
, where
${{f},{g}\mathbin{:=}\alpha ,\beta }$
, where
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\beta }$
are algebras of a relator
${\beta }$
are algebras of a relator ![]() :Footnote
11
:Footnote
11

The pointwise equivalent of (5.5) is ![]() , for all
, for all
![]() ${{x}}$
and
${{x}}$
and
![]() ${{y}}$
. For
${{y}}$
. For
![]() ${\alpha \mathrel{=}\beta }$
and endo-relation
${\alpha \mathrel{=}\beta }$
and endo-relation
![]() ${{R}}$
,
${{R}}$
, ![]() says that
says that
![]() ${{R}}$
is compatible with algebra
${{R}}$
is compatible with algebra
![]() ${\alpha }$
. For
${\alpha }$
. For
![]() ${{R}}$
an equivalence relation, it further says that
${{R}}$
an equivalence relation, it further says that
![]() ${{R}}$
is a congruence relation with respect to
${{R}}$
is a congruence relation with respect to
![]() ${\alpha }$
.Footnote
12
In case
${\alpha }$
.Footnote
12
In case
![]() ${{R}}$
is a function, say
${{R}}$
is a function, say
![]() ${{R}\mathbin{:=}{h}}$
in (5.5), the square becomes perfect
${{R}\mathbin{:=}{h}}$
in (5.5), the square becomes perfect

meaning that
![]() ${{h}}$
is an
${{h}}$
is an ![]() -homomorphism (Bird & de Moor, Reference Bird and de Moor1997).
-homomorphism (Bird & de Moor, Reference Bird and de Moor1997).
Coalgebraic squares Let
![]() ${{f},{g}\mathbin{:=}\gamma ,\phi }$
in a Reynolds square, where
${{f},{g}\mathbin{:=}\gamma ,\phi }$
in a Reynolds square, where
![]() ${\gamma }$
and
${\gamma }$
and
![]() ${\phi }$
are
${\phi }$
are ![]() -coalgebras:
-coalgebras:

Then
![]() ${{R}}$
is said to be a bisimulation (Sangiorgi, Reference Sangiorgi2004) between the two coalgebras, meaning:
${{R}}$
is said to be a bisimulation (Sangiorgi, Reference Sangiorgi2004) between the two coalgebras, meaning:
In case
![]() ${{R}}$
is coreflexive, it is known as a coalgebraic invariant (Barbosa et al., Reference Barbosa, Oliveira and Silva2008). Squares (5.5) and (5.6) show that, in a sense, a bisimulation is a kind of co-logical-relation.
${{R}}$
is coreflexive, it is known as a coalgebraic invariant (Barbosa et al., Reference Barbosa, Oliveira and Silva2008). Squares (5.5) and (5.6) show that, in a sense, a bisimulation is a kind of co-logical-relation.
Galois connections. To complete this review of concepts that magic squares are able to easily capture, let
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
in (4.1) be two preorders,
${{S}}$
in (4.1) be two preorders,
![]() ${(\sqsubseteq )}$
and
${(\sqsubseteq )}$
and
![]() ${(\leq )}$
respectively. Moreover, reverse the direction of
${(\leq )}$
respectively. Moreover, reverse the direction of
![]() ${{f}}$
and let the square be perfect:
${{f}}$
and let the square be perfect:

This very special kind of square is known as a Galois connection (GC) between two so-called adjoint functions,
![]() ${{f}}$
(the lower or left adjoint) and
${{f}}$
(the lower or left adjoint) and
![]() ${{g}}$
(the upper or right adjoint). Going pointwise in (5.7) via (2.2, 3.2) etc one gets:
${{g}}$
(the upper or right adjoint). Going pointwise in (5.7) via (2.2, 3.2) etc one gets:
Two cancellation laws are easily obtained from (5.8):

These inequalities tell that f and g are inverses of each other in an imperfect way: the round-trip
![]() ${{f} \cdot {g}}$
loses information while
${{f} \cdot {g}}$
loses information while
![]() ${{g} \cdot {f}}$
yields an over-approximation of its input. This is captured by the diagram
${{g} \cdot {f}}$
yields an over-approximation of its input. This is captured by the diagram

and often abbreviated by simply writing
![]() ${{f}\mathbin\dashv {g}}$
.
${{f}\mathbin\dashv {g}}$
.
Examples of the usefulness of GCs in both mathematics and computing are abundant, see e.g. von Karger (Reference von Karger1998), Backhouse & Backhouse (Reference Backhouse and Backhouse2004), Mu & Oliveira (Reference Mu and Oliveira2011). The following GC between multiplication and whole division in the natural numbers
—
![]() ${( \times {y})\mathbin\dashv (\div {y})}$
in short, for
${( \times {y})\mathbin\dashv (\div {y})}$
in short, for
![]() ${{y}\not=\mathrm{0}}$
— will be of interest in the sequel.
${{y}\not=\mathrm{0}}$
— will be of interest in the sequel.
6 Free theorem squares
In his landmark paper Theorems for free!, Philip Wadler (Reference Wadler1989) wrote: “From the type of a polymorphic function we can derive a theorem that it satisfies. (…) How useful are the theorems so generated? Only time and experience will tell (…)”. Under this “theorems for free” catchy phrase, Wadler made popular an important result on parametric polymorphism due to John Reynolds (Reference Reynolds1983). Four decades later there is ample evidence that such free theorems are indeed very useful, see for instance the work by Backhouse & Backhouse (Reference Backhouse and Backhouse2004), Voigtländer (Reference Voigtländer, Shao and Pierce2009) and Hackett & Hutton (Reference Hackett and Hutton2015).
The rest of this paper will be devoted to one particular application of such free theorems. Before that, the question arises: what is a free theorem and how does one derive it (for free)? It turns out that free theorems are magic squares. To put it simply, let a parametric function ![]() be given. Then its free theorem states that
be given. Then its free theorem states that
![]() ${{f}}$
has relational type
${{f}}$
has relational type
for any
![]() ${{R}}$
relating its parameters, as shown in the corresponding square:
${{R}}$
relating its parameters, as shown in the corresponding square:

This extends to multiparametric functions, as shown next with a simple example: consider the Haskell constant function
![]() ${\mathsf{const}\mathbin{:}{a}\to {b}\to {a}}$
. In exponential notation (and following our uppercase notation for type parameters), we may write
${\mathsf{const}\mathbin{:}{a}\to {b}\to {a}}$
. In exponential notation (and following our uppercase notation for type parameters), we may write
![]() ${\mathsf{const}\mathbin{:}{A}\to {{A}}^{{B}}}$
. Then, by (6.1),
${\mathsf{const}\mathbin{:}{A}\to {{A}}^{{B}}}$
. Then, by (6.1),
![]() ${\mathsf{const}}$
has relational type
${\mathsf{const}}$
has relational type
![]() ${{R}\to {{R}}^{\textit{S}}}$
, that is,
${{R}\to {{R}}^{\textit{S}}}$
, that is,
holds, cf.

As already mentioned, this square is the free theorem of
![]() ${\mathsf{const}}$
. Recalling (4.15, 4.16), its pointwise version is, for all
${\mathsf{const}}$
. Recalling (4.15, 4.16), its pointwise version is, for all
![]() ${{a}}$
,
${{a}}$
,
![]() ${{b}}$
,
${{b}}$
,
![]() ${{c}}$
,
${{c}}$
,
![]() ${{d}}$
:
${{d}}$
:
As a foretaste of what is to come, let us see how productive (6.2) is. Select, for instance,
![]() ${{R},{S}\mathbin{:=}{id},{k}}$
. Then (6.2) becomes
${{R},{S}\mathbin{:=}{id},{k}}$
. Then (6.2) becomes
![]() ${\mathsf{const}\; \subseteq \;{{id}}^{{k}} \cdot \mathsf{const}}$
that, by (4.13,3.3) and (3.5) becomes
${\mathsf{const}\; \subseteq \;{{id}}^{{k}} \cdot \mathsf{const}}$
that, by (4.13,3.3) and (3.5) becomes
![]() ${( \cdot {k}) \cdot \mathsf{const}\mathrel{=}\mathsf{const}}$
, which is equivalent to
${( \cdot {k}) \cdot \mathsf{const}\mathrel{=}\mathsf{const}}$
, which is equivalent to
![]() ${\mathsf{const}\;{a} \cdot {k}\mathrel{=}\mathsf{const}\;{a}}$
— a well-known fusion law for constant functions. Swapping the roles of
${\mathsf{const}\;{a} \cdot {k}\mathrel{=}\mathsf{const}\;{a}}$
— a well-known fusion law for constant functions. Swapping the roles of
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
to
${{S}}$
to
![]() ${{R},{S}\mathbin{:=}{k},{id}}$
, one gets
${{R},{S}\mathbin{:=}{k},{id}}$
, one gets
![]() ${\mathsf{const} \cdot {k}\; \subseteq \;{{k}}^{{id}} \cdot \mathsf{const}}$
which, by (4.8) etc, rewrites to
${\mathsf{const} \cdot {k}\; \subseteq \;{{k}}^{{id}} \cdot \mathsf{const}}$
which, by (4.8) etc, rewrites to
![]() ${\mathsf{const} \cdot {k}\mathrel{=}({k} \cdot ) \cdot \mathsf{const}}$
yielding another well-known law:
${\mathsf{const} \cdot {k}\mathrel{=}({k} \cdot ) \cdot \mathsf{const}}$
yielding another well-known law:
![]() ${{k} \cdot \mathsf{const}\;{a}\mathrel{=}\mathsf{const}\;({k}\;{a})}$
.
${{k} \cdot \mathsf{const}\;{a}\mathrel{=}\mathsf{const}\;({k}\;{a})}$
.
Flipping. As another example, consider the well-known function in Haskell that swaps the arguments of a curried function:
Its free theorem states that ![]() has relational type
has relational type
![]() ${{{{Q}}^{{S}}}^{{R}}\to {{{Q}}^{{R}}}^{{S}}}$
meaning
${{{{Q}}^{{S}}}^{{R}}\to {{{Q}}^{{R}}}^{{S}}}$
meaning
that is,

where (as in the sequel) we use the tilde notation ![]() to abbreviate
to abbreviate ![]() , as in the right hand square above. For
, as in the right hand square above. For
![]() ${{Q}\mathbin{:=}{id},{S}\mathbin{:=}{id}\;{and}\;{R}\mathbin{:=}{r}}$
(a function), one gets:
${{Q}\mathbin{:=}{id},{S}\mathbin{:=}{id}\;{and}\;{R}\mathbin{:=}{r}}$
(a function), one gets:

This is known as the fusion-law of flipping (Oliveira, Reference Oliveira2020).
Flipping will be relevant in the rest of the paper, in which we shall investigate the theory that stems from the free theorems of two very popular functional programming combinators,
![]() ${\mathsf{foldl}{}{}}$
and
${\mathsf{foldl}{}{}}$
and
![]() ${\mathsf{foldr}{}{}}$
, heading toward discussing under what conditions they have the same behaviour.
${\mathsf{foldr}{}{}}$
, heading toward discussing under what conditions they have the same behaviour.
7 foldl and foldr
In Haskell, there is a class
![]() ${{Foldable}}$
that, according to the standard documentation, “represents data structures that can be reduced to a summary value one element at a time”.Footnote
13
The class offers, in particular, two standard ways of accessing foldable data structures:
${{Foldable}}$
that, according to the standard documentation, “represents data structures that can be reduced to a summary value one element at a time”.Footnote
13
The class offers, in particular, two standard ways of accessing foldable data structures:
Lists are a prominent instance of the class — and, indeed, its main inspiration — whose standard definitions are:

The free theorems of
![]() ${\mathsf{foldl}{}{}}$
and
${\mathsf{foldl}{}{}}$
and
![]() ${\mathsf{foldr}{}{}}$
— valid for any instance
${\mathsf{foldr}{}{}}$
— valid for any instance ![]() of class
of class
![]() ${{Foldable}}$
— can be written in the form of relational types:Footnote
14
${{Foldable}}$
— can be written in the form of relational types:Footnote
14
There are two squares involved in each type. The one on the left will play the role of a side-condition for the one on the right to hold.
Foldl. Let us see (7.2) first:

For
![]() ${{R},{S}\mathbin{:=}{id},{h}}$
(hence
${{R},{S}\mathbin{:=}{id},{h}}$
(hence
![]() ${{A}\mathbin{:=}{X}}$
), both
${{A}\mathbin{:=}{X}}$
), both ![]() and
and
![]() ${{{S}}^{{R}}}$
reduce to
${{{S}}^{{R}}}$
reduce to
![]() ${({h} \cdot )}$
by
${({h} \cdot )}$
by ![]() Footnote
15
and (4.8). So the squares become perfect and one has:
Footnote
15
and (4.8). So the squares become perfect and one has:

Going pointwise via the usual laws, from (7.5) one gets:
This is the fusion law of
![]() ${\mathsf{foldl}{}{}}$
given by Bird & Gibbons (Reference Bird and Gibbons2020), who prove it (for lists) by finite-list induction. Note however that, as a corollary of a free theorem, it needs no dedicated proof and it holds for all instances of class
${\mathsf{foldl}{}{}}$
given by Bird & Gibbons (Reference Bird and Gibbons2020), who prove it (for lists) by finite-list induction. Note however that, as a corollary of a free theorem, it needs no dedicated proof and it holds for all instances of class
![]() ${{Foldable}}$
, not just for lists. Moreover, the scope of (7.4) is far wider than perfect squares involving only functions, as shown next.
${{Foldable}}$
, not just for lists. Moreover, the scope of (7.4) is far wider than perfect squares involving only functions, as shown next.
To give a simple example, let
![]() ${{S}}$
be an ordering
${{S}}$
be an ordering
![]() ${(\leq )}$
and keep
${(\leq )}$
and keep
![]() ${{R}\mathbin{:=}{id}}$
. Since
${{R}\mathbin{:=}{id}}$
. Since ![]() both squares will feature the relational type
both squares will feature the relational type
![]() ${(\leq )\to {(\leq )}^{{id}}}$
. Then, if the left square holds, i.e. for all
${(\leq )\to {(\leq )}^{{id}}}$
. Then, if the left square holds, i.e. for all
![]() ${{b}}$
,
${{b}}$
,
![]() ${{y}}$
${{y}}$
then the right square
will hold too.
Perhaps more interesting is to observe that, if types a and b are replaced by predicates p and q, under the interpretation given by (5.4), then
is a corollary of the free theorem, saying:
NB:
![]() ${\mathsf{all}\;{p}}$
, available for all instances of class
${\mathsf{all}\;{p}}$
, available for all instances of class
![]() ${{Foldable}}$
, is the predicate associated to the coreflexive
${{Foldable}}$
, is the predicate associated to the coreflexive ![]() that relates a
that relates a ![]() -structure to itself if and only if all data in it satisfy predicate
-structure to itself if and only if all data in it satisfy predicate
![]() ${{p}}$
.
${{p}}$
.
Foldr. Repeating the above exercise for (7.3), on the right we get the same square as in (7.4), but the side condition on the left is different:

For
![]() ${{R},{S}\mathbin{:=}{id},{h}}$
, such a side-condition square unfolds to:
${{R},{S}\mathbin{:=}{id},{h}}$
, such a side-condition square unfolds to:

Altogether, one gets:
Going fully pointwise,
one obtains the fusion law of
![]() ${\mathsf{foldr}{}{}}$
proved for finite lists (by induction) by Bird & Gibbons (Reference Bird and Gibbons2020). Again we stress that (7.7) is a corollary of a free theorem and needs no proof, holding for all instances of class
${\mathsf{foldr}{}{}}$
proved for finite lists (by induction) by Bird & Gibbons (Reference Bird and Gibbons2020). Again we stress that (7.7) is a corollary of a free theorem and needs no proof, holding for all instances of class
![]() ${{Foldable}}$
.
${{Foldable}}$
.
Furthermore, by swapping the roles of
![]() ${{R}}$
and
${{R}}$
and
![]() ${{S}}$
and making
${{S}}$
and making
![]() ${{S},{R}\mathbin{:=}{id},{h}}$
, the side-condition square of (7.6) becomes
${{S},{R}\mathbin{:=}{id},{h}}$
, the side-condition square of (7.6) becomes
![]() ${{g}\;({{id}}^{{h}})\;{f}}$
which, by (4.17) is
${{g}\;({{id}}^{{h}})\;{f}}$
which, by (4.17) is
![]() ${{f}\mathrel{=}{g} \cdot {h}}$
. Replacing
${{f}\mathrel{=}{g} \cdot {h}}$
. Replacing
![]() ${{f}}$
in the right square we get
${{f}}$
in the right square we get

Law (7.9) is often referred to as the absorption law of “fmap” (![]() ) by
) by
![]() ${\mathsf{foldr}{}{}}$
. It is another corollary of free theorem (7.6) and therefore none of its instances in the
${\mathsf{foldr}{}{}}$
. It is another corollary of free theorem (7.6) and therefore none of its instances in the
![]() ${{Foldable}}$
class needs a proof. The default implementation of
${{Foldable}}$
class needs a proof. The default implementation of
![]() ${{foldMap}}$
in Data.Foldable arises from (7.9).
${{foldMap}}$
in Data.Foldable arises from (7.9).
Maybe Just to give an example of (7.8) holding for instances of class
![]() ${{Foldable}}$
other than lists, let us check the
${{Foldable}}$
other than lists, let us check the
![]() ${{Maybe}}$
instance defined in
${{Maybe}}$
instance defined in
![]() ${{{Data}.Foldable}}$
, with respect to (7.7):
${{{Data}.Foldable}}$
, with respect to (7.7):

We have two cases: for
![]() ${{xs}\mathbin{:=}\mathsf{Nothing}}$
, the right square trivially reduces to
${{xs}\mathbin{:=}\mathsf{Nothing}}$
, the right square trivially reduces to
![]() ${{h}\;{e}\mathrel{=}{h}\;{e}}$
and we are done. In the case
${{h}\;{e}\mathrel{=}{h}\;{e}}$
and we are done. In the case
![]() ${{xs}\mathbin{:=}\mathsf{Just}\;{x}}$
, we have
${{xs}\mathbin{:=}\mathsf{Just}\;{x}}$
, we have
![]() ${\mathsf{foldr}{{f}}{{e}}}$
${\mathsf{foldr}{{f}}{{e}}}$
![]() ${(\mathsf{Just}\;{x})} = {{f}\;{x}\;{e}}$
in (7.8) and
${(\mathsf{Just}\;{x})} = {{f}\;{x}\;{e}}$
in (7.8) and
![]() ${\mathsf{foldr}{{g}}{({h}\;{e})}\;(\mathsf{Just}\;{x})\mathrel{=}{g}\;{x}\;({h}\;{e})}$
. Then:
${\mathsf{foldr}{{g}}{({h}\;{e})}\;(\mathsf{Just}\;{x})\mathrel{=}{g}\;{x}\;({h}\;{e})}$
. Then:
![]() ${{g}\;{x}\;({h}\;{y})\mathrel{=}{h}\;({f}\;{x}\;{y})}$
${{g}\;{x}\;({h}\;{y})\mathrel{=}{h}\;({f}\;{x}\;{y})}$
![]() ${\Rightarrow }$
${\Rightarrow }$
![]() ${{h}\;({f}\;{x}\;{e})\mathrel{=}{g}\;{x}\;({h}\;{e})}$
trivially holds too.
${{h}\;({f}\;{x}\;{e})\mathrel{=}{g}\;{x}\;({h}\;{e})}$
trivially holds too.
Permutativity Let
![]() ${{f}}$
and g be the same function in (7.7), say s, and
${{f}}$
and g be the same function in (7.7), say s, and
![]() ${{h}\mathbin{:=}{s}\;{a}}$
:
${{h}\mathbin{:=}{s}\;{a}}$
:
Property
![]() ${({s}\;{x}) \cdot ({s}\;{a})\mathrel{=}({s}\;{a}) \cdot ({s}\;{x})}$
— i.e. the fully pointwise
${({s}\;{x}) \cdot ({s}\;{a})\mathrel{=}({s}\;{a}) \cdot ({s}\;{x})}$
— i.e. the fully pointwise
![]() ${{s}\;{x}\;({s}\;{a}\;{y})\mathrel{=}{s}\;{a}\;({s}\;{x}\;{y})}$
— is called (left) permutativity by Danvy (Reference Danvy2023).Footnote
16
It can be easily shown that if s is associative and commutative then it is permutative:
${{s}\;{x}\;({s}\;{a}\;{y})\mathrel{=}{s}\;{a}\;({s}\;{x}\;{y})}$
— is called (left) permutativity by Danvy (Reference Danvy2023).Footnote
16
It can be easily shown that if s is associative and commutative then it is permutative:

That is:
On the other hand, if s is permutative and has unit e, then s is commutative:
![]() ${{s}\;{x}\;({s}\;{a}\;{e})\mathrel{=}{s}\;{a}\;({s}\;{x}\;{e})}$
and thus
${{s}\;{x}\;({s}\;{a}\;{e})\mathrel{=}{s}\;{a}\;({s}\;{x}\;{e})}$
and thus
![]() ${{s}\;{x}\;{a}\mathrel{=}{s}\;{a}\;{x}}$
.
${{s}\;{x}\;{a}\mathrel{=}{s}\;{a}\;{x}}$
.
8 Universal properties
Suppose a particular instance ![]() of
of
![]() ${{Foldable}}$
such that
${{Foldable}}$
such that
holds, for some
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\gamma }$
. By (7.6) the types are
${\gamma }$
. By (7.6) the types are ![]() and
and ![]() . That is,
. That is,
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\gamma }$
are constructors of type
${\gamma }$
are constructors of type ![]() . Such is the case of lists, in which
. Such is the case of lists, in which
![]() ${\mathsf{foldr}{(\mathbin{:})}{[\mskip1.5mu \mskip1.5mu]}\mathrel{=}{id}}$
, that is,
${\mathsf{foldr}{(\mathbin{:})}{[\mskip1.5mu \mskip1.5mu]}\mathrel{=}{id}}$
, that is,
![]() ${\alpha \mathrel{=}(\mathbin{:})}$
and
${\alpha \mathrel{=}(\mathbin{:})}$
and
![]() ${\gamma \mathrel{=}[\mskip1.5mu \mskip1.5mu]}$
in (8.1). Then one has the following corollary of (7.8):
${\gamma \mathrel{=}[\mskip1.5mu \mskip1.5mu]}$
in (8.1). Then one has the following corollary of (7.8):
which, by introducing
![]() ${{z}\mathrel{=}{h}\;\gamma }$
and dropping
${{z}\mathrel{=}{h}\;\gamma }$
and dropping
![]() ${{xs}}$
, becomes:
${{xs}}$
, becomes:
Thiseans that, if
![]() ${\gamma }$
and
${\gamma }$
and
![]() ${\alpha }$
exist such that (8.1) holds, by the free-theorem of
${\alpha }$
exist such that (8.1) holds, by the free-theorem of
![]() ${\mathsf{foldr}{}{}}$
the system of equations (in
${\mathsf{foldr}{}{}}$
the system of equations (in
![]() ${{h}}$
)
${{h}}$
)

has a unique solution,
![]() ${{h}\mathrel{=}\mathsf{foldr}{{g}}{{z}}}$
. Since
${{h}\mathrel{=}\mathsf{foldr}{{g}}{{z}}}$
. Since
![]() ${\mathsf{foldr}{{g}}{{z}}}$
satisfies the equations for which it is a solution, then
${\mathsf{foldr}{{g}}{{z}}}$
satisfies the equations for which it is a solution, then
hold, unveiling the definition of
![]() ${\mathsf{foldr}{}{}}$
itself. Moreover, this definition is mathematically equivalent to (just replace h by
${\mathsf{foldr}{}{}}$
itself. Moreover, this definition is mathematically equivalent to (just replace h by
![]() ${\mathsf{foldr}{{g}}{{z}}}$
and simplify):
${\mathsf{foldr}{{g}}{{z}}}$
and simplify):
Putting (8.2,8.4) together, we get the universal property of
![]() ${\mathsf{foldr}{}{}}$
,
${\mathsf{foldr}{}{}}$
,
which, for lists, is
cf. e.g. Hutton (Reference Hutton1999).
9 Is foldl equal to foldr?
Looking at (7.1), the type-wise distance between
![]() ${\mathsf{foldr}{}{}}$
and
${\mathsf{foldr}{}{}}$
and
![]() ${\mathsf{foldl}{}{}}$
is the flip (6.3) of the first parameter.Footnote
17
So the “best fit” one can aim at here is
${\mathsf{foldl}{}{}}$
is the flip (6.3) of the first parameter.Footnote
17
So the “best fit” one can aim at here is
possibly valid for (as wide as possible) a class of functions f and instances of class
![]() ${{Foldable}}$
.
${{Foldable}}$
.
Our first step is to conjecture a definition for
![]() ${\mathsf{foldl}{}{}}$
that is type-wise consistent (over the
${\mathsf{foldl}{}{}}$
that is type-wise consistent (over the
![]() ${{Foldable}}$
class) with (8.3) which — recall — was derived from the free-theorem of
${{Foldable}}$
class) with (8.3) which — recall — was derived from the free-theorem of
![]() ${\mathsf{foldr}{}{}}$
. A possibility is to involve
${\mathsf{foldr}{}{}}$
. A possibility is to involve
![]() ${\mathsf{foldr}{}{}}$
itself in the definition. Looking at the flipped
${\mathsf{foldr}{}{}}$
itself in the definition. Looking at the flipped
![]() ${{f}}$
in (9.1), which is of type
${{f}}$
in (9.1), which is of type
![]() ${{A}\to {{B}}^{\textit{B}}}$
, one can think of expressing
${{A}\to {{B}}^{\textit{B}}}$
, one can think of expressing ![]() by a higher-order fold:
by a higher-order fold:

Note the type
![]() ${\theta\;{f}\mathbin{:}{A}\to {({{B}}^{{B}})}^{({{B}}^{{B}})}}$
for
${\theta\;{f}\mathbin{:}{A}\to {({{B}}^{{B}})}^{({{B}}^{{B}})}}$
for
![]() ${{f}\mathbin{:}{B}\to {{B}}^{{A}}}$
.
${{f}\mathbin{:}{B}\to {{B}}^{{A}}}$
.
Next, we unfold (9.2) via universal property (8.5). For easier reference, we instantiate (with no loss of generality)
![]() ${\gamma }$
and
${\gamma }$
and
![]() ${\alpha }$
for lists, as these are very well known to functional programmers:
${\alpha }$
for lists, as these are very well known to functional programmers:

This confirms the standard definition of
![]() ${\mathsf{foldl}{}{}}$
for lists.
${\mathsf{foldl}{}{}}$
for lists.
Universal-
![]() ${\mathsf{foldl}{}{}}$
An advantage of defining
${\mathsf{foldl}{}{}}$
An advantage of defining
![]() ${\mathsf{foldl}{}{}}$
“as a
${\mathsf{foldl}{}{}}$
“as a
![]() ${\mathsf{foldr}{}{}}$
” (9.2) is that the universal property of the latter induces the universal property of the former:Footnote
18
${\mathsf{foldr}{}{}}$
” (9.2) is that the universal property of the latter induces the universal property of the former:Footnote
18

Thus we get the universal-property of
![]() ${\mathsf{foldl}{}{}}$
:
${\mathsf{foldl}{}{}}$
:
Equating
![]() ${\mathsf{foldl}{}{}}$
and
${\mathsf{foldl}{}{}}$
and
![]() ${\mathsf{foldr}{}{}}$
Next we address the question (9.1) that opened this section: under what conditions does
${\mathsf{foldr}{}{}}$
Next we address the question (9.1) that opened this section: under what conditions does
![]() hold? We can use
hold? We can use
![]() ${\mathsf{foldl}{}{}}$
-universal (9.3) to find an answer:
${\mathsf{foldl}{}{}}$
-universal (9.3) to find an answer:

We conclude that ![]() holds for the instances of class
holds for the instances of class
![]() ${{Foldable}}$
such that (8.1) holds, provided that
${{Foldable}}$
such that (8.1) holds, provided that ![]() is a permutative operation (recall Section 7).
is a permutative operation (recall Section 7).
The usual assumption that
![]() ${\mathsf{foldl}{{f}}{{e}}}$
and
${\mathsf{foldl}{{f}}{{e}}}$
and ![]() are the same for
are the same for
![]() ${{f}}$
associative and
${{f}}$
associative and
![]() ${{e}}$
its unitFootnote
19
is therefore too strong. By (7.11) we know that associativity and commutativity ensure permutativity.Footnote
20
However, the converse implication does not hold, take e.g.
${{e}}$
its unitFootnote
19
is therefore too strong. By (7.11) we know that associativity and commutativity ensure permutativity.Footnote
20
However, the converse implication does not hold, take e.g.
![]() ${{f}\mathrel{=}(\div )}$
(5.9) as counter-example: neither
${{f}\mathrel{=}(\div )}$
(5.9) as counter-example: neither
![]() ${(\div }$
) nor
${(\div }$
) nor ![]() are associative or commutative, and yet
are associative or commutative, and yet ![]() is permutative. Why? Let us check it by indirect equality (Dijkstra, Reference Dijkstra2001):
is permutative. Why? Let us check it by indirect equality (Dijkstra, Reference Dijkstra2001):

Also to be noted, the second parameter e remains unconstrained in both folds. For example:

Of course, the previous calculation can generalize to any Galois connection
![]() ${{f}\mathbin\dashv {g}}$
.
${{f}\mathbin\dashv {g}}$
.
Altogether, we have that ![]() is granted for those g that, being neither associative nor commutative, participate in an adjunction
is granted for those g that, being neither associative nor commutative, participate in an adjunction
![]() ${{f}\mathbin\dashv {g}}$
whose other adjoint is so.
${{f}\mathbin\dashv {g}}$
whose other adjoint is so.
10 Summary and discussion
This article addresses the use of relational, pointfree techniques in reasoning about functional programs. In particular, it shows the role of relational semi-commutative squares (suggestively referred to as “magic” squares) in expressing (and reasoning about) formal concepts relevant to computing and, in particular, to FP. By switching to relational types one gets a quite rich setting in which programming and expressing properties of programs blend naturally.Footnote
21
The calculation of “theorems-for-free” is given as an application of this, in particular used to infer conditions for the combinators
![]() ${\mathsf{foldl}{{f}}{{e}}}$
and
${\mathsf{foldl}{{f}}{{e}}}$
and ![]() to compute the same output for any
to compute the same output for any
![]() ${{e}}$
.
${{e}}$
.
This research shares much with the work of Backhouse & Backhouse (Reference Backhouse and Backhouse2004), who give perhaps the most impressive account of the power of free-theorems of all literature on the subject, contributing with sharp results on the role of Galois connections in (higher-order) abstract interpretation. Such a paper is, however, not an easy read for the average functional programmer. The (less ambitious) approach proposed in the current paper bears in mind the need to make such fantastic results more and more accessible to the programming community.
There is a sharp contrast between the effectiveness of relational reasoning in the style of e.g. Bird & de Moor (Reference Bird and de Moor1997) and Backhouse & Backhouse (Reference Backhouse and Backhouse2004) and the low popularity of the methodology. This is rather unfortunate. Having decided to teach such relational methods to computer science students two decades ago, the author has invested into widening scope and applying such a reasoning style to areas such as database programming, formal modeling and, of course, functional programming (Oliveira, Reference Oliveira2024). In this process, diagrams have proved very effective as a device enhancing the perception of the information flow and of how the overall reasoning is conducted. Thus magic squares (MS) emerged as a simple, yet very powerful design unit of a pointfree, relational approach to formal reasoning.
Relational exponentiation
![]() ${{{S}}^{{R}}}$
plays a major role in the way higher-order functions are handled. By MS vertical composition (2.4), one immediately infers that, as expected, it is monotone on the base and anti-monotonic on the exponent:
${{{S}}^{{R}}}$
plays a major role in the way higher-order functions are handled. By MS vertical composition (2.4), one immediately infers that, as expected, it is monotone on the base and anti-monotonic on the exponent:

We also know that
![]() ${{{id}}^{{id}}\mathrel{=}{id}}$
(4.14). By horizontal composition (2.3), we get
${{{id}}^{{id}}\mathrel{=}{id}}$
(4.14). By horizontal composition (2.3), we get
However, the converse inclusion does not hold and so relational exponentiation is not in general a (bi)relator.Footnote 22 Backhouse & Backhouse (Reference Backhouse and Backhouse2004) give conditions for strengthening (10.1) to an equality that include the cases involving functions and converses of functions used in this paper.
Functional programmers have realized that many abstract concepts they love have a categorical nature. This has led to a strong focus on explaining the whole paradigm in categorial terms, see e.g. Hinze et al. (Reference Hinze, Wu and Gibbons2015) — a trend that of course includes the today so important concept of a monad (Wadler, Reference Wadler1990; Moggi, Reference Moggi1991; Gibbons & Hinze, Reference Gibbons and Hinze2011). It all happened as if, in a sense, FP eventually came to rescue category theory from being considered by the programming community as mere abstract nonsense, with no practical application. In this setting, theorems-for-free have been formalized via (lax) dinatural transformations (Hackett &Hutton, Reference Hackett and Hutton2015; Voigtländer, Reference Voigtländer2019) in order-enriched categories. We believe that the category of relations, which is “naturally” ordered by relation inclusion, provides an overall simpler approach, much in the spirit of the quote by Freyd & Scedrov (Reference Freyd and Scedrov1990) that opens this paper.
Framed in this trend, the
![]() ${\mathsf{foldl}{}{}\mathbin{/}\mathsf{foldr}{}{}}$
case study could have been given as a pointfree calculation carried out via the adjoint-fold theorem (Hinze, Reference Hinze2013; Oliveira, Reference Oliveira, Madeira and Martins2023) and enabled by the self-adjunction witnessed by
${\mathsf{foldl}{}{}\mathbin{/}\mathsf{foldr}{}{}}$
case study could have been given as a pointfree calculation carried out via the adjoint-fold theorem (Hinze, Reference Hinze2013; Oliveira, Reference Oliveira, Madeira and Martins2023) and enabled by the self-adjunction witnessed by
![]() ${{flip}}$
Footnote
23
— as in a similar calculation concerning left and right-iteration (Oliveira, Reference Oliveira2020). It should be noted that knowing that permutativity is enough for foldr/foldl “equality” is not new — see e.g. Danvy (Reference Danvy2023). Danvy’s reasoning is, however, quite different: he postulates permutativity as a side condition and then proves it in Coq by induction on lists. In this paper, permutativity arises by free-theorem calculation. Moreover, it shows that Danvy’s result can be extended via Galois connections.Footnote
24
${{flip}}$
Footnote
23
— as in a similar calculation concerning left and right-iteration (Oliveira, Reference Oliveira2020). It should be noted that knowing that permutativity is enough for foldr/foldl “equality” is not new — see e.g. Danvy (Reference Danvy2023). Danvy’s reasoning is, however, quite different: he postulates permutativity as a side condition and then proves it in Coq by induction on lists. In this paper, permutativity arises by free-theorem calculation. Moreover, it shows that Danvy’s result can be extended via Galois connections.Footnote
24
The generic approach to this case study given in the current paper throws attention to the
![]() ${{Foldable}}$
class of the Haskell standard library system. The permutativity of
${{Foldable}}$
class of the Haskell standard library system. The permutativity of
![]() ${{f}}$
that grants the
${{f}}$
that grants the ![]() outcome “for-free” is not alone: a reflection constraint (8.1) is also needed. This constraint is quite strong in the sense of identifying the type constructors
outcome “for-free” is not alone: a reflection constraint (8.1) is also needed. This constraint is quite strong in the sense of identifying the type constructors
![]() ${\gamma }$
and
${\gamma }$
and
![]() ${\alpha }$
of the particular
${\alpha }$
of the particular
![]() ${{Foldable}}$
instance in hands. The types of
${{Foldable}}$
instance in hands. The types of
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\gamma }$
in (8.1) clearly point to lists as being the prototypical instance of the class.
${\gamma }$
in (8.1) clearly point to lists as being the prototypical instance of the class.
It is not difficult to find instances of class
![]() ${{Foldable}}$
that do not meet reflection constraint (8.1) and for which the
${{Foldable}}$
that do not meet reflection constraint (8.1) and for which the
![]() ${\mathsf{foldl}{}{}\mathbin{/}\mathsf{foldr}{}{}}$
result cannot be obtained as in the current paper. Interestingly enough,
${\mathsf{foldl}{}{}\mathbin{/}\mathsf{foldr}{}{}}$
result cannot be obtained as in the current paper. Interestingly enough, ![]() seems to be granted across the class as an axiom, that is,
seems to be granted across the class as an axiom, that is, ![]() is the default definition of
is the default definition of
![]() ${\mathsf{foldl}{}{}}$
, assuming
${\mathsf{foldl}{}{}}$
, assuming
![]() ${\mathsf{foldr}{}{}}$
defined. Studying this better and applying the same kind of reasoning to other classes of the Haskell standard libraries is a topic for future research.
${\mathsf{foldr}{}{}}$
defined. Studying this better and applying the same kind of reasoning to other classes of the Haskell standard libraries is a topic for future research.
Acknowledgments
This work was supported by National Funds through the FCT – Fundação para a Ciência e a Tecnologia, I.P. (Portuguese Foundation for Science and Technology) within the IBEX project, with reference PTDC/CCI-COM/4280/2021.
Competing interests
The author reports no conflict of interest.


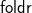
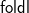



Discussions
No Discussions have been published for this article.