Article contents
Fair enumeration combinators
Published online by Cambridge University Press: 30 August 2017
Abstract
Enumerations represented as bijections between the natural numbers and elements of some given type have recently garnered interest in property-based testing because of their efficiency and flexibility. There are, however, many ways of defining these bijections, some of which are better than others. This paper offers a new property of enumeration combinators called fairness that identifies enumeration combinators that are better suited to property-based testing. Intuitively, the result of a fair combinator indexes into its argument enumerations equally when constructing its result. For example, extracting the nth element from our enumeration of three-tuples indexes about 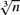 $\sqrt[3]{n}$ elements into each of its components instead of, say, indexing
$\sqrt[3]{n}$ elements into each of its components instead of, say, indexing 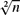 $\sqrt[2]{n}$ into one and
$\sqrt[2]{n}$ into one and 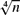 $\sqrt[4]{n}$ into the other two, as you would if a three-tuple were built out of nested pairs. Similarly, extracting the nth element from our enumeration of a three-way union returns an element that is
$\sqrt[4]{n}$ into the other two, as you would if a three-tuple were built out of nested pairs. Similarly, extracting the nth element from our enumeration of a three-way union returns an element that is  $\frac{n}{3}$ into one of the argument enumerators. The paper presents a semantics of enumeration combinators, a theory of fairness, proofs establishing fairness of our new combinators and that some combinations of fair combinators are not fair. We also report on an evaluation of fairness for the purpose of finding bugs in programming-language models. We show that fair enumeration combinators have complementary strengths to an existing, well-tuned ad hoc random generator (better on short time scales and worse on long time scales) and that using unfair combinators is worse across the board.
$\frac{n}{3}$ into one of the argument enumerators. The paper presents a semantics of enumeration combinators, a theory of fairness, proofs establishing fairness of our new combinators and that some combinations of fair combinators are not fair. We also report on an evaluation of fairness for the purpose of finding bugs in programming-language models. We show that fair enumeration combinators have complementary strengths to an existing, well-tuned ad hoc random generator (better on short time scales and worse on long time scales) and that using unfair combinators is worse across the board.
- Type
- Articles
- Information
- Copyright
- Copyright © Cambridge University Press 2017
References
- 7
- Cited by



Discussions
No Discussions have been published for this article.