Relatively strongly stratified turbulent flows tend to self-organise into a ‘layered anisotropic stratified turbulence’ (LAST) regime, characterised by relatively deep and well-mixed density ‘layers’ separated by relatively thin ‘interfaces’ of enhanced density gradient. Understanding the associated mixing dynamics is a central problem in geophysical fluid dynamics. It is challenging to study LAST mixing, as it is associated with Reynolds numbers 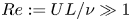$Re := UL/\nu \gg 1$ and Froude numbers 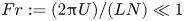$Fr :=(2{\rm \pi} U)/(L N) \ll 1$ (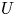$U$ and 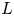$L$ being characteristic velocity and length scales, 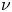$\nu$ the kinematic viscosity and 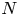$N$ the buoyancy frequency). Since a sufficiently large dynamic range (largely) unaffected by stratification and viscosity is required, it is also necessary for the buoyancy Reynolds number 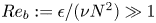$Re_{b} := \epsilon /(\nu N^{2}) \gg 1$, where 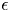$\epsilon$ is the (appropriately volume-averaged) turbulent kinetic energy dissipation rate. This requirement is exacerbated for oceanically relevant flows, as the Prandtl number 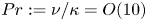$Pr := \nu /\kappa = {O}(10)$ in thermally stratified water (where 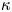$\kappa$ is the thermal diffusivity), thus leading (potentially) to even finer density field structures. We report here on four forced fully resolved direct numerical simulations of stratified turbulence at various Froude (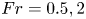$Fr=0.5, 2$) and Prandtl (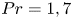$Pr=1, 7$) numbers forced so that 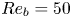$Re_{b}=50$, with resolutions up to 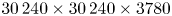$30\,240 \times 30\,240 \times 3780$. We find that, as 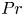$Pr$ increases, emergent ‘interfaces’ become finer and their contribution to bulk mixing characteristics decreases at the expense of the small-scale density structures populating the well-mixed ‘layers’. However, extreme mixing events (as quantified by significantly elevated local destruction rates of buoyancy variance 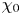$\chi _0$) are always preferentially found in the (statically stable) interfaces, irrespective of the value of 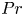$Pr$.

Amplification of velocity gradients, a key feature of turbulent flows, is affected by the non-local character of the incompressible fluid equations expressed by the second derivative (Hessian) of the pressure field. By analysing the structure of the flow in regions where the vorticity is the highest, we propose an approximate expression for the pressure Hessian in terms of the local vorticity, consistent with the existence of intense vortex tubes. Contrary to the often used simplification of an isotropic form for the pressure Hessian, which in effect inhibits vortex stretching, the proposed approximate form of the pressure Hessian enables much stronger vortex stretching. The prediction of the approximation proposed here is validated with results of direct numerical simulations of turbulent flows.

The squirmer is a popular model to analyse the fluid mechanics of a self-propelled object, such as a micro-organism. We demonstrate that some fore–aft symmetric squirmers can spontaneously self-propel above a critical Reynolds number. Specifically, we numerically study the effects of inertia on spherical squirmers characterised by an axially and fore–aft symmetric ‘quadrupolar’ distribution of surface-slip velocity; under creeping-flow conditions, such squirmers generate a pure stresslet flow, the stresslet sign classifying the squirmer as either a ‘pusher’ or ‘puller’. Assuming axial symmetry, and over the examined range of the Reynolds number $Re$ (defined based upon the magnitude of the quadrupolar squirming), we find that spontaneous symmetry breaking occurs in the puller case above $Re \approx 14.3$, with steady swimming emerging from that threshold consistently with a supercritical pitchfork bifurcation and with the swimming speed growing monotonically with $Re$.

Subcritical pipe flow transition has received a great deal of attention over the past decades, as it constitutes a quintessential bifurcation process between two metastable fluid states: the laminar and turbulent solutions. Coherent lower-branch structures, forming flow states that facilitate between these two attracting equilibria, have been proposed that together form an edge manifold in phase space separating relaminarizing from transitioning perturbations. Typically, direct numerical simulations or low-dimensional model equations have been used to study this edge manifold with bisection methods. In the article by Kaszás & Haller (J. Fluid Mech., vol. 979, 2024, A48), an effective nonlinear invariant-manifold technique has been applied to extract a low-dimensional, global representation of the phase-space dynamics directly from simulation data. It allows the computation of the intersection of the edge manifold with a low-dimensional surface that is strikingly accurate in predicting the long-term dynamics of perturbations about the lower-branch solution and thus provides an accessible parameterization of the edge manifold for subcritical pipe flow transition.

The synchronisation between rotating turbulent flows in periodic boxes is investigated numerically. The flows are coupled via a master–slave coupling, taking the Fourier modes with wavenumber below a given value $k_m$ as the master modes. It is found that synchronisation happens when $k_m$ exceeds a threshold value $k_c$, and $k_c$ depends strongly on the forcing scheme. In rotating Kolmogorov flows, $k_c\eta$ does not change with rotation in the range of rotation rates considered, $\eta$ being the Kolmogorov length scale. Even though the energy spectrum has a steeper slope, the value of $k_c\eta$ is the same as that found in isotropic turbulence. In flows driven by a forcing term maintaining constant energy injection rate, synchronisation becomes easier when rotation is stronger. Here, $k_c\eta$ decreases with rotation, and it is reduced significantly for strong rotations when the slope of the energy spectrum approaches $-3$. It is shown that the conditional Lyapunov exponent for a given $k_m$ is reduced by rotation in the flows driven by the second type of forcing, but it increases mildly with rotation for the Kolmogorov flows. The local conditional Lyapunov exponents fluctuate more strongly as rotation is increased, although synchronisation occurs as long as the average conditional Lyapunov exponents are negative. We also look for the relationship between $k_c$ and the energy spectra of the Lyapunov vectors. We find that the spectra always seem to peak at approximately $k_c$, and synchronisation fails when the energy spectra of the conditional Lyapunov vectors have a local maximum in the slaved modes.

The theory of transient growth describes how linear mechanisms can cause temporary amplification of disturbances even when the linearized system is asymptotically stable as defined by its eigenvalues. This growth is traditionally quantified by finding the initial disturbance that generates the maximum response at the peak time of its evolution. However, this can vastly overstate the growth of a real disturbance. In this paper, we introduce a statistical perspective on transient growth that models statistics of the energy amplification of the disturbances. We derive a formula for the mean energy amplification and spatial correlation of the growing disturbance in terms of the spatial correlation of the initial disturbance. The eigendecomposition of the correlation provides the most prevalent structures, which are the statistical analogue of the standard left singular vectors of the evolution operator. We also derive accurate confidence bounds on the growth by approximating the probability density function of the energy. Applying our analysis to Poiseuille flow yields a number of observations. First, the mean energy amplification is often drastically smaller than the maximum. In these cases, it is exceedingly unlikely to achieve near-optimal growth due to the exponential behaviour observed in the probability density function. Second, the characteristic length scale of the initial disturbances has a significant impact on the expected growth, with large-scale initial disturbances growing orders of magnitude more than small-scale ones. Finally, while the optimal growth scales quadratically with Reynolds number, the mean energy amplification scales only linearly for certain reasonable choices of the initial correlation.

The wake of two tandem square cylinders of identical width (d) is experimentally studied, with a view to understanding the dependence of the flow structure, aerodynamics forces and Strouhal number on the centre-to-centre spacing ratio L/d and Reynolds number Re, where L is the distance between the cylinder centres. Extensive measurements are carried out, using hot-wire, particle imaging velocimetry, laser-induced fluorescence flow visualization, surface-oil-flow visualization and surface pressure scanning techniques, for L/d = 1.0 ~ 5.0 and Re ≡ U∞d/ν = 2.8 × (103 ~ 104), where U∞ is the free-stream velocity and ν is the kinematic viscosity of the fluid. The flow is classified into four regimes, i.e. the extended-body (L/d ≤ 1.5–2.0), reattachment (1.5–2.0 < L/d < 2.7–3.2), co-shedding (L/d ≥ 3.0–3.4) and transition (2.7 ≤ L/d ≤ 3.3) where both reattachment and co-shedding phenomena may take place. The mean drag and fluctuating drag and lift exhibit distinct features for different flow regimes, which is fully consistent with the proposed flow classification. Comparison is made between this flow and the wake of two tandem circular cylinders, which provides valuable insight into the profound effect of the flow separation point and the presence of sharp corners on the flow development and classification.

We study numerically the microjetting mode obtained when a fluid is injected through a tube submerged in a uniaxial extensional flow. The steady solution to the full nonlinear Navier–Stokes equations is calculated. We obtain the linear global modes determining the linear stability of the steady solution. For sufficiently large outer viscosity, the flow remains stable for infinitely small values of the injected flow rate. This implies that jets with vanishing diameters can be produced regardless of the jet viscosity and outer flow strength. For a sufficiently small inner-to-outer viscosity ratio, the microjetting instability is associated only with the flow near the entrance of the jet. The tapering meniscus stretches and adopts a slender quasiconical shape. Consequently, the cone tip is exposed to an intense outer flow, which stabilizes the flow in the cone–jet transition region. This work presents the first evidence that fluid jets with arbitrarily small diameters can be stably produced via tip streaming. The results are related to those of a droplet in a uniaxial extensional flow with its equator pinned to an infinitely thin ring. The pinning of the equator drastically affects the droplet stability and breakup.

The axially symmetric deformation of a drop in a viscous fluid, under the influence of an externally imposed flow having simultaneous rotating and compressional or extensional components, is addressed. In the previous studies, two families of stationary drop shapes were constructed by simulating the dynamics of drop deformation: stable singly connected shapes with respect to axisymmetric disturbances, and unstable toroidal shapes. These two branches coexist at the same flow conditions, but were not connected. In this study, we obtain a new family of branches of unstable highly deformed stationary drops connecting with the stable flattened shapes and the toroidal ones. We use a method based on classical control theory. The controller is designed for a two-state dynamic model of the system and is employed on a high-order nonlinear dynamic model of the drop deformation. Through this feedback-control-centred approach, an extended collection of unstable stationary solutions is constructed, which spans the range from the loss of stability to the dimpled shapes almost collapsed at the centre. In the latter region, which was never obtained in previous studies, a multiplicity of solutions is identified.

The evaporation process in porous media typically experiences three main periods, among which the first period, named the constant rate period (CRP), performs most efficiently in removing liquid. We aim to prolong the CRP to very low degrees of saturation (S) and increase its evaporation rate by playing with heterogeneity in wettability and pore size. First, we show that a porous medium with a smaller contact angle at the surface and increasing contact angle towards the inside generally dries out faster compared with that with uniform contact angle. Second, a constant contact angle porous medium with smaller/larger pores in the surface/inside part dries out faster than a medium with uniform pore size. The underlying mechanism is the occurrence of a capillary pressure jump at the border between the two layers accompanied by enhanced capillary pumping, increasing/maintaining the interfacial area in the surface pores. Harnessing the potential of this mechanism, we propose an optimized strategy by combining two heterogeneity effects: increasing contact angle and pore size towards the inside. This strategy is found to be robust both for multilayer and larger systems. In this case, a small drying front first penetrates fast towards the inside and then expands, followed by a horizontal drying front moving back layer by layer to the surface. Quantitatively, compared with evaporation from a homogeneously porous medium with uniform contact angle where CRP stops at $S=0.64$, our optimized design can extend the CRP down to $S=0.12$, and decrease five-fold the drying time needed to reach $S=0.05$.

In this paper, we study wave scattering and radiation by a surface-piercing vertical truncated metamaterial cylinder composed of a closely spaced array of thin vertical barriers, between which fluid can flow. A theoretical model is developed under full depth-dependent linearised water wave theory, where an effective medium equation and effective boundary conditions are employed, respectively, to describe the fluid motion inside the cylinder and match the flow between the fluid regions in and outside the metamaterial cylinder. A damping mechanism is introduced at the surface of the fluid occupied by the metamaterial cylinder to consider the wave power dissipation in narrow gaps between the thin vertical plates. The wave excitation forces acting on the cylinder and the hydrodynamic coefficients can be calculated straightforwardly in terms of the velocity potential inside the cylinder. An alternative way is by using the velocity potential outside the cylinder, the expression of which has the reduction of the integral and an infinite accumulation that are included in the straightforward expression. The results highlight the patterns of the radiated waves induced by the oscillation of the cylinder and the characteristics of the hydrodynamic coefficients. The metamaterial cylinder when fixed in place and with a damping mechanism included is found to capture more wave power than that of a traditional axisymmetric heaving wave energy converter over a wide range of wave frequencies.

The development of simple, low-order and accurate unsteady aerodynamic models represents a crucial challenge for the design optimisation and control of fluid dynamical systems. In this work, wind tunnel experiments of a pitching NACA 0018 aerofoil conducted at a Reynolds number $Re = 2.8 \times 10^5$ and at different free-stream turbulence intensities are used to identify data-driven nonlinear state-space models relating the time-varying angle of attack of the aerofoil to the lift coefficient. The proposed state-space neural network (SS-NN) modelling technique explores an innovative methodology, which brings the flexibility of artificial neural networks into a classical state-space representation and offers new insights into the construction of reduced-order unsteady aerodynamic models. The work demonstrates that this technique provides accurate predictions of the nonlinear unsteady aerodynamic loads of a pitching aerofoil for a wide variety of angle-of-attack ranges and frequencies of oscillation. Results are compared with a modified version of the Goman–Khrabrov dynamic stall model. It is shown that the SS-NN methodology outperforms the classical semi-empirical dynamic stall models in terms of accuracy, while retaining a fast evaluation time. Additionally, the proposed models are robust to noisy measurements and do not require any pre-processing of the data, thus involving only a limited user interaction. Overall, these features make the SS-NN technique an excellent candidate for the construction of accurate data-driven models from experimental fluid dynamics data, and pave the way for their adoption in applications entailing design optimisation and real-time control of systems involving lift.

In order to improve the predictive abilities of weather and climate models, it is essential to understand the behaviour of wind stress at the ocean surface. Wind stress is contingent on small-scale interfacial dynamics typically not directly resolved in numerical models. Although skin friction contributes considerably to the total stress up to moderate wind speeds, it is notoriously challenging to measure and predict using physics-based approaches. This work proposes a supervised machine learning (ML) model that estimates the spatial distribution of the skin-friction drag over wind waves using solely wave elevation and wave age, which are relatively easy to acquire. The input–output pairs are high-resolution wave profiles and their corresponding surface viscous stresses collected from laboratory experiments. The ML model is built upon a convolutional neural network architecture that incorporates the Mish nonlinearity as its activation function. Results show that the model can accurately predict the overall distribution of viscous stresses; it captures the peak of viscous stress at/near the crest and its dramatic drop to almost null just past the crest in cases of intermittent airflow separation. The predicted area-aggregate skin friction is also in excellent agreement with the corresponding measurements. The proposed method offers a practical pathway for estimating both local and area-aggregate skin friction and can be easily integrated into existing numerical models for the study of air–sea interactions.

This paper investigates the effects of a light-actuated photosurfactant on the canonical problem of the linear stability of a viscous thread surrounded by a dynamically passive fluid. A model consisting of the Navier–Stokes equations and a set of molar concentration equations is presented that capture light-induced switching between two stable surfactant isomer states, trans and cis. These two states display significantly different interfacial properties, allowing for some external control of the stability behaviour of the thread via incident light. Normal modes are used to generate a generalized eigenvalue problem for the growth rate which is solved with a hybrid analytical and numerical method. The results are validated with appropriate analytical solutions of increasing complexity, beginning with a solution to a clean interface, then analytical solutions for one insoluble surfactant, one soluble surfactant and a special case of two photosurfactants with a spatially uniform undisturbed state. Presenting each of these cases allows for a holistic discussion of the effect of surfactants in general on the stability of a liquid thread. Finally, the numerical solutions in the presence of two photosurfactants that display radially non-uniform undisturbed states are presented, and details of the impact of the illumination on the linear stability of the thread are discussed.

Flow physics vary in different regimes across the full Mach number range, with our knowledge being particularly poor about the hypersonic regime. An Eulerian realization of the particles on demand method, a kinetic model formulated in the comoving reference frame, is proposed to simulate hypersonic compressible flows. The present model allows for flux evaluation in different reference frames, in this case rescaled and shifted by local macroscopic quantities, i.e. fluid speed and temperature. The resulting system of coupled hyperbolic equations is discretized in physical space with a finite volume scheme ensuring exact conservation properties. Regularization via Grad expansion is introduced to implement distribution function and flux transformation between different reference frames. It is shown that the proposed method possesses Galilean invariance at a Mach number up to $100$. Different benchmarks including both inviscid and viscous flows are reproduced with the Mach number up to $198$ and pressure ratio up to $10^5$. Finally, the new model is demonstrated to be capable of simulating hypersonic reactive flows, including one-dimensional and two-dimensional detonations. The developed methodology opens up possibilities for the simulation of the full range of compressible flows, without or with chemical reactions, from the subsonic to hypersonic regimes, leading to enhanced understanding of flow behaviours across the full Mach number range.

We investigate the linear instability of two-layer stratified shear flows in a sloping two-dimensional channel, subject to non-zero longitudinal gravitational forces. We reveal three previously unknown instabilities, distinct from the well-known Kelvin–Helmholtz instability and Holmboe wave instability, in that they have longer wavelengths (of the order of 10 to $10^3$ shear-layer depths) and often slower growth rates. Importantly, they can grow in background flows with gradient Richardson number $\gg 1$, which offers a new mechanism to sustain turbulence and mixing in strongly stratified flows. These instabilities are shown to be generic and relatively insensitive to Reynolds number, Prandtl number, base flow profile and boundary conditions. The nonlinear evolution of these instabilities is investigated through a forced direct numerical simulation, in which the background momentum and density are sustained. The growth of long unstable waves in background flows initially stable to short wave causes a decrease in the local gradient Richardson number. This leads to local nonlinear processes that result in small-scale overturns resembling Kelvin–Helmholtz billows. Our results establish a new energy exchange pathway, where the mean kinetic energy of a strongly stratified flow is extracted by primary unstable long waves and secondary short waves, and subsequently dissipated into internal energy.

We investigate the linear stability analysis of rotating electro-osmotic flow in confined and unconfined configurations by appealing to the Debye–Hückel approximation. Pertaining to flow in confined and unconfined domains, the stability equations are solved using the Galerkin method to obtain the stability picture. Both qualitative and quantitative aspects of Ekman spirals are examined in stable and unstable scenarios within the unconfined domain. Within the confined domain, the variation of the real growth rate and the transition to instability are analysed using the modified Routh–Hurwitz criteria, employed for the first time in this context. The stability of the underlying flow, characterized by the number of roots with a positive real part, is determined by establishing a Routhian table. The inferences of this analysis show that the velocity plane produces intriguing closed Ekman spirals, which diminish in size with an increase in the rotation speed $\omega$. The Ekman spirals in the stable region exhibit a distinct discontinuity, indicating the dissipation of disturbances over time. In the confined domain, the flow appears consistently stable for a set of involved parameters pertinent to this analysis, such as electrokinetic parameter $K=1.5$ and rotational parameter $\omega$ approximately up to $6$. However, the flow instabilities become evident for $K=1.5$ and $\omega \geq 6$.

The properties of multiphase flows are challenging to measure, and yet effective properties are fundamental to modelling and predicting flow behaviour. The current study is motivated by rheometric measurements of a gas-fluidized bed using a coaxial rheometer in which the fluidization rate and the rotational speed can be varied independently. The measured torque displays a range of rheological states: quasistatic, dense granular flow behaviour at low fluidization rates and low-to-moderate shear rates; turbulent toroidal-vortex flow at high shear rates and moderate-to-high fluidization rates; and viscous-like behaviour with rate-dependent torque at high shear rates and low fluidization or at low shear rates and high fluidization. To understand the solid-like to fluid-like transitions, additional experiments were performed in the same rheometer using single-phase liquid and liquid–solid suspensions. The fluidized bed experiments are modelled as a Bingham plastic for low fluidization rates, and as a shear-thinning Carreau liquid at high fluidization rates. The suspensions are modelled using the Krieger–Dougherty effective viscosity. The results demonstrate that, by using the effective properties, the inverse Bingham number marks the transition from solid-like to viscous-flow behaviour; a modified gap Reynolds number based on the thickness of the shear layer specifies the transition from solid-like to turbulent vortical flow; and a gap Reynolds number distinguishes viscous behaviour from turbulent vortical flow. The results further demonstrate that these different multiphase flows undergo analogous flow transitions at similar Bingham or Reynolds numbers and the corresponding dimensionless torques show comparable scaling in response to annular shear.

A spatially developing flat-plate boundary layer free from and two-way coupled with inertial solid particles is simulated to investigate the interaction between particles and the turbulent/non-turbulent interface. Particle Stokes numbers based on the outer scale are $St=2$ (low), 11 (moderate) and 53 (high). The Eulerian–Lagrangian point-particle approach is deployed for the simulation of particle-laden flow. The outer edge of the turbulent/non-turbulent interface layer is detected as an iso-surface of vorticity magnitude. Results show that the particles tend to accumulate below the interface due to the centrifugal effect of large-scale vortices in the outer region of wall turbulence and the combined barrier effect of potential flow. Consequently, the conditionally averaged fluid velocity and vorticity vary more significantly across the interface through momentum exchange and the feedback of force in the enstrophy transport. The large-scale structures in the outer layer of turbulence become smoother and less inclined in particle-laden flow due to the modulation of turbulence by the inertial particles. As a result, the geometric features of the interface layer are changed, namely, the spatial undulation increases, the fractal dimension decreases and the thickness becomes thinner in particle-laden flow as compared with unladen case. These effects become more pronounced as particle inertia increases.

An impulsively starting motion of two cylindrical bodies floating on a free liquid surface is considered. The shape of the cross-section of each body and the distance between them are arbitrary. The integral hodograph method is advanced to derive the complex velocity potential defined in a rectangular parameter region in terms of the elliptic quasi-doubly periodic Jacobi theta functions. A system of singular integral equations in the velocity magnitude on the free surface and in the slope of the wetted part of each body is derived using the kinematic boundary condition, which is then solved numerically. The velocity field, the pressure impulse on the bodies and the added mass coefficients of each body immediately after the impact are determined in a wide range of distances between the bodies and for cross-sectional shapes such as the flat plate and half-circle.