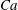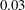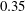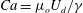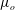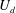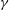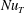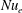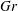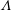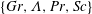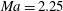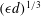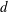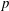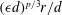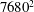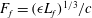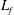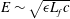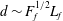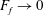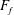We study here experimentally, numerically and using a lubrication approach, the shape, velocity and lubrication film thickness distribution of a droplet rising in a vertical Hele-Shaw cell. The droplet is surrounded by a stationary immiscible fluid and moves purely due to buoyancy. A low density difference between the two media helps to operate in a regime with capillary number $Ca$ lying between $0.03$ and $0.35$, where $Ca=\unicode[STIX]{x1D707}_{o}U_{d}/\unicode[STIX]{x1D6FE}$ is built with the surrounding oil viscosity $\unicode[STIX]{x1D707}_{o}$, the droplet velocity $U_{d}$ and surface tension $\unicode[STIX]{x1D6FE}$. The experimental data show that in this regime the droplet velocity is not influenced by the thickness of the thin lubricating film and the dynamic meniscus. For iso-viscous cases, experimental and three-dimensional numerical results of the film thickness distribution agree well with each other. The mean film thickness is well captured by the Aussillous & Quéré (Phys. Fluids, vol. 12 (10), 2000, pp. 2367–2371) model with fitting parameters. The droplet also exhibits the ‘catamaran’ shape that has been identified experimentally for a pressure-driven counterpart (Huerre et al., Phys. Rev. Lett., vol. 115 (6), 2015, 064501). This pattern has been rationalized using a two-dimensional lubrication equation. In particular, we show that this peculiar film thickness distribution is intrinsically related to the anisotropy of the fluxes induced by the droplet’s motion.

We present an experimental and numerical study of natural convection with moist air as convecting fluid. By simplifying the system as two-component convection, an experimental method is proposed for indirectly measuring the moisture transfer rates in buoyancy-driven flows. We verify the results using direct numerical simulations. It is found that the non-dimensionalized transfer rates for both sensible heat ($Nu_{T}$) and water vapour ($Nu_{e}$) are essentially determined by a generalized Grashof number $Gr$ (the ratio of combined buoyancy generated by the imposed temperature and vapour pressure gradients to viscous force), and are only weakly dependent on the buoyancy ratio $\unicode[STIX]{x1D6EC}$ (the ratio of buoyancy induced by temperature variation to that due to vapour pressure variation). Moreover, we show that the full set of control parameters $\{Gr,\unicode[STIX]{x1D6EC},Pr,Sc\}$ is more suitable than other choices for characterizing the two-component system under investigation. As a special case, the Schmidt number dependence for passive scalar transport rates in buoyancy-driven flows is also deduced.

The paper is devoted to the problem of harmonic oscillations of thin plates in a viscous incompressible fluid. The two-dimensional flows caused by the plate oscillations and their hydrodynamic influence on the plates are studied. The fluid motion is described by the non-stationary Navier–Stokes equations, which are solved numerically on the basis of the finite volume method. The simulation is carried out for plates with different thicknesses and shapes of edges in a wide range of control parameters of the oscillatory process: dimensionless frequency and amplitude of oscillations. For the first time in the framework of one model all two-dimensional flow regimes, which were found earlier in experimental studies, are described. Two new flow regimes emerging along the stability boundaries of symmetric flow regimes are localized. The map of flow regimes in the frequency–amplitude plane is constructed. The analysis of the hydrodynamic influence of flows on the plates allow us to establish new effects associated with the influence of the shape of the plates on the drag and inertia forces. Due to these effects, the values of hydrodynamic forces can differ by 90 % at the same parameters of the oscillation. The lower and upper estimates of hydrodynamic forces obtained in the work have a good agreement with the experimental data presented in the literature.

In this study, a data-driven method for the construction of a reduced-order model (ROM) for complex flows is proposed. The method uses the proper orthogonal decomposition (POD) modes as the orthogonal basis and the dynamic mode decomposition method to obtain linear equations for the temporal evolution coefficients of the modes. This method eliminates the need for the governing equations of the flows involved, and therefore saves the effort of deriving the projected equations and proving their consistency, convergence and stability, as required by the conventional Galerkin projection method, which has been successfully applied to incompressible flows but is hard to extend to compressible flows. Using a sparsity-promoting algorithm, the dimensionality of the ROM is further reduced to a minimum. The ROMs of the natural and bypass transitions of supersonic boundary layers at $Ma=2.25$ are constructed by the proposed data-driven method. The temporal evolution of the POD modes shows good agreement with that obtained by direct numerical simulations in both cases.

We consider the linear stability to axisymmetric perturbations of the family of inviscid vortex rings discovered by Norbury (J. Fluid Mech., vol. 57, 1973, pp. 417–431). Since these vortex rings are obtained as solutions to a free-boundary problem, their stability analysis is performed using recently developed methods of shape differentiation applied to the contour-dynamics formulation of the problem in the three-dimensional axisymmetric geometry. This approach allows us to systematically account for the effects of boundary deformations on the linearized evolution of the vortex ring. We investigate the instantaneous amplification of perturbations assumed to have the same the circulation as the vortex rings in their equilibrium configuration. These stability properties are then determined by the spectrum of a singular integro-differential operator defined on the vortex boundary in the meridional plane. The resulting generalized eigenvalue problem is solved numerically with a spectrally accurate discretization. Our results reveal that while thin vortex rings remain neutrally stable to axisymmetric perturbations, they become linearly unstable to such perturbations when they are sufficiently ‘fat’. Analysis of the structure of the eigenmodes demonstrates that they approach the corresponding eigenmodes of Rankine’s vortex and Hill’s vortex in the thin-vortex and fat-vortex limit, respectively. This study is a stepping stone on the way towards a complete stability analysis of inviscid vortex rings with respect to general perturbations.

The current work investigates how turbulence affects the mass transfer rate between inertial particles and fluid in a dilute, polydisperse particle system. Direct numerical simulations are performed in which all scales of turbulence are fully resolved and particles are represented in a Lagrangian reference frame. The results show that, similarly to a monodisperse system, the mass transfer rate between particles and fluid decreases as a result of particle clustering. This occurs when the flow time scale (based on the turbulence integral scale) is long relative to the chemical time scale, and is strongest when the particle time scale is one order of magnitude smaller than the flow time scale (i.e. the Stokes number is around 0.1). It is also found that for larger solid mass fractions, the clustering of the heavier particles is enhanced by the effect of drag force from the particles on the fluid (momentum back-reactions or two-way coupling). In particular, when two-way coupling is accounted for, locations of particles of different sizes are much more correlated, which leads to a stronger effect of clustering, and thus a greater reduction of the particle–fluid mass transfer rate.

The dynamics of irrotational shallow water wave turbulence forced at large scales and dissipated at small scales is investigated. First, we derive the shallow water analogue of the ‘four-fifths law’ of Kolmogorov turbulence for a third-order structure function involving velocity and displacement increments. Using this relation and assuming that the flow is dominated by shocks, we develop a simple model predicting that the shock amplitude scales as 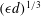$(\unicode[STIX]{x1D716}d)^{1/3}$, where $\unicode[STIX]{x1D716}$ is the mean dissipation rate and 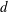$d$ the mean distance between the shocks, and that the 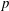$p$th-order displacement and velocity structure functions scale as 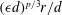$(\unicode[STIX]{x1D716}d)^{p/3}r/d$, where $r$ is the separation. Then we carry out a series of forced simulations with resolutions up to 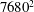$7680^{2}$, varying the Froude number, 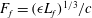$F_{f}=(\unicode[STIX]{x1D716}L_{f})^{1/3}/c$, where 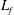$L_{f}$ is the forcing length scale and $c$ is the wave speed. In all simulations a stationary state is reached in which there is a constant spectral energy flux and equipartition between kinetic and potential energy in the constant flux range. The third-order structure function relation is satisfied with a high degree of accuracy. Mean energy is found to scale approximately as 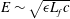$E\sim \sqrt{\unicode[STIX]{x1D716}L_{f}c}$, and is also dependent on resolution, indicating that shallow water wave turbulence does not fit into the paradigm of a Richardson–Kolmogorov cascade. In all simulations shocks develop, displayed as long thin bands of negative divergence in flow visualisations. The mean distance between the shocks is found to scale as 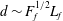$d\sim F_{f}^{1/2}L_{f}$. Structure functions of second and higher order are found to scale in good agreement with the model. We conclude that in the weak limit, 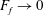$F_{f}\rightarrow 0$, shocks will become denser and weaker and finally disappear for a finite Reynolds number. On the other hand, for a given 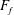$F_{f}$, no matter how small, shocks will prevail if the Reynolds number is sufficiently large.