Results from direct numerical simulations of a vertical natural convection boundary layer (NCBL) with  $Pr=0.71$ reveal that the turbulence development of such a thermally driven convective flow has two distinct stages: at relatively low Grashof number, the bulk flow is turbulent while the near-wall region is laminar-like or weakly turbulent; at sufficiently high Grashof number, the entire flow becomes turbulent in the sense of von Kármán (cf. Grossmann & Lohse, J. Fluid Mech., vol. 407, 2000, pp. 27–56, for the ultimate turbulent regime). Investigations on the turbulence statistics show that the near-wall Reynolds shear stress is negligible in the weakly turbulent regime but will grow in magnitude as the flow transitions to the ultimate regime at higher Grashof number. Similar behaviour is also seen in the streamwise turbulence intensity, where it develops from a mono-peak profile into a dual-peak structure as the Grashof number increases. At higher Grashof number, the near-wall energetic site is shown to have an energy distribution similar to that of a canonical wall-bounded turbulence (e.g. Hutchins & Marusic, Phil. Trans. R. Soc. A, vol. 365, 2007, pp. 647–664), with a peak centred at fixed location and wavelength (
$Pr=0.71$ reveal that the turbulence development of such a thermally driven convective flow has two distinct stages: at relatively low Grashof number, the bulk flow is turbulent while the near-wall region is laminar-like or weakly turbulent; at sufficiently high Grashof number, the entire flow becomes turbulent in the sense of von Kármán (cf. Grossmann & Lohse, J. Fluid Mech., vol. 407, 2000, pp. 27–56, for the ultimate turbulent regime). Investigations on the turbulence statistics show that the near-wall Reynolds shear stress is negligible in the weakly turbulent regime but will grow in magnitude as the flow transitions to the ultimate regime at higher Grashof number. Similar behaviour is also seen in the streamwise turbulence intensity, where it develops from a mono-peak profile into a dual-peak structure as the Grashof number increases. At higher Grashof number, the near-wall energetic site is shown to have an energy distribution similar to that of a canonical wall-bounded turbulence (e.g. Hutchins & Marusic, Phil. Trans. R. Soc. A, vol. 365, 2007, pp. 647–664), with a peak centred at fixed location and wavelength (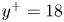 $y^+=18$ and
$y^+=18$ and 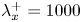 $\lambda ^+_x=1000$) in viscous coordinates. Investigation on the spanwise spectra also suggests that the turbulent near-wall streaks emerge only at sufficiently high Grashof number, with constant spacing
$\lambda ^+_x=1000$) in viscous coordinates. Investigation on the spanwise spectra also suggests that the turbulent near-wall streaks emerge only at sufficiently high Grashof number, with constant spacing  $\lambda _z^+\approx 130$. The extent of the weakly turbulent regime is identified using the maximum velocity location
$\lambda _z^+\approx 130$. The extent of the weakly turbulent regime is identified using the maximum velocity location 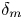 $\delta_m$ and a laminar length scale
$\delta_m$ and a laminar length scale 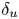 $\delta_u$. The development of near-wall turbulence is also investigated by examining the turbulence kinetic energy budget. In the weakly turbulent regime, the near-wall turbulence is sustained predominantly by the pressure transport in addition to the shear production. At higher Grashof number, the flow becomes fully turbulent, and both turbulent transport and shear production become stronger, while the pressure transport is decreased. These results also reveal that the production–dissipation ratio
$\delta_u$. The development of near-wall turbulence is also investigated by examining the turbulence kinetic energy budget. In the weakly turbulent regime, the near-wall turbulence is sustained predominantly by the pressure transport in addition to the shear production. At higher Grashof number, the flow becomes fully turbulent, and both turbulent transport and shear production become stronger, while the pressure transport is decreased. These results also reveal that the production–dissipation ratio 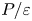 $P/\varepsilon$ of the NCBL would follow a fundamentally different trend to the canonical wall-bounded flows, which further supports that the near-wall turbulence generation is affected by the bulk flow.
$P/\varepsilon$ of the NCBL would follow a fundamentally different trend to the canonical wall-bounded flows, which further supports that the near-wall turbulence generation is affected by the bulk flow.