We use direct numerical simulation (DNS) to study drag reduction in a lubricated channel, a flow instance in which a thin layer of lubricating fluid is injected in the near-wall region so as to favour the transportation of a primary fluid. In the present configuration, the two fluids have equal density but different viscosity, so that a viscosity ratio 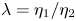 $\lambda =\eta _1/\eta _2$ can be defined. To cover a meaningful range of possible situations, we consider five different
$\lambda =\eta _1/\eta _2$ can be defined. To cover a meaningful range of possible situations, we consider five different 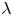 $\lambda$ in the range
$\lambda$ in the range 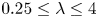 $0.25 \le \lambda \le 4$. All DNS are run using the constant power input (CPI) approach, which prescribes that the flow rate is adjusted according to the actual pressure gradient so as to keep constant the power injected into the flow. The CPI approach has been purposely extended here for the first time to the case of multiphase flows. A phase-field method is used to describe the dynamics of the liquid–liquid interface. We unambiguously show that a significant drag reduction (DR) can be achieved for
$0.25 \le \lambda \le 4$. All DNS are run using the constant power input (CPI) approach, which prescribes that the flow rate is adjusted according to the actual pressure gradient so as to keep constant the power injected into the flow. The CPI approach has been purposely extended here for the first time to the case of multiphase flows. A phase-field method is used to describe the dynamics of the liquid–liquid interface. We unambiguously show that a significant drag reduction (DR) can be achieved for 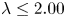 $\lambda \le 2.00$. Reportedly, the observed DR is a non-monotonic function of
$\lambda \le 2.00$. Reportedly, the observed DR is a non-monotonic function of 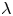 $\lambda$ and, in the present case, is maximum for
$\lambda$ and, in the present case, is maximum for 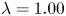 $\lambda = 1.00$ (
$\lambda = 1.00$ (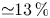 ${\simeq }13\,\%$ flow-rate increase). Upon a detailed analysis of the energy budgets, we are able to show the existence of two different DR mechanisms. For
${\simeq }13\,\%$ flow-rate increase). Upon a detailed analysis of the energy budgets, we are able to show the existence of two different DR mechanisms. For 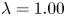 $\lambda =1.00$ and
$\lambda =1.00$ and 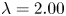 $\lambda =2.00$, DR is purely due to the effect of the surface tension – a localized elasticity element that separates the two fluids – which, decoupling the wall-normal momentum transfer mechanisms between the primary and the lubricating layer, suppresses turbulence in the lubricating layer (laminarization) and reduces the overall drag. For
$\lambda =2.00$, DR is purely due to the effect of the surface tension – a localized elasticity element that separates the two fluids – which, decoupling the wall-normal momentum transfer mechanisms between the primary and the lubricating layer, suppresses turbulence in the lubricating layer (laminarization) and reduces the overall drag. For 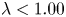 $\lambda < 1.00$, turbulence can be sustained in the lubricating layer, because of the increased local Reynolds number. In this case, DR is simply due to the smaller viscosity of the lubricating layer that acts to decrease directly the corresponding wall friction. Finally, we show evidence that an upper bound for
$\lambda < 1.00$, turbulence can be sustained in the lubricating layer, because of the increased local Reynolds number. In this case, DR is simply due to the smaller viscosity of the lubricating layer that acts to decrease directly the corresponding wall friction. Finally, we show evidence that an upper bound for 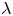 $\lambda$ exists, for which DR cannot be observed: for
$\lambda$ exists, for which DR cannot be observed: for 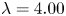 $\lambda =4.00$, we report a slight drag enhancement, thereby indicating that the turbulence suppression observed in the lubricating layer cannot completely balance the increased friction due to the larger viscosity.
$\lambda =4.00$, we report a slight drag enhancement, thereby indicating that the turbulence suppression observed in the lubricating layer cannot completely balance the increased friction due to the larger viscosity.