We study the steady force acting on a rigid spherical particle immersed in an ideal gas and impinged by a standing acoustic wave. The acoustic wavelength and particle radius are assumed much larger and smaller, respectively, than the molecular mean-free path. To analyse the system, an asymptotic scheme is constructed, combining an inviscid continuum description in the far field with a free-molecular formulation for the near gas–surface interaction. The computation yields a closed-form expression for the steady acoustic force. The free-molecular solution is compared with a formerly derived result in the continuum regime (Doinkov, Proc. R. Soc. Lond. A, vol. 447, 1994, pp. 447–466), and the latter is found characteristically larger by an order of magnitude at a given ratio between the particle radius and the acoustic wavelength. Markedly, the size of the acoustic force at ballistic flow conditions may become up to four orders of magnitude larger than the typical gravitational force, suggesting the feasibility of nano-particle acoustic levitation.

The viscoelasticity of a dilute bubble suspension is theoretically derived from the constitutive equation originally for a dilute emulsion proposed by Frankel & Acrivos (J. Fluid Mech., vol. 44, issue 1, 1970, pp. 65–78). Non-dimensionalization of the original tensor equation indicates that the viscoelasticity is systematized for a given void fraction by the capillary number $Ca$ and dynamic capillary number $Cd$, representing the bubble deformability and unsteadiness of bubble deformation. Comprehensive evaluation of the viscoelasticity according to the volume fraction, $Ca$ and $Cd$ reveals that whether the viscosity increases or decreases depends on whether $Ca$ or $Cd$ exceeds a common critical value. In addition, it is indicated that the bubble suspension has the most prominent viscoelasticity when the time scale of the shear deformation is the same as the relaxation time of the suspended bubble and when the bubbles keep a spherical shape, that is, $Ca \ll 1$ and $Cd = 1$. The applicability of this theory in flow prediction was examined in a Taylor–Couette system, and experimentally good agreement was confirmed.

The present study investigates the profiles of statistically axisymmetric turbulent jets with arbitrary buoyancy. Analytical expressions for the shape of the radial velocity, Reynolds stress and radial scalar flux profiles are derived from the governing equations by assuming self-similar Gaussian mean velocity and scalar profiles. Previously these have only been derived for the special cases of pure jets and plumes, whereas the present study generalises them to arbitrary buoyancies. These are then used to derive analytical expressions for the turbulent Schmidt/Prandtl numbers, which, along with the mean profiles, are shown to give predictions in agreement with existing literature.

The interaction between a uniform current with a circular cylinder submerged in a fluid covered by a semi-infinite ice sheet is considered analytically. The ice sheet is modelled as an elastic thin plate, and the fluid flow is described by the linearised velocity potential theory. The Green function or the velocity potential due to a source is first obtained. As the water surface is divided into two semi-infinite parts with different boundary conditions, the Wiener–Hopf method (WHM) offers significant advantages over alternative approaches and is consequently adopted. To do that, the distribution of the roots of the dispersion equation for fluid fully covered by an ice sheet in the complex plane is first analysed systematically, which does not seem to have been done before. The variations of these roots with the Froude number are investigated, especially their effects or factorisation and decomposition required in the WHM. The result is verified by comparing with that obtained from the matched eigenfunction expansion method. Through differentiating the Green function with respect to the source position, the potentials due to multipoles are obtained, which are employed to construct the velocity potential for the circular cylinder. Extensive results are provided for hydrodynamic forces on the cylinder and wave profiles, and some unique features are discussed. In particular, it is found that the forces can be highly oscillatory with the Froude number when the body is below the ice sheet, whereas such an oscillation does not exist when the body is below the free surface.

We study the behaviour of the streamwise velocity variance in turbulent wall-bounded flows using a direct numerical simulation (DNS) database of pipe flow up to friction Reynolds number ${{Re}}_{\tau } \approx 12000$. The analysis of the spanwise spectra in the viscous near-wall region strongly hints to the presence of an overlap layer between the inner- and the outer-scaled spectral ranges, featuring a $k_{\theta }^{-1+\alpha }$ decay (with $k_{\theta }$ the wavenumber in the azimuthal direction, and $\alpha \approx 0.18$), hence shallower than suggested by the classical formulation of the attached-eddy model. The key implication is that the contribution to the streamwise velocity variance $(\langle{u}^2\rangle)$ from the largest scales of motion (superstructures) slowly declines as ${{Re}}_{\tau }^{-\alpha }$, and the integrated inner-scaled variance follows a defect power law of the type $\langle u^2 \rangle ^+ = A - B \, {{Re}}_{\tau }^{-\alpha }$, with constants $A$ and $B$ depending on $y^+$. The DNS data very well support this behaviour, which implies that strict wall scaling is restored in the infinite-Reynolds-number limit. The extrapolated limit distribution of the streamwise velocity variance features a buffer-layer peak value of $\langle u^2 \rangle ^+ \approx 12.1$, and an additional outer peak with larger magnitude. The analysis of the velocity spectra also suggests a similar behaviour of the dissipation rate of the streamwise velocity variance at the wall, which is expected to attain a limiting value of approximately $0.28$, hence slightly exceeding the value $0.25$ which was assumed in previous analyses (Chen & Sreenivasan, J. Fluid Mech., vol. 908, 2021, R3). We have found evidence suggesting that the reduced near-wall influence of wall-attached eddies is likely linked to the formation of underlying turbulent Stokes layers.

Small heavy particles cannot be attracted into a region of closed streamlines in a non-accelerating frame (Sapsis & Haller, Chaos, vol. 20, issue 1, 2010, 017515). In a rotating system of vortices, however, particles can get trapped (Angilella, Physica D, vol. 239, issue 18, 2010, pp. 1789–1797) in the vicinity of vortices. We perform numerical simulations to examine trapping of inertial particles in a prototypical rotating flow described by a rotating pair of Lamb–Oseen vortices of identical strength, in the absence of gravity. Our parameter space includes the particle Stokes number 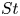$St$, which is a measure of the particle's inertia, and a density parameter 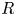$R$, which measures the particle's density relative to the fluid. In particular, we study the regime 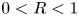$0< R<1$ and 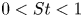$0< St<1$, which corresponds to an inertial particle that is finitely denser than the fluid. We show that in this regime, a significant fraction of particles can be trapped indefinitely close to the vortices, and display extreme clustering into objects of smaller dimension: attracting fixed points and limit cycles of different periods including chaotic attractors. As 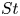$St$ increases for a given 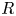$R$, we may have an incomplete or complete period-doubling route to chaos, as well as an unusual period-halving route back to a fixed point attractor. The fraction of trapped particles can be a non-monotonic function of 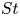$St$, and we may even have windows in 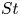$St$ for which no particle trapping occurs. At 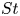$St$ larger than a critical value, beyond which trapping ceases to exist, significant fractions of particles can spend long but finite times in the vortex vicinity. The inclusion of the Basset–Boussinesq history (BBH) force is imperative in our study due to the finite density of the particle. We observe that the BBH force significantly increases the basin of attraction over which trapping occurs, and also widens the range of 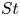$St$ for which trapping can be realised. Extreme clustering can be of significance in a host of physical applications, including planetesimal formation by aggregation of dust in protoplanetary discs, and aggregation of phytoplankton in the ocean. Our findings in the prototypical model provide impetus to conduct experiments and further numerical investigations to understand clustering of inertial particles.

The slamming wave force and pressure variabilities for monopile wave impacts are studied as functions of wave breaking shape and transverse perturbations on the breaking wave front. The impacting wave topology is characterized as slosh, flip-through, $\varOmega$, overturning and fully broken. Fifty test repetitions are conducted for each type of wave impact to assess the variability of force impulse, force and pressure. The results for the unperturbed cases show that the slamming force is highest among the nominal slosh, flip-through and $\varOmega$ tests, and that the slamming force variability is highest for the first two. We demonstrate that the slamming force and pressure variabilities decrease notably after selecting and regrouping the tests by similar crest heights and temporal slopes measured at an upstream wave gauge. The group representing $\varOmega$ wave impacts shows the largest mean slamming force and peak pressure, and their variability is the highest among all groups. Further, the effect of lateral perturbations on the pressure, force and impulse variabilities is investigated. Due to the perturbations, the slamming pressure variability for the wave impacts in which the wave front hits the monopile surface increases significantly. The variability of the slamming force is also increased for the perturbed impacts; however, it is smaller than the slamming pressure variability. The force impulse variability shows a low sensitivity to perturbations, and its magnitude is smaller than that of the force variability. Finally, the slamming pressure using fifteen pressure sensors for five selected events is studied. For these tests, oscillations at frequencies associated with structural or bubble oscillations are seen. Further, the air entertainment is documented through video recordings.

In this work, we employ well-established relations for compressible turbulent mean flows, including the velocity transformation and algebraic temperature–velocity (TV) relation, to systematically improve the algebraic Baldwin–Lomax (BL) wall model for high-speed zero-pressure-gradient air boundary layers. Any new functions or coefficients fitted by ourselves are avoided. Twelve published direct numerical simulation (DNS) datasets are employed for a priori inspiration and a posteriori examination, with Mach numbers up to 14 under adiabatic, cold and heated walls. The baseline BL model is the widely used one with semilocal scalings. Three targeted modifications are made. First, we employ a total-stress-based transformation (Griffin et al., Proc. Natl Acad. Sci. USA, vol. 118, issue 34, 2021, e2111144118) to the inner-layer eddy viscosity for improved scaling up to the logarithmic region. Second, we utilize the van Driest transformation in the outer layer based on the compressible defect velocity scaling. Third, considering the difficulty in modelling the rapidly varying and singular turbulent Prandtl number near the temperature peak in cold-wall cases, we design a two-layer strategy and use the TV relation to formulate the inner-layer temperature. Numerical results prove that the modifications take effect as designed. The prediction accuracy for mean streamwise velocity is notably improved for diabatic cases, especially in the logarithmic region. Moreover, a significant improvement in mean temperature is realized for both adiabatic and diabatic cases. The mean relative errors of temperature to DNS for all cases are down to 0.4 % in the logarithmic wall-normal coordinate and 3.4 % in the outer coordinate, around one-third of those in the baseline model.

The two-dimensional stability of vertically sheared inertial oscillations at ocean fronts is explored through a linear stability analysis and nonlinear simulations. Baroclinic effects reduce the minimum frequency of inertia-gravity waves to an extent determined by the balanced Richardson number ${{Ri}}$ of the front. Below a critical value of ${{Ri}}$, which depends on the strength of the inertial shear, the inertial oscillations become unstable to parametric subharmonic instability (PSI) resulting in growing perturbations that oscillate at half the inertial frequency $f$. Since the critical value is always greater than 1, PSI can occur at fronts stable to symmetric instability. Although modest in weak inertial shear, growth rates exceeding $f/2$ can be achieved for inertial shear greater than or equal to the thermal wind shear. Our formulation allows for non-hydrostatic perturbations and can be applied to initially unstratified geostrophic adjustment problems. We find that PSI will almost totally damp the transient oscillations that arise during geostrophic adjustment. The perturbations gain energy at the expense of the inertial oscillations through ageostrophic shear production. The perturbations then themselves become unstable to secondary Kelvin–Helmholtz instabilities creating a pathway by which the inertial oscillations can be dissipated rapidly. In contrast to symmetric and baroclinic instabilities that draw on a front's kinetic or potential energy, PSI acts to increase the energy stored in the balanced front as the convergence and divergence of the eddy-momentum fluxes set up a secondary circulation in the sense to stand up the front.

A depth-averaged, convection-dispersion equation is derived for the particle volume fraction distribution in the pressure-driven flow of a concentrated suspension of neutrally buoyant, non-colloidal particles between two parallel plates, by implementing a two-time-scale perturbation expansion of the suspension balance model (Nott & Brady, J. Fluid Mech., vol. 275, 1994, pp. 157–199) coupled with the constitutive equations of Zarraga et al. (J. Rheol., vol. 52, issue 2, 2000, pp. 185–220). The Taylor-dispersion coefficient in the macrotransport equation scales as $U_c^{\prime}B^{\prime 3}/a^{\prime 2}$, where $U_c^{\prime}$ is the characteristic depth-averaged velocity, $B^{\prime}$ is the half-depth of the channel and $a^{\prime}$ is the particle radius. Taylor dispersion relaxes gradients in the depth-averaged volume fraction along the local velocity vector. Perpendicular to the flow, however, only shear-induced migration can cause particle redistribution, leading to fluxes down gradients in volume fraction, shear rate and streamline curvature that scale as $U_c^{\prime}a^{\prime 2}/B^{\prime}$. To determine the velocity and particle distributions in Hele-Shaw suspension flows, one only needs to solve two coupled partial differential equations in the pressure and the depth-averaged volume fraction, achievable on commercially available solvers. Analogous to the macrotransport equation for suspension flow through a circular tube (Ramachandran, J. Fluid Mech., vol. 734, 2013, pp. 219–252), the evolution of the particle volume fraction distribution is dependent only on the total strain experienced by the suspension, and is independent of the suspension velocity scale. However, unlike the tube problem, a positive concentration gradient along the flow direction is susceptible to viscous miscible fingering. A linear stability analysis performed for a step increase in the volume fraction in the direction of flow with a velocity $U^{\prime}$ reveals that the growth rate and wavenumber corresponding to fastest growing mode scale as $U^{\prime}a^{\prime 2}/B^{\prime 3}$ and $a^{\prime 2/3}/B^{\prime 5/3}$, respectively.

We study the asymptotic behaviour of convective heat transfer for turbulent flows in high-porosity fluid-saturated media by two-dimensional high-resolution numerical simulation. The generalized Navier–Stokes equations for incompressible fluid flow and the heat transport equation in porous media at the representative element volume scale are solved by the lattice Boltzmann method, wherein the non-Darcian effects are taken into consideration. The asymptotic behaviour of the Nusselt number $N$ has been revealed for Rayleigh numbers $10^4\leq R\leq 10^{11}$ and Darcy numbers $10^{-6}\leq \xi \leq 10^6$: all the data for various Darcy numbers gradually collapse onto a unique line with increasing Rayleigh number. The asymptote can be well represented by $N=0.146\times R^{0.286}$ for $R>2\times 10^7$, which approaches the relationship for the Rayleigh–Bénard turbulent convection of free fluid flows. The transition can be characterized by a scaling analysis with $R^{}\xi ^{3/2}\sim 1$, below which, however, the data collapse onto the Darcy limit for porous media. The Reynolds number and the Nusselt number both increase with Darcy number above the onset of convection, whereas a premature saturation of the Nusselt number is observed in comparison with that of the Reynolds number. The counter-gradient heat transport by the large-scale flows is quantified, which compensates for the increase of the gradient heat transport with Darcy number. The heat transfer in high-porosity fluid-saturated media with a very small Darcy number $\xi \geq 10^{-6}$ can be comparable to that of free fluid flows for a sufficiently high Rayleigh number $R\geq 10^{11}$.

Experiments are conducted in an open-channel flow where half of the section is smooth and the other half consists of an array of cubes, which are either submerged or emergent. A shear layer featuring large-scale Kelvin–Helmholtz structures develops between the two subsections. The flows are first analysed in the framework of the double-averaging method (averaging of the flow both in time and space). Double averaging could be performed thanks to an experimental set-up (three-dimensional, two-component telecentric scanning particle image velocimetry) that allows to measure the velocity field in a large volume, including the interstices between the cubes. A momentum balance performed on the smooth subsection indicates that the loss of momentum towards the rough subsection has the same order of magnitude than the momentum loss through bed friction. This lateral momentum flux occurs nearly exclusively through turbulent shear stress, whereas secondary currents plays a minor role and dispersive shear stress is negligible. A pattern recognition technique is then applied to investigate statistically the large-scale Kelvin–Helmholtz structures that develop in the shear layer. The structures appear to be coherent over the water depth and to be strongly inclined in the vertical, the top part being ahead. The educed coherent structure is responsible by itself for the shape of the velocity profile across the shear layer and for a large part of the turbulence (up to 60 % for the turbulent shear stress). Finally, a coupling is identified between the passage of the Kelvin–Helmholtz structures and the instantaneous wake flow around the cubes at the interface.

We investigate the coupling effects of the two-phase interface, viscosity ratio and density ratio of the dispersed phase to the continuous phase on the flow statistics in two-phase Taylor–Couette turbulence at a system Reynolds number of $6\times 10^3$ and a system Weber number of 10 using interface-resolved three-dimensional direct numerical simulations with the volume-of-fluid method. Our study focuses on four different scenarios: neutral droplets, low-viscosity droplets, light droplets and low-viscosity light droplets. We find that neutral droplets and low-viscosity droplets primarily contribute to drag enhancement through the two-phase interface, whereas light droplets reduce the system's drag by explicitly reducing Reynolds stress due to the density dependence of Reynolds stress. In addition, low-viscosity light droplets contribute to greater drag reduction by further reducing momentum transport near the inner cylinder and implicitly reducing Reynolds stress. While interfacial tension enhances turbulent kinetic energy (TKE) transport, drag enhancement is not strongly correlated with TKE transport for both neutral droplets and low-viscosity droplets. Light droplets primarily reduce the production term by diminishing Reynolds stress, whereas the density contrast between the phases boosts TKE transport near the inner wall. Therefore, the reduction in the dissipation rate is predominantly attributed to decreased turbulence production, causing drag reduction. For low-viscosity light droplets, the production term diminishes further, primarily due to their greater reduction in Reynolds stress, while reduced viscosity weakens the density difference's contribution to TKE transport near the inner cylinder, resulting in a more pronounced reduction in the dissipation rate and consequently stronger drag reduction. Our findings provide new insights into the physics of turbulence modulation by the dispersed phase in two-phase turbulence systems.

We present direct numerical simulations of developing turbulent channel flows subjected to thermal expansion or contraction downstream of a heated or cooled wall. Using different constitutive relations for viscosity we analyse the response of variable property flows to streamwise acceleration/deceleration by separating the effect of streamwise acceleration/deceleration from the effect of wall-normal property variations. We demonstrate that, beyond a certain streamwise location, the flow can be considered in a state of ‘quasi-equilibrium’ regarding semilocally scaled variables. As such, we claim that the development of turbulent quantities due to streamwise acceleration/deceleration is localized to the region of impulsive heating/cooling, while changes in turbulence occurring farther downstream can be attributed solely to property variations. This finding allows us to study turbulence modulation in accelerating/decelerating flows using the semilocal scaling framework. By investigating the energy redistribution among the turbulent velocity fluctuations, we conclude that a change in bulk streamwise velocity has a non-local effect which originates from the change in mean shear and modifies the energy pathways through velocity-pressure-gradient correlations. On the other hand, the wall-normal property gradients have a local effect and act through the modification of the viscous dissipation. We show that it is possible to superimpose and compare the two different effects when using the semilocal scaling framework.

The interaction of opposite-signed twist waves on vortex tubes can lead to vortex bursting, a process where the core expands into a double ring-like structure with strong swirling flows. Previous works have studied vortex bursting on rectilinear vortices by axially perturbing the initial core size to generate the twist waves, and observed largely axisymmetric bursting dynamics. In this work, we numerically study bursting on vortical structures with curved centrelines, analysing the interaction between the centreline dynamics, twist wave generation and propagation, and vortex bursting. We focus on axially perturbed helical vortex tubes with small radius-to-pitch ratios up to $0.0625$, as well as vortex rings with a large radius-to-core size ratio $10$, both at a circulation-based Reynolds number $5000$. The results show that though the initial twist wave propagation speeds are relatively unaffected by the curvature and torsion of the centreline, the bursting process is altered significantly compared with rectilinear vortices. The self-induced rotation of the centreline of the helical tube induces a non-axisymmetric distortion of the bursting structure, which rapidly breaks up the vortex core into small-scale helical structures. A similar destabilization of the bursting structure also occurs on vortex rings. The enstrophy increase and accelerated energy decay associated with bursting are predominantly determined by the twist wave strength, rather than the curvature and torsion of the centreline. Combined, our findings imply that bursting could play an important role in transferring and dissipating energy of vortical structures in wakes, and turbulent flows in general.

Motivated by the recent numerical results of Khalid et al. (Phys. Rev. Lett., vol. 127, 2021, 134502), we consider the large-Weissenberg-number ($W$) asymptotics of the centre mode instability in inertialess viscoelastic channel flow. The instability is of the critical layer type in the distinguished ultra-dilute limit where $W(1-\beta )=O(1)$ as $W \rightarrow \infty$ ($\beta$ is the ratio of solvent-to-total viscosity). In contrast to centre modes in the Orr–Sommerfeld equation, $1-c=O(1)$ as $W \rightarrow \infty$, where $c$ is the phase speed normalised by the centreline speed as a central ‘outer’ region is always needed to adjust the non-zero cross-stream velocity at the critical layer down to zero at the centreline. The critical layer acts as a pair of intense ‘bellows’ which blows the flow streamlines apart locally and then sucks them back together again. This compression/rarefaction amplifies the streamwise-normal polymer stress which in turn drives the streamwise flow through local polymer stresses at the critical layer. The streamwise flow energises the cross-stream flow via continuity which in turn intensifies the critical layer to close the cycle. We also treat the large-Reynolds-number ($Re$) asymptotic structure of the upper (where $1-c=O(Re^{-2/3})$) and lower branches of the $Re$–$W$ neutral curve, confirming the inferred scalings from previous numerical computations. Finally, we remark that the viscoelastic centre-mode instability was actually first observed in viscoelastic Kolmogorov flow by Boffetta et al. (J. Fluid Mech., vol. 523, 2005, pp. 161–170).