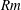 $\mathit{Rm}$ becomes three-dimensional
$\mathit{Rm}$ becomes three-dimensionalPublished online by Cambridge University Press: 18 November 2014
Magnetohydrodynamic (MHD) turbulence at low magnetic Reynolds number is experimentally investigated by studying a liquid metal flow in a cubic domain. We focus on the mechanisms that determine whether the flow is quasi-two-dimensional, three-dimensional or in any intermediate state. To this end, forcing is applied by injecting a DC current 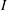 $I$ through one wall of the cube only, to drive vortices spinning along the magnetic field. Depending on the intensity of the externally applied magnetic field, these vortices extend part or all of the way through the cube. Driving the flow in this way allows us to precisely control not only the forcing intensity but also its dimensionality. A comparison with the theoretical analysis of this configuration singles out the influences of the walls and of the forcing on the flow dimensionality. Flow dimensionality is characterised in several ways. First, we show that when inertia drives three-dimensionality, the velocity near the wall where current is injected scales as
$I$ through one wall of the cube only, to drive vortices spinning along the magnetic field. Depending on the intensity of the externally applied magnetic field, these vortices extend part or all of the way through the cube. Driving the flow in this way allows us to precisely control not only the forcing intensity but also its dimensionality. A comparison with the theoretical analysis of this configuration singles out the influences of the walls and of the forcing on the flow dimensionality. Flow dimensionality is characterised in several ways. First, we show that when inertia drives three-dimensionality, the velocity near the wall where current is injected scales as 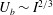 $U_{b}\sim I^{2/3}$. Second, we show that when the distance
$U_{b}\sim I^{2/3}$. Second, we show that when the distance 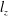 $l_{z}$ over which momentum diffuses under the action of the Lorentz force (Sommeria & Moreau, J. Fluid Mech., vol. 118, 1982, pp. 507–518) reaches the channel width
$l_{z}$ over which momentum diffuses under the action of the Lorentz force (Sommeria & Moreau, J. Fluid Mech., vol. 118, 1982, pp. 507–518) reaches the channel width 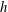 $h$, the velocity near the opposite wall
$h$, the velocity near the opposite wall 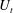 $U_{t}$ follows a similar law with a correction factor
$U_{t}$ follows a similar law with a correction factor 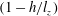 $(1-h/l_{z})$ that measures three-dimensionality. When
$(1-h/l_{z})$ that measures three-dimensionality. When 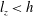 $l_{z}<h$, by contrast, the opposite wall has less influence on the flow and
$l_{z}<h$, by contrast, the opposite wall has less influence on the flow and 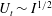 $U_{t}\sim I^{1/2}$. The central role played by the ratio
$U_{t}\sim I^{1/2}$. The central role played by the ratio 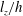 $l_{z}/h$ is confirmed by experimentally verifying the scaling
$l_{z}/h$ is confirmed by experimentally verifying the scaling 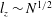 $l_{z}\sim N^{1/2}$ put forward by Sommeria & Moreau (
$l_{z}\sim N^{1/2}$ put forward by Sommeria & Moreau (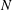 $N$ is the interaction parameter) and, finally, the nature of the three-dimensionality involved is further clarified by distinguishing weak and strong three-dimensionalities previously introduced by Klein & Pothérat (Phys. Rev. Lett., vol. 104 (3), 2010, 034502). It is found that both types vanish only asymptotically in the limit
$N$ is the interaction parameter) and, finally, the nature of the three-dimensionality involved is further clarified by distinguishing weak and strong three-dimensionalities previously introduced by Klein & Pothérat (Phys. Rev. Lett., vol. 104 (3), 2010, 034502). It is found that both types vanish only asymptotically in the limit 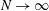 $N\rightarrow \infty$. This provides evidence that because of the no-slip walls, (i) the transition between quasi-two-dimensional and three-dimensional turbulence does not result from a global instability of the flow, unlike in domains with non-dissipative boundaries (Boeck et al. Phys. Rev. Lett., vol. 101, 2008, 244501), and (ii) it does not occur simultaneously at all scales.
$N\rightarrow \infty$. This provides evidence that because of the no-slip walls, (i) the transition between quasi-two-dimensional and three-dimensional turbulence does not result from a global instability of the flow, unlike in domains with non-dissipative boundaries (Boeck et al. Phys. Rev. Lett., vol. 101, 2008, 244501), and (ii) it does not occur simultaneously at all scales.