Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Korotkevich, A. O.
2008.
Simultaneous Numerical Simulation of Direct and Inverse Cascades in Wave Turbulence.
Physical Review Letters,
Vol. 101,
Issue. 7,
Lamont-Smith, T.
and
Waseda, T.
2008.
Wind Wave Growth at Short Fetch.
Journal of Physical Oceanography,
Vol. 38,
Issue. 7,
p.
1597.
Waseda, Takuji
Kinoshita, Takeshi
and
Tamura, Hitoshi
2009.
Evolution of a Random Directional Wave and Freak Wave Occurrence.
Journal of Physical Oceanography,
Vol. 39,
Issue. 3,
p.
621.
Waseda, Takuji
Kinoshita, Takeshi
and
Tamura, Hitoshi
2009.
Interplay of Resonant and Quasi-Resonant Interaction of the Directional Ocean Waves.
Journal of Physical Oceanography,
Vol. 39,
Issue. 9,
p.
2351.
Annenkov, S. Y.
and
Shrira, V. I.
2009.
“Fast” Nonlinear Evolution in Wave Turbulence.
Physical Review Letters,
Vol. 102,
Issue. 2,
Balk, Alexander M.
and
Zakharov, Vladimir E.
2009.
Cascade generation of zonal flows by the drift wave turbulence.
Physics Letters A,
Vol. 373,
Issue. 44,
p.
4049.
Golitsyn, G. S.
2009.
Energy cycle of wind generated surface waves.
Doklady Earth Sciences,
Vol. 429,
Issue. 1,
p.
1337.
Golitsyn, G. S.
2010.
The energy cycle of wind waves on the sea surface.
Izvestiya, Atmospheric and Oceanic Physics,
Vol. 46,
Issue. 1,
p.
6.
Babanin, Alexander V.
Tsagareli, Kakha N.
Young, I. R.
and
Walker, David J.
2010.
Numerical Investigation of Spectral Evolution of Wind Waves. Part II: Dissipation Term and Evolution Tests.
Journal of Physical Oceanography,
Vol. 40,
Issue. 4,
p.
667.
Newell, Alan C.
and
Rumpf, Benno
2011.
Wave Turbulence.
Annual Review of Fluid Mechanics,
Vol. 43,
Issue. 1,
p.
59.
Zakharov, V. E.
and
Badulin, S. I.
2011.
On energy balance in wind-driven seas.
Doklady Earth Sciences,
Vol. 440,
Issue. 2,
p.
1440.
Wen, Fan
2011.
Study of fully developed wind wave spectrum by application of quantum statistics.
Physica A: Statistical Mechanics and its Applications,
Vol. 390,
Issue. 21-22,
p.
3855.
Golitsyn, G. S.
2011.
Coefficient of horizontal eddy diffusion of a tracer on the water surface as a function of the wave age.
Izvestiya, Atmospheric and Oceanic Physics,
Vol. 47,
Issue. 3,
p.
393.
Resio, Donald T.
Long, Charles E.
and
Perrie, William
2011.
The Role of Nonlinear Momentum Fluxes on the Evolution of Directional Wind-Wave Spectra.
Journal of Physical Oceanography,
Vol. 41,
Issue. 4,
p.
781.
GAGNAIRE-RENOU, ELODIE
BENOIT, MICHEL
and
BADULIN, SERGEI I.
2011.
On weakly turbulent scaling of wind sea in simulations of fetch-limited growth.
Journal of Fluid Mechanics,
Vol. 669,
Issue. ,
p.
178.
Nazarenko, Sergey
2011.
Wave Turbulence.
Vol. 825,
Issue. ,
p.
269.
Stiassnie, Michael
2012.
Fetch‐limited growth of wind waves.
Journal of Geophysical Research: Oceans,
Vol. 117,
Issue. C11,
Babanin, Alexander V.
and
Chalikov, Dmitry
2012.
Numerical investigation of turbulence generation in non‐breaking potential waves.
Journal of Geophysical Research: Oceans,
Vol. 117,
Issue. C11,
Badulin, S. I.
and
Grigorieva, V. G.
2012.
On discriminating swell and wind‐driven seas in Voluntary Observing Ship data.
Journal of Geophysical Research: Oceans,
Vol. 117,
Issue. C11,
Korotkevich, A.O.
2012.
Influence of the condensate and inverse cascade on the direct cascade in wave turbulence.
Mathematics and Computers in Simulation,
Vol. 82,
Issue. 7,
p.
1228.
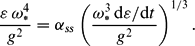 The self-similarity parameter αss was found in the numerical duration-limited experiments and was shown to be naturally varying in a relatively narrow range, being dependent on the energy growth rate only.
The self-similarity parameter αss was found in the numerical duration-limited experiments and was shown to be naturally varying in a relatively narrow range, being dependent on the energy growth rate only.