1. Introduction
The interaction of a shock wave with turbulence is a problem of fundamental interest, as well as practical relevance in high-speed flows. Turbulence affects the structure of the shock and, in return, shock significantly amplifies the turbulent fluctuations passing through it (Andreopoulos, Agui & Briassulis Reference Andreopoulos, Agui and Briassulis2000). Shock–turbulence interaction has various applications in critical engineering problems such as scramjet propulsion (Liu, Sheng & Sislian Reference Liu, Sheng and Sislian1995; Livescu & Ryu Reference Livescu and Ryu2016), inertial confinement fusion (Lele & Larsson Reference Lele and Larsson2009; Livescu & Ryu Reference Livescu and Ryu2016) and cosmic events like supernovae explosions (Ranjan, Oakley & Bonazza Reference Ranjan, Oakley and Bonazza2011). A lot of scientific effort has been spent to understand the physics of the problem and to predict the post-shock turbulence field accurately. The majority of the research is theoretical (Mahesh et al. Reference Mahesh, Lee, Lele and Moin1995; Wouchuk, de Lira & Velikovich Reference Wouchuk, de Lira and Velikovich2009; Huete Ruiz de Lira, Velikovich & Wouchuk Reference Huete Ruiz de Lira, Velikovich and Wouchuk2011; Donzis Reference Donzis2012a,Reference Donzisb; Huete Ruiz de Lira, Wouchuk & Velikovich Reference Huete Ruiz de Lira, Wouchuk and Velikovich2012; Quadros, Sinha & Larsson Reference Quadros, Sinha and Larsson2016b; Chen & Donzis Reference Chen and Donzis2019) and computational (Lee, Lele & Moin Reference Lee, Lele and Moin1993; Mahesh, Moin & Lele Reference Mahesh, Moin and Lele1996; Larsson & Lele Reference Larsson and Lele2009; Larsson, Bermejo-Moreno & Lele Reference Larsson, Bermejo-Moreno and Lele2013; Ryu & Livescu Reference Ryu and Livescu2014; Chen & Donzis Reference Chen and Donzis2019), while a limited number of experimental studies (Barre, Alem & Bonnet Reference Barre, Alem and Bonnet1996; Auvity, Barre & Bonnet Reference Auvity, Barre and Bonnet2002) have also been reported.
Small fluctuations in compressible turbulence can be represented using three fundamental modes (Kovásznay Reference Kovásznay1953): vorticity, entropy and acoustics. A theoretical method that uses this decomposition to study the interaction of homogeneous isotropic turbulence with a normal shock wave is known as linear interaction analysis (LIA) (Moore Reference Moore1954; Ribner Reference Ribner1954). LIA is linear and inviscid and uses concepts from wave physics to study the interaction between flow disturbances in one or more fundamental modes and a normal shock. The analysis assumes that the shock wave is a gas-dynamic discontinuity in the flow. LIA also relies on the assumption that the interaction time scales are small compared with the time scales of the turbulent fluctuations.
Interaction of a single vorticity wave with a shock is an elementary problem routinely used to understand the broader features of the shock–turbulence interaction. Disturbances in vorticity, with some orientation to the free stream on interacting with the shock, produce wave disturbances in all three modes, which can be analysed independently. Inter-modal interactions are not considered in LIA. The amplitudes of the modal disturbances downstream of the shock are evaluated using Rankine–Hugoniot (R-H) equations. Superposition of the modal disturbances downstream of the shock manifests the required flow fluctuations approximately for low amplitudes of the upstream vorticity wave.
Moore (Reference Moore1954) and Ribner (Reference Ribner1954) independently laid the basis for LIA several decades ago. Using Kovasznay mode decomposition (Kovásznay Reference Kovásznay1953), Moore (Reference Moore1954) studied the unsteady interaction of an acoustic wave with a normal shock and Ribner (Reference Ribner1954) investigated the interaction of a vorticity wave with a normal shock. Chang (Reference Chang1957) extended LIA by supplementing the necessary expressions for the case of interaction of entropy disturbances with a normal shock. McKenzie & Westphal (Reference McKenzie and Westphal1968) later implemented LIA theory to investigate the effect of small amplitude fluctuations in the flow interacting with an oblique shock.
In recent times, LIA has been used extensively to investigate the physical mechanisms responsible for turbulence amplification by shocks. Mahesh et al. (Reference Mahesh, Moin and Lele1996) analysed the interaction of disturbances in vorticity and entropy with a normal shock, where they considered the effect of upstream entropy fluctuations on the post-shock flow-field. Subsequently, Fabre, Jacquin & Sesterhenn (Reference Fabre, Jacquin and Sesterhenn2001) analysed the interaction of an entropy spot with a normal shock using LIA, where elementary waves of entropy fluctuations were used to construct the entropy spot. A similar approach was followed by Griffond (Reference Griffond2005) to study the effect of a mixture of gases (represented as elementary waves of fluctuating concentration) interacting with a normal shock. Recently, Quadros et al. (Reference Quadros, Sinha and Larsson2016b) investigated the turbulent energy flux generated by a normal shock and Farag, Boivin & Sagaut (Reference Farag, Boivin and Sagaut2019) studied the interaction of entropy spots with heat absorbing/releasing shock waves using LIA.
Numerical simulations provide a complementary approach to study the shock–turbulence interaction. Zang, Hussaini & Bushnell (Reference Zang, Hussaini and Bushnell1984) computed the solutions for planar waves of each of the fundamental Kovásznay modes interacting with normal shocks of varying strengths. Their analysis was restricted to incident waves making an angle of ![]() $30^{\circ }$ with the shock-normal direction. Mahesh et al. (Reference Mahesh, Moin and Lele1996) investigated individual interaction of acoustic and vorticity–entropy waves with a normal shock using direct numerical simulation (DNS). Results for turbulent kinetic energy (TKE) and vorticity variances from computations matched qualitatively with results from LIA. Recently, the works of Sethuraman, Sinha & Larsson (Reference Sethuraman, Sinha and Larsson2018), Tian et al. (Reference Tian, Jaberi, Li and Livescu2017), Quadros, Sinha & Larsson (Reference Quadros, Sinha and Larsson2016a), Quadros et al. (Reference Quadros, Sinha and Larsson2016b), Livescu & Ryu (Reference Livescu and Ryu2016), Ryu & Livescu (Reference Ryu and Livescu2014), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013) and Larsson & Lele (Reference Larsson and Lele2009) have computed the post-shock statistics of various second-moments for a range of shock Mach numbers. Results obtained from DNS are compared with LIA and a good match is found for cases with relatively low amplitude turbulent fluctuations upstream of the shock.
$30^{\circ }$ with the shock-normal direction. Mahesh et al. (Reference Mahesh, Moin and Lele1996) investigated individual interaction of acoustic and vorticity–entropy waves with a normal shock using direct numerical simulation (DNS). Results for turbulent kinetic energy (TKE) and vorticity variances from computations matched qualitatively with results from LIA. Recently, the works of Sethuraman, Sinha & Larsson (Reference Sethuraman, Sinha and Larsson2018), Tian et al. (Reference Tian, Jaberi, Li and Livescu2017), Quadros, Sinha & Larsson (Reference Quadros, Sinha and Larsson2016a), Quadros et al. (Reference Quadros, Sinha and Larsson2016b), Livescu & Ryu (Reference Livescu and Ryu2016), Ryu & Livescu (Reference Ryu and Livescu2014), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013) and Larsson & Lele (Reference Larsson and Lele2009) have computed the post-shock statistics of various second-moments for a range of shock Mach numbers. Results obtained from DNS are compared with LIA and a good match is found for cases with relatively low amplitude turbulent fluctuations upstream of the shock.
It is generally accepted that LIA predictions are valid in the limit of vanishing turbulent Mach number and infinite Reynolds number. Here, turbulent Mach number is given by ![]() $M_t = \sqrt {2k}/\bar a$,
$M_t = \sqrt {2k}/\bar a$, ![]() $k$ is the turbulent kinetic energy and
$k$ is the turbulent kinetic energy and ![]() $\bar a$ is the mean speed of sound. Many of the comparisons of LIA and DNS, either for varying
$\bar a$ is the mean speed of sound. Many of the comparisons of LIA and DNS, either for varying ![]() $M_{t}$ (Ryu & Livescu Reference Ryu and Livescu2014) or by artificially removing viscous dissipation (Larsson et al. Reference Larsson, Bermejo-Moreno and Lele2013), show this qualitative trend. However, very few quantitative estimates exist for the bounds of validity of LIA. The question as to within what range of governing parameters the results from LIA can be considered reliable is still open (Chen & Donzis Reference Chen and Donzis2019). This question has become particularly relevant in recent times, where LIA is being used as a surrogate to numerical simulations in regions of shock waves (Braun, Pullin & Meiron Reference Braun, Pullin and Meiron2019) and LIA-based turbulence models are increasingly being used in practical applications (Sinha, Mahesh & Candler Reference Sinha, Mahesh and Candler2005; Pasha & Sinha Reference Pasha and Sinha2012; Roy, Pathak & Sinha Reference Roy, Pathak and Sinha2018; Vemula & Sinha Reference Vemula and Sinha2020).
$M_{t}$ (Ryu & Livescu Reference Ryu and Livescu2014) or by artificially removing viscous dissipation (Larsson et al. Reference Larsson, Bermejo-Moreno and Lele2013), show this qualitative trend. However, very few quantitative estimates exist for the bounds of validity of LIA. The question as to within what range of governing parameters the results from LIA can be considered reliable is still open (Chen & Donzis Reference Chen and Donzis2019). This question has become particularly relevant in recent times, where LIA is being used as a surrogate to numerical simulations in regions of shock waves (Braun, Pullin & Meiron Reference Braun, Pullin and Meiron2019) and LIA-based turbulence models are increasingly being used in practical applications (Sinha, Mahesh & Candler Reference Sinha, Mahesh and Candler2005; Pasha & Sinha Reference Pasha and Sinha2012; Roy, Pathak & Sinha Reference Roy, Pathak and Sinha2018; Vemula & Sinha Reference Vemula and Sinha2020).
Lee et al. (Reference Lee, Lele and Moin1993) studied the interaction of isotropic quasi-incompressible turbulence with a weak shock wave using DNS for ![]() $1.05\leq M_1\leq 1.2$. They found that the results from LIA compare well with the DNS solution for the condition
$1.05\leq M_1\leq 1.2$. They found that the results from LIA compare well with the DNS solution for the condition ![]() $M_t^2 < 0.1(M_1^2 - 1)$. They asserted that inside the stated limit, the amplification mechanism for turbulent kinetic energy and vorticity is linear. The specified limit is valid for weak shock waves only. Similarly, Ryu & Livescu (Reference Ryu and Livescu2014) proved that the LIA solution for shock–turbulence interaction converges to DNS as
$M_t^2 < 0.1(M_1^2 - 1)$. They asserted that inside the stated limit, the amplification mechanism for turbulent kinetic energy and vorticity is linear. The specified limit is valid for weak shock waves only. Similarly, Ryu & Livescu (Reference Ryu and Livescu2014) proved that the LIA solution for shock–turbulence interaction converges to DNS as ![]() $M_{t}$ tends to smaller values. This work shows the reliability of LIA for problems involving a notable separation between turbulence scales (
$M_{t}$ tends to smaller values. This work shows the reliability of LIA for problems involving a notable separation between turbulence scales (![]() $\eta$) and shock width (
$\eta$) and shock width (![]() $\delta$), i.e. for small
$\delta$), i.e. for small ![]() $\delta /\eta \simeq 7.69M_t/Re_{\lambda }^{0.5} (M_1-1)$, which is a criteria for scale separation first given by Donzis (Reference Donzis2012a). Here,
$\delta /\eta \simeq 7.69M_t/Re_{\lambda }^{0.5} (M_1-1)$, which is a criteria for scale separation first given by Donzis (Reference Donzis2012a). Here, ![]() $Re_{\lambda }$ represents Taylor Reynolds number and
$Re_{\lambda }$ represents Taylor Reynolds number and ![]() $M_1$ is the shock Mach number. At fixed
$M_1$ is the shock Mach number. At fixed ![]() $Re_{\lambda }$ and
$Re_{\lambda }$ and ![]() $M_1$, the convergence of LIA to DNS is governed by
$M_1$, the convergence of LIA to DNS is governed by ![]() $M_t \to 0$. At higher
$M_t \to 0$. At higher ![]() $M_t$, the amplification of Reynolds stresses and vorticity is found to significantly deviate from LIA predictions, which shows the importance of nonlinear effects.
$M_t$, the amplification of Reynolds stresses and vorticity is found to significantly deviate from LIA predictions, which shows the importance of nonlinear effects.
Chen & Donzis (Reference Chen and Donzis2019) discussed a universal scaling parameter ![]() $K$ for the amplification factor of streamwise velocity, which leads to the criteria for the viability of LIA. It involves the combined effect of
$K$ for the amplification factor of streamwise velocity, which leads to the criteria for the viability of LIA. It involves the combined effect of ![]() $M_{t}$, upstream Mach number
$M_{t}$, upstream Mach number ![]() $M_1$ and an account of the viscous effects through the Reynolds number. The scaling parameter
$M_1$ and an account of the viscous effects through the Reynolds number. The scaling parameter ![]() $K$ is defined as
$K$ is defined as ![]() $K = \delta _l/ \eta$, where
$K = \delta _l/ \eta$, where ![]() $\delta _l$ is the shock thickness and
$\delta _l$ is the shock thickness and ![]() $\eta$ represents the Kolmogorov length scale. For low values of
$\eta$ represents the Kolmogorov length scale. For low values of ![]() $K$, results approach the limits specified by LIA; i.e. the amplification factor becomes a function of
$K$, results approach the limits specified by LIA; i.e. the amplification factor becomes a function of ![]() $M_1$ only. Furthermore, Grube & Martín (Reference Grube and Martín2021) studied the redistribution of energy between the transverse and streamwise Reynolds stresses in the shock–turbulence interaction using LIA and DNS. They developed a model for nonlinear interactions using LIA and the eddy viscosity approximation to quantify the redistribution of energy between transverse and streamwise Reynolds stresses.
$M_1$ only. Furthermore, Grube & Martín (Reference Grube and Martín2021) studied the redistribution of energy between the transverse and streamwise Reynolds stresses in the shock–turbulence interaction using LIA and DNS. They developed a model for nonlinear interactions using LIA and the eddy viscosity approximation to quantify the redistribution of energy between transverse and streamwise Reynolds stresses.
The objective of the current work is to address the open questions concerning LIA by analysing the elementary interaction of a vorticity wave with a normal shock both numerically and theoretically. Vorticity fluctuations are fundamental to turbulence, and they constitute one of the fundamental modes in compressible turbulence (Kovásznay Reference Kovásznay1953). Understanding the dynamics and evolution of vorticity fluctuations is crucial in high-speed applications, for instance, in studying turbulent mixing at supersonic Mach numbers in scramjet combustors, in the description of the interaction of vortex/entropy spots with normal shocks (Ribner Reference Ribner1987; Fabre et al. Reference Fabre, Jacquin and Sesterhenn2001), bubble–shock interactions and related Richtmyer–Meshkov (R–M) instability problems (Ranjan et al. Reference Ranjan, Oakley and Bonazza2011). Further, vorticity is inherently related to enstrophy, which signifies the rate of dissipation of the turbulent kinetic energy (Sinha Reference Sinha2012).
We present a weakly nonlinear framework (WNLF) for the shock–vorticity interaction and study the amplification of vorticity fluctuations across the shock wave. The analysis is an extension of the LIA framework, where we retain the second-order terms in the R-H equations across the shock wave. These terms are evaluated using the LIA solution to estimate their magnitude relative to the linear effects at the shock wave. We identify the dominant nonlinear physical mechanisms that are responsible for vorticity amplification across the shock and study their variation with the amplitude and incidence angle of the vorticity wave and the strength of the shock wave. Of particular interest are the interactions between the different Kovásznay modes and the higher-order effects of the unsteady oscillating shock wave that are neglected by the linear analysis.
The weakly nonlinear framework is validated using numerical simulations of the shock–vorticity wave interaction with the high-order accurate numerical method (Larsson & Lele Reference Larsson and Lele2009; Johnsen et al. Reference Johnsen2010). We study the deviation of the numerical results from the LIA solution for different values of the parameters listed above. The deviation is compared with the second-order vorticity amplitude predicted by WNLF. The analytical results are found to match well with the numerical data. WNLF also predicts the correct scaling of the nonlinear effects obtained from the numerical simulations. In general, other physical mechanisms in addition to the shock-induced nonlinearities could also result in nonlinear effects in vorticity. This paper focuses on studying the nonlinear interactions at the shock wave and especially strives to isolate the nonlinear effects arising from shock-induced nonlinear modal interactions. Viscous effects are assumed to be negligible in the vicinity of the shock. Both the numerical simulations and WNLF are based on the inviscid and ideal gas framework. WNLF assumes the shock to be a discontinuity, while the numerical simulations capture the shock over a few grid points. Therefore, a comparison between analytical results and the numerical solution is made very close to the numerically captured shock wave.
Finally, we use WNLF to arrive at a quantitative limit for the validity of LIA. We identify the maximum amplitude of the upstream vorticity wave, for which the nonlinear amplification of vorticity is small compared with the LIA predictions. This range is found to be a function of the shock Mach number and the incidence angle of the vorticity wave. The maximum vorticity amplitude has a non-monotonic variation with shock Mach number, with different scaling for weak and strong shock waves. The variation, as expected, depends on the dominant physical mechanisms in each case. WNLF also indicates that the LIA limit can be different for different turbulence quantities (vorticity, pressure variance, Reynolds stress, etc.). This provides a possible reason why there is no universal criteria for the validity of LIA reported in the literature.
2. Methodology
2.1. Linear interaction analysis
Let us consider a two-dimensional, small amplitude planar vorticity wave with its wavenumber vector ![]() $\boldsymbol {k}$ inclined at an angle
$\boldsymbol {k}$ inclined at an angle ![]() $\alpha$ with the
$\alpha$ with the ![]() $x$-axis (see figure 1). Mathematically, the vorticity wave can be represented as
$x$-axis (see figure 1). Mathematically, the vorticity wave can be represented as
where ![]() $\boldsymbol {r}$ is the position vector,
$\boldsymbol {r}$ is the position vector, ![]() $k$ is the magnitude of the wavenumber vector and
$k$ is the magnitude of the wavenumber vector and ![]() $\omega$ denotes the angular frequency of the vorticity wave. The quantity
$\omega$ denotes the angular frequency of the vorticity wave. The quantity ![]() $\epsilon$ is the amplitude of the vorticity wave normalized by the wavenumber and mean velocity
$\epsilon$ is the amplitude of the vorticity wave normalized by the wavenumber and mean velocity ![]() $\bar {U}_1$. The vorticity wave is advected by a one-dimensional, uniform mean flow of velocity towards the normal shock initially located along the
$\bar {U}_1$. The vorticity wave is advected by a one-dimensional, uniform mean flow of velocity towards the normal shock initially located along the ![]() $y$-axis. The shock deforms in response to the fluctuations and the local position of the unsteady shock is given by the function
$y$-axis. The shock deforms in response to the fluctuations and the local position of the unsteady shock is given by the function ![]() $\xi (y,t)$. The derivative
$\xi (y,t)$. The derivative ![]() $\xi _{y}$ thus represents the angular deformation of the shock (see figure 1).
$\xi _{y}$ thus represents the angular deformation of the shock (see figure 1).

Figure 1. Schematic of the vorticity wave–normal shock interaction showing (a) the generation of acoustic and entropy waves downstream of the shock and (b) a magnified view of the shock deformation.
Small amplitude vorticity fluctuations are solenoidal fluctuations that impose a divergence-free condition on the fluctuating velocity field. The velocity fluctuations upstream of the shock (subscript 1) are given as
where ![]() $u'$ and
$u'$ and ![]() $v'$ represent the velocity fluctuations in the shock normal (
$v'$ represent the velocity fluctuations in the shock normal (![]() $x$) and shock parallel (
$x$) and shock parallel (![]() $y$) directions, respectively. Substituting the above forms in the linearized momentum equation shows that vorticity waves do not produce pressure fluctuations in the linear, inviscid limit. Physically, because vorticity fluctuations travel with the mean flow, they do not require pressure fluctuations to advect. Also, thermodynamics dictates that the vorticity wave does not create any fluctuations in entropy in the linear limit.
$y$) directions, respectively. Substituting the above forms in the linearized momentum equation shows that vorticity waves do not produce pressure fluctuations in the linear, inviscid limit. Physically, because vorticity fluctuations travel with the mean flow, they do not require pressure fluctuations to advect. Also, thermodynamics dictates that the vorticity wave does not create any fluctuations in entropy in the linear limit.
We investigate the interaction of such vorticity fluctuations with a normal shock and obtain the perturbation field downstream using LIA. We follow the works of Fabre et al. (Reference Fabre, Jacquin and Sesterhenn2001), Mahesh et al. (Reference Mahesh, Moin and Lele1996), Moore (Reference Moore1954) and Kovásznay (Reference Kovásznay1953), and the reader may refer to these for additional details on the theory. We perform this investigation for a constant specific heat ratio of air ![]() $\gamma =1.4$.
$\gamma =1.4$.
The incident vorticity wave refracts whereas acoustic and entropy waves are generated at the shock, with inclinations ![]() $\alpha ^{p}$ and
$\alpha ^{p}$ and ![]() $\alpha ^{s}$, respectively. The refracted vorticity wave has the same inclination as that of the downstream entropy wave. Let the wavenumber of the downstream acoustic and non-acoustic waves (vorticity and entropy) be
$\alpha ^{s}$, respectively. The refracted vorticity wave has the same inclination as that of the downstream entropy wave. Let the wavenumber of the downstream acoustic and non-acoustic waves (vorticity and entropy) be ![]() $k^{p}$ and
$k^{p}$ and ![]() $k^{s}$, respectively. The post-shock acoustic wave can be either propagating or decaying depending on the angle of the incident wave. There exists a critical angle,
$k^{s}$, respectively. The post-shock acoustic wave can be either propagating or decaying depending on the angle of the incident wave. There exists a critical angle, ![]() $\alpha _{c}$ for
$\alpha _{c}$ for ![]() $\alpha \in [0,{\rm \pi} /2]$, beyond which the acoustic waves decay immediately behind the shock.
$\alpha \in [0,{\rm \pi} /2]$, beyond which the acoustic waves decay immediately behind the shock.
The linearized Euler equations with the linearized R-H conditions as the boundary conditions at the shock are solved to obtain post-shock wave characteristics. The downstream fluctuations have the same ![]() $y$ and
$y$ and ![]() $t$ dependencies as the perturbed shock front (or the incident wave) as dictated by R-H conditions. The dispersion relation at the shock constrained by the continuity equation then yields that the transverse wavenumber and the angular frequency of the wave remain invariant across the shock. Thus, we get
$t$ dependencies as the perturbed shock front (or the incident wave) as dictated by R-H conditions. The dispersion relation at the shock constrained by the continuity equation then yields that the transverse wavenumber and the angular frequency of the wave remain invariant across the shock. Thus, we get
where ![]() $r$ is the mean velocity ratio (
$r$ is the mean velocity ratio (![]() $\bar {U}_{1} / \bar {U}_{2} = \bar {\rho }_{2} / \bar {\rho }_{1}$) across the shock. The ratio
$\bar {U}_{1} / \bar {U}_{2} = \bar {\rho }_{2} / \bar {\rho }_{1}$) across the shock. The ratio ![]() $r$ is an estimate of the amount by which the streamwise wavenumber of the vorticity wave gets compressed. The wavenumber for the acoustic wave
$r$ is an estimate of the amount by which the streamwise wavenumber of the vorticity wave gets compressed. The wavenumber for the acoustic wave ![]() $k^{p}$ is then determined from the acoustic wave equation; details are given by Mahesh et al. (Reference Mahesh, Lee, Lele and Moin1995).
$k^{p}$ is then determined from the acoustic wave equation; details are given by Mahesh et al. (Reference Mahesh, Lee, Lele and Moin1995).
The disturbance field downstream of the shock (subscript 2) can be written in terms of the vorticity fluctuations ![]() $\varOmega '_2$, entropy fluctuations
$\varOmega '_2$, entropy fluctuations ![]() $s'_2$ and pressure fluctuations
$s'_2$ and pressure fluctuations ![]() $p'_2$ as
$p'_2$ as
where ![]() $Z_{vv}$,
$Z_{vv}$, ![]() $Z_{vs}$,
$Z_{vs}$, ![]() $Z_{vp}$ are the corresponding transfer coefficients and are functions of
$Z_{vp}$ are the corresponding transfer coefficients and are functions of ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$. The quantities
$M_1$. The quantities ![]() $c_p$,
$c_p$, ![]() $\bar {P}_2$ and
$\bar {P}_2$ and ![]() $\eta$ represent the specific heat of fluid, mean pressure downstream of the shock and decay parameter of acoustic wave amplitude normal to the shock, respectively. Under the assumptions of LIA, decay of pressure perturbations at the shock (
$\eta$ represent the specific heat of fluid, mean pressure downstream of the shock and decay parameter of acoustic wave amplitude normal to the shock, respectively. Under the assumptions of LIA, decay of pressure perturbations at the shock (![]() $\eta \neq 0$) occurs when
$\eta \neq 0$) occurs when ![]() $\alpha$ exceeds
$\alpha$ exceeds ![]() $\alpha _c$.
$\alpha _c$.
Both vorticity and acoustic modes of fluctuations generate velocity fluctuations downstream of the shock wave independent of each other in the linear limit. Accordingly, shock normal (![]() $u_2'$) and shock parallel (
$u_2'$) and shock parallel (![]() $v_2'$) velocity fluctuations downstream can be written as
$v_2'$) velocity fluctuations downstream can be written as
where ![]() $\zeta$ is a function of the decaying parameter (
$\zeta$ is a function of the decaying parameter (![]() $\eta$). The first and second terms on the right-hand side of (2.8) and 2.9 represent the contribution from vorticity mode and acoustic mode, respectively.
$\eta$). The first and second terms on the right-hand side of (2.8) and 2.9 represent the contribution from vorticity mode and acoustic mode, respectively.
Corrugation of the shock measured with respect to its mean position is given as
where ![]() $Z_{vx}$ is the transfer coefficient for shock perturbation. Differentiating with respect to time gives the instantaneous shock corrugation speed in the streamwise direction:
$Z_{vx}$ is the transfer coefficient for shock perturbation. Differentiating with respect to time gives the instantaneous shock corrugation speed in the streamwise direction:
Substituting these expressions in the linearized Euler equations allows the estimation of the transfer coefficients of the disturbance (![]() $Z_{vv}$,
$Z_{vv}$, ![]() $Z_{vx}$,
$Z_{vx}$, ![]() $Z_{vp}$ and
$Z_{vp}$ and ![]() $Z_{vs}$) for the post-shock regime. Mathematically, these transfer coefficients are computed as
$Z_{vs}$) for the post-shock regime. Mathematically, these transfer coefficients are computed as
 \begin{equation} A\left({\begin{array}{@{}c@{}} Z_{vv}\\ Z_{vs}\\ Z_{vp}\\ Z_{vx} \end{array}}\right)=\left(\begin{array}{@{}c@{}} -1 \\ -r\\ 0\\ \dfrac{r^2}{(\gamma - 1)M^2_1} \end{array}\right), \end{equation}
\begin{equation} A\left({\begin{array}{@{}c@{}} Z_{vv}\\ Z_{vs}\\ Z_{vp}\\ Z_{vx} \end{array}}\right)=\left(\begin{array}{@{}c@{}} -1 \\ -r\\ 0\\ \dfrac{r^2}{(\gamma - 1)M^2_1} \end{array}\right), \end{equation}where
 \begin{equation} A = \left(\begin{array}{@{}ccccccc@{}} {\sin{\alpha^s}} & -1 & \dfrac{1}{\gamma}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & \textrm{i}(r-1){\cos{\alpha^p}}\\ 2{\sin{\alpha^s}} & -1 & \dfrac{M^2_2+1}{\gamma M^2_2}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & 0 \\ -{\cos{\alpha^s}} & 0 & \dfrac{ {\sin{\alpha^p}}}{\gamma M_2 \zeta} & \textrm{i}(1-r){\sin{\alpha}}\\ {\sin{\alpha^s}} & \dfrac{1}{(\gamma-1)M^2_2} & \dfrac{1}{\gamma M^2_2}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & \textrm{i}r(r-1){\cos{\alpha^p}} \end{array}\right). \end{equation}
\begin{equation} A = \left(\begin{array}{@{}ccccccc@{}} {\sin{\alpha^s}} & -1 & \dfrac{1}{\gamma}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & \textrm{i}(r-1){\cos{\alpha^p}}\\ 2{\sin{\alpha^s}} & -1 & \dfrac{M^2_2+1}{\gamma M^2_2}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & 0 \\ -{\cos{\alpha^s}} & 0 & \dfrac{ {\sin{\alpha^p}}}{\gamma M_2 \zeta} & \textrm{i}(1-r){\sin{\alpha}}\\ {\sin{\alpha^s}} & \dfrac{1}{(\gamma-1)M^2_2} & \dfrac{1}{\gamma M^2_2}+ \dfrac{{\cos{\alpha^p}}+\textrm{i}\eta}{\gamma M_2 \zeta} & \textrm{i}r(r-1){\cos{\alpha^p}} \end{array}\right). \end{equation} Figure 2(a) shows the variation of the transfer coefficients with ![]() $\alpha$ for a fixed
$\alpha$ for a fixed ![]() $M_1$. The transfer coefficients for vorticity
$M_1$. The transfer coefficients for vorticity ![]() $Z_{vv}$ and shock deformation
$Z_{vv}$ and shock deformation ![]() $Z_{vx}$ show a monotonic increase with
$Z_{vx}$ show a monotonic increase with ![]() $\alpha$ in the propagating regime (
$\alpha$ in the propagating regime (![]() $\alpha <\alpha _c$), reaching a maximum at
$\alpha <\alpha _c$), reaching a maximum at ![]() $\alpha _c$. They decrease with further increase of
$\alpha _c$. They decrease with further increase of ![]() $\alpha$ in the decaying regime. Transfer coefficients for pressure and entropy have a non-monotonic variation in the propagative regime. For all
$\alpha$ in the decaying regime. Transfer coefficients for pressure and entropy have a non-monotonic variation in the propagative regime. For all ![]() $M_1$ and
$M_1$ and ![]() $\alpha$, LIA predicts that
$\alpha$, LIA predicts that ![]() $Z_{vv}$ is the largest, which indicates that the linear processes are dominated by vorticity amplification (see figures 2(a) and 2(b)). In the limit of a vanishing shock wave (
$Z_{vv}$ is the largest, which indicates that the linear processes are dominated by vorticity amplification (see figures 2(a) and 2(b)). In the limit of a vanishing shock wave (![]() $M_1 = 1$), there is no amplification of vorticity (
$M_1 = 1$), there is no amplification of vorticity (![]() $Z_{vv} =1$) and
$Z_{vv} =1$) and ![]() $Z_{vv}$ increases in magnitude for increases in
$Z_{vv}$ increases in magnitude for increases in ![]() $M_1$ to reach an asymptotic value as
$M_1$ to reach an asymptotic value as ![]() $M_1 \to \infty$.
$M_1 \to \infty$.

Figure 2. Variation of transfer coefficients with (a) ![]() $\alpha$ at
$\alpha$ at ![]() $M_1=3$ and (b)
$M_1=3$ and (b) ![]() $M_1$ at
$M_1$ at ![]() $\alpha =30^\circ$. Dashed red line in panel (a) indicates
$\alpha =30^\circ$. Dashed red line in panel (a) indicates ![]() $\alpha _c$.
$\alpha _c$.
The relative magnitude of the transfer coefficients and their variation with ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$ play an important role in the weakly nonlinear framework (WNLF) presented subsequently. The high values of
$M_1$ play an important role in the weakly nonlinear framework (WNLF) presented subsequently. The high values of ![]() $Z_{vv}$ and
$Z_{vv}$ and ![]() $Z_{vx}$ in the vicinity of
$Z_{vx}$ in the vicinity of ![]() $\alpha _c$ degrade the accuracy of the numerical solution presented in the paper. Hence, we restrict our numerical simulations to low values of
$\alpha _c$ degrade the accuracy of the numerical solution presented in the paper. Hence, we restrict our numerical simulations to low values of ![]() $\alpha$ in the propagating regime away from
$\alpha$ in the propagating regime away from ![]() $\alpha _c$.
$\alpha _c$.
2.2. Numerical simulations
The interaction of the vorticity wave with a normal shock is studied numerically over a two-dimensional domain, as shown in figure 3. The length of the computational domain is ![]() $4{\rm \pi}$ and
$4{\rm \pi}$ and ![]() $2{\rm \pi}$ in the streamwise (
$2{\rm \pi}$ in the streamwise (![]() $x$) and transverse (
$x$) and transverse (![]() $y$) directions, respectively. Four stations in the
$y$) directions, respectively. Four stations in the ![]() $x$-direction are marked in figure 3. We specify a supersonic boundary condition for the inflow station (
$x$-direction are marked in figure 3. We specify a supersonic boundary condition for the inflow station (![]() $x=-{\rm \pi}$), where velocity fluctuations
$x=-{\rm \pi}$), where velocity fluctuations
are superimposed on a one-dimensional supersonic streamwise mean flow ![]() $\bar {U}_1$. A non-reflecting subsonic boundary condition is applied at the outflow (
$\bar {U}_1$. A non-reflecting subsonic boundary condition is applied at the outflow (![]() $x=3{\rm \pi}$) and a periodic boundary condition is used for the transverse boundaries.
$x=3{\rm \pi}$) and a periodic boundary condition is used for the transverse boundaries.

Figure 3. Numerical domain: ![]() $x=-{\rm \pi}$ shows the inlet boundary;
$x=-{\rm \pi}$ shows the inlet boundary; ![]() $x=0$ is the initial position of the normal shock;
$x=0$ is the initial position of the normal shock; ![]() $x=2{\rm \pi}$ the start of a numerical sponge; and
$x=2{\rm \pi}$ the start of a numerical sponge; and ![]() $x=3{\rm \pi}$ the outlet boundary and end of the numerical sponge.
$x=3{\rm \pi}$ the outlet boundary and end of the numerical sponge.
The flow downstream of the normal shock is subsonic and allows spurious acoustic waves from the outflow boundary to propagate towards the shock. These acoustic reflections are undesirable and need to be avoided or damped. A numerical sponge similar to that prescribed by Larsson & Lele (Reference Larsson and Lele2009) and Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018) is used to achieve this. In our numerical domain, a sponge is used from ![]() $x=2{\rm \pi}$ to
$x=2{\rm \pi}$ to ![]() $x=3{\rm \pi}$ and it dampens the fluctuations to a target state defined by the R-H conditions for the mean flow.
$x=3{\rm \pi}$ and it dampens the fluctuations to a target state defined by the R-H conditions for the mean flow.
Compressible Euler equations for an ideal gas (![]() $\gamma =1.4$) are solved for various
$\gamma =1.4$) are solved for various ![]() $M_1$ using the solution-adaptive finite-difference Hybrid code (Larsson & Lele Reference Larsson and Lele2009). A fifth-order accurate WENO scheme with Roe-flux splitting is used to calculate the approximate fluxes near the shock and a sixth-order accurate central difference scheme is used for the remainder of the domain. The system of equations is integrated in time using a fourth-order accurate, explicit Runge–Kutta (RK4) scheme. Numerical shock is identified using a modified Ducros sensor (Larsson & Lele Reference Larsson and Lele2009). The shock is identified as the region where negative dilatation is greater than the low-pass filtered vorticity magnitude. This numerical procedure has been verified and validated on various problems of interest (Larsson & Lele Reference Larsson and Lele2009; Johnsen et al. Reference Johnsen2010; Larsson et al. Reference Larsson, Bermejo-Moreno and Lele2013), and additional details about the code can be found in Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018), Bermejo-Moreno et al. (Reference Bermejo-Moreno, Bodart, Larsson, Barney, Nichols and Jones2013), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013) and Larsson & Lele (Reference Larsson and Lele2009).
$M_1$ using the solution-adaptive finite-difference Hybrid code (Larsson & Lele Reference Larsson and Lele2009). A fifth-order accurate WENO scheme with Roe-flux splitting is used to calculate the approximate fluxes near the shock and a sixth-order accurate central difference scheme is used for the remainder of the domain. The system of equations is integrated in time using a fourth-order accurate, explicit Runge–Kutta (RK4) scheme. Numerical shock is identified using a modified Ducros sensor (Larsson & Lele Reference Larsson and Lele2009). The shock is identified as the region where negative dilatation is greater than the low-pass filtered vorticity magnitude. This numerical procedure has been verified and validated on various problems of interest (Larsson & Lele Reference Larsson and Lele2009; Johnsen et al. Reference Johnsen2010; Larsson et al. Reference Larsson, Bermejo-Moreno and Lele2013), and additional details about the code can be found in Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018), Bermejo-Moreno et al. (Reference Bermejo-Moreno, Bodart, Larsson, Barney, Nichols and Jones2013), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013) and Larsson & Lele (Reference Larsson and Lele2009).
Flow variables are normalized so that the upstream velocity equals the upstream Mach number (![]() $M_1$). For this purpose, we use density and sound speed upstream of the shock as characteristic variables, whereas the
$M_1$). For this purpose, we use density and sound speed upstream of the shock as characteristic variables, whereas the ![]() $y$-component of wavenumber (
$y$-component of wavenumber (![]() $k_y$) is used to normalize different length scales. Pressure is normalized using the characteristic density and sound speed, whereas vorticity is normalized using
$k_y$) is used to normalize different length scales. Pressure is normalized using the characteristic density and sound speed, whereas vorticity is normalized using ![]() $k_y$ and sound speed upstream of the shock. The equations are integrated in time with a Courant–Friedrichs–Lewy (CFL) number of 0.8, which corresponds to a flow time scale of
$k_y$ and sound speed upstream of the shock. The equations are integrated in time with a Courant–Friedrichs–Lewy (CFL) number of 0.8, which corresponds to a flow time scale of ![]() $\sim$0.003. It takes approximately 200 to 300 time steps to simulate one wave passage through the shock.
$\sim$0.003. It takes approximately 200 to 300 time steps to simulate one wave passage through the shock.
Initially, the normal shock lies at ![]() $x=0$ and oscillates in the transverse direction when fluctuations impinge on it and change the downstream pressure. Mismatch in the pressure levels downstream of the shock with that obtained from R-H conditions causes the shock to drift slowly. We use a time-dependent back-pressure controller (Larsson & Lele Reference Larsson and Lele2009) to reduce the shock movement and make it as stationary as possible around the desired location,
$x=0$ and oscillates in the transverse direction when fluctuations impinge on it and change the downstream pressure. Mismatch in the pressure levels downstream of the shock with that obtained from R-H conditions causes the shock to drift slowly. We use a time-dependent back-pressure controller (Larsson & Lele Reference Larsson and Lele2009) to reduce the shock movement and make it as stationary as possible around the desired location, ![]() $x=0$. We follow the implementation procedure prescribed by Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018) to control the movement of the shock using the back-pressure controller.
$x=0$. We follow the implementation procedure prescribed by Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018) to control the movement of the shock using the back-pressure controller.
The time taken by the initial disturbances to adjust to the boundary conditions is considered as an initial transient. We track the shock movement during this time as in Sethuraman et al. (Reference Sethuraman, Sinha and Larsson2018) to ascertain that the post-shock statistics are computed after the initial transients have passed. The flow statistics achieve a steady-state value at this point.
Post-shock statistics are collected at a fixed ![]() $x$-location by averaging over the transverse (
$x$-location by averaging over the transverse (![]() $y$) direction and time. For averaging, 61 time realizations distributed uniformly over a wave period are used. Flow statistics change negligibly when the averaging time is increased to multiple wave periods from those obtained over one wave period. This signifies that the statistics evaluated over one wave period are sufficiently time-independent, and the initial transients in the numerical simulations have vanished.
$y$) direction and time. For averaging, 61 time realizations distributed uniformly over a wave period are used. Flow statistics change negligibly when the averaging time is increased to multiple wave periods from those obtained over one wave period. This signifies that the statistics evaluated over one wave period are sufficiently time-independent, and the initial transients in the numerical simulations have vanished.
Figure 4(a) shows the variation of the root-mean-squared value of fluctuation kinetic energy (FKE) downstream of the shock computed for four different grid resolutions. The data are normalized by its upstream value to obtain the amplification across the shock. We observe a systematic grid-convergence to the finest grid and the LIA solution. We also note that FKE has a wave-like variation behind the shock. This is because post-shock velocity fluctuations have contribution both from vorticity and acoustic modes. The difference in wavenumbers of the two modes result in a periodic variation of FKE. In comparison, the upstream FKE is constant as it has contribution only from the vorticity mode.

Figure 4. Effect of grid refinement on (a) the amplification of root-mean-squared fluctuation kinetic energy (FKE) and (b) the amplification of root-mean-squared value of vorticity and FKE across the shock. Here, ![]() $N_x$ is the number of points in the streamwise direction;
$N_x$ is the number of points in the streamwise direction; ![]() $M_1=1.75$,
$M_1=1.75$, ![]() $\alpha =30^\circ$ and
$\alpha =30^\circ$ and ![]() $\epsilon =0.1$.
$\epsilon =0.1$.
In figure 4(b), the amplification of the root-mean-squared value of FKE and vorticity (![]() $\varOmega$) averaged in the transverse direction and in time as well as over one wavelength of the post-shock variation is presented for four successively refined computational grids. The data show negligible change for grid sizes
$\varOmega$) averaged in the transverse direction and in time as well as over one wavelength of the post-shock variation is presented for four successively refined computational grids. The data show negligible change for grid sizes ![]() $800\times 128$ and above. Therefore, we choose a grid size of
$800\times 128$ and above. Therefore, we choose a grid size of ![]() $800\times 128$ for our study and all subsequent numerical results presented are generated using this grid. The grid refinement study was performed for
$800\times 128$ for our study and all subsequent numerical results presented are generated using this grid. The grid refinement study was performed for ![]() $M_1= 1.75$ and
$M_1= 1.75$ and ![]() $\alpha = 30^\circ$. Comparable results are obtained (not shown) for the entire range of parameters considered in this work.
$\alpha = 30^\circ$. Comparable results are obtained (not shown) for the entire range of parameters considered in this work.
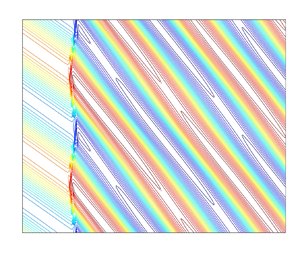
Figure 5 shows the vorticity contours computed for the shock–vorticity wave interaction at ![]() $\alpha = 30^\circ$ and
$\alpha = 30^\circ$ and ![]() $M_1 = 1.5$. Two values of
$M_1 = 1.5$. Two values of ![]() $\epsilon$ are used to highlight the effect of upstream vorticity amplitude. The numerical solution for
$\epsilon$ are used to highlight the effect of upstream vorticity amplitude. The numerical solution for ![]() $\epsilon = 0.01$ matches the vorticity pattern shown in figure 1, in terms of the refraction of the waves at the shock and the sinusoidal deformation of the shock wave. The parallel contour lines indicate two-dimensional planar waves as predicted by LIA. In comparison, the higher-amplitude interaction (
$\epsilon = 0.01$ matches the vorticity pattern shown in figure 1, in terms of the refraction of the waves at the shock and the sinusoidal deformation of the shock wave. The parallel contour lines indicate two-dimensional planar waves as predicted by LIA. In comparison, the higher-amplitude interaction (![]() $\epsilon =0.25$) shows deviation from the LIA solution downstream of the shock. The non-parallel vorticity contours, especially close to vorticity minima (around
$\epsilon =0.25$) shows deviation from the LIA solution downstream of the shock. The non-parallel vorticity contours, especially close to vorticity minima (around ![]() $-$2) indicate that the numerical solution is not a sinusoidal wave. The objective of this work is to study these nonlinear effects immediately downstream of the shock using the weakly nonlinear framework presented below.
$-$2) indicate that the numerical solution is not a sinusoidal wave. The objective of this work is to study these nonlinear effects immediately downstream of the shock using the weakly nonlinear framework presented below.

Figure 5. Vorticity contour plots at ![]() $\alpha = 30^\circ$ and
$\alpha = 30^\circ$ and ![]() $M_1 = 1.5$ for (a)
$M_1 = 1.5$ for (a) ![]() $\epsilon =0.01$ and (b)
$\epsilon =0.01$ and (b) ![]() $\epsilon =0.25$. The interaction and refraction of the vorticity wave with the shock are clearly visible. The amplitude of shock fluctuations and the nonlinearities in the downstream vorticity are larger for larger
$\epsilon =0.25$. The interaction and refraction of the vorticity wave with the shock are clearly visible. The amplitude of shock fluctuations and the nonlinearities in the downstream vorticity are larger for larger ![]() $\epsilon$.
$\epsilon$.
3. Weakly nonlinear framework
LIA, as a theory, captures the linear effects, whereas the numerical simulations contain nonlinear effects along with linear effects. In the case of a shock–turbulence interaction, nonlinear effects become significant as ![]() $\epsilon$ increases and predictions from LIA deviate from numerical simulations for large
$\epsilon$ increases and predictions from LIA deviate from numerical simulations for large ![]() $\epsilon$. It has been proposed that the interaction of linear modes leads to observed higher-order effects in vorticity and other downstream fluctuation quantities (Chu & Kovásznay Reference Chu and Kovásznay1958).
$\epsilon$. It has been proposed that the interaction of linear modes leads to observed higher-order effects in vorticity and other downstream fluctuation quantities (Chu & Kovásznay Reference Chu and Kovásznay1958).
To have more accurate predictions, these nonlinear effects need to be taken into account in the theory. We propose a framework which considers these effects quantitatively based on the modal interaction described by Chu & Kovásznay (Reference Chu and Kovásznay1958). We call it the weakly nonlinear framework (WNLF) as the analysis uses results from LIA to study nonlinear phenomena. Therefore, we expect that its applicability is restricted to weak departures from linear behaviour. As a model problem, we apply WNLF to the shock–vorticity wave interaction problem.
Consider a one-dimensional uniform mean flow up and downstream of the shock. Integration of the momentum conservation equation along the shock normal (![]() $x$) direction with the inviscid assumption gives
$x$) direction with the inviscid assumption gives
We decompose (3.1) into mean and fluctuating parts using classical Reynolds decomposition. Keeping terms up to second-order, we have
 \begin{align} & p_1' + 2\bar{\rho}_1\bar{U}_1(u_1'-\xi_t)+ \rho_1'\bar{U}_1^2+ \bar{\rho}_1(u_1'-\xi_t)^2-2\bar{\rho}_1\bar{U}_1v_1' \xi_y +2\rho_1'\bar{U}_1(u_1'-\xi_t) \nonumber\\ &\quad =p_2' + 2\bar{\rho}_2 \bar{U}_2(u_2'-\xi_t)+ \rho_2'\bar{U}_2^2+\bar{\rho}_2(u_2'-\xi_t)^2-2\bar{\rho}_2 \bar{U}_2v_2'\xi_y+2\rho_2'\bar{U}_2(u_2'-\xi_t), \end{align}
\begin{align} & p_1' + 2\bar{\rho}_1\bar{U}_1(u_1'-\xi_t)+ \rho_1'\bar{U}_1^2+ \bar{\rho}_1(u_1'-\xi_t)^2-2\bar{\rho}_1\bar{U}_1v_1' \xi_y +2\rho_1'\bar{U}_1(u_1'-\xi_t) \nonumber\\ &\quad =p_2' + 2\bar{\rho}_2 \bar{U}_2(u_2'-\xi_t)+ \rho_2'\bar{U}_2^2+\bar{\rho}_2(u_2'-\xi_t)^2-2\bar{\rho}_2 \bar{U}_2v_2'\xi_y+2\rho_2'\bar{U}_2(u_2'-\xi_t), \end{align}
where ![]() $u'-\xi _t$ represents the streamwise velocity fluctuations relative to the unsteady shock wave and
$u'-\xi _t$ represents the streamwise velocity fluctuations relative to the unsteady shock wave and ![]() $v'\xi _y$ is the component of the transverse velocity fluctuations in the shock-normal direction.
$v'\xi _y$ is the component of the transverse velocity fluctuations in the shock-normal direction.
For one-dimensional steady mean flow, the vorticity fluctuations are written in terms of the spatial gradients of velocity fluctuations, i.e.
We proceed to derive an expression for shock-downstream vorticity fluctuations in terms of the upstream flow quantities. To this end, we differentiate (3.2) to obtain ![]() $\partial u'/\partial y$ downstream of the shock as
$\partial u'/\partial y$ downstream of the shock as
 \begin{align} \bar{U}_2\frac{\partial u_2'}{\partial y} &= \bar{U}_2 \frac{\partial u_1'}{\partial y} +\bar{U}_2\frac{\partial}{\partial y} \left\{\frac{p_1'-p_2'}{2\bar{\rho}_1\bar{U}_1}+ \frac{\bar{U}_1\rho_1'}{2\bar{\rho}_1}-\frac{\bar{U}_2\rho_2'}{2\bar{\rho}_2}\right\} \nonumber\\ &\quad +\bar{U}_2\frac{\partial}{\partial y}\left\{\xi_y(v_2'-v_1') + \frac{\rho_1'(u_1'-\xi_t)}{\bar{\rho}_1}- \frac{\rho_2^{\prime}(u_2'-\xi_t)}{\bar{\rho}_2}\right\}\nonumber\\ &\quad + \bar{U}_2\frac{\partial}{\partial y}\left\{\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right\}. \end{align}
\begin{align} \bar{U}_2\frac{\partial u_2'}{\partial y} &= \bar{U}_2 \frac{\partial u_1'}{\partial y} +\bar{U}_2\frac{\partial}{\partial y} \left\{\frac{p_1'-p_2'}{2\bar{\rho}_1\bar{U}_1}+ \frac{\bar{U}_1\rho_1'}{2\bar{\rho}_1}-\frac{\bar{U}_2\rho_2'}{2\bar{\rho}_2}\right\} \nonumber\\ &\quad +\bar{U}_2\frac{\partial}{\partial y}\left\{\xi_y(v_2'-v_1') + \frac{\rho_1'(u_1'-\xi_t)}{\bar{\rho}_1}- \frac{\rho_2^{\prime}(u_2'-\xi_t)}{\bar{\rho}_2}\right\}\nonumber\\ &\quad + \bar{U}_2\frac{\partial}{\partial y}\left\{\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right\}. \end{align}
We follow the approach of Sinha (Reference Sinha2012) to derive a relation for the gradient ![]() $\partial v' /\partial x$. We write the momentum equation in the
$\partial v' /\partial x$. We write the momentum equation in the ![]() $y$-direction separately for shock upstream and downstream flow-fields and retain terms up to second-order in fluctuations, i.e.
$y$-direction separately for shock upstream and downstream flow-fields and retain terms up to second-order in fluctuations, i.e.
These two equations can be combined and rearranged to get an expression for the shock-downstream velocity gradient as
 \begin{align} \bar{U}_2\frac{\partial v_2'}{\partial x} &= \xi_{yt} {\rm \Delta}\bar{U} + \frac{1}{\bar{\rho}_1}\frac{\partial p_1'}{\partial y} -\frac{1}{\bar{\rho}_2}\frac{\partial p_2'}{\partial y} +\bar{U}_1\frac{\partial v_1'}{\partial x} -\frac{\rho_1'}{\bar{\rho}_1^2}\frac{\partial p_1'}{\partial y}+ \frac{\rho_2'}{\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y} + (u_1'-\xi_t)\frac{\partial v_1'}{\partial x}\nonumber\\ &\quad -(u_2'-\xi_t)\frac{\partial v_2'}{\partial x} + v_1' \frac{\partial v_1'}{\partial y}-v_2'\frac{\partial v_2'}{\partial y}, \end{align}
\begin{align} \bar{U}_2\frac{\partial v_2'}{\partial x} &= \xi_{yt} {\rm \Delta}\bar{U} + \frac{1}{\bar{\rho}_1}\frac{\partial p_1'}{\partial y} -\frac{1}{\bar{\rho}_2}\frac{\partial p_2'}{\partial y} +\bar{U}_1\frac{\partial v_1'}{\partial x} -\frac{\rho_1'}{\bar{\rho}_1^2}\frac{\partial p_1'}{\partial y}+ \frac{\rho_2'}{\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y} + (u_1'-\xi_t)\frac{\partial v_1'}{\partial x}\nonumber\\ &\quad -(u_2'-\xi_t)\frac{\partial v_2'}{\partial x} + v_1' \frac{\partial v_1'}{\partial y}-v_2'\frac{\partial v_2'}{\partial y}, \end{align}
where ![]() ${\rm \Delta} \bar {U} = (\bar {U}_2-\bar {U}_1)$ and the momentum conservation equation in the shock-transverse direction is used to replace time derivatives of velocity in terms of
${\rm \Delta} \bar {U} = (\bar {U}_2-\bar {U}_1)$ and the momentum conservation equation in the shock-transverse direction is used to replace time derivatives of velocity in terms of ![]() $\xi _{yt}$.
$\xi _{yt}$.
We now combine (3.4) and (3.6) to write the shock-downstream vorticity fluctuations, and collect the first and second-order terms in ![]() $\varOmega ^{(1)}$ and
$\varOmega ^{(1)}$ and ![]() $\varOmega ^{(2)}$, respectively. Because the vorticity wave upstream of the shock does not produce any density or pressure fluctuations, these are set to zero. We have
$\varOmega ^{(2)}$, respectively. Because the vorticity wave upstream of the shock does not produce any density or pressure fluctuations, these are set to zero. We have
 \begin{align} \varOmega_2^{(2)} &= \frac{(u_1'-\xi_t)}{\bar{U}_2}\frac{\partial v_1'}{\partial x} -\frac{(u_2'-\xi_t)}{\bar{U}_2}\frac{\partial v_2'}{\partial x}- \frac{\partial}{\partial y}\left[\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right] + \frac{v_1'}{\bar{U}_2}\frac{\partial v_1'}{\partial y} \nonumber\\ &\quad -\frac{v_2'}{\bar{U}_2}\frac{\partial v_2'}{\partial y}-\frac{\partial \xi_y(v_2'-v_1')}{\partial y}+ \frac{\partial}{\partial y} \frac{\rho_2'(u_2'-\xi_t)}{\bar{\rho}_2} +\frac{\rho_2'}{\bar{U}_2\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y}. \end{align}
\begin{align} \varOmega_2^{(2)} &= \frac{(u_1'-\xi_t)}{\bar{U}_2}\frac{\partial v_1'}{\partial x} -\frac{(u_2'-\xi_t)}{\bar{U}_2}\frac{\partial v_2'}{\partial x}- \frac{\partial}{\partial y}\left[\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right] + \frac{v_1'}{\bar{U}_2}\frac{\partial v_1'}{\partial y} \nonumber\\ &\quad -\frac{v_2'}{\bar{U}_2}\frac{\partial v_2'}{\partial y}-\frac{\partial \xi_y(v_2'-v_1')}{\partial y}+ \frac{\partial}{\partial y} \frac{\rho_2'(u_2'-\xi_t)}{\bar{\rho}_2} +\frac{\rho_2'}{\bar{U}_2\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y}. \end{align}
The first-order vorticity ![]() $\varOmega _2^{(1)}$ obtained from (3.7a) is analogous to the post-shock vorticity obtained from LIA, and figure 6 shows a match between the current form and that presented by Sinha (Reference Sinha2012). However,
$\varOmega _2^{(1)}$ obtained from (3.7a) is analogous to the post-shock vorticity obtained from LIA, and figure 6 shows a match between the current form and that presented by Sinha (Reference Sinha2012). However, ![]() $\varOmega _2^{(2)}$ includes the second-order nonlinear effects in shock-downstream vorticity fluctuations. The last two terms in (3.7b) represent the effects of mass flux and baroclinic generation of vorticity. These terms represent the effect of thermodynamic fluctuations downstream of the shock and their contribution is found to be negligible. This is because of the relatively small magnitude of the shock downstream entropy mode (see figure 2).
$\varOmega _2^{(2)}$ includes the second-order nonlinear effects in shock-downstream vorticity fluctuations. The last two terms in (3.7b) represent the effects of mass flux and baroclinic generation of vorticity. These terms represent the effect of thermodynamic fluctuations downstream of the shock and their contribution is found to be negligible. This is because of the relatively small magnitude of the shock downstream entropy mode (see figure 2).

Figure 6. Comparison of the first-order, shock-downstream vorticity fluctuations magnitude ![]() $|\varOmega _2^{(1)}|$ normalized by the amplitude of upstream vorticity wave
$|\varOmega _2^{(1)}|$ normalized by the amplitude of upstream vorticity wave ![]() $\epsilon$, as obtained from weakly nonlinear framework (line) and LIA (symbol) for
$\epsilon$, as obtained from weakly nonlinear framework (line) and LIA (symbol) for ![]() $\alpha =20^{\circ }$ (circle/solid line),
$\alpha =20^{\circ }$ (circle/solid line), ![]() $\alpha =30^{\circ }$ (square/dash–dotted line) and
$\alpha =30^{\circ }$ (square/dash–dotted line) and ![]() $\alpha =40^{\circ }$ (triangle/dashed line).
$\alpha =40^{\circ }$ (triangle/dashed line).
After omitting these terms, (3.7b) can be rearranged in the following form to identify the dominant physical mechanisms responsible for higher-order vorticity fluctuations downstream of the shock,
 \begin{align} \varOmega_2^{(2)}&\approx \underbrace{\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2}}_{\varOmega_a} \underbrace{-[r(v_1'+\bar{U}_1\xi_y )-(-\cot\alpha u_2'+\bar{U}_2\xi_y)]\xi_{yy}}_{\varOmega_b}\nonumber\\ &\quad +\underbrace{(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -c_d\cot\alpha(u_1'-u_2')\xi_{yy}\right]}_{\varOmega_c}, \end{align}
\begin{align} \varOmega_2^{(2)}&\approx \underbrace{\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2}}_{\varOmega_a} \underbrace{-[r(v_1'+\bar{U}_1\xi_y )-(-\cot\alpha u_2'+\bar{U}_2\xi_y)]\xi_{yy}}_{\varOmega_b}\nonumber\\ &\quad +\underbrace{(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -c_d\cot\alpha(u_1'-u_2')\xi_{yy}\right]}_{\varOmega_c}, \end{align}
where ![]() $c_d={(r+1)}/{(r-1)}$. A detailed derivation of this equation is given in Appendix A.
$c_d={(r+1)}/{(r-1)}$. A detailed derivation of this equation is given in Appendix A.
The first group of terms, denoted by ![]() $\varOmega _a$, represent the turbulent transport of vorticity fluctuations across the unsteady shock wave. The process is driven by the streamwise velocity fluctuations in the shock frame of reference
$\varOmega _a$, represent the turbulent transport of vorticity fluctuations across the unsteady shock wave. The process is driven by the streamwise velocity fluctuations in the shock frame of reference ![]() $(u'-\xi _t$) and the net convective flux of vorticity fluctuations across the shock wave is encapsulated in
$(u'-\xi _t$) and the net convective flux of vorticity fluctuations across the shock wave is encapsulated in ![]() $\varOmega _a$.
$\varOmega _a$.
The second group of terms denoted by ![]() $\varOmega _b$ is a product of the shock-transverse velocity fluctuations
$\varOmega _b$ is a product of the shock-transverse velocity fluctuations ![]() $v'+\bar U \xi _y$ with the curvature
$v'+\bar U \xi _y$ with the curvature ![]() $\xi _{yy}$ of the deformed shock wave. A curved shock is known to generate vorticity via Crocco's theorem and it appears as a second-order effect in shock–vorticity wave interaction. The curvature effect in
$\xi _{yy}$ of the deformed shock wave. A curved shock is known to generate vorticity via Crocco's theorem and it appears as a second-order effect in shock–vorticity wave interaction. The curvature effect in ![]() $\varOmega _b$ is also similar to the vorticity produced owing to the curvature of a tangential stress-free surface (Longuet-Higgins Reference Longuet-Higgins1992, Reference Longuet-Higgins1998).
$\varOmega _b$ is also similar to the vorticity produced owing to the curvature of a tangential stress-free surface (Longuet-Higgins Reference Longuet-Higgins1992, Reference Longuet-Higgins1998).
The remaining terms are grouped together as ![]() $\varOmega _c$ and it is proportional to the factor
$\varOmega _c$ and it is proportional to the factor ![]() $r-1$. Note that
$r-1$. Note that ![]() $r$ is the density ratio across the shock wave and is close to unity for weak shock waves; hence, the contribution of
$r$ is the density ratio across the shock wave and is close to unity for weak shock waves; hence, the contribution of ![]() $\varOmega _c$ is expected to be small for such cases. Figure 7 compares the amplitude of
$\varOmega _c$ is expected to be small for such cases. Figure 7 compares the amplitude of ![]() $\varOmega _2^{(2)}$ in (3.8) and the amplitude of
$\varOmega _2^{(2)}$ in (3.8) and the amplitude of ![]() $\varOmega _a+\varOmega _b$ for
$\varOmega _a+\varOmega _b$ for ![]() $\alpha =20^\circ$,
$\alpha =20^\circ$, ![]() $30^\circ$ and
$30^\circ$ and ![]() $40^\circ$. Second-order vorticity amplitude increases with
$40^\circ$. Second-order vorticity amplitude increases with ![]() $M_1$ and reaches an asymptotic limit (not shown). The plot shows
$M_1$ and reaches an asymptotic limit (not shown). The plot shows ![]() $\varOmega _c$ has negligible contribution to second-order vorticity below
$\varOmega _c$ has negligible contribution to second-order vorticity below ![]() $M_1\approx 3$. In other words, second-order contributions to shock-downstream vorticity fluctuations for lower
$M_1\approx 3$. In other words, second-order contributions to shock-downstream vorticity fluctuations for lower ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$ arise primarily from the shock curvature and turbulent flux of vorticity across the shock.
$M_1$ arise primarily from the shock curvature and turbulent flux of vorticity across the shock.

Figure 7. Variation of normalized ![]() $\varOmega _2^{(2)}$ from (3.8) (symbol) and
$\varOmega _2^{(2)}$ from (3.8) (symbol) and ![]() $\varOmega _a+\varOmega _b$ (line) at
$\varOmega _a+\varOmega _b$ (line) at ![]() $\alpha =20^\circ$ (square/solid line),
$\alpha =20^\circ$ (square/solid line), ![]() $\alpha =30^\circ$ (circle/dashed line) and
$\alpha =30^\circ$ (circle/dashed line) and ![]() $\alpha =40^\circ$ (triangle/dash–dotted line).
$\alpha =40^\circ$ (triangle/dash–dotted line).
It is easy to check that the second-order vorticity ![]() $\varOmega ^{(2)}$ given by (3.8) is proportional to
$\varOmega ^{(2)}$ given by (3.8) is proportional to ![]() $\epsilon ^2$, as terms such as
$\epsilon ^2$, as terms such as ![]() $u'$,
$u'$, ![]() $\varOmega '$,
$\varOmega '$, ![]() $\xi _t$ are proportional to
$\xi _t$ are proportional to ![]() $\epsilon$ (see § 2.1). We therefore divide
$\epsilon$ (see § 2.1). We therefore divide ![]() $\varOmega ^{(2)}$ by
$\varOmega ^{(2)}$ by ![]() $\epsilon ^2$ and further normalize it by
$\epsilon ^2$ and further normalize it by ![]() $k \bar {U}_1$ to get a non-dimensional parameter
$k \bar {U}_1$ to get a non-dimensional parameter ![]() $\phi$ that characterizes the second-order shock-downstream vorticity fluctuations,
$\phi$ that characterizes the second-order shock-downstream vorticity fluctuations,
Here, ![]() $|\cdot |$ represents complex amplitude. The complex amplitudes of
$|\cdot |$ represents complex amplitude. The complex amplitudes of ![]() $\varOmega _a$ and
$\varOmega _a$ and ![]() $\varOmega _b$ can be written in terms of the LIA transfer coefficients of vorticity
$\varOmega _b$ can be written in terms of the LIA transfer coefficients of vorticity ![]() $Z_{vv}$, pressure
$Z_{vv}$, pressure ![]() $Z_{vp}$ and shock deformation
$Z_{vp}$ and shock deformation ![]() $Z_{vx}$,
$Z_{vx}$,
 \begin{align} \frac{\mathopen| \varOmega_a \mathclose|}{\epsilon^2\bar {U}_1k} &={-}r \sin \alpha+ \sin \alpha \frac{Z_{vv}^2}{r} + \sin \alpha \left(\frac{\cos \alpha^p Z_{vv} Z_{vp}}{r\sin\alpha^s\gamma M_2\zeta} \right) \nonumber\\ &\quad - \textrm{i}Z_{vx}\cos{\alpha}\left( r-\frac{Z_{vv}\sin{\alpha}}{\sin{\alpha^s}} \right), \end{align}
\begin{align} \frac{\mathopen| \varOmega_a \mathclose|}{\epsilon^2\bar {U}_1k} &={-}r \sin \alpha+ \sin \alpha \frac{Z_{vv}^2}{r} + \sin \alpha \left(\frac{\cos \alpha^p Z_{vv} Z_{vp}}{r\sin\alpha^s\gamma M_2\zeta} \right) \nonumber\\ &\quad - \textrm{i}Z_{vx}\cos{\alpha}\left( r-\frac{Z_{vv}\sin{\alpha}}{\sin{\alpha^s}} \right), \end{align} \begin{align} \frac{\mathopen| \varOmega_b \mathclose|}{\epsilon^2\bar{U}_1k} &= \sin^2\alpha \,\textrm{i}Z_{vx} \left\{ r(-\cos\alpha +\sin\alpha \,\textrm{i}Z_{vx}) \vphantom{\left[-\cot\alpha \left(\sin\alpha^s Z_{vv}+ \frac{\cos\alpha^p Z_{vp}}{\gamma M_2\zeta}\right)+ \sin \alpha \,\textrm{i}Z_{vx}\right]}\right. \nonumber\\ &\quad \left.-\frac{1}{r}\left[-\cot\alpha \left(\sin\alpha^s Z_{vv}+ \frac{\cos\alpha^p Z_{vp}}{\gamma M_2\zeta}\right)+ \sin \alpha \,\textrm{i}Z_{vx}\right]\right\} . \end{align}
\begin{align} \frac{\mathopen| \varOmega_b \mathclose|}{\epsilon^2\bar{U}_1k} &= \sin^2\alpha \,\textrm{i}Z_{vx} \left\{ r(-\cos\alpha +\sin\alpha \,\textrm{i}Z_{vx}) \vphantom{\left[-\cot\alpha \left(\sin\alpha^s Z_{vv}+ \frac{\cos\alpha^p Z_{vp}}{\gamma M_2\zeta}\right)+ \sin \alpha \,\textrm{i}Z_{vx}\right]}\right. \nonumber\\ &\quad \left.-\frac{1}{r}\left[-\cot\alpha \left(\sin\alpha^s Z_{vv}+ \frac{\cos\alpha^p Z_{vp}}{\gamma M_2\zeta}\right)+ \sin \alpha \,\textrm{i}Z_{vx}\right]\right\} . \end{align}
In (3.10), the first term corresponds to the upstream contribution to the turbulent transport of vorticity (![]() $\varOmega _a$), while the downstream contribution to
$\varOmega _a$), while the downstream contribution to ![]() $\varOmega _a$ can be written as
$\varOmega _a$ can be written as
where the velocity fluctuation is split into its vortical (![]() $u'^{\varOmega }_2$) and acoustic (
$u'^{\varOmega }_2$) and acoustic (![]() $u'^p_2$) components. The vortical part is given by the
$u'^p_2$) components. The vortical part is given by the ![]() $Z_{vv}^2/r$ term in (3.10). However, the
$Z_{vv}^2/r$ term in (3.10). However, the ![]() $Z_{vv}Z_{vp}$ term in (3.10) corresponds to the transport of shock-downstream vorticity owing to the velocity fluctuations in the acoustic waves generated by the shock. This represents an inter-modal interaction between the post-shock vorticity and acoustic components to generate second-order vorticity fluctuations.
$Z_{vv}Z_{vp}$ term in (3.10) corresponds to the transport of shock-downstream vorticity owing to the velocity fluctuations in the acoustic waves generated by the shock. This represents an inter-modal interaction between the post-shock vorticity and acoustic components to generate second-order vorticity fluctuations.
4. Validation of weakly nonlinear framework
We present results from LIA and inviscid numerical simulations (henceforth denoted as ![]() $N$) for shock-upstream Mach numbers,
$N$) for shock-upstream Mach numbers, ![]() $M_1=\{1.25, 1.5, 1.75, 2\}$ at vorticity wave inclinations,
$M_1=\{1.25, 1.5, 1.75, 2\}$ at vorticity wave inclinations, ![]() $\alpha =\{ 20^\circ, 30^\circ, 40^\circ \}$. Higher values of
$\alpha =\{ 20^\circ, 30^\circ, 40^\circ \}$. Higher values of ![]() $M_1$ and
$M_1$ and ![]() $\alpha$ increase the numerical error, while the deviation from LIA is too low for lower values. We choose this range as numerical simulations are performed for a fixed value of shock parallel wavenumber
$\alpha$ increase the numerical error, while the deviation from LIA is too low for lower values. We choose this range as numerical simulations are performed for a fixed value of shock parallel wavenumber ![]() $k_y = 2$. The incidence angles chosen are also in the propagating regime of downstream acoustic waves.
$k_y = 2$. The incidence angles chosen are also in the propagating regime of downstream acoustic waves.
Figure 8 shows the comparison of the ![]() $y$-component of instantaneous vorticity profiles immediately downstream of the shock for
$y$-component of instantaneous vorticity profiles immediately downstream of the shock for ![]() $\epsilon =0.01$ and
$\epsilon =0.01$ and ![]() $0.2$ at
$0.2$ at ![]() $M_1=1.5$ and
$M_1=1.5$ and ![]() $\alpha =25^\circ$. The vorticity profiles are normalized with the amplitude of shock-downstream vorticity (
$\alpha =25^\circ$. The vorticity profiles are normalized with the amplitude of shock-downstream vorticity (![]() $\mathopen | \varOmega _{2}^{(1)} \mathclose |$) computed from (3.7a). Normal shock amplifies the vorticity owing to compression, and the amplification across the shock is a function of the upstream wave for a given
$\mathopen | \varOmega _{2}^{(1)} \mathclose |$) computed from (3.7a). Normal shock amplifies the vorticity owing to compression, and the amplification across the shock is a function of the upstream wave for a given ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$. Moreover, the wavelength of the vorticity wave decreases across the shock and it depends on the incidence angle
$M_1$. Moreover, the wavelength of the vorticity wave decreases across the shock and it depends on the incidence angle ![]() $\alpha$. LIA predicts sinusoidal patterns for downstream vorticity waves, and the vorticity profiles from the LIA and numerical simulations show excellent agreement for
$\alpha$. LIA predicts sinusoidal patterns for downstream vorticity waves, and the vorticity profiles from the LIA and numerical simulations show excellent agreement for ![]() $\epsilon = 0.01$. However, as we increase
$\epsilon = 0.01$. However, as we increase ![]() $\epsilon$ to
$\epsilon$ to ![]() $0.2$, vorticity profiles from numerical simulations deviate from LIA. Nonlinear effects arising from modal interactions become dominant at higher
$0.2$, vorticity profiles from numerical simulations deviate from LIA. Nonlinear effects arising from modal interactions become dominant at higher ![]() $\epsilon$, as expected.
$\epsilon$, as expected.

Figure 8. Variation of ![]() $y$-component of vorticity from LIA (solid line) and numerical simulations (dashed line) immediately downstream of the shock for (a)
$y$-component of vorticity from LIA (solid line) and numerical simulations (dashed line) immediately downstream of the shock for (a) ![]() $\epsilon =0.01$; (b)
$\epsilon =0.01$; (b) ![]() $\epsilon =0.2$, for
$\epsilon =0.2$, for ![]() $\alpha = 25^\circ$ and
$\alpha = 25^\circ$ and ![]() $M_1=1.5$. Here,
$M_1=1.5$. Here, ![]() $\varOmega '_2$ is normalized with the amplitude of
$\varOmega '_2$ is normalized with the amplitude of ![]() $\varOmega ^{(1)}_2$.
$\varOmega ^{(1)}_2$.
Figure 9 shows a similar comparison of LIA and numerical simulations at ![]() $M_1=1.25$ and
$M_1=1.25$ and ![]() $1.75$ for
$1.75$ for ![]() $\epsilon =0.2$ and
$\epsilon =0.2$ and ![]() $\alpha =25^\circ$. Vorticity profiles from LIA and numerical simulations show only a small deviation at
$\alpha =25^\circ$. Vorticity profiles from LIA and numerical simulations show only a small deviation at ![]() $M_1=1.25$, whereas the difference grows at
$M_1=1.25$, whereas the difference grows at ![]() $M_1=1.75$. This implies that the effect of nonlinear interactions at a given
$M_1=1.75$. This implies that the effect of nonlinear interactions at a given ![]() $\epsilon$ increases with
$\epsilon$ increases with ![]() $M_1$. Our goal is to study these nonlinear effects using the weakly nonlinear framework presented in the previous section for various values of shock upstream vorticity amplitude (
$M_1$. Our goal is to study these nonlinear effects using the weakly nonlinear framework presented in the previous section for various values of shock upstream vorticity amplitude (![]() $\epsilon$), Mach number (
$\epsilon$), Mach number (![]() $M_1$) and vorticity wave incidence angle (
$M_1$) and vorticity wave incidence angle (![]() $\alpha$).
$\alpha$).

Figure 9. Variation of ![]() $y$-component of vorticity from LIA (solid line) and numerical simulations (dashed line) immediately downstream of the shock for (a)
$y$-component of vorticity from LIA (solid line) and numerical simulations (dashed line) immediately downstream of the shock for (a) ![]() $M_1=1.25$; (b)
$M_1=1.25$; (b) ![]() $M_1=1.75$, for
$M_1=1.75$, for ![]() $\epsilon =0.2$,
$\epsilon =0.2$, ![]() $\alpha = 25^\circ$. Here,
$\alpha = 25^\circ$. Here, ![]() $\varOmega '_2$ is normalized with the amplitude of
$\varOmega '_2$ is normalized with the amplitude of ![]() $\varOmega ^{(1)}_2$.
$\varOmega ^{(1)}_2$.
A measure of the deviation of LIA from numerical simulations is obtained using the idea of root-mean-square (r.m.s.) error ![]() $\sigma _N$, which is calculated at a position (
$\sigma _N$, which is calculated at a position (![]() $x$) just downstream of the shock as
$x$) just downstream of the shock as
 \begin{equation} \sigma_N = \frac{1}{\bar{U}_1 k} \sqrt{\frac{1}{N_y N_t} {\sum_{m=1}^{N_t}\sum_{n=1}^{N_y} (\varOmega_{N}-\varOmega_{2}^{(1)})^2}},\end{equation}
\begin{equation} \sigma_N = \frac{1}{\bar{U}_1 k} \sqrt{\frac{1}{N_y N_t} {\sum_{m=1}^{N_t}\sum_{n=1}^{N_y} (\varOmega_{N}-\varOmega_{2}^{(1)})^2}},\end{equation}
where ![]() $\varOmega _{N}$ represents the fluctuations in vorticity obtained from numerical simulations; it includes both linear and nonlinear effects. The difference
$\varOmega _{N}$ represents the fluctuations in vorticity obtained from numerical simulations; it includes both linear and nonlinear effects. The difference ![]() $\varOmega _{N}-\varOmega _{2}^{(1)}$ thus represents the contribution of nonlinear effects. Here,
$\varOmega _{N}-\varOmega _{2}^{(1)}$ thus represents the contribution of nonlinear effects. Here, ![]() $N_y$ is the number of grid points in
$N_y$ is the number of grid points in ![]() $y$ direction and
$y$ direction and ![]() $N_t$ is the number of time instants used for calculating
$N_t$ is the number of time instants used for calculating ![]() $\sigma _N$.
$\sigma _N$.
Figure 10(a) shows the variation of ![]() $\sigma _N$ with respect to
$\sigma _N$ with respect to ![]() $x$, downstream of the shock for
$x$, downstream of the shock for ![]() $\epsilon =0.2$,
$\epsilon =0.2$, ![]() $M_1=1.5$ and
$M_1=1.5$ and ![]() $\alpha =25^\circ$. The shock lies at
$\alpha =25^\circ$. The shock lies at ![]() $x=0$, and we observe a sudden spike in
$x=0$, and we observe a sudden spike in ![]() $\sigma _N$ at that location. This is because, mathematically, the shock is a discontinuity in LIA with zero thickness, whereas the numerically captured shock spreads over multiple grid points. Calculation of
$\sigma _N$ at that location. This is because, mathematically, the shock is a discontinuity in LIA with zero thickness, whereas the numerically captured shock spreads over multiple grid points. Calculation of ![]() $\sigma _N$ inside this finite shock thickness leads to a large error, which is difficult to formalize using the present analysis. We ensure that the point used for the calculation of
$\sigma _N$ inside this finite shock thickness leads to a large error, which is difficult to formalize using the present analysis. We ensure that the point used for the calculation of ![]() $\sigma _N$ does not lie in this region.
$\sigma _N$ does not lie in this region.

Figure 10. Variation of ![]() $\sigma _N$ for
$\sigma _N$ for ![]() $\alpha =25^\circ$ and
$\alpha =25^\circ$ and ![]() $M_1=1.5$ (a) at various
$M_1=1.5$ (a) at various ![]() $x$ locations downstream of the shock for
$x$ locations downstream of the shock for ![]() $\epsilon =0.2$, (b) with
$\epsilon =0.2$, (b) with ![]() $\epsilon$ at various
$\epsilon$ at various ![]() $x$ locations:
$x$ locations: ![]() $n_x=5$ (
$n_x=5$ (![]() $x \approx 0.075$, circle);
$x \approx 0.075$, circle); ![]() $n_x =10$ (
$n_x =10$ (![]() $x \approx 0.15$, triangle);
$x \approx 0.15$, triangle); ![]() $n_x=40$ (
$n_x=40$ (![]() $x \approx 0.625$, square);
$x \approx 0.625$, square); ![]() $n_x=80$ (
$n_x=80$ (![]() $x \approx 1.25$,
$x \approx 1.25$, ![]() $+$);
$+$); ![]() $n_x =160$ (
$n_x =160$ (![]() $x \approx 2.5$, diamond).
$x \approx 2.5$, diamond).
We evaluate the variation of ![]() $\sigma _N$ at the locations indicated by black markers in figure 10(a) for various
$\sigma _N$ at the locations indicated by black markers in figure 10(a) for various ![]() $\epsilon$ (see figure 10b). The value of
$\epsilon$ (see figure 10b). The value of ![]() $\sigma _N$ immediately downstream of the shock is relatively constant over
$\sigma _N$ immediately downstream of the shock is relatively constant over ![]() $10\unicode{x2013}20$ grid points before deviating considerably. The data show the sensitivity of
$10\unicode{x2013}20$ grid points before deviating considerably. The data show the sensitivity of ![]() $\sigma _N$ to the
$\sigma _N$ to the ![]() $x$ location where it is evaluated. We choose
$x$ location where it is evaluated. We choose ![]() $x=0.075$ (
$x=0.075$ (![]() $n_x=5$) as the location downstream of the shock, where
$n_x=5$) as the location downstream of the shock, where ![]() $\sigma _N$ is evaluated in this study.
$\sigma _N$ is evaluated in this study.
The location for the evaluation of ![]() $\sigma _N$ is chosen considering its potential use in analysing shock–turbulence interaction, where the near-field is dominated by the inviscid acoustic adjustment. It is characterised by non-monotonic variation of the Reynolds stresses and is predicted well by LIA (at least for low turbulence intensities; see the work of Ryu & Livescu Reference Ryu and Livescu2014). The location of the peak turbulent kinetic energy is often used in literature (Chen & Donzis (Reference Chen and Donzis2019), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013), etc.) to study the amplification of turbulence by the shock wave. Viscous dissipation effects are found to be important downstream of the peak turbulent kinetic energy (
$\sigma _N$ is chosen considering its potential use in analysing shock–turbulence interaction, where the near-field is dominated by the inviscid acoustic adjustment. It is characterised by non-monotonic variation of the Reynolds stresses and is predicted well by LIA (at least for low turbulence intensities; see the work of Ryu & Livescu Reference Ryu and Livescu2014). The location of the peak turbulent kinetic energy is often used in literature (Chen & Donzis (Reference Chen and Donzis2019), Larsson et al. (Reference Larsson, Bermejo-Moreno and Lele2013), etc.) to study the amplification of turbulence by the shock wave. Viscous dissipation effects are found to be important downstream of the peak turbulent kinetic energy (![]() $TKE$) location. We, therefore, restrict our analysis to the region immediately downstream of the shock (
$TKE$) location. We, therefore, restrict our analysis to the region immediately downstream of the shock (![]() $n_x = 5$ or 10), so as to capture the effect of the shock directly.
$n_x = 5$ or 10), so as to capture the effect of the shock directly.
Effect of variation of the number of time instances (![]() $N_t$) used in the evaluation
$N_t$) used in the evaluation ![]() $\sigma _N$ is shown in figure 11. We start with
$\sigma _N$ is shown in figure 11. We start with ![]() $N_t=2$ and increase the number of time instances within a wave period. For
$N_t=2$ and increase the number of time instances within a wave period. For ![]() $N_t=20$, results are found to be statistically converged.
$N_t=20$, results are found to be statistically converged.

Figure 11. Variation of ![]() $\sigma _N$ with
$\sigma _N$ with ![]() $\epsilon$ for
$\epsilon$ for ![]() $\alpha =25^\circ$ and
$\alpha =25^\circ$ and ![]() $M_1=1.5$ for various total time instances (
$M_1=1.5$ for various total time instances (![]() $N_t$) over one wave period:
$N_t$) over one wave period: ![]() $N_t=2$ (dash–dotted line);
$N_t=2$ (dash–dotted line); ![]() $N_t=5$ (dashed line);
$N_t=5$ (dashed line); ![]() $N_t=10$ (solid line) and
$N_t=10$ (solid line) and ![]() $N_t=20$ (triangle).
$N_t=20$ (triangle).
4.1. Comparison with numerical simulations
Variation of ![]() $\sigma _N$ is shown in figure 12 for
$\sigma _N$ is shown in figure 12 for ![]() $\alpha = \{20^\circ,30^\circ,40^\circ \}$, for
$\alpha = \{20^\circ,30^\circ,40^\circ \}$, for ![]() $\epsilon$ ranging from
$\epsilon$ ranging from ![]() $0.01$ to
$0.01$ to ![]() $0.25$ and
$0.25$ and ![]() $M_1=\{1.25, 1.5, 1.75, 2 \}$. We notice that
$M_1=\{1.25, 1.5, 1.75, 2 \}$. We notice that ![]() $\sigma _N$ for all the cases considered increases with
$\sigma _N$ for all the cases considered increases with ![]() $\epsilon$ and
$\epsilon$ and ![]() $M_1$ for a given
$M_1$ for a given ![]() $\alpha$. The nonlinear effects are significant at higher
$\alpha$. The nonlinear effects are significant at higher ![]() $\epsilon$ and
$\epsilon$ and ![]() $M_1$ owing to the modal interaction at a given
$M_1$ owing to the modal interaction at a given ![]() $\alpha$. The results agree with the assertion of the modal interaction made by Chu & Kovásznay (Reference Chu and Kovásznay1958) with a problem involving a shock wave for the first time.
$\alpha$. The results agree with the assertion of the modal interaction made by Chu & Kovásznay (Reference Chu and Kovásznay1958) with a problem involving a shock wave for the first time.

Figure 12. Variation of ![]() $\sigma _N$ with
$\sigma _N$ with ![]() $\epsilon$ at
$\epsilon$ at ![]() $M_1=1.25$ (square),
$M_1=1.25$ (square), ![]() $M_1=1.5$ (triangle),
$M_1=1.5$ (triangle), ![]() $M_1=1.75$ (pentagon) and
$M_1=1.75$ (pentagon) and ![]() $M_1=2$ (circle) for: (a)
$M_1=2$ (circle) for: (a) ![]() $\alpha =20^\circ$; (b)
$\alpha =20^\circ$; (b) ![]() $\alpha =30^\circ$ and (c)
$\alpha =30^\circ$ and (c) ![]() $\alpha =40^\circ$.
$\alpha =40^\circ$.
We compare the deviation of the numerical solution from LIA with the second-order effects predicted by the weakly nonlinear framework in figure 13. Note that the nonlinear effects in numerical simulation ![]() $\sigma _N$ are a function of
$\sigma _N$ are a function of ![]() $\epsilon$,
$\epsilon$, ![]() $M_1$ and
$M_1$ and ![]() $\alpha$. However,
$\alpha$. However, ![]() $\phi$ includes the theoretical second-order effects of
$\phi$ includes the theoretical second-order effects of ![]() $M_1$ and
$M_1$ and ![]() $\alpha$, while the
$\alpha$, while the ![]() $\epsilon ^2$ variation of
$\epsilon ^2$ variation of ![]() $\varOmega _2^{(2)}$ is taken out from the definition of
$\varOmega _2^{(2)}$ is taken out from the definition of ![]() $\phi$. We plot the ratio
$\phi$. We plot the ratio ![]() $\sigma _N/\phi$ to study the effect of
$\sigma _N/\phi$ to study the effect of ![]() $M_1$ and
$M_1$ and ![]() $\alpha$ on the higher-order vorticity generated by the shock wave. Figure 13 shows that the Mach number variation of
$\alpha$ on the higher-order vorticity generated by the shock wave. Figure 13 shows that the Mach number variation of ![]() $\sigma _N$ is collapsed by the ratio
$\sigma _N$ is collapsed by the ratio ![]() $\sigma _N /\phi$ and the data show a clear trend of
$\sigma _N /\phi$ and the data show a clear trend of ![]() $\epsilon ^2$ variation at higher
$\epsilon ^2$ variation at higher ![]() $\epsilon$ values. There is a systematic deviation towards
$\epsilon$ values. There is a systematic deviation towards ![]() $\epsilon$ scaling in the low amplitude range and it is discussed subsequently. The
$\epsilon$ scaling in the low amplitude range and it is discussed subsequently. The ![]() $\epsilon ^2$ scaling is a direct prediction of weakly nonlinear framework and the numerical data support this finding. Moreover, the collapse of the data (for each
$\epsilon ^2$ scaling is a direct prediction of weakly nonlinear framework and the numerical data support this finding. Moreover, the collapse of the data (for each ![]() $\alpha$) shows that the Mach number scaling predicted by the theory also holds for the numerical solutions. The same is true for the
$\alpha$) shows that the Mach number scaling predicted by the theory also holds for the numerical solutions. The same is true for the ![]() $\alpha$ scaling shown in figure 14. The deviation of the numerical solution from LIA results collapse to a single curve when scaled by the second-order vorticity magnitude obtained from the weakly nonlinear framework. This collapse proves the validity of the weakly nonlinear framework.
$\alpha$ scaling shown in figure 14. The deviation of the numerical solution from LIA results collapse to a single curve when scaled by the second-order vorticity magnitude obtained from the weakly nonlinear framework. This collapse proves the validity of the weakly nonlinear framework.

Figure 13. Comparison of WNLF predictions and numerical simulations results. Variation of ![]() $\sigma _N/\phi$ for
$\sigma _N/\phi$ for ![]() $M_1=1.25$ (square),
$M_1=1.25$ (square), ![]() $M_1=1.5$ (triangle),
$M_1=1.5$ (triangle), ![]() $M_1=1.75$ (pentagon) and
$M_1=1.75$ (pentagon) and ![]() $M_1=2$ (circle) for: (a)
$M_1=2$ (circle) for: (a) ![]() $\alpha =20^\circ$; (b)
$\alpha =20^\circ$; (b) ![]() $\alpha =30^\circ$ and (c)
$\alpha =30^\circ$ and (c) ![]() $\alpha =40^\circ$. The variation of
$\alpha =40^\circ$. The variation of ![]() $\sigma _N$ with
$\sigma _N$ with ![]() $\epsilon$ collapses to a single curve when scaled by the magnitude of
$\epsilon$ collapses to a single curve when scaled by the magnitude of ![]() $\phi$. Lines show the
$\phi$. Lines show the ![]() $\epsilon ^2$ (solid) and
$\epsilon ^2$ (solid) and ![]() $\epsilon$ (dashed) variation.
$\epsilon$ (dashed) variation.

Figure 14. Collapse of the numerical data with respect to incidence angle: the ratio ![]() $\sigma _N/\phi$ for different
$\sigma _N/\phi$ for different ![]() $\alpha$ (
$\alpha$ (![]() $20^\circ$ square,
$20^\circ$ square, ![]() $30^\circ$ triangle and
$30^\circ$ triangle and ![]() $40^\circ$ circle) plotted against
$40^\circ$ circle) plotted against ![]() $\epsilon$ for different Mach numbers. Lines show the
$\epsilon$ for different Mach numbers. Lines show the ![]() $\epsilon ^2$ (solid) and
$\epsilon ^2$ (solid) and ![]() $\epsilon$ (dashed) variation with (a)
$\epsilon$ (dashed) variation with (a) ![]() $M_1=1.5$ and (b)
$M_1=1.5$ and (b) ![]() $M_1=2$.
$M_1=2$.
Figure 15 plots the difference between ![]() $\sigma _N$ and
$\sigma _N$ and ![]() $\phi$ at various
$\phi$ at various ![]() $M_1$ and
$M_1$ and ![]() $\alpha$; the data are once again scaled by
$\alpha$; the data are once again scaled by ![]() $\phi$. It is observed that the difference is in the range
$\phi$. It is observed that the difference is in the range ![]() $10^{-2}$ to
$10^{-2}$ to ![]() $10^{-4}$ and approximately varies linearly with
$10^{-4}$ and approximately varies linearly with ![]() $\epsilon$. Although the difference is small in magnitude compared with the data presented in figures 13 and 14, it is important to investigate the reasons behind this discrepancy.
$\epsilon$. Although the difference is small in magnitude compared with the data presented in figures 13 and 14, it is important to investigate the reasons behind this discrepancy.

Figure 15. The absolute error ![]() $| \sigma _N - \phi |$ scaled by
$| \sigma _N - \phi |$ scaled by ![]() $\phi$ plotted as a function of
$\phi$ plotted as a function of ![]() $\epsilon$ (a) for varying
$\epsilon$ (a) for varying ![]() $M_1$ (1.25, square; 1.5, triangle; 1.75, pentagon and 2.0, circle) for
$M_1$ (1.25, square; 1.5, triangle; 1.75, pentagon and 2.0, circle) for ![]() $\alpha =20^\circ$ and (b) for varying
$\alpha =20^\circ$ and (b) for varying ![]() $\alpha$ (
$\alpha$ (![]() $20^\circ$, square;
$20^\circ$, square; ![]() $30^\circ$, triangle and
$30^\circ$, triangle and ![]() $40^\circ$, circle) at
$40^\circ$, circle) at ![]() $M_1=2$. Line represents the
$M_1=2$. Line represents the ![]() $\epsilon$ variation.
$\epsilon$ variation.
The discrepancies between ![]() $\sigma _N$ and
$\sigma _N$ and ![]() $\phi$ are possibly related to the numerical challenges faced in the computations and the procedure used to evaluate
$\phi$ are possibly related to the numerical challenges faced in the computations and the procedure used to evaluate ![]() $\sigma _N$. The error related to numerical techniques are discussed by Johnsen et al. (Reference Johnsen2010) and have been minimized while carrying out this study. The selection of the
$\sigma _N$. The error related to numerical techniques are discussed by Johnsen et al. (Reference Johnsen2010) and have been minimized while carrying out this study. The selection of the ![]() $x$ location used to calculate
$x$ location used to calculate ![]() $\sigma _N$ downstream of the shock and the phase difference between theoretical and numerical waves upstream of the shock contributes to some error. We ensure that we minimize these errors and it is found to be of the order of
$\sigma _N$ downstream of the shock and the phase difference between theoretical and numerical waves upstream of the shock contributes to some error. We ensure that we minimize these errors and it is found to be of the order of ![]() $10^{-5}$ or smaller.
$10^{-5}$ or smaller.
Finally, and perhaps more significantly, the numerical simulations capture the unsteady oscillating shock wave on a Cartesian computational grid. This introduces errors in shock capturing owing to misalignment between the shock shape and the grid lines (Ching et al. Reference Ching, Lv, Gnoffo, Barnhardt and Ihme2019; Kitamura Reference Kitamura2013), and creates discrete jumps in the shock profile, as shown in figure 16. Note that the figure is highly magnified in the vicinity of the shock wave, such that the shock profile over two grid cells is clearly visible in terms of the pressure contours. The magnification in the ![]() $x$-direction exceeds that in the
$x$-direction exceeds that in the ![]() $y$-direction by a factor of 5. Each jump introduces an additional curvature to the numerically captured shock wave, and it generates non-physical vorticity, entropy and related quantities behind the shock. It is observed that the number of jumps in the shock wave increases proportionately with the amplitude of the shock motion (compare figures 16(a) and 16(b)). The shock amplitude, in turn, is proportional to the amplitude of the incoming vorticity wave (
$y$-direction by a factor of 5. Each jump introduces an additional curvature to the numerically captured shock wave, and it generates non-physical vorticity, entropy and related quantities behind the shock. It is observed that the number of jumps in the shock wave increases proportionately with the amplitude of the shock motion (compare figures 16(a) and 16(b)). The shock amplitude, in turn, is proportional to the amplitude of the incoming vorticity wave (![]() $\epsilon$), as per the assumption in linear theory. The shock-grid misalignment error can therefore be expected to scale linearly with
$\epsilon$), as per the assumption in linear theory. The shock-grid misalignment error can therefore be expected to scale linearly with ![]() $\epsilon$, denoted by the dashed lines in figure 15.
$\epsilon$, denoted by the dashed lines in figure 15.

Figure 16. Pressure contours show corrugations in the numerically captured shock wave on a Cartesian grid leading to shock–grid misalignment error for ![]() $\alpha =25^\circ$ and
$\alpha =25^\circ$ and ![]() $M_1=1.5$: (a)
$M_1=1.5$: (a) ![]() $\epsilon =0.1\,\%$; (b)
$\epsilon =0.1\,\%$; (b) ![]() $\epsilon =0.2\,\%$.
$\epsilon =0.2\,\%$.
Note that the sinusoidal deformation of the shock wave is an inherent feature of the shock–vorticity wave interaction. It cannot be neglected even at low values of ![]() $\epsilon$. The shock-capturing error is therefore small, but finite at low
$\epsilon$. The shock-capturing error is therefore small, but finite at low ![]() $\epsilon$. As we increase the amplitude of the upstream vorticity wave, higher-order effects become important and the scaling shifts from
$\epsilon$. As we increase the amplitude of the upstream vorticity wave, higher-order effects become important and the scaling shifts from ![]() $O(\epsilon )$ to
$O(\epsilon )$ to ![]() $O(\epsilon ^2)$ (see figures 13 and 14). After removing the
$O(\epsilon ^2)$ (see figures 13 and 14). After removing the ![]() $O(\epsilon )$ error shown in figure 15, the variation of the corrected
$O(\epsilon )$ error shown in figure 15, the variation of the corrected ![]() $\sigma _N/ \phi$ is plotted in figures 17 and 18. We find that the scaled variation now varies clearly as
$\sigma _N/ \phi$ is plotted in figures 17 and 18. We find that the scaled variation now varies clearly as ![]() $O(\epsilon ^2)$ over the entire range of parameters considered in this work.
$O(\epsilon ^2)$ over the entire range of parameters considered in this work.

Figure 17. Collapse with respect to ![]() $M_1$: the ratio
$M_1$: the ratio ![]() $\sigma _N/\phi$ after removing
$\sigma _N/\phi$ after removing ![]() $O(\epsilon )$ error for different
$O(\epsilon )$ error for different ![]() $\alpha$ (
$\alpha$ (![]() $20^\circ$, square;
$20^\circ$, square; ![]() $30^\circ$, triangle and
$30^\circ$, triangle and ![]() $40^\circ$, circle) plotted against
$40^\circ$, circle) plotted against ![]() $\epsilon$ for different Mach number. Line shows the
$\epsilon$ for different Mach number. Line shows the ![]() $\epsilon ^2$ variation.
$\epsilon ^2$ variation.

Figure 18. Variation for ![]() $\sigma _N$ scaled by the magnitude of
$\sigma _N$ scaled by the magnitude of ![]() $\phi$ with
$\phi$ with ![]() $\epsilon$ after removing
$\epsilon$ after removing ![]() $O(\epsilon )$ error for
$O(\epsilon )$ error for ![]() $\alpha =20^\circ$ (square),
$\alpha =20^\circ$ (square), ![]() $\alpha =30^\circ$ (triangle) and
$\alpha =30^\circ$ (triangle) and ![]() $\alpha =40^\circ$ (circle) for (a)
$\alpha =40^\circ$ (circle) for (a) ![]() $M_1=1.25$, (b)
$M_1=1.25$, (b) ![]() $M_1=1.5$, (c)
$M_1=1.5$, (c) ![]() $M_1=1.75$, (d)
$M_1=1.75$, (d) ![]() $M_1=2$. Solid line shows
$M_1=2$. Solid line shows ![]() $\epsilon ^2$ variation.
$\epsilon ^2$ variation.
The magnitude of ![]() $\phi$ constitutes the nonlinear effects in vorticity as given by (3.8) and follows the trend of
$\phi$ constitutes the nonlinear effects in vorticity as given by (3.8) and follows the trend of ![]() $\sigma _N$ accurately after correcting for numerical error. This means that the physics which governs nonlinear effects in vorticity as a function of
$\sigma _N$ accurately after correcting for numerical error. This means that the physics which governs nonlinear effects in vorticity as a function of ![]() $M_1$ is captured by
$M_1$ is captured by ![]() $\phi$ in the weakly nonlinear range of
$\phi$ in the weakly nonlinear range of ![]() $\epsilon \leq 0.25$. These results strongly confirm the usefulness of the weakly nonlinear framework presented in § 3.1, which is correct up to second-order in
$\epsilon \leq 0.25$. These results strongly confirm the usefulness of the weakly nonlinear framework presented in § 3.1, which is correct up to second-order in ![]() $\epsilon$.
$\epsilon$.
It is important to study the scaling of these nonlinear effects with respect to ![]() $M_1$. Existence of scaling allows the predictions of variations at different
$M_1$. Existence of scaling allows the predictions of variations at different ![]() $M_1$ without performing numerical simulations for each individual case. The results from LIA can also be improved by offsetting for the error accordingly. Scaling could be valuable for problems of the shock–turbulence interaction, where DNS of the problem at higher
$M_1$ without performing numerical simulations for each individual case. The results from LIA can also be improved by offsetting for the error accordingly. Scaling could be valuable for problems of the shock–turbulence interaction, where DNS of the problem at higher ![]() $M_1$ becomes increasingly more difficult to perform.
$M_1$ becomes increasingly more difficult to perform.
4.2. Parameter space
The weakly nonlinear framework presented in this work uses the results of LIA to study the nonlinear effects in the shock–vorticity interaction. As per LIA, the shock-downstream disturbance field is a function of the upstream vorticity wave amplitude ![]() $\epsilon$, incidence angle
$\epsilon$, incidence angle ![]() $\alpha$ and the shock strength given by the flow Mach number
$\alpha$ and the shock strength given by the flow Mach number ![]() $M_1$. We consider these three parameters for characterizing the nonlinear effects. The results from linear theory also depend on the wavenumber of the upstream wave. Here, we keep the transverse component of the upstream wavenumber constant (
$M_1$. We consider these three parameters for characterizing the nonlinear effects. The results from linear theory also depend on the wavenumber of the upstream wave. Here, we keep the transverse component of the upstream wavenumber constant (![]() $k_y = 2$). Therefore, the upstream wavenumber
$k_y = 2$). Therefore, the upstream wavenumber ![]() $k = k_y/\sin \alpha$ changes with the incidence angle.
$k = k_y/\sin \alpha$ changes with the incidence angle.
Nonlinear effects in the shock–disturbance interactions are primarily driven by the intensity of fluctuations (![]() $\epsilon$) upstream of the shock. The separation of linear and nonlinear regimes based on
$\epsilon$) upstream of the shock. The separation of linear and nonlinear regimes based on ![]() $\epsilon$ is not clearly defined for such interactions. Here, we use existing literature on the shock–turbulence interaction to guide the choice of the range of
$\epsilon$ is not clearly defined for such interactions. Here, we use existing literature on the shock–turbulence interaction to guide the choice of the range of ![]() $\epsilon$ used to study the nonlinear effects. Canonical shock–turbulence interactions are classified as lying in either a wrinkled regime or a broken shock regime. At low disturbance intensities, the shock front remains intact but has unsteady corrugation. At large values of turbulence intensities, the shock front may disappear locally, giving rise to what are called as shock holes. LIA does not predict shock holes and is therefore valid only in the wrinkled regime. The same is expected to be true for the weakly nonlinear framework that builds upon the LIA solution.
$\epsilon$ used to study the nonlinear effects. Canonical shock–turbulence interactions are classified as lying in either a wrinkled regime or a broken shock regime. At low disturbance intensities, the shock front remains intact but has unsteady corrugation. At large values of turbulence intensities, the shock front may disappear locally, giving rise to what are called as shock holes. LIA does not predict shock holes and is therefore valid only in the wrinkled regime. The same is expected to be true for the weakly nonlinear framework that builds upon the LIA solution.
The criteria ![]() $M_t/(M_1-1) = 0.6$ given by Donzis (Reference Donzis2012b) is often used to demarcate the wrinkled and broken-shock regimes, where
$M_t/(M_1-1) = 0.6$ given by Donzis (Reference Donzis2012b) is often used to demarcate the wrinkled and broken-shock regimes, where ![]() $M_t$ is the turbulent Mach number that quantifies the intensity of the upstream turbulent fluctuations. It is related to the vorticity wave amplitude
$M_t$ is the turbulent Mach number that quantifies the intensity of the upstream turbulent fluctuations. It is related to the vorticity wave amplitude ![]() $\epsilon$ as
$\epsilon$ as ![]() $M_t = \epsilon M_1$. We restrict the range of
$M_t = \epsilon M_1$. We restrict the range of ![]() $\epsilon$ in our study to meet this criteria for wrinkled shock interaction. For the chosen range of Mach numbers between 1.25 and 2.0, this gives the maximum value of
$\epsilon$ in our study to meet this criteria for wrinkled shock interaction. For the chosen range of Mach numbers between 1.25 and 2.0, this gives the maximum value of ![]() $\epsilon$ to be between 0.12 and 0.3. We thus choose
$\epsilon$ to be between 0.12 and 0.3. We thus choose ![]() $\epsilon$ to vary between 0.01 and 0.25 to study the weakly nonlinear effects at the shock wave. As per (3.9), the normalized second-order vorticity
$\epsilon$ to vary between 0.01 and 0.25 to study the weakly nonlinear effects at the shock wave. As per (3.9), the normalized second-order vorticity ![]() $\varOmega _2^{(2)}$ is proportional to
$\varOmega _2^{(2)}$ is proportional to ![]() $\epsilon ^2 \phi$, where
$\epsilon ^2 \phi$, where ![]() $\phi$ is
$\phi$ is ![]() $O(1)$. The deviation of the numerical solution from LIA is therefore expected to have a magnitude
$O(1)$. The deviation of the numerical solution from LIA is therefore expected to have a magnitude ![]() $\epsilon ^2 \sim 0.06$ as can be observed from figure 12.
$\epsilon ^2 \sim 0.06$ as can be observed from figure 12.
The nonlinearity at the shock wave is also driven by inter-modal interaction, as noted in § 3. In the current study, the upstream disturbance field is purely vortical, while the downstream disturbances include vorticity, acoustic and entropy modes. As per the LIA, amplification across the shock is characterized by the transfer coefficients plotted in figure 2. We note the high values of ![]() $Z_{vv}$ and
$Z_{vv}$ and ![]() $Z_{vx}$ in the vicinity of the critical incidence
$Z_{vx}$ in the vicinity of the critical incidence ![]() $\alpha _c$, which can limit the applicability of LIA and the weakly nonlinear framework. The value of
$\alpha _c$, which can limit the applicability of LIA and the weakly nonlinear framework. The value of ![]() $\alpha _c$ is approximately
$\alpha _c$ is approximately ![]() $62^\circ$ for the range of Mach numbers considered here, and we restrict the range of
$62^\circ$ for the range of Mach numbers considered here, and we restrict the range of ![]() $\alpha$ to approximately
$\alpha$ to approximately ![]() $60^\circ$. The results for
$60^\circ$. The results for ![]() $\alpha = 20^\circ \unicode{x2013}40^\circ$ are presented in § 4.1, while the higher values of
$\alpha = 20^\circ \unicode{x2013}40^\circ$ are presented in § 4.1, while the higher values of ![]() $\alpha$ are discussed in § 5.
$\alpha$ are discussed in § 5.
We use the weakly nonlinear framework to explore second-order vorticity for Mach numbers up to 5. The LIA transfer coefficients are found to reach close to their asymptotic values in the hypersonic regime. The same is expected to hold for ![]() $\varOmega _2^{(2)}$. The comparison with numerical solution (§ 4.1) is limited to Mach 2, primarily owing to the limitations of the numerical methodology. The shock-grid misalignment error increases with shock strength, which makes it difficult to perform a meaningful comparison with the theoretical predictions. The same is true for incidence angles
$\varOmega _2^{(2)}$. The comparison with numerical solution (§ 4.1) is limited to Mach 2, primarily owing to the limitations of the numerical methodology. The shock-grid misalignment error increases with shock strength, which makes it difficult to perform a meaningful comparison with the theoretical predictions. The same is true for incidence angles ![]() $\alpha$ beyond
$\alpha$ beyond ![]() $40^\circ$ and in the decaying regime (
$40^\circ$ and in the decaying regime (![]() $\alpha > \alpha _c$).
$\alpha > \alpha _c$).
The Mach number range from 1.25 to 2.0 is important in many high-speed flow applications. The Mach number in a scramjet combustor is in this range, where shock-induced mixing is important for efficient combustion. Shock–boundary layer interactions in hypersonic intakes may have a higher Mach number at the boundary layer edge, but the shock waves are highly inclined to the flow. The shock-normal Mach number is much lower, often in the range of 1–2 for a free stream Mach number of 5 (Schulein Reference Schulein2006) and even as high as 13 (Pasha & Sinha Reference Pasha and Sinha2012). Also, experiments studying the shock–turbulence interaction in wind tunnels are conducted in the low supersonic range because it is difficult and expensive to conduct them at higher ![]() $M_1$.
$M_1$.
5. Predictions of WNLF
We use the weakly nonlinear framework presented in § 3 to derive a limit for the validity of LIA for a range of Mach numbers. The theory is also used to study the nonlinear effects in vorticity at high ![]() $M_1$ and
$M_1$ and ![]() $\alpha$ close to the critical angle (
$\alpha$ close to the critical angle (![]() $\alpha _c$).
$\alpha _c$).
5.1. LIA limit
The applicability of LIA is evaluated by comparing the magnitude of the LIA-predicted vorticity (![]() $\varOmega _2^{(1)}$) given by (3.7a) and that of the second-order effect (
$\varOmega _2^{(1)}$) given by (3.7a) and that of the second-order effect (![]() $\varOmega _2^{(2)}$) given by WNLF in (3.8). LIA is expected to be valid when
$\varOmega _2^{(2)}$) given by WNLF in (3.8). LIA is expected to be valid when
We have from (3.9), ![]() $\phi = {|\varOmega _2^{(2)}|}/{\epsilon ^2\bar {U}_1k}$. Let us define
$\phi = {|\varOmega _2^{(2)}|}/{\epsilon ^2\bar {U}_1k}$. Let us define ![]() $\psi$ as
$\psi$ as
We plot the ratio ![]() $\phi /\psi$ as a function of
$\phi /\psi$ as a function of ![]() $M_1$, for different
$M_1$, for different ![]() $\alpha$, in figure 19(a). As
$\alpha$, in figure 19(a). As ![]() $M_1$ is increased, for a given
$M_1$ is increased, for a given ![]() $\alpha$, we observe that the ratio at first increases, reaches a maximum value and then decreases to attain an asymptotic limit in the hypersonic range. This can be understood in terms of the variation of the linear and second-order vorticity with Mach number, as discussed below.
$\alpha$, we observe that the ratio at first increases, reaches a maximum value and then decreases to attain an asymptotic limit in the hypersonic range. This can be understood in terms of the variation of the linear and second-order vorticity with Mach number, as discussed below.

Figure 19. Nonlinear effects in vorticity amplification represented using (a) a relative measure ![]() $\phi /\psi$, (b) an absolute measure
$\phi /\psi$, (b) an absolute measure ![]() $\epsilon _{limit}$.
$\epsilon _{limit}$.
The ratio ![]() $\phi /\psi$ approaches zero in the limit
$\phi /\psi$ approaches zero in the limit ![]() $M_1 \to 1$, as
$M_1 \to 1$, as ![]() $\phi \to 0$ and
$\phi \to 0$ and ![]() $\psi \to 1$. This is because
$\psi \to 1$. This is because
in this limit. In other words, the vorticity amplitude remains unaltered across an infinitely weak shock, which results in a finite value of the downstream linear vorticity. By comparison, the second-order vorticity becomes negligible in magnitude in the sonic limit. This is because ![]() $u'_1 = u'_2$,
$u'_1 = u'_2$, ![]() $\varOmega '_1 = \varOmega '_2$ and
$\varOmega '_1 = \varOmega '_2$ and ![]() $\xi _t = \xi _y = 0$ for a vanishing shock wave. Thus, the contribution of
$\xi _t = \xi _y = 0$ for a vanishing shock wave. Thus, the contribution of ![]() $\varOmega _a$ in (3.8) drops out and there is no net turbulent transport in the case of an infinitely weak shock wave. The other terms
$\varOmega _a$ in (3.8) drops out and there is no net turbulent transport in the case of an infinitely weak shock wave. The other terms ![]() $\varOmega _b = \varOmega _c = 0$ by virtue of
$\varOmega _b = \varOmega _c = 0$ by virtue of ![]() $\xi _{yy} = 0$ and
$\xi _{yy} = 0$ and ![]() $r = 1$, respectively, which results in a vanishing value of the second-order vorticity in this limit.
$r = 1$, respectively, which results in a vanishing value of the second-order vorticity in this limit.
Using Taylor series expansion of ![]() $\phi$ and
$\phi$ and ![]() $\psi$ in the vicinity of the sonic point and retaining only the first-order term in Mach number, we can write
$\psi$ in the vicinity of the sonic point and retaining only the first-order term in Mach number, we can write
where ![]() $\phi ^\prime$ and
$\phi ^\prime$ and ![]() $\psi ^\prime$ represent the derivative with respect to Mach number of the corresponding function. The slope of the ratio
$\psi ^\prime$ represent the derivative with respect to Mach number of the corresponding function. The slope of the ratio ![]() $\phi /\psi$ in figure 19(a) is therefore determined by the derivative
$\phi /\psi$ in figure 19(a) is therefore determined by the derivative ![]() $\phi ^\prime$. For weak shocks, the second-order vorticity increases in magnitude with increasing Mach number (see figure 7). Thus, the derivative
$\phi ^\prime$. For weak shocks, the second-order vorticity increases in magnitude with increasing Mach number (see figure 7). Thus, the derivative ![]() $\phi ^\prime$ is positive, and it increases with
$\phi ^\prime$ is positive, and it increases with ![]() $\alpha$ in the propagating regime. However, the initial slope of
$\alpha$ in the propagating regime. However, the initial slope of ![]() $\psi$ at
$\psi$ at ![]() $M_1 = 1$ is independent of Mach number, as
$M_1 = 1$ is independent of Mach number, as
and
The limiting slopes ![]() $\phi ^\prime$ and
$\phi ^\prime$ and ![]() $\psi ^\prime$ are plotted as a function of
$\psi ^\prime$ are plotted as a function of ![]() $\alpha$ in figure 20. Together, they give an increasing trend for the ratio
$\alpha$ in figure 20. Together, they give an increasing trend for the ratio ![]() $\phi /\psi$ for Mach numbers close to 1. However, although both
$\phi /\psi$ for Mach numbers close to 1. However, although both ![]() $\varOmega _2^{(2)}$ and
$\varOmega _2^{(2)}$ and ![]() $\varOmega _2^{(1)}$ reach asymptotic values in the large
$\varOmega _2^{(1)}$ reach asymptotic values in the large ![]() $M_1$ limit, the growth of
$M_1$ limit, the growth of ![]() $\varOmega _2^{(2)}$ becomes smaller as
$\varOmega _2^{(2)}$ becomes smaller as ![]() $M_1$ increases and reaches an asymptotic limit for smaller
$M_1$ increases and reaches an asymptotic limit for smaller ![]() $M_1$ when compared with
$M_1$ when compared with ![]() $\varOmega _2^{(1)}$ (see figures 6 and 7 which plot
$\varOmega _2^{(1)}$ (see figures 6 and 7 which plot ![]() $\phi$ and
$\phi$ and ![]() $\psi$). This results in a decreasing trend for
$\psi$). This results in a decreasing trend for ![]() $\phi /\psi$ for Mach numbers beyond 2, as is observed in figure 19(a). In the large
$\phi /\psi$ for Mach numbers beyond 2, as is observed in figure 19(a). In the large ![]() $M_1$ limit, this ratio reaches an asymptotic value that depends only on
$M_1$ limit, this ratio reaches an asymptotic value that depends only on ![]() $\alpha$. Thus, we get a local peak in
$\alpha$. Thus, we get a local peak in ![]() $\phi /\psi$, which corresponds to the Mach number, where the second-order effects are the largest compared with the first-order vorticity amplification, once the amplitude factors are scaled out.
$\phi /\psi$, which corresponds to the Mach number, where the second-order effects are the largest compared with the first-order vorticity amplification, once the amplitude factors are scaled out.

Figure 20. The slope of ![]() $\phi$ and
$\phi$ and ![]() $\psi$ in the limit of
$\psi$ in the limit of ![]() $M_1 \to 1$ as a function of incidence angle
$M_1 \to 1$ as a function of incidence angle ![]() $\alpha$.
$\alpha$.
The ratio ![]() $\phi /\psi$ is also observed to increase with the incidence angle
$\phi /\psi$ is also observed to increase with the incidence angle ![]() $\alpha$ (not shown). This behaviour in the low-Mach-number regime is in line with the results presented in figure 12 of § 4, whereas the variation for large Mach numbers is predicted using the weakly nonlinear framework presented in § 3. In short, the LIA prediction of vorticity amplification increases with
$\alpha$ (not shown). This behaviour in the low-Mach-number regime is in line with the results presented in figure 12 of § 4, whereas the variation for large Mach numbers is predicted using the weakly nonlinear framework presented in § 3. In short, the LIA prediction of vorticity amplification increases with ![]() $\alpha$, as per the variation of
$\alpha$, as per the variation of ![]() $Z_{vv}$ shown in figure 2(a). In comparison,
$Z_{vv}$ shown in figure 2(a). In comparison, ![]() $\varOmega _2^{(2)}$ varies as the product of two transfer coefficients, such as
$\varOmega _2^{(2)}$ varies as the product of two transfer coefficients, such as ![]() $Z_{vv}Z_{vp}$ or
$Z_{vv}Z_{vp}$ or ![]() $Z_{vv}Z_{vv}$ (as per (3.7b)) resulting in the observed trend in figure 2(a).
$Z_{vv}Z_{vv}$ (as per (3.7b)) resulting in the observed trend in figure 2(a).
Next, we rewrite (5.1) in terms of the functions ![]() $\phi$ and
$\phi$ and ![]() $\psi$ to arrive at a limit on
$\psi$ to arrive at a limit on ![]() $\epsilon$ for LIA to be valid,
$\epsilon$ for LIA to be valid,
Here, a factor of 0.1 is introduced to change the inequality to equality under the assumption that the second-order vorticity is less than or equal to ![]() $10\,\%$ of the linear vorticity in magnitude. This corresponds to a maximum of
$10\,\%$ of the linear vorticity in magnitude. This corresponds to a maximum of ![]() $10\,\%$ error in LIA results.
$10\,\%$ error in LIA results.
Figure 19(b) shows the variation of ![]() $\epsilon _{limit}$ with
$\epsilon _{limit}$ with ![]() $M_1$ for various
$M_1$ for various ![]() $\alpha$ values evaluated using (5.7). As expected, the variation of
$\alpha$ values evaluated using (5.7). As expected, the variation of ![]() $\epsilon _{limit}$ with
$\epsilon _{limit}$ with ![]() $M_1$ at a given
$M_1$ at a given ![]() $\alpha$ is non-monotonic. It decreases with increasing
$\alpha$ is non-monotonic. It decreases with increasing ![]() $M_1$ for weak shocks, reaches a local minima and subsequently increases for higher Mach numbers. It is opposite to the trend observed in figure 19(a), where the ratio
$M_1$ for weak shocks, reaches a local minima and subsequently increases for higher Mach numbers. It is opposite to the trend observed in figure 19(a), where the ratio ![]() $\phi /\psi$ gives the relative measure of nonlinearity in vorticity. However, figure 19(b) provides an absolute quantitative limit on the upstream vorticity wave amplitude as a function of flow parameters. At a given
$\phi /\psi$ gives the relative measure of nonlinearity in vorticity. However, figure 19(b) provides an absolute quantitative limit on the upstream vorticity wave amplitude as a function of flow parameters. At a given ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$,
$M_1$, ![]() $\epsilon$ values above
$\epsilon$ values above ![]() $\epsilon _{limit}$ would breach the limit of LIA validity, which results in the prediction that have more than
$\epsilon _{limit}$ would breach the limit of LIA validity, which results in the prediction that have more than ![]() $10\,\%$ error.
$10\,\%$ error.
The minimum value of ![]() $\epsilon _{limit}$ is attained at
$\epsilon _{limit}$ is attained at ![]() $M_1 \simeq 2$ for the different
$M_1 \simeq 2$ for the different ![]() $\alpha$ values shown in figure 19(b). This poses the strictest limit on the range of upstream vorticity magnitude
$\alpha$ values shown in figure 19(b). This poses the strictest limit on the range of upstream vorticity magnitude ![]() $\epsilon$ for which LIA results are accurate. At lower Mach numbers (
$\epsilon$ for which LIA results are accurate. At lower Mach numbers (![]() $M_1 < 2$), higher values of
$M_1 < 2$), higher values of ![]() $\epsilon$ are permissible. In fact, the
$\epsilon$ are permissible. In fact, the ![]() $\epsilon _{limit}$ curves have a singular behaviour at
$\epsilon _{limit}$ curves have a singular behaviour at ![]() $M_1 = 1$. This can be resolved by noting the limiting behaviour of the first-order vorticity and the second-order vorticity given in (5.3).
$M_1 = 1$. This can be resolved by noting the limiting behaviour of the first-order vorticity and the second-order vorticity given in (5.3).
As noted above, ![]() $\epsilon _{limit}$ increases with Mach number for
$\epsilon _{limit}$ increases with Mach number for ![]() $M_1 > 2$, which implies that LIA is valid for a larger range of
$M_1 > 2$, which implies that LIA is valid for a larger range of ![]() $\epsilon$ at higher Mach numbers, or equivalently, for stronger shock waves. The mean compression of the shock amplifies vorticity disturbances in the flow and this linear effect is accurately predicted by LIA. A stronger shock leads to a higher amplification of vorticity amplitude. However, the second-order vorticity is generated by nonlinear effects owing to the inter-modal interaction and shock-curvature effects, as per the weakly nonlinear framework. The amplitude of the downstream Kovásznay modes and the shock oscillation both depend on the disturbance level upstream of the shock. The
$\epsilon$ at higher Mach numbers, or equivalently, for stronger shock waves. The mean compression of the shock amplifies vorticity disturbances in the flow and this linear effect is accurately predicted by LIA. A stronger shock leads to a higher amplification of vorticity amplitude. However, the second-order vorticity is generated by nonlinear effects owing to the inter-modal interaction and shock-curvature effects, as per the weakly nonlinear framework. The amplitude of the downstream Kovásznay modes and the shock oscillation both depend on the disturbance level upstream of the shock. The ![]() $\epsilon _{limit}$ in figure 19(b) can thus be interpreted as a balance between two competing effects. A stronger shock favours the linear effect owing to the mean compression of the shock, while larger amplitude disturbance (higher
$\epsilon _{limit}$ in figure 19(b) can thus be interpreted as a balance between two competing effects. A stronger shock favours the linear effect owing to the mean compression of the shock, while larger amplitude disturbance (higher ![]() $\epsilon$) increases the nonlinear contribution. For a given Mach number, the value of
$\epsilon$) increases the nonlinear contribution. For a given Mach number, the value of ![]() $\epsilon _{limit}$ is a function of the vorticity wave incidence angle. For the different values of
$\epsilon _{limit}$ is a function of the vorticity wave incidence angle. For the different values of ![]() $\alpha$ presented in figure 19(b),
$\alpha$ presented in figure 19(b), ![]() $\epsilon _{limit}$ increases monotonically at higher Mach numbers, which indicates that LIA has a higher range of validity for strong shock waves.
$\epsilon _{limit}$ increases monotonically at higher Mach numbers, which indicates that LIA has a higher range of validity for strong shock waves.
The validity of LIA for the shock–turbulence interaction is usually prescribed in terms of ![]() $M_t$ and
$M_t$ and ![]() $M_1$. For example, the criteria
$M_1$. For example, the criteria ![]() $M_t/(M_1-1) = 0.6$ is frequently used to demarcate the wrinkled regime and broken shock interactions (Donzis Reference Donzis2012b). The
$M_t/(M_1-1) = 0.6$ is frequently used to demarcate the wrinkled regime and broken shock interactions (Donzis Reference Donzis2012b). The ![]() $\epsilon _{limit}$ presented above can be interpreted in a similar vein by noting that
$\epsilon _{limit}$ presented above can be interpreted in a similar vein by noting that ![]() $\epsilon = M_t/M_1$, such that the values plotted in figure 19(b) give an upper limit on the ratio of
$\epsilon = M_t/M_1$, such that the values plotted in figure 19(b) give an upper limit on the ratio of ![]() $M_t$ to
$M_t$ to ![]() $M_1$ for the validity of LIA for the shock–vorticity wave interaction. As per the weakly nonlinear framework, this limit is a function of the incidence angle and shock strength. For a given Mach number, (5.7) can be integrated over all possible
$M_1$ for the validity of LIA for the shock–vorticity wave interaction. As per the weakly nonlinear framework, this limit is a function of the incidence angle and shock strength. For a given Mach number, (5.7) can be integrated over all possible ![]() $\alpha$ (in three-dimensional space) to get an estimate of
$\alpha$ (in three-dimensional space) to get an estimate of ![]() $\epsilon _{limit}$ for the shock–turbulence interaction. Further, the limit is derived based on the magnitude of the second-order vorticity. It may be different if we consider nonlinear effects in other quantities like Reynolds stresses and downstream pressure fluctuations. The weakly nonlinear framework can be extended to study other quantities of interest to get a more general criterion for the validity of LIA.
$\epsilon _{limit}$ for the shock–turbulence interaction. Further, the limit is derived based on the magnitude of the second-order vorticity. It may be different if we consider nonlinear effects in other quantities like Reynolds stresses and downstream pressure fluctuations. The weakly nonlinear framework can be extended to study other quantities of interest to get a more general criterion for the validity of LIA.
5.2. Second-order effects at high  $M_1$ and
$M_1$ and  $\alpha$
$\alpha$
We use the expressions derived in § 3 to analyse the nonlinear effects in vorticity amplification for high ![]() $\alpha$ and
$\alpha$ and ![]() $M_1$ regime to understand the underlying physics better. Figure 21 shows that the second-order vorticity increases with Mach number (
$M_1$ regime to understand the underlying physics better. Figure 21 shows that the second-order vorticity increases with Mach number (![]() $M_1$) and reaches an asymptotic value in the hypersonic limit. However,
$M_1$) and reaches an asymptotic value in the hypersonic limit. However, ![]() $\phi$ exhibits a sharp increase near
$\phi$ exhibits a sharp increase near ![]() $\alpha _c$, by approximately a factor of 10 compared with its value at
$\alpha _c$, by approximately a factor of 10 compared with its value at ![]() $\alpha = 30^\circ$ considered in § 4.
$\alpha = 30^\circ$ considered in § 4.

Figure 21. Variation of ![]() $\varOmega _2^{(2)}$ from (3.8) (circle),
$\varOmega _2^{(2)}$ from (3.8) (circle), ![]() $\varOmega _a+\varOmega _b$ (dashed line) and
$\varOmega _a+\varOmega _b$ (dashed line) and ![]() $\varOmega _a+\varOmega _b+\varOmega _c$ (triangle) with (a)
$\varOmega _a+\varOmega _b+\varOmega _c$ (triangle) with (a) ![]() $M_1$ at
$M_1$ at ![]() $\alpha =60^\circ$, (b)
$\alpha =60^\circ$, (b) ![]() $\alpha$ at
$\alpha$ at ![]() $M_1=3$.
$M_1=3$.
Figure 22 plots the variation of the constituent terms ![]() $\varOmega _a$,
$\varOmega _a$, ![]() $\varOmega _b$ and
$\varOmega _b$ and ![]() $\varOmega _c$ of the second-order vorticity as a function of
$\varOmega _c$ of the second-order vorticity as a function of ![]() $M_1$ and
$M_1$ and ![]() $\alpha$. At low values of
$\alpha$. At low values of ![]() $\alpha$ (see figure 22a), the second-order vorticity is dominated by the turbulent transport term
$\alpha$ (see figure 22a), the second-order vorticity is dominated by the turbulent transport term ![]() $\varOmega _a$ and the shock-curvature effect
$\varOmega _a$ and the shock-curvature effect ![]() $\varOmega _b$. The
$\varOmega _b$. The ![]() $\varOmega _c$ term is comparatively small in magnitude and was neglected in the analysis presented earlier. The
$\varOmega _c$ term is comparatively small in magnitude and was neglected in the analysis presented earlier. The ![]() $\varOmega _c$ constitutes the additional effect of the turbulent flux of vorticity and shock-curvature along with dilatation, which becomes significant at
$\varOmega _c$ constitutes the additional effect of the turbulent flux of vorticity and shock-curvature along with dilatation, which becomes significant at ![]() $\alpha$ close to
$\alpha$ close to ![]() $\alpha _c$. The nonlinear effects at
$\alpha _c$. The nonlinear effects at ![]() $\alpha$ close to
$\alpha$ close to ![]() $\alpha _c$ is dominated by
$\alpha _c$ is dominated by ![]() $\varOmega _b$ (see figure 22b). The other parts,
$\varOmega _b$ (see figure 22b). The other parts, ![]() $\varOmega _a$ and
$\varOmega _a$ and ![]() $\varOmega _c$, have a non-negligible contribution to second-order vorticity at such high
$\varOmega _c$, have a non-negligible contribution to second-order vorticity at such high ![]() $\alpha$. The dramatic rise in
$\alpha$. The dramatic rise in ![]() $\varOmega _b$ for high incidence angles is also visible in figures 22(c) and 22(d), which plot the variation of the constituent terms at
$\varOmega _b$ for high incidence angles is also visible in figures 22(c) and 22(d), which plot the variation of the constituent terms at ![]() $M_1 = 1.75$ and
$M_1 = 1.75$ and ![]() $5$, respectively.
$5$, respectively.

Figure 22. Variation of the magnitude of ![]() $\varOmega _a$ (circle),
$\varOmega _a$ (circle), ![]() $\varOmega _b$ (triangle) and
$\varOmega _b$ (triangle) and ![]() $\varOmega _c$ (square) from (3.8) with
$\varOmega _c$ (square) from (3.8) with ![]() $M_1$: (a) at
$M_1$: (a) at ![]() $\alpha =30^\circ$; (b) at
$\alpha =30^\circ$; (b) at ![]() $\alpha =60^\circ$ and with
$\alpha =60^\circ$ and with ![]() $\alpha$ (c) at
$\alpha$ (c) at ![]() $M_1=1.75$; (d) at
$M_1=1.75$; (d) at ![]() $M_1= 5$.
$M_1= 5$.
The variation of ![]() $\varOmega ^{(2)}_2$ and its constituent terms at high
$\varOmega ^{(2)}_2$ and its constituent terms at high ![]() $\alpha$ can be interpreted in terms of the transfer coefficients presented in figure 2(a). Both
$\alpha$ can be interpreted in terms of the transfer coefficients presented in figure 2(a). Both ![]() $Z_{vv}$ and
$Z_{vv}$ and ![]() $Z_{vx}$ show a sharp rise in the vicinity of the critical angle and all the transfer coefficients, including
$Z_{vx}$ show a sharp rise in the vicinity of the critical angle and all the transfer coefficients, including ![]() $Z_{vp}$, have singular behaviour at
$Z_{vp}$, have singular behaviour at ![]() $\alpha _c$. The resulting intermodal interaction terms in (3.10) and (3.11) also show a similar behaviour, and this would severely restrict the validity of LIA at the critical angle.
$\alpha _c$. The resulting intermodal interaction terms in (3.10) and (3.11) also show a similar behaviour, and this would severely restrict the validity of LIA at the critical angle.
6. Summary and conclusions
In this paper, we present a weakly nonlinear framework for the interaction of two-dimensional vorticity waves with a normal shock. The shock–vorticity interaction is one of the elementary problems that form the basis of linear interaction analysis to study the shock–turbulence interaction. The weakly nonlinear framework presented is based on the inviscid and ideal gas assumptions, where the shock is assumed to be a discontinuity. The nominally normal shock wave distorts and oscillates about its mean position in response to the unsteady fluctuations passing through it. We study second-order effects at the shock wave to identify the physical mechanisms responsible for nonlinear amplification of vorticity across the shock. A range of shock Mach numbers (![]() $M_1$), vorticity wave amplitudes (
$M_1$), vorticity wave amplitudes (![]() $\epsilon$) and incidence angles (
$\epsilon$) and incidence angles (![]() $\alpha$) up to the critical angle are considered.
$\alpha$) up to the critical angle are considered.
It is found that the second-order amplification of vorticity increases with the incidence angle of the vorticity wave to reach a singularity at the critical angle. The variation with ![]() $M_1$ is non-monotonic, with a rapid rise at low
$M_1$ is non-monotonic, with a rapid rise at low ![]() $M_1$ to reach an asymptotic value in the hypersonic limit. The analysis predicts that the generation of second-order vorticity at the shock wave is primarily owing to shock curvature and turbulent transport of vorticity. The turbulent transport has a significant contribution from intermodal interaction between the vorticity and acoustic waves generated at the shock, and it is dominant at low
$M_1$ to reach an asymptotic value in the hypersonic limit. The analysis predicts that the generation of second-order vorticity at the shock wave is primarily owing to shock curvature and turbulent transport of vorticity. The turbulent transport has a significant contribution from intermodal interaction between the vorticity and acoustic waves generated at the shock, and it is dominant at low ![]() $\alpha$ and low
$\alpha$ and low ![]() $M_1$ except close to the sonic limit. However, the shock curvature plays a vital role in vorticity amplification at high
$M_1$ except close to the sonic limit. However, the shock curvature plays a vital role in vorticity amplification at high ![]() $\alpha$ close to the critical value.
$\alpha$ close to the critical value.
We use a high-order accurate numerical method to compute the shock–vorticity interaction for a range of ![]() $M_1$,
$M_1$, ![]() $\epsilon$ and
$\epsilon$ and ![]() $\alpha$. The simulations employ a fifth-order WENO method in the region of the shock wave and a sixth-order central difference scheme in the rest of the domain. The deviation of the numerical solution from LIA prediction, denoted by
$\alpha$. The simulations employ a fifth-order WENO method in the region of the shock wave and a sixth-order central difference scheme in the rest of the domain. The deviation of the numerical solution from LIA prediction, denoted by ![]() $\sigma _N$, is quantified and compared with predictions of the weakly nonlinear framework. It is found that
$\sigma _N$, is quantified and compared with predictions of the weakly nonlinear framework. It is found that ![]() $\sigma _N$ has a second-order variation with
$\sigma _N$ has a second-order variation with ![]() $\epsilon$ and this is in line with the second-order vorticity magnitude obtained analytically. The
$\epsilon$ and this is in line with the second-order vorticity magnitude obtained analytically. The ![]() $\sigma _N$ value also increases with
$\sigma _N$ value also increases with ![]() $M_1$ and
$M_1$ and ![]() $\alpha$, matching the trend in the weakly nonlinear framework. Further, the theoretical predictions are able to collapse the numerical data over the range of both Mach number and
$\alpha$, matching the trend in the weakly nonlinear framework. Further, the theoretical predictions are able to collapse the numerical data over the range of both Mach number and ![]() $\alpha$ tested in the simulations. Thus the weakly nonlinear framework is a valuable addition to LIA that is widely used to study the shock–turbulence interaction.
$\alpha$ tested in the simulations. Thus the weakly nonlinear framework is a valuable addition to LIA that is widely used to study the shock–turbulence interaction.
An important additional contribution of the present framework is to predict a limit to the validity of LIA. We compare the magnitude of vorticity amplification predicted by LIA with the second-order vorticity obtained from the weakly nonlinear analysis. The results are presented in the form of an upper bound to the vorticity wave amplitude, for which the error caused by neglecting higher-order terms is less than ![]() $10\,\%$. The limiting
$10\,\%$. The limiting ![]() $\epsilon$ value is found to be high for the
$\epsilon$ value is found to be high for the ![]() $M_1 \to 1$ and
$M_1 \to 1$ and ![]() $M_1 \to \infty$ limit, with local minima near
$M_1 \to \infty$ limit, with local minima near ![]() $M_1 = 2$ for
$M_1 = 2$ for ![]() $\gamma =1.4$. This implies that LIA is most restrictive at this
$\gamma =1.4$. This implies that LIA is most restrictive at this ![]() $M_1$, with a higher
$M_1$, with a higher ![]() $\epsilon$ range of applicability at higher and lower Mach numbers.
$\epsilon$ range of applicability at higher and lower Mach numbers.
The analysis presented in this work provides a template to study nonlinear effects in more general interactions such as a vortex passing through a shock and the shock–turbulence interaction. The analysis can also be extended to other kinds of upstream disturbances, namely, acoustic waves, entropy waves or their combinations. For a given fundamental mode, its interaction with other modes is governed by the underlying transfer coefficients. For the prediction of nonlinear effects in downstream vorticity in the range studied, we find that the interaction of the vorticity mode with the acoustic mode is most dominant.
The framework exhibited in this paper considers the nonlinear effects arising from the interaction of a pure vorticity wave with a normal shock in an ideal gas. If we consider fluctuations of thermodynamic quantities upstream of the shock, equations need to be adjusted accordingly. This framework is valid specifically in a weakly nonlinear regime where the amplitude of upstream fluctuations is not too large to distort the shock structure significantly. Moreover, the weakly nonlinear framework presented here is valid only at the shock. Further investigation is needed to study the effects of modal interaction downstream of the shock.
Acknowledgements
We thank Prof J. Larsson, University of Maryland, College Park, MD, for providing the code to perform numerical computations presented in this study.
Declaration of interests
The authors report no conflict of interest.
Appendix A
Higher-order effects in vorticity are given by (3.7b). We derive ![]() $\varOmega _a$,
$\varOmega _a$, ![]() $\varOmega _b$ and
$\varOmega _b$ and ![]() $\varOmega _c$ given in (3.8) as follows. We have
$\varOmega _c$ given in (3.8) as follows. We have
 \begin{align} \varOmega_2^{(2)}&= \frac{(u_1'-\xi_t)}{\bar{U}_2}\frac{\partial v_1'}{\partial x} -\frac{(u_2'-\xi_t)}{\bar{U}_2}\frac{\partial v_2'}{\partial x}- \frac{\partial}{\partial y}\left[\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right] + \frac{v_1'}{\bar{U}_2}\frac{\partial v_1'}{\partial y}\nonumber\\ &\quad -\frac{v_2'}{\bar{U}_2}\frac{\partial v_2'}{\partial y}-\frac{\partial \xi_y(v_2'-v_1')}{\partial y}+ \frac{\partial}{\partial y} \frac{\rho_2'(u_2'-\xi_t)}{\bar{\rho}_2} + \frac{\rho_2'}{\bar{U}_2\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y}. \end{align}
\begin{align} \varOmega_2^{(2)}&= \frac{(u_1'-\xi_t)}{\bar{U}_2}\frac{\partial v_1'}{\partial x} -\frac{(u_2'-\xi_t)}{\bar{U}_2}\frac{\partial v_2'}{\partial x}- \frac{\partial}{\partial y}\left[\frac{(u_1'-\xi_t)^2}{2\bar{U}_1} - \frac{(u_2'-\xi_t)^2}{2\bar{U}_2}\right] + \frac{v_1'}{\bar{U}_2}\frac{\partial v_1'}{\partial y}\nonumber\\ &\quad -\frac{v_2'}{\bar{U}_2}\frac{\partial v_2'}{\partial y}-\frac{\partial \xi_y(v_2'-v_1')}{\partial y}+ \frac{\partial}{\partial y} \frac{\rho_2'(u_2'-\xi_t)}{\bar{\rho}_2} + \frac{\rho_2'}{\bar{U}_2\bar{\rho}_2^2}\frac{\partial p_2'}{\partial y}. \end{align}The terms corresponding to shock-unsteadiness, baroclinic torque and the effect of the fluctuations in mass flux are found to be negligible. Therefore, simplifying and rearranging (A1) gives
 \begin{align} \varOmega_2^{(2)} &\approx\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2} + \frac{v_1'+\bar{U}_1\xi_y}{\bar{U}_2}\frac{\partial v_1'}{\partial y}-\frac{v_2'+\bar{U}_2\xi_y}{\bar{U}_2} \frac{\partial v_2'}{\partial y} \nonumber\\ &\quad + \frac{(u_1'-u_2')}{\bar{U}_2}\frac{\partial \xi_t}{\partial y}+\frac{b(u_1'-\xi_t)}{\bar{U}_2} \frac{\partial (u_1'-\xi_t)}{\partial y}-(v_2'-v_1')\xi_{yy}+(1-r)\xi_y\frac{\partial v_1'}{\partial y},\end{align}
\begin{align} \varOmega_2^{(2)} &\approx\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2} + \frac{v_1'+\bar{U}_1\xi_y}{\bar{U}_2}\frac{\partial v_1'}{\partial y}-\frac{v_2'+\bar{U}_2\xi_y}{\bar{U}_2} \frac{\partial v_2'}{\partial y} \nonumber\\ &\quad + \frac{(u_1'-u_2')}{\bar{U}_2}\frac{\partial \xi_t}{\partial y}+\frac{b(u_1'-\xi_t)}{\bar{U}_2} \frac{\partial (u_1'-\xi_t)}{\partial y}-(v_2'-v_1')\xi_{yy}+(1-r)\xi_y\frac{\partial v_1'}{\partial y},\end{align} \begin{align} &\approx\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2} + [\cot\alpha (u_1'-u_2')+(1-r)v_1'+(\bar{U}_2-r\bar{U}_1)\xi_y]\xi_{yy}\nonumber\\ &\quad +(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -\left(\frac{r+1}{r-1}\right) \cot\alpha(u_1'-u_2')\xi_{yy}\right], \end{align}
\begin{align} &\approx\frac{(u_1'-\xi_t) \varOmega_1'-(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2} + [\cot\alpha (u_1'-u_2')+(1-r)v_1'+(\bar{U}_2-r\bar{U}_1)\xi_y]\xi_{yy}\nonumber\\ &\quad +(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -\left(\frac{r+1}{r-1}\right) \cot\alpha(u_1'-u_2')\xi_{yy}\right], \end{align} \begin{align} &\approx \underbrace{\frac{r(u_1'-\xi_t) \varOmega_1'}{\bar{U}_1}- \frac{(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2}}_{\varOmega_a} +\underbrace{[{-}r(v_1'+\bar{U}_1\xi_y )+(-\cot\alpha u_2'+\bar{U}_2\xi_y)]\xi_{yy}}_{\varOmega_b}\nonumber\\ &\quad +\underbrace{(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -c_d\cot\alpha(u_1'-u_2')\xi_{yy}\right]}_{\varOmega_c}, \end{align}
\begin{align} &\approx \underbrace{\frac{r(u_1'-\xi_t) \varOmega_1'}{\bar{U}_1}- \frac{(u_2'-\xi_t)\varOmega_2'}{\bar{U}_2}}_{\varOmega_a} +\underbrace{[{-}r(v_1'+\bar{U}_1\xi_y )+(-\cot\alpha u_2'+\bar{U}_2\xi_y)]\xi_{yy}}_{\varOmega_b}\nonumber\\ &\quad +\underbrace{(r-1)\left[\frac{\partial }{\partial y}\frac{(u_1'-\xi_t)^2}{2\bar{U}_1}-\xi_y \frac{\partial v_1'}{\partial y} -c_d\cot\alpha(u_1'-u_2')\xi_{yy}\right]}_{\varOmega_c}, \end{align}
where ![]() $c_d={(r+1)}/{(r-1)}$. Thus we have for second-order vorticity fluctuations
$c_d={(r+1)}/{(r-1)}$. Thus we have for second-order vorticity fluctuations