Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hadid, L. Z.
Sahraoui, F.
Kiyani, K. H.
Retinò, A.
Modolo, R.
Canu, P.
Masters, A.
and
Dougherty, M. K.
2015.
NATURE OF THE MHD AND KINETIC SCALE TURBULENCE IN THE MAGNETOSHEATH OF SATURN:
CASSINI
OBSERVATIONS
.
The Astrophysical Journal,
Vol. 813,
Issue. 2,
p.
L29.
Howes, G. G.
2015.
A dynamical model of plasma turbulence in the solar wind.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 373,
Issue. 2041,
p.
20140145.
Clark di Leoni, P.
Cobelli, P. J.
and
Mininni, P. D.
2015.
The spatio-temporal spectrum of turbulent flows.
The European Physical Journal E,
Vol. 38,
Issue. 12,
Oughton, S.
Matthaeus, W. H.
Wan, M.
and
Osman, K. T.
2015.
Anisotropy in solar wind plasma turbulence.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 373,
Issue. 2041,
p.
20140152.
Chibbaro, Sergio
and
Josserand, Christophe
2016.
Elastic wave turbulence and intermittency.
Physical Review E,
Vol. 94,
Issue. 1,
Meyrand, Romain
Galtier, Sébastien
and
Kiyani, Khurom H.
2016.
Direct Evidence of the Transition from Weak to Strong Magnetohydrodynamic Turbulence.
Physical Review Letters,
Vol. 116,
Issue. 10,
Banerjee, Supratik
and
Galtier, Sébastien
2016.
Chiral exact relations for helicities in Hall magnetohydrodynamic turbulence.
Physical Review E,
Vol. 93,
Issue. 3,
Lugones, R.
Dmitruk, P.
Mininni, P. D.
Wan, M.
and
Matthaeus, W. H.
2016.
On the spatio-temporal behavior of magnetohydrodynamic turbulence in a magnetized plasma.
Physics of Plasmas,
Vol. 23,
Issue. 11,
Andrés, N.
Clark di Leoni, P.
Mininni, P. D.
Dmitruk, P.
Sahraoui, F.
and
Matthaeus, W. H.
2017.
Interplay between Alfvén and magnetosonic waves in compressible magnetohydrodynamics turbulence.
Physics of Plasmas,
Vol. 24,
Issue. 10,
Chibbaro, S.
De Lillo, F.
and
Onorato, M.
2017.
Weak versus strong wave turbulence in the Majda-McLaughlin-Tabak model.
Physical Review Fluids,
Vol. 2,
Issue. 5,
Chandran, Benjamin D. G.
2018.
Parametric instability, inverse cascade and the range of solar-wind turbulence.
Journal of Plasma Physics,
Vol. 84,
Issue. 1,
Meyrand, Romain
Kiyani, Khurom H.
Gürcan, Özgur D.
and
Galtier, Sébastien
2018.
Coexistence of Weak and Strong Wave Turbulence in Incompressible Hall Magnetohydrodynamics.
Physical Review X,
Vol. 8,
Issue. 3,
Bell, N K
and
Nazarenko, S V
2018.
Reflected wave solution of Alfvén wave turbulence.
Journal of Physics A: Mathematical and Theoretical,
Vol. 51,
Issue. 40,
p.
405501.
Offermans, Gerardus Petrus
Biferale, Luca
Buzzicotti, Michele
and
Linkmann, Moritz
2018.
A priori study of the subgrid energy transfers for small-scale dynamo in kinematic and saturation regimes.
Physics of Plasmas,
Vol. 25,
Issue. 12,
Chibbaro, Sergio
Dematteis, Giovanni
and
Rondoni, Lamberto
2018.
4-wave dynamics in kinetic wave turbulence.
Physica D: Nonlinear Phenomena,
Vol. 362,
Issue. ,
p.
24.
Passot, T.
and
Sulem, P. L.
2019.
Imbalanced kinetic Alfvén wave turbulence: from weak turbulence theory to nonlinear diffusion models for the strong regime.
Journal of Plasma Physics,
Vol. 85,
Issue. 03,
Lugones, R.
Dmitruk, P.
Mininni, P. D.
Pouquet, A.
and
Matthaeus, W. H.
2019.
Spatio-temporal behavior of magnetohydrodynamic fluctuations with cross-helicity and background magnetic field.
Physics of Plasmas,
Vol. 26,
Issue. 12,
Pouquet, A.
Rosenberg, D.
Stawarz, J.E.
and
Marino, R.
2019.
Helicity Dynamics, Inverse, and Bidirectional Cascades in Fluid and Magnetohydrodynamic Turbulence: A Brief Review.
Earth and Space Science,
Vol. 6,
Issue. 3,
p.
351.
Chandran, Benjamin D. G.
and
Perez, Jean C.
2019.
Reflection-driven magnetohydrodynamic turbulence in the solar atmosphere and solar wind.
Journal of Plasma Physics,
Vol. 85,
Issue. 4,
Pouquet, Annick
Rosenberg, Duane
and
Stawarz, Julia E.
2020.
Interplay between turbulence and waves: large-scale helical transfer, and small-scale dissipation and mixing in fluid and Hall-MHD turbulence.
Rendiconti Lincei. Scienze Fisiche e Naturali,
Vol. 31,
Issue. 4,
p.
949.
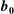 $\boldsymbol{b}_{\mathbf{0}}$ and zero cross-helicity. At leading order, this asymptotic regime is achieved via three-wave resonant interactions with the scattering of a wave on a 2D mode for which
$\boldsymbol{b}_{\mathbf{0}}$ and zero cross-helicity. At leading order, this asymptotic regime is achieved via three-wave resonant interactions with the scattering of a wave on a 2D mode for which 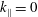 $k_{\Vert }=0$. When the interactions with the 2D modes are artificially reduced, we show numerically that the system exhibits an energy spectrum with
$k_{\Vert }=0$. When the interactions with the 2D modes are artificially reduced, we show numerically that the system exhibits an energy spectrum with 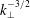 $k_{\bot }^{-3/2}$, whereas the expected exact solution with
$k_{\bot }^{-3/2}$, whereas the expected exact solution with 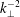 $k_{\bot }^{-2}$ is recovered with the full nonlinear system. In the latter case, strong intermittency is found when the vector separation of structure functions is taken transverse to
$k_{\bot }^{-2}$ is recovered with the full nonlinear system. In the latter case, strong intermittency is found when the vector separation of structure functions is taken transverse to 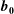 $\boldsymbol{b}_{\mathbf{0}}$. This result may be explained by the influence of the 2D modes whose regime belongs to strong turbulence. In addition to shedding light on the origin of this intermittency, we derive a log-Poisson law,
$\boldsymbol{b}_{\mathbf{0}}$. This result may be explained by the influence of the 2D modes whose regime belongs to strong turbulence. In addition to shedding light on the origin of this intermittency, we derive a log-Poisson law, 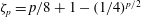 ${\it\zeta}_{p}=p/8+1-(1/4)^{p/2}$, which fits the data perfectly and highlights the important role of parallel current sheets.
${\it\zeta}_{p}=p/8+1-(1/4)^{p/2}$, which fits the data perfectly and highlights the important role of parallel current sheets.