Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T21:42:59.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Wavy regime of a power-law film flow

Published online by Cambridge University Press:  05 January 2012

C. Ruyer-Quil ,
S. Chakraborty  and
B. S. Dandapat
C. Ruyer-Quil*
Affiliation:
Université Pierre et Marie Curie – Laboratoire FAST, campus universitaire, 91405 Orsay, France
S. Chakraborty
Affiliation:
Université Pierre et Marie Curie – Laboratoire FAST, campus universitaire, 91405 Orsay, France
B. S. Dandapat
Affiliation:
Sikkim Manipal Institute of Technology, Majitar, Rangpo, 737 132, East Sikkim, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a power-law fluid flowing down an inclined plane under the action of gravity. The divergence of the viscosity at zero strain rate is taken care of by introducing a Newtonian plateau at small strain rate. 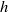Two-equation models are formulated within the framework of lubrication theory in terms of the exact mass balance and an averaged momentum equation, which form a set of evolution equations for the film thickness , a local velocity amplitude or the flow rate 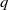. The models account for the streamwise diffusion of momentum. Comparisons with Orr–Sommerfeld stability analysis and with direct numerical simulation (DNS) show convincing agreement in both linear and nonlinear regimes. The influence of shear-thinning or shear-thickening on the primary instability is shown to be non-trivial. A destabilization of the base flow close to threshold is promoted by the shear-thinning effect, whereas, further from threshold, it tends to stabilize the base flow when the viscous damping of short waves becomes dominant. A reverse situation is observed in the case of shear-thickening fluids. Shear-thinning accelerates solitary waves and promotes a subcritical onset of travelling waves at larger wavenumber than the linear cut-off wavenumber. A conditional stability of the base flow is thus observed. This phenomenon results from a reduction of the effective viscosity at the free surface. When compared with DNS, simulations of the temporal response of the film based on weighted residual models satisfactorily capture the conditional stability of the film.

JFM classification

Complex Fluids: Complex Fluids Geophysical and Geological Flows: Shallow water flows Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 220 - 256
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alekseenko, S. V., Nakoryakov, V. E. & Pokusaev, B. G. 1994 Wave Flow in Liquid Films, 3rd edn. Begell House.CrossRefGoogle Scholar
2.Amaouche, M., Djema, A. & Bourdache, L. 2009 A modified Shkadov’s model for thin film flow of a power law fluid over an inclined surface. C. R. Mécanique 337 (1), 48–52.CrossRefGoogle Scholar
3.Balmforth, N. J. & Liu, J. J. 2004 Roll waves in mud. J. Fluid Mech. 519, 33–54.CrossRefGoogle Scholar
4.Bewersdorff, H.-W. & Singh, R. P. 1988 Rheological and drag reduction characteristics of xanthan gum solutions. Rheol. Acta 27, 617–627.CrossRefGoogle Scholar
5.Brevdo, L., Laure, P., Dias, F. & Bridges, T. J. 1999 Linear pulse structure and signaling in a film flow on an inclined plane. J. Fluid Mech. 396, 37–71.CrossRefGoogle Scholar
6.Chang, H.-C. & Demekhin, E. A. 2000 Coherent structures, self similarity, and universal roll-wave coarsening dynamics. Phys. Fluids 12 (9), 2268–2278.CrossRefGoogle Scholar
7.Chang, H.-C. & Demekhin, E. A. 2002 Complex Wave Dynamics on Thin Films. Elsevier.Google Scholar
8.Chang, H.-C., Demekhin, E. A., Kalaidin, E. & Ye, Y. 1996 Coarsening dynamics of falling-film solitary waves. Phys. Rev. E 54, 1467–1477.CrossRefGoogle ScholarPubMed
9.Chang, H.-C., Demekhin, E. A. & Kopelevitch, D. I. 1993 Nonlinear evolution of waves on a vertically falling film. J. Fluid Mech. 250, 433–480.CrossRefGoogle Scholar
10.Choppe, E., Puaud, F., Nicolai, T. & Benyahia, L. 2010 Rheology of xanthan solutions as a function of temperature, concentration and ionic strength. Carbohydrate Polymers 82, 1228–1235.CrossRefGoogle Scholar
11.Dandapat, B. S. & Mukhopadhyay, A. 2001 Waves on a film of power-law fluid flowing down an inclined plane at moderate Reynolds number. Fluid Dyn. Res. 29, 199–220.CrossRefGoogle Scholar
12.Dandapat, B. S. & Mukhopadhyay, A. 2003 Waves on the surface of a falling power-law fuid. Intl J. Non-Linear Mech. 38, 21–38.CrossRefGoogle Scholar
13.Dietze, G. F., Al-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.CrossRefGoogle Scholar
14.Dietze, G. F., Leefken, A. & Kneer, R. 2008 Investigation of the backflow phenomenon in falling liquid films. J. Fluid Mech. 595, 435–459.CrossRefGoogle Scholar
15.Doedel, E. J. 2008 AUTO07p: Continuation and Bifurcation Software for Ordinary Differential Equations. Montreal Concordia University.Google Scholar
16.Dressler, R. F. 1949 Mathematical solution of the problem of roll-waves in inclined open channels. Commun. Pure Appl. Maths 2, 149–194.CrossRefGoogle Scholar
17.Fernández-Nieto, E. D., Noble, P. & Vila, J.-P. 2010 Shallow water equations for non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 165 (13–14), 712–732.CrossRefGoogle Scholar
18.Fonder, N. & Xanthoulis, S. 2007 Roman aqueduct and hydraulic engineering: case of Nîmes aqueduct and its Pont du Gard bridge. Water Sci. Technol. Water Supply 7, 121–129.CrossRefGoogle Scholar
19.Griskey, R. G., Nechrebecki, D. G., Notheis, P. J. & Balmer, R. T. 1985 Rheological and pipeline flow behaviour of corn starch dispersion. J. Rheol. 29, 349–360.CrossRefGoogle Scholar
20.Hwang, C.-C., Chen, J.-L., Wang, J.-S. & Lin, J.-S. 1994 Linear stability of power law liquid film flows down an inclined plane. J. Phys. D: Appl. Phys. 27, 2297–2301.CrossRefGoogle Scholar
21.Julien, P. Y. & Hartley, D. M. 1986 Formation of roll waves in laminar sheet flow. J. Hydraul. Res. 24, 5–17.CrossRefGoogle Scholar
22.Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2011 Falling liquid films. In Applied Mathematical Sciences, 1st edn. 176. Springer.Google Scholar
23.Kapitza, P. L. & Kapitza, S. P. 1949 Wave flow of thin layers of a viscous fluid: III. experimental study of undulatory flow conditions. In Collected papers of P. L. Kapitza (1965) (ed. D. T. Haar), pp. 690–709. Pergamon, (Original paper in Russian: Zh. Ekper. Teor. Fiz.  19, 105–120).Google Scholar
24.Kawahara, T. 1983 Formation of saturated solitons in a nonlinear dispersive system with instability and dissipation. Phys. Rev. Lett. 51, 381–383.CrossRefGoogle Scholar
25.Kawahara, T. & Toh, S. 1988 Pulse interactions in an unstable dissipative-dispersive nonlinear system. Phys. Fluids 31, 2103–2111.CrossRefGoogle Scholar
26.Lindner, A., Bonn, D. & Meunier, J. 2000 Viscous fingering in a shear-thinning fluid. Phys. Fluids 12, 256–261.CrossRefGoogle Scholar
27.Liu, J. & Gollub, J. P. 1994 Solitary wave dynamics of film flows. Phys. Fluids 6, 1702–1712.CrossRefGoogle Scholar
28.Liu, K. & Mei, C. C. 1994 Roll waves on a layer of a muddy fluid flowing down a gentle slope—a Bingham model. Phys. Fluids 6 (8), 2577–2589.CrossRefGoogle Scholar
29.Liu, Q. Q., Chen, L., Li, J. C. & Singh, V. P. 2005 Roll waves in overland flow. J. Hydrol. Engng 10 (2), 110–117.CrossRefGoogle Scholar
30.Malamataris, N. A., Vlachogiannis, M. & Bontozoglou, V. 2002 Solitary waves on inclined films: flow structure and binary interactions. Phys. Fluids 14, 1082–1094.CrossRefGoogle Scholar
31.Manneville, P. 1990 Dissipative Structures and Weak Turbulence. Academic Press.Google Scholar
32.Miladinova, S., Lebonb, G. & Toshev, E. 2004 Thin-film flow of a power-law liquid falling down an inclined plate. J. Non-Newtonian Fluid Mech. 122, 69–78.CrossRefGoogle Scholar
33.Millet, S., Botton, V., Rousset, F. & Hadid, H. B. 2008 Wave celerity on a shear-thinning fluid film flowing down an incline. Phys. Fluids 20, 031701.CrossRefGoogle Scholar
34.Ng, C.-O. & Mei, C. C. 1994 Roll waves on a shallow layer of mud modelled as a power-law fluid. J. Fluid Mech. 263, 151–184.CrossRefGoogle Scholar
35.Pascal, J. P. & D’Alesio, S. J. D. 2007 Instability of power-law fluid flows down an incline subjected to wind stress. Appl. Math. Model. 31, 1229–1248.CrossRefGoogle Scholar
36.Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190, 572–600.CrossRefGoogle Scholar
37.Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
38.Pradas, M., Tseluiko, D. & Kalliadasis, S. 2011 Rigorous coherent-structure theory for falling liquid films: viscous dispersion effects on bound-state formation and self-organization. Phys. Fluids 23, 044104.CrossRefGoogle Scholar
39.Ramaswamy, B., Chippada, S. & Joo, S. W. 1996 A full-scale numerical study of interfacial instabilities in thin-film flows. J. Fluid Mech. 325, 163–194.CrossRefGoogle Scholar
40.Rousset, F., Millet, S., Botton, V. & Hadid, H. B. 2007 Temporal stability of Carreau fluid flow down an incline. Trans. ASME: J. Fluids Engng 129 (7), 913–920.Google Scholar
41.Ruyer-Quil, C. & Manneville, P. 2000 Improved modelling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
42.Ruyer-Quil, C., Treveleyan, P., Giorgiutti-Dauphiné, F., Duprat, C. & Kalliadasis, S. 2008 Modelling film flows down a fibre. J. Fluid Mech. 603, 431–462.CrossRefGoogle Scholar
43.Scheid, B., Ruyer-Quil, C. & Manneville, P. 2006 Wave patterns in film flows: modelling and three-dimensional waves. J. Fluid Mech. 562, 183–222.CrossRefGoogle Scholar
44.Scheid, B., Ruyer-Quil, C., Thiele, U., Kabov, O. A., Legros, J. C. & Colinet, P. 2005 Validity domain of the Benney equation including the Marangoni effect for closed and open flows. J. Fluid Mech. 527, 303–335.CrossRefGoogle Scholar
45.Seevaratnam, G. K., Suo, Y., Ramé, E., Walker, L. M. & Garoff, S. 2007 Dynamic wetting of shear thinning fluids. Phys. Fluids 19, 012103.CrossRefGoogle Scholar
46.Sisoev, G. M., Dandapat, B. S., Matveyev, K. S. & Mukhopadhyay, A. 2007 Bifurcation analysis of the travelling waves on a falling power-law fluid film. J. Non-Newtonian Fluid Mech. 141, 128–137.CrossRefGoogle Scholar
47.Smith, M. K. 1990 The mechanism for the long-wave instability in thin liquid films. J. Fluid Mech. 217, 469–485.CrossRefGoogle Scholar
48.Usha, R., Millet, S., BenHadid, H. & Rousset, F. 2011 Shear-thinning film on a porous substrate: stability analysis of a one-sided model. Chem. Engng Sci. 66 (22), 5614–5627.CrossRefGoogle Scholar
49.Vlachogiannis, M. & Bontozoglou, V. 2001 Observations of solitary wave dynamics of film flows. J. Fluid Mech. 435, 191.CrossRefGoogle Scholar
50.Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley-Interscience.Google Scholar