Published online by Cambridge University Press: 16 October 2015
The motion of a liquid in an open cylindrical tank rotating at a constant rate around its vertical axis of symmetry, a configuration called Newton’s bucket, is investigated using a linear stability approach. This flow is shown to be affected by several families of waves, all weakly damped by viscosity. The wave families encountered correspond to: surface waves which can be driven either by gravity or centrifugal acceleration, inertial waves due to Coriolis acceleration which are singular in the inviscid limit, and Rossby waves due to height variations of the fluid layer. These waves are described in the inviscid and viscous cases by means of mathematical considerations, global stability analysis and various asymptotic methods; and their properties are investigated over a large range of parameters 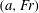 $(a,Fr)$, with
$(a,Fr)$, with  $a$ the aspect ratio and
$a$ the aspect ratio and 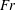 $Fr$ the Froude number.
$Fr$ the Froude number.