Published online by Cambridge University Press: 29 August 2023
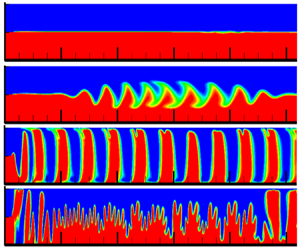
This study presents the results of a numerical simulation of two horizontal flows of miscible magnetic and non-magnetic fluids at low Reynolds numbers in a vertical uniform magnetic field. The problem is solved by taking into account the dependence of the viscosity and magnetization of the fluid on the concentration of the magnetic phase, and the dependence of the magnetic field on the concentration. Four flow modes are found: the diffusion mixing mode with a flat diffusion front, the wave mode and two different plug flow modes. In the first of them, the growing wave instability forms the plugs, whereas in the second, the growing magnetostatic instability does. A combination of dimensionless criteria is found that determines the transition from one mode to another. The dependences of the phase velocity of the waves on the diffusion front and the period of the oscillations of the front near the point of the confluence of the two flows on dimensionless criteria are found.