Published online by Cambridge University Press: 26 July 2019
The spectrum of turbulence kinetic energy for homogeneous turbulence is generally computed using the Fourier transform of the velocity field from physical three-dimensional space to wavenumber 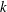 $k$. This analysis works well for single-phase homogeneous turbulent flows. In the case of multiphase turbulent flows, instead, the velocity field is non-smooth at the interface between the carrier fluid and the dispersed phase; thus, the energy spectra computed via Fourier transform exhibit spurious oscillations at high wavenumbers. An alternative definition of the spectrum uses the wavelet transform, which can handle discontinuities locally without affecting the entire spectrum while additionally preserving spatial information about the field. In this work, we propose using the wavelet energy spectrum to study multiphase turbulent flows. Also, we propose a new decomposition of the wavelet energy spectrum into three contributions corresponding to the carrier phase, droplets and interaction between the two. Lastly, we apply the new wavelet-decomposition tools in analysing the direct numerical simulation data of droplet-laden decaying isotropic turbulence (in absence of gravity) of Dodd & Ferrante (J. Fluid Mech., vol. 806, 2016, pp. 356–412). Our results show that, in comparison to the spectrum of the single-phase case, the droplets (i) do not affect the carrier-phase energy spectrum at high wavenumbers (
$k$. This analysis works well for single-phase homogeneous turbulent flows. In the case of multiphase turbulent flows, instead, the velocity field is non-smooth at the interface between the carrier fluid and the dispersed phase; thus, the energy spectra computed via Fourier transform exhibit spurious oscillations at high wavenumbers. An alternative definition of the spectrum uses the wavelet transform, which can handle discontinuities locally without affecting the entire spectrum while additionally preserving spatial information about the field. In this work, we propose using the wavelet energy spectrum to study multiphase turbulent flows. Also, we propose a new decomposition of the wavelet energy spectrum into three contributions corresponding to the carrier phase, droplets and interaction between the two. Lastly, we apply the new wavelet-decomposition tools in analysing the direct numerical simulation data of droplet-laden decaying isotropic turbulence (in absence of gravity) of Dodd & Ferrante (J. Fluid Mech., vol. 806, 2016, pp. 356–412). Our results show that, in comparison to the spectrum of the single-phase case, the droplets (i) do not affect the carrier-phase energy spectrum at high wavenumbers (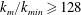 $k_{m}/k_{min}\geqslant 128$), (ii) increase the energy spectrum at high wavenumbers (
$k_{m}/k_{min}\geqslant 128$), (ii) increase the energy spectrum at high wavenumbers (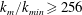 $k_{m}/k_{min}\geqslant 256$) by increasing the interaction energy spectrum at these wavenumbers and (iii) decrease the energy at low wavenumbers (
$k_{m}/k_{min}\geqslant 256$) by increasing the interaction energy spectrum at these wavenumbers and (iii) decrease the energy at low wavenumbers (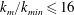 $k_{m}/k_{min}\leqslant 16$) by increasing the dissipation rate at these wavenumbers.
$k_{m}/k_{min}\leqslant 16$) by increasing the dissipation rate at these wavenumbers.