Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-09T22:07:13.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Wavelet analysis of near-field pressure fluctuations generated by a subsonic jet

Published online by Cambridge University Press:  28 March 2012

S. Grizzi  and
R. Camussi
S. Grizzi
Affiliation:
INSEAN, Italian Hydrodynamic Institute, via di Vallerano 139, 00128 Roma, Italy
R. Camussi*
Affiliation:
Dipartimento di Ingegneria Meccanica e Industriale, Universitá Roma Tre, via della Vasca Navale 79, 00146 Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

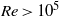An experimental study of the pressure field generated by a subsonic, single stream, round jet is presented. The investigation is conducted in the near-field region at subsonic Mach numbers (up to 0.9) and Reynolds numbers . The main task of the present work is the analysis of the near-field acoustic pressure and the characterization of its spectral properties. To this aim, a novel post-processing technique based on the application of wavelet transforms is presented. The method accomplishes the separation of nearly Gaussian background fluctuations, interpreted as acoustic pressure, from intermittent pressure peaks induced by the hydrodynamic components. With respect to more standard approaches based on Fourier filtering, the new technique permits one to recover the whole frequency content of both the acoustic and the hydrodynamic contributions and to reconstruct them as independent signals in the time domain. The near-field acoustic pressure is characterized in terms of spectral content, sound pressure level and directivity. The effects of both the Mach number and the distance from the jet axis are analysed and the results are compared with published far-field observations and theoretical predictions. Simultaneous velocity/pressure measurements have been also performed using a hot-wire probe and a microphone pair in the near field. It is shown that the cross-correlation between the near-field acoustic pressure and the axial velocity is large (of the order of 0.2) in the potential core region whereas large velocity/hydrodynamic pressure correlations are located at the nozzle exit and downstream of the potential core.

JFM classification

Turbulent Flows: Intermittency Acoustics: Jet noise Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 698 , 10 May 2012 , pp. 93 - 124
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abry, P., Fauve, S., Flandrin, P. & Laroche, C. 1994 Analysis of pressure fluctuations in swirling turbulent flows. J. Phys. II 4, 725–733.Google Scholar
2. Arndt, R., Long, D. & Glauser, M. 1997 The proper orthogonal decomposition of pressure fluctuations surrounding a turbulent jet. J. Fluid Mech. 340, 1–33.CrossRefGoogle Scholar
3. Becker, H. A., Hottel, H. C. & Williams, G. C. 1967 The concentration field of a free jet. J. Fluid Mech. 30, 285–303.CrossRefGoogle Scholar
4. Bogey, C. & Bailly, C. 2007 An analysis of the correlations between the turbulent flow and the sound pressure fields of subsonic jets. J. Fluid Mech. 538, 71–97.CrossRefGoogle Scholar
5. Camussi, R. & Guj, G. 1999 Experimental analysis of intermittent coherent structures in the near field of a high Re turbulent jet flow. Phys. Fluids 11, 423–431.Google Scholar
6. Camussi, R., Jacob, M. C., Grilliat, J. & Caputi Gennaro, G. 2010 Experimental study of a tip leakage flow: wavelet analysis of pressure fluctuations. J. Fluid Mech. 660, 87–113.Google Scholar
7. Camussi, R., Robert, G. & Jacob, M. C. 2008 Cross-wavelet analysis of wall pressure fluctuations beneath incompressible turbulent boundary layers. J. Fluid Mech. 617, 11–30.CrossRefGoogle Scholar
8. Cavalieri, A. V. G., Jordan, P., Agarwal, A. & Gervais, Y. 2011 Jittering wave-packet models for subsonic jet noise. J. Sound Vib. 330, 4474–4492.Google Scholar
9. Coiffet, F., Jordan, P., Delville, J., Gervais, Y. & Richaud, F. 2006 Coherent structures in subsonic jets: a quasi-irrotational source mechanism. Intl J. Aeroacoust. 5 (1), 67–89.Google Scholar
10. Crighton, D. G. 1981 Acoustics as a branch of fluid mechanics. J. Fluid Mech. 106, 261–298.Google Scholar
11. Daubechies, I. 1992 Ten Lectures on Wavelets. SIAM.Google Scholar
12. Donoho, D. & Johnstone, I. 1994 Ideal spatial adaptation via wavelet shrinkage. Biometrika 81, 425–455.CrossRefGoogle Scholar
13. Farge, M. 1992 Wavelet transforms and their applications to turbulence. Ann. Rev. Fluid Mech. 24, 395–457.CrossRefGoogle Scholar
14. Ffowcs-Williams, J. 1992 Noise source mechanisms. In Modern Methods in Analytical Acoustics (ed. Crighton, D. G., Dowling, A. P., Ffowcs Williams, J. E., Heckl, M. A. & Leppington, F. A. ). Lecture Notes , pp. 313–354. Springer.Google Scholar
15. Fuchs, H. V. 1972 Space correlations of the fluctuating pressure in subsonic turbulent jets. J. Sound Vib. 23 (1), 77–99.CrossRefGoogle Scholar
16. George, W. K., Beuther, P. D. & Arndt, R. E. A. 1984 Pressure spectra in turbulent free shear flows. J. Fluid Mech. 148, 155–191.CrossRefGoogle Scholar
17. Goldstein, M. E. 1984 Aeroacoustics of turbulent shear flows. Annu. Rev. Fluid Mech. 16, 263–285.CrossRefGoogle Scholar
18. Guitton, A., Jordan, P., Laurendeau, E. & Delville, J. 2007 Velocity dependence of the near pressure field of subsonic jets: understanding the associated source mechanisms. AIAA Paper 2007-3661.CrossRefGoogle Scholar
19. Guj, G., Carley, M. & Camussi, R. 2003 Acoustic identification of coherent structures in a turbulent jet. J. Sound Vib. 259, 1037–1065.Google Scholar
20. Hileman, J. I., Thurow, B. S., Caraballo, E. J. & Samimy, M. 2005 Large-scale structure evolution and sound emission in high-speed jets: real-time visualization with simultaneous acoustic measurements. J. Fluid Mech. 544, 277–307.CrossRefGoogle Scholar
21. Horstman, C. C. & Rose, W. C. 1975 Hot-wire anemometry in transonic flow, NASA Technical Memorandum X-62 495.Google Scholar
22. Howe, W. L. 1960 Similarity of far noise fields of jets. NASA Technical Report R-52.Google Scholar
23. Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1980 Vortex pairing in a circular jet under controlled excitation. Part 2. Coherent structure dynamics. J. Fluid Mech. 101, 493–544.Google Scholar
24. Jones, B. G., Adrian, R. J., Nithianandan, C. K. & Planchon, H. P. 1979 Spectra of turbulent static pressure fluctuations in jet mixing layers. AIAA J. 17 (5), 449–457.Google Scholar
25. Jordan, P. & Gervais, Y. 2008 Subsonic jet aeroacoustics: associating experiment, modelling and simulation. Exp. Fluids 44, 1–21.Google Scholar
26. Kerhervé, F., Guitton, A., Jordan, P., Delville, J., Fortuné, V., Gervais, Y. & Tinney, C. 2008 Identifying the dynamics underlying the large scale jetnoise similarity spectra. AIAA paper 2008-3027.Google Scholar
27. Lee, I. & Sung, H. J. 2002 Multiple-arrayed pressure measurement for investigation of the unsteady flow structure of a reattaching shear layer. J. Fluid Mech. 463, 377–402.Google Scholar
28. Lighthill, M. J. 1952 On Sound Generated Aerodynamically: I. General Theory. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
29. Lilley, G. M. 1995 Jet noise classical theory and experiments. Aeroacoust. Flight Vehicles 1, 211–290.Google Scholar
30. Mallat, S. 1989 A theory for multiresolution signal decomposition: the wavelet representation. Trans. IEEE Pattern Anal. Machine Intell. 11, 674–693.Google Scholar
31. Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70 (1), 179–205.Google Scholar
32. Mollo-Christensen, E. 1967 Jet noise and shear flow instability seen from an experimenters viewpoint (similarity laws for jet noise and shear flow instability as suggested by experiments). J. Appl. Mech. 34, 1–7.CrossRefGoogle Scholar
33. Petersen, R. A. 1978 Influence of wave dispersion on vortex pairing in a jet. J. Fluid Mech. 89, 469–495.CrossRefGoogle Scholar
34. Picard, C. & Delville, J. 1999 Pressure velocity coupling in a subsonic round jet. Engng Turbul. Model. Experiments 4, 443–452.Google Scholar
35. Poggie, J. & Smits, A. J. 1997 Wavelet analysis of wall-pressure fluctuations in a supersonic blunt fin flow. AIAA J. 35, 1597–1603.CrossRefGoogle Scholar
36. Rajaratnam, N. 1976 Turbulent Jets. Elsevier Publishing Co..Google Scholar
37. Ribner, H. S. 1964 The generation of sound by turbulent jets. Adv. Appl. Mech. VIII, 103–182.Google Scholar
38. Ruppert-Felsot, J., Farge, M. & Petitjeans, P. 2009 Wavelet tools to study intermittency: application to vortex bursting. J. Fluid Mech. 636, 427–453.Google Scholar
39. So, R. M. C., Zhu, J. Y. Z., Otugen, M. V. & Huang, B. C. 1990 Some measurements in a binary gas jet. Exp. Fluids 9, 273–284.Google Scholar
40. Suzuki, T. M. & Colonius, T. 2007 Instability waves in a subsonic round jet detected using a near-field phased microphone array. J. Fluid Mech. 565, 197–226.Google Scholar
41. Tam, C. K. W. 1998 Jet noise since 1952. Theoret. Computat. Fluid Dyn. 10, 393–405.CrossRefGoogle Scholar
42. Tam, C. K. W., Golebiowski, M. & Seiner, J. M. 1996 On the two components of turbulent mixing noise from supersonic jets. AIAA paper 96-1716.Google Scholar
43. Tam, C. K. W., Viswanathan, K., Ahuja, K. K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.CrossRefGoogle Scholar
44. Tanna, H. K. 1977 An experimental study of jet noise. J. Sound Vib. 50, 429–444.CrossRefGoogle Scholar
45. Tinney, C. E. & Jordan, P. 2008 The near pressure field of co-axial subsonic jets. J. Fluid Mech. 611, 175–204.Google Scholar
46. Tinney, C. E., Jordan, P., Delville, J., Hall, A. M. & Glauser, M. N. 2007 A time-resolved estimate of the turbulence and sound source mechanisms in a subsonic jet flow. J. Turbul. 8 (7), 1–20.Google Scholar
47. Ukeiley, L. S. & Ponton, M. K. 2004 On the near field pressure of a transonic axisymmetric jet. Intl J. Aeroacoust. 3 (1), 43–66.CrossRefGoogle Scholar
48. Zaman, K. B. M. Q. 1986 Flow field and near and far sound field of a subsonic jet. J. Sound Vib. 106 (1), 1–16.CrossRefGoogle Scholar