Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T09:15:28.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave turbulence in the two-layer ocean model

Published online by Cambridge University Press:  01 September 2014

Katie L. Harper ,
Sergey V. Nazarenko ,
Sergey B. Medvedev  and
Colm Connaughton
Katie L. Harper*
Affiliation:
Mathematics Institute, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK
Sergey V. Nazarenko
Affiliation:
Mathematics Institute, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK Laboratoire SPHYNX, Service de Physique de l’Etat Condense, DSM, IRAMIS, CEA, Saclay, CNRS URA 2464, 91191, Gif-sur-Yvette, France
Sergey B. Medvedev
Affiliation:
Institute of Computational Technologies SD RAS, Lavrentjev Avenue 6, Novosibirsk, 630090, Russia
Colm Connaughton
Affiliation:
Mathematics Institute, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK Centre for Complexity Science, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK Okinawa Institute of Science and Technology Graduate University, 1919-1 Tancha Onna-son, Okinawa 904-0495, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper looks at the two-layer ocean model from a wave-turbulence (WT) perspective. A symmetric form of the two-layer kinetic equation for Rossby waves is derived using canonical variables, allowing the turbulent cascade of energy between the barotropic and baroclinic modes to be studied. It is already well known that in two-layers, energy is transferred via triad interactions from the large-scale baroclinic modes to the baroclinic and barotropic modes at the Rossby deformation scale, where barotropization takes place, and from there to the large-scale barotropic modes via an inverse transfer. However, by applying WT theory, we find that energy is transferred via dominant 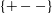$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\{+--\}$ triads with one barotropic component and two baroclinic components, and that the direct transfer of energy is local and the inverse energy transfer is non-local. We study this non-locality using scale separation and obtain a system of coupled equations for the small-scale baroclinic component and the large-scale barotropic component. Since the total energy of the small-scale component is not conserved, but the total barotropic plus baroclinic energy is conserved, the baroclinic energy loss at small scales will be compensated by the growth of the barotropic energy at large scales. Using the frequency resonance condition, we show that in the presence of the beta-effect this transfer is mostly anisotropic and mostly to the zonal component.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Turbulent Flows: Wave-turbulence interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 309 - 327
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balk, A. & Nazarenko, S. 1990 Physical realizability of anisotropic weak-turbulence Kolmogorov spectra. Sov. Phys. JETP 70, 1031–1041.Google Scholar
Balk, A., Nazarenko, S. & Zakharov, V. 1990 On the non-local turbulence of drift type waves. Phys. Lett. A 146, 217–221.CrossRefGoogle Scholar
Balk, A., Nazarenko, S. & Zakharov, V. 1991 A new invariant for drift turbulence. Phys. Lett. A 152, 276–280.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratifed turbulence. J. Atmos. Sci. 52, 4410–4428.2.0.CO;2>CrossRefGoogle Scholar
Bedard, R., Lukaschuk, S. & Nazarenko, S. 2013 Non-stationary regimes of surface gravity wave turbulence. J. Expl Theor. Phys. Lett. 97, 529–535.Google Scholar
Charney, J. 1948 On the scale of atmospheric motions. Geofys. Publ. Oslo 17, 1–17.Google Scholar
Charney, J. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1094.2.0.CO;2>CrossRefGoogle Scholar
Connaughton, C., Nazarenko, S. & Quinn, B.2010 Non-local wave turbulence in the Charney–Hasegawa–Mima equation: a short review. arXiv:1012.2714.Google Scholar
Connaughton, C., Nazarenko, S. & Quinn, B. 2011 Feedback of zonal flows on wave turbulence driven by small-scale instability in the Charney–Hasegawa–Mima model. Europhys. Lett. 96, 25001.Google Scholar
Fjørtoft, R. 1953 On the changes in the spectral distribution of kinetic energy for two-dimensional non-divergent flow. Tellus 5, 225–230.Google Scholar
Galperin, B., Sukoriansky, S., Dikovskaya, N., Read, P., Yamazaki, Y. & Wordsworth, R. 2006 Anisotropic turbulence and zonal jets in rotating flows with a beta-effect. Nonlinear Process. Geophys. 13, 83–98.Google Scholar
Herbert, C. 2014 Nonlinear energy transfers and phase diagrams for geostrophically balanced rotating-stratified flows. Phys. Rev. E 89, 033008.Google Scholar
Janssen, P. 2008 Progress in ocean wave forecasting. J. Comput. Phys. 227, 3572–3594.Google Scholar
Kozlov, O., Reznik, G. & Soomere, T. 1987 Kinetic equation for Rossby waves in two-layer ocean. Izv. Akad. Nauk SSSR Ser. Fiz. Atmosfer. i Okeana 23, 1165–1173.Google Scholar
Kraichnan, R. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
L’vov, V., Nazarenko, S. & Skrbek, L. 2006 Energy spectra of developed turbulence in helium superfluids. J. Low Temp. Phys. 145, 125–142.Google Scholar
McWilliams, J. 2006 Fundamentals of Geophysical Fluid Dynamics. Cambridge University Press.Google Scholar
Nazarenko, S. 2011 Wave Turbulence, Lecture Notes in Physics, vol. 825. Springer.Google Scholar
Nazarenko, S., Kevlahan, N. & Dubrulle, B. 1999 A WKB theory for rapid distortion of inhomogeneous turbulence. J. Fluid Mech. 390, 325–348.CrossRefGoogle Scholar
Nazarenko, S., Kevlahan, N. & Dubrulle, B. 2000 Nonlinear RDT theory of near-wall turbulence. Physica D 139, 158–176.CrossRefGoogle Scholar
Nazarenko, S. & Quinn, B. 2009 Triple cascade behaviour in QG and drift turbulence and the generation of zonal jets. Phys. Rev. Lett. 103, 118501.Google Scholar
Phillips, N. 1951 A simple three-dimensional model for the study of large-scale extra-tropical flow patterns. J. Meteorol. 8, 381–394.Google Scholar
Rhines, P. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443.Google Scholar
Rhines, P. 2007 The dynamics of unsteady currents. In The Sea, vol. VI (ed. Goldberg, E. D.), pp. 189–318. John Wiley and Sons, Inc.Google Scholar
Rhines, P. 1979 Geostrophic turbulence. Annu. Rev. Fluid Mech. 11, 401–441.Google Scholar
Salmon, R. 1978 Two-layer quasi-geostrophic turbulence in a simple special case. Geophys. Astrophys. Fluid Dyn. 10, 25–52.Google Scholar
Salmon, R. 1980 Baroclinic instability and geostrophic turbulence. Geophys. Astrophys. Fluid Dyn. 15, 167–211.Google Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.Google Scholar
Smith, K. & Vallis, G. 2001 Scales and equilibration of mid-ocean eddies. Freely decaying flow. J. Phys. Oceanogr. 31, 554–571.Google Scholar
Smith, K. & Vallis, G. 2002 The scales and equilibration of midocean eddies: forced-dissipative flow. J. Phys. Oceanogr. 32, 1699–1721.Google Scholar
Tronko, N., Nazarenko, S. & Galtier, S. 2013 Weak turbulence in two-dimensional magnetohydrodynamics. Phys. Rev. E 87, 033103.Google Scholar
Vallis, G. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Vallis, G. & Maltrud, M. E. 1993 Generation of mean flows and jets on a beta-plane and over topography. J. Phys. Oceanogr. 23, 1346–1362.Google Scholar
Venaille, A., Vallis, G. & Griffies, S. 2012 The catalytic role of beta effect in barotropization processes. J. Fluid Mech. 709, 490–515.Google Scholar
Zakharov, V. & Filonenko, N. 1967 Energy spectrum for stochastic oscillations of the surface of a liquid. Sov. Phys. Dokl. 11, 881–884.Google Scholar
Zakharov, V., L’vov, V. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer.CrossRefGoogle Scholar