Article contents
Water wave cloaking using a floating composite plate
Published online by Cambridge University Press: 23 December 2022
Abstract
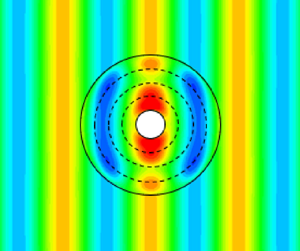
The trajectory of surface gravity waves in the potential flow regime is affected by the gravitational acceleration, water density and sea bed depth. Although the gravitational acceleration and water density are approximately constant, the effect of water depth on surface gravity waves exponentially decreases as the water depth increases. In shallow water, cloaking an object from surface waves by varying the sea bed topography is possible, however, as the water depth increases, cloaking becomes a challenge because there is no physical parameter to be engineered and subsequently affects the wave propagation. In order to create an omnidirectional cylindrical cloaking device for finite-depth/deep-water waves, we propose an elastic composite plate that floats on the surface around a to-be-cloaked cylinder. The composite plate is made of axisymmetric, homogeneous and isotropic annular thin rings which provide adjustable degrees of freedom to engineer and affect the wave propagation. We first develop a pseudo-spectral method to efficiently determine the wave solution for a floating composite plate. Next, we optimise the physical parameters of the plate (i.e. flexural rigidity and mass of every ring) using an evolutionary algorithm to minimise the energy of scattered waves from the object and therefore cloak the inner cylinder from incident waves. We show that the optimised cloak reduces the energy of scattered waves as high as 99 % for the target wave number. We quantify the effectiveness of our cloak with different parameters of the plate and show that varying the flexural rigidity is essential to control wave propagation and the cloaking structure needs to be at least made of four rings with a radius of at least three times of the cloaked region. We quantify the wave drift force exerted on the structures and show that the optimised plate reduces the exerted force by 99.9 %. The proposed cloak, due to its structural simplicity and effectiveness in reducing the wave drift force, may have potential applications in cloaking offshore structures from water waves.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by



