Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T14:55:55.503Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall-bounded flow over a realistically rough superhydrophobic surface

Published online by Cambridge University Press:  28 June 2019

Karim Alamé Open the ORCID record for Karim Alamé [Opens in a new window]  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Karim Alamé
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation (DNS) is performed for two wall-bounded flow configurations: laminar Couette flow at 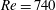$Re=740$ and turbulent channel flow at 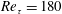$Re_{\unicode[STIX]{x1D70F}}=180$, where $\unicode[STIX]{x1D70F}$ is the shear stress at the wall. The top wall is smooth and the bottom wall is a realistically rough superhydrophobic surface (SHS), generated from a three-dimensional surface profile measurement. The air–water interface, which is assumed to be flat, is simulated using the volume-of-fluid (VOF) approach. The two flow cases are studied with varying interface heights 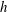$h$ to understand its effect on slip and drag reduction (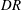$DR$). For the laminar Couette flow case, the presence of the surface roughness is felt up to 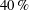$40\,\%$ of the channel height in the wall-normal direction. Nonlinear dependence of 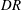$DR$ on 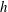$h$ is observed with three distinct regions. A nonlinear curve fit is obtained for gas fraction $\unicode[STIX]{x1D719}_{g}$ as a function of 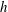$h$, where 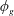$\unicode[STIX]{x1D719}_{g}$ determines the amount of slip area exposed to the flow. A power law fit is obtained from the data for the effective slip length as a function of 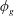$\unicode[STIX]{x1D719}_{g}$ and is compared to those derived for structured geometry. For the turbulent channel flow, statistics of the flow field are compared to that of a smooth wall to understand the effects of roughness and 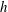$h$. Four cases are simulated ranging from fully wetted to fully covered and two intermediate regions in between. Scaling laws for slip length, slip velocity, roughness function and 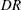$DR$ are obtained for different penetration depths and are compared to past work for structured geometry. 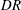$DR$ is shown to depend on a competing effect between slip velocity and turbulent losses due to the Reynolds shear stress contribution. Presence of trapped air in the cavities significantly alters near-wall flow physics where we examine near-wall structures and propose a physical mechanism for their behaviour. The fully wetted roughness increases the peak value of turbulent intensities, whereas the presence of the interface suppresses them. The pressure fluctuations have competing contributions between turbulent pressure fluctuations and stagnation due to asperities, the near-wall structure is altered and breaks down with increasing slip. Overall, there exists a competing effect between the interface and the asperities, the interface suppresses turbulence whereas the asperities enhance them. The present work demonstrates DNS over a realistic multiphase SHS for the first time, to the best of our knowledge.

JFM classification

Flow Control: Drag reduction Multiphase and Particle-laden Flows: Multiphase flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 977 - 1019
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C. H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Barthlott, W. & Neinhuis, C. 1997 Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 202, 1–8.Google Scholar
Belyaev, A. V. & Vinogradova, O. I. 2010 Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 645, 489–499.Google Scholar
Bidkar, R. A., Leblanc, L., Kulkarni, A. J., Bahadur, V., Ceccio, S. L. & Perlin, M. 2014 Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 26 (8), 085108.Google Scholar
Bradshaw, P. 2000 A note on ‘critical roughness height’ and ‘transitional roughness’. Phys. Fluids 12 (6), 1611–1614.Google Scholar
Busse, A. & Sandham, N. D. 2012 Influence of an anisotropic slip-length boundary condition on turbulent channel flow. Phys. Fluids 24 (5), 055111.Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.Google Scholar
Cassie, A. B. D. & Baxter, S. 1944 Wettability of porous surfaces. Trans. Faraday Soc. 40, 546–551.Google Scholar
Choi, C. H. & Kim, C. J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001.Google Scholar
Cottin-Bizonne, C., Barrat, J. L., Bocquet, L. & Charlaix, É. 2003 Low-friction flows of liquid at nanopatterned interfaces. Nat. Mater. 2 (4), 237–240.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21 (8), 085103.Google Scholar
Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.Google Scholar
Emami, B., Tafreshi, H. V., Gad-el Hak, M. & Tepper, G. C. 2011 Predicting shape and stability of air-water interface on superhydrophobic surfaces with randomly distributed, dissimilar posts. Appl. Phys. Lett. 98 (20), 203106.Google Scholar
Fairhall, C. T., Abderrahaman-Elena, N. & García-Mayoral, R. 2019 The effect of slip and surface texture on turbulence over superhydrophobic surfaces. J. Fluid Mech. 861, 88–118.Google Scholar
Fang, G., Li, W., Wang, X. & Qiao, G. 2008 Droplet motion on designed microtextured superhydrophobic surfaces with tunable wettability. Langmuir 24, 11651–11660.Google Scholar
Frohnapfel, B., Hasegawa, Y. & Kasagi, N. 2010 Friction drag reduction through damping of the near-wall spanwise velocity fluctuations. Intl J. Heat Mass Transfer 31, 434–441.Google Scholar
Fu, M. K., Arenas, I., Leonardi, S. & Hultmark, M. 2017 Liquid-infused surfaces as a passive method of turbulent drag reduction. J. Fluid Mech. 824, 688–700.Google Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18 (5), 051703.Google Scholar
Furstner, R., Barthlott, W., Neinhuis, C. & Walzel, P. 2005 Wetting and self-cleaning properties of artificial superhydrophobic surfaces. Langmuir 21, 956–961.Google Scholar
Garcia-Mayoral, R. & Jiménez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369, 1412–1427.Google Scholar
Genzer, J. & Efimenko, K. 2006 Recent developments in superhydrophobic surfaces and their relevance to marine fouling: a review. Biofouling 22, 339–360.Google Scholar
Gogte, S., Vorobieff, P., Truesdell, R., Mammoli, A., van Swol, F., Shah, P. & Brinker, C. J. 2005 Effective slip on textured superhydrophobic surfaces. Phys. Fluids 17, 051701.Google Scholar
Hasegawa, Y., Frohnapfel, B. & Kasagi, N. 2011 Effects of spatially varying slip length on friction drag reduction in wall turbulence. J. Phys. 318, 022028.Google Scholar
Henoch, C., Krupenkin, T. N., Kolodner, P., Taylor, J. A., Hodes, M. S., Lyons, A. M., Peguero, C. & Breuer, K.2006 Turbulent drag reduction using superhydrophobic surfaces. AIAA Paper 2006–3192.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26 (9), 095102.Google Scholar
Jiménez, J. 1994 On the structure and control of near wall turbulence. Phys. Fluids 6 (2), 944–953.Google Scholar
Joseph, P., Cottin-Bizonne, C., Benoit, J.-M., Ybert, C., Journet, C., Tabeling, P. & Bocquet, L. 2006 Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97, 1–4.Google Scholar
Jung, S., Dorrestijn, M., Raps, D., Das, A., Megaridis, C. & Poulikakos, D. 2011 Are superhydrophobic surfaces best for icephobicity? Langmuir 27, 3059–3066.Google Scholar
Jung, T., Choi, H. & Kim, J. 2016 Effects of the air layer of an idealized superhydrophobic surface on the slip length and skin-friction drag. J. Fluid Mech. 790 (5), R1.Google Scholar
Jung, Y. C. & Bhushnan, B. 2009 Biomimetic structures for fluid drag reduction in laminar and turbulent flows. J. Phys. 22, 035104.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Li, Y., Alame, K. & Mahesh, K. 2016 Feature resolved simulations of turbulence over superhydrophobic surfaces. In Proceedings of the 31st Symposium on Naval Hydrodynamics. Monterey, USA.Google Scholar
Li, Y., Alame, K. & Mahesh, K. 2017 Feature-resolved computational and analytical study of laminar drag reduction by superhydrophobic surface. Phys. Rev. Fluids 2, 054002.Google Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G. H., Tuteja, A. & Katz, J. 2016 High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.Google Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Ma, R., Alamé, K. & Mahesh, K.2019 Direct numerical simulations of random rough surfaces in turbulent channel flow. AIAA Paper 2019–2137.Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197 (1), 215–240.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31.Google Scholar
Martell, M. B., Rothstein, J. P. & Perot, J. B. 2010 An analysis of superhydrophobic turbulent drag reduction mechanisms using direct numerical simulation. Phys. Fluids 22 (6), 065102.Google Scholar
Maynes, D., Jeffs, K., Woolford, B. & Webb, B. W. 2007 Laminar flow in microchannel with hydrophobic surface patterned microribs oriented parallel to the flow difrection. Phys. Fluids 19, 093603.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, 1–5.Google Scholar
Nizkaya, T. V., Asmolov, E. S. & Vinogradova, O. I. 2014 Gas cushion model and hydrodynamic boundary conditions for superhydrophobic textures. Phys. Rev. E 90, 043017.Google Scholar
Ou, J., Perot, B. & Rothstein, J. P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.Google Scholar
Ou, J. & Rothstein, J. P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.Google Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.Google Scholar
Park, H., Sun, G. & Kim, C.-J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.Google Scholar
Peguero, C. & Breuer, K. 2009 On drag reduction in turbulent channel flow over superhydrophobic surfaces. In Advances in Turbulence XII (ed. Eckhardt, B.), Springer Proceedings in Physics, vol. 132, pp. 233–236. Springer.Google Scholar
Philip, J. R. 1972a Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23 (3), 353–372.Google Scholar
Philip, J. R. 1972b Integral properties of flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23 (6), 960–968.Google Scholar
Rastegari, A. & Akhavan, R. 2018 The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets. J. Fluid Mech. 838, 68–104.Google Scholar
Rastegari, A. & Akhavan, R. 2019 On drag reduction scaling and sustainability bounds of superhydrophobic surfaces in high Reynolds number turbulent flows. J. Fluid Mech. 864, 327–347.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Rosenberg, B. J., Van Buren, T., Fu, M. K. & Smits, A. J. 2016 Turbulent drag reduction over air- and liquid- impregnated surfaces. Phys. Fluids 28 (1), 015103.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42 (1), 89–109.Google Scholar
Sbragaglia, M. & Prosperetti, A. 2007a Effective velocity boundary condition at a mixed slip surface. J. Fluid Mech. 578, 435–451.Google Scholar
Sbragaglia, M. & Prosperetti, A. 2007b A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces. Phys. Fluids 19 (4), 043603.Google Scholar
Scardovelli, R. & Zaleski, S. 2000 Analytical relations connecting linear interfaces and volume fractions in rectangular grids. J. Comput. Phys. 164 (1), 228–237.Google Scholar
Seo, J., Garcia-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783 (2003), 448–473.Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28 (2), 025110.Google Scholar
Seo, J. & Mani, A. 2018 Effect of texture randomization on the slip and interfacial robustness in turbulent flows over superhydrophobic surfaces. Phys. Rev. Fluids 3 (4), 044601.Google Scholar
Srinivasan, S., Kleingartner, J. A., Gilbert, J. B., Cohen, R. E., Milne, A. J. B. & McKinley, G. H. 2015 Sustainable drag reduction in turbulent Taylor–Couette flows by depositing sprayable superhydrophobic surfaces. Phys. Rev. Lett. 114 (1), 2–6.Google Scholar
Türk, S., Daschiel, G., Stroh, A., Hasegawa, Y. & Frohnapfel, B. 2014 Turbulent flow over superhydrophobic surfaces with streamwise grooves. J. Fluid Mech. 747, 186–217.Google Scholar
Vinogradova, O. I. 1995 Drainage of a thin liquid film confined between hydrophobic surfaces. Langmuir 11, 2213–2220.Google Scholar
Wang, L. P., Teo, C. J. & Khoo, B. C. 2014 Effects of interface deformation on flow through microtubes containing superhydrophobic surfaces with longitudinal ribs and grooves. Microfluid Nanofluid 16, 225–236.Google Scholar
Wenzel, R. N. 1936 Resistance of solid surfaces to wetting by water. Ind. Engng Chem. 28 (8), 988–994.Google Scholar
Woolford, B., Prince, J., Maynes, D. & Webb, B. W. 2009 Particle image velocimetry characterization of turbulent channel flow with rib patterned superhydrophobic walls. Phys. Fluids 21 (8), 085106.Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieveing large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.Google Scholar
Yuan, J. & Piomelli, U. 2014 Estimation and prediction of the roughness function on realistic surfaces. J. Turbul. 15 (6), 350–365.Google Scholar
Zhao, J. P., Du, X. D. & Shi, X. h. 2007 Experimental research on friction-reduction with super-hydrophobic surfaces. J. Mar. Sci. Appl. 6, 58–61.Google Scholar