Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T09:19:02.167Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall modes in magnetoconvection at high Hartmann numbers

Published online by Cambridge University Press:  26 June 2018

Wenjun Liu Open the ORCID record for Wenjun Liu [Opens in a new window] ,
Dmitry Krasnov  and
Jörg Schumacher Open the ORCID record for Jörg Schumacher [Opens in a new window]
Wenjun Liu*
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
Dmitry Krasnov
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany
Jörg Schumacher
Affiliation:
Institut für Thermo- und Fluiddynamik, Technische Universität Ilmenau, Postfach 100565, D-98684 Ilmenau, Germany Tandon School of Engineering, New York University, New York, NY 11201, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

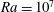Three-dimensional turbulent magnetoconvection at a Rayleigh number of $Ra=10^{7}$ in liquid gallium at a Prandtl number 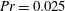$Pr=0.025$ is studied in a closed square cell for very strong external vertical magnetic fields $B_{0}$ in direct numerical simulations which apply the quasistatic approximation. As 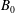$B_{0}$, or equivalently the Hartmann number 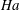$Ha$, are increased, the convection flow, which is highly turbulent in the absence of magnetic fields, crosses the Chandrasekhar linear stability limit for which thermal convection ceases in an infinitely extended layer and which can be assigned a critical Hartmann number 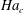$Ha_{c}$. Similar to rotating Rayleigh–Bénard convection, our simulations reveal subcritical sidewall modes that maintain a small but finite convective heat transfer for 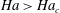$Ha>Ha_{c}$. We report a detailed analysis of the complex two-layer structure of these wall modes, their extension into the cell interior, and a resulting sidewall boundary layer composition that is found to scale with the Shercliff layer thickness.

JFM classification

Boundary Layers: Boundary Layers
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , R2
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aurnou, J. M. & Olson, P. L. 2001 Experiments on Rayleigh–Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.Google Scholar
Burr, U. & Müller, U. 2001 Rayleigh–Bénard convection in liquid metal layers under the influence of a vertical magnetic field. Phys. Fluids 13 (11), 3247–3257.Google Scholar
Busse, F. H. 2008 Asymptotic theory of wall-attached convection in a horizontal fluid layer with a vertical magnetic field. Phys. Fluids 20 (2), 024102.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Cioni, S., Chaumat, S. & Sommeria, J. 2000 Effect of a vertical magnetic field on turbulent Rayleigh–Bénard convection. Phys. Rev. E 62 (4), R4520.Google Scholar
Davidson, P. A. 2016 Introduction to Magnetohydrodynamics. Cambridge University Press.Google Scholar
Ecke, R. E., Zhong, F. & Knobloch, E. 1992 Hopf bifurcation with broken reflection symmetry in rotating Rayleigh–Bénard convection. Europhys. Lett. 19 (3), 177–182.Google Scholar
Fauve, S., Laroche, C. & Libchaber, A. 1981 Effect of a horizontal magnetic field on convective instabilities in mercury. J. Phys. Lett. 42 (21), 455–457.Google Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.Google Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1994 Convection in a rotating cylinder. Part 2. Linear theory for low Prandtl numbers. J. Fluid Mech. 262, 293–324.Google Scholar
Hartmann, J. 1937 Hg-dynamics I: theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15, 1–28.Google Scholar
Horn, S. & Schmid, P. J. 2017 Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection. J. Fluid Mech. 831, 182–211.Google Scholar
Houchens, B. C., Witkowski, L. M. & Walker, J. S. 2002 Rayleigh–Bénard instability in a vertical cylinder with a vertical magnetic field. J. Fluid Mech. 469, 189–207.Google Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.Google Scholar
Knaepen, B. & Moreau, R. 2008 Magnetohydrodynamic turbulence at low magnetic Reynolds number. Annu. Rev. Fluid Mech. 40, 25–45.Google Scholar
Knobloch, E. 1998 Rotating convection: recent developments. Intl J. Engng Sci. 36 (12), 1421–1450.Google Scholar
Krasnov, D., Thess, A., Boeck, T., Zhao, Y. & Zikanov, O. 2013 Patterned turbulence in liquid metal flow: computational reconstruction of the Hartmann experiment. Phys. Rev. Lett. 110, 084501.Google Scholar
Krasnov, D., Zikanov, O. & Boeck, T. 2011 Comparative study of finite difference approaches in simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number. Comput. Fluids 50 (1), 46–59.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Van Heijst, G. J. F. 2013 The structure of sidewall boundary layers in confined rotating Rayleigh–Bénard convection. J. Fluid Mech. 727, 509–532.Google Scholar
Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., Van Heijst, G. J. F. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.Google Scholar
Liu, Y. & Ecke, R. E. 1999 Nonlinear travelling waves in rotating Rayleigh–Bénard convection: stability boundaries and phase diffusion. Phys. Rev. E 59, 4091–4105.Google Scholar
Nakagawa, Y. 1955 An experiment on the inhibition of thermal convection by a magnetic field. Nature 175, 417–419.Google Scholar
Rüdiger, G., Kitchatinov, L. L. & Hollerbach, R. 2013 Magnetic Processes in Astrophysics: Theory, Simulations, Experiments. John Wiley.Google Scholar
Scheel, J. D. & Schumacher, J. 2016 Global and local statistics in turbulent convection at low Prandtl numbers. J. Fluid Mech. 802, 147–173.Google Scholar
Shercliff, J. A. 1953 Steady motion of conducting fluids in pipes under transverse magnetic fields. Math. Proc. Camb. Phil. Soc. 49, 136–144.Google Scholar
Tasaka, Y., Igaki, K., Yanagisawa, T., Vogt, T., Zürner, T. & Eckert, S. 2016 Regular flow reversals in Rayleigh–Bénard convection in a horizontal magnetic field. Phys. Rev. E 93 (4), 043109.Google Scholar
Vasil, G. M., Brummell, N. H. & Julien, K. 2008 A new method for fast transforms in parity-mixed PDEs: Part II. Application to confined rotating convection. J. Comput. Phys. 227 (17), 8017–8034.Google Scholar
Vogt, T., Ishimi, W., Yanagisawa, T., Tasaka, Y., Sakuraba, A. & Eckert, S. 2018 Transition between quasi-two-dimensional and three-dimensional Rayleigh–Bénard convection in a horizontal magnetic field. Phys. Rev. Fluids 3, 013503.Google Scholar
Weiss, N. O. & Proctor, M. R. E. 2014 Magnetoconvection. Cambridge University Press.Google Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1991 Asymmetric modes and transition to vortex structures in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 67, 2473–2476.Google Scholar
Zikanov, O., Krasnov, D., Boeck, T., Thess, A. & Rossi, M. 2014 Laminar-turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 66 (3), 030802.Google Scholar
Zürner, T., Liu, W., Krasnov, D. & Schumacher, J. 2016 Heat and momentum transfer for magnetoconvection in a vertical external magnetic field. Phys. Rev. E 94 (4), 043108.Google Scholar