Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T11:18:24.831Z Has data issue: false hasContentIssue false
  • English
  • Français

The wake structure and transition process of a flow past a sphere affected by a streamwise magnetic field

Published online by Cambridge University Press:  07 March 2018

Jun-Hua Pan ,
Nian-Mei Zhang  and
Ming-Jiu Ni Open the ORCID record for Ming-Jiu Ni [Opens in a new window]
Jun-Hua Pan
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
Nian-Mei Zhang
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
Ming-Jiu Ni*
Affiliation:
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

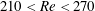The wake structure and transition process of an incompressible viscous fluid flow past a sphere affected by an imposed streamwise magnetic field are investigated numerically over flow regimes that include steady and unsteady laminar flows at Reynolds numbers up to 300. For cases without a magnetic field, a subregion with the existence of a limit cycle is found in the range $210<Re<270$. The point of division is between 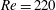$Re=220$ and 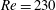$Re=230$. For cases with a streamwise magnetic field, five wake patterns are the steady axisymmetric wake with an attached separation bubble, the steady plane symmetric wake with a small spiral dismissed, the steady plane symmetric wake with a limit cycle, the steady plane symmetric wake with a small spiral fed by the upstream fluid and the unsteady plane symmetric wake with a wave-like oscillation or vortex shedding. Under the influence of an imposed streamwise magnetic field, the wake will be transitioned to various patterns. An interesting ‘reversion phenomenon’, which describes the topological structure behind a sphere with a higher Reynolds number and a certain interaction parameter which corresponds to a lower Reynolds number case with a certain interaction parameter or a much lower Reynolds number case without a magnetic field, is also found. The principal results of the present work are summarized in a map of regimes in the 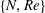$\{N,Re\}$ plane.

JFM classification

Materials Processing Flows: Materials Processing Flows Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 248 - 272
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alemany, A., Moreau, R., Sulem, P. L. & Frisch, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. de Mecanique 28, 2777313.Google Scholar
Branover, H., Eidelman, A. & Nagorny, M. 1995 Use of turbulence modification for heat transfer enhancement in liquid metal blankets. Fusion Engng Des. 27, 719–724.CrossRefGoogle Scholar
Brouillette, E. C. & Lykoudis, P. S. 1967 Magneto-fluid-mechanic channel flow. Part I. Experiment. Phys. Fluids 10 (5), 995–1001.Google Scholar
Chester, W. 1957 The effect of a magnetic field on Stokes flow in a conducting fluid. J. Fluid Mech. 3 (3), 304–308.Google Scholar
Childress, S. 1963 The effect of a strong magnetic field on two-dimensional flows of a conducting fluid. J. Fluid Mech. 15 (3), 429–441.Google Scholar
Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics, vol. 25. Cambridge University Press.Google Scholar
El-Kaddah, N., Patel, A. D. & Natarajan, T. T. 1995 The electromagnetic filtration of molten aluminum using an induced-current separator. JOM Journal of the Minerals, Metals and Materials Society 47 (5), 46–49.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.Google Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20 (5), 051702.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. A. N. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.Google Scholar
Goldsworthy, F. A. 1961 Magnetohydrodynamic flows of a perfectly conducting, viscous fluid. J. Fluid Mech. 11 (4), 519–528.Google Scholar
Hunt, J. C. R. 1965 Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 21 (4), 577–590.CrossRefGoogle Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kalis, Z. E., Tsinober, A. B., Shtern, A. G. & Shcherbinin, E. V. 1965 Flow of conducting fluid past circular cylinder in the presence of transverse magnetic field. Magn. Gidrodin. 1 (1), 18–28.Google Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, S. 2013 Three-dimensional numerical simulations of magnetohydrodynamic flow around a confined circular cylinder under low, moderate, and strong magnetic fields. Phys. Fluids 25 (7), 074102.Google Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three dimensionality in wall-bounded MHD flows. Phys. Rev. Lett. 104 (3), 034502.Google Scholar
Kolesnikov, Y. B. & Tsinober, A. B. 1974 Experimental investigation of two-dimensional turbulence behind a grid. Fluid Dyn. 9 (4), 621–624.CrossRefGoogle Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.Google Scholar
Lahjomri, J., Caperan, P. & Alemany, A. 1993 The cylinder wake in a magnetic field aligned with the velocity. J. Fluid Mech. 253 (253), 421–448.Google Scholar
Lighthill, M. J. 1963 Boundary layer theory. In Laminar Boundary Layers (ed. Rosenhead, L.), pp. 46–103. Oxford University Press.Google Scholar
Magarvey, R. H. & Bishop, R. L. 1961 Transition ranges for three-dimensional wakes. Can. J. Phys. 39 (10), 1418–1422.Google Scholar
Magarvey, R. H. & MacLatchy, C. S. 1965 Vortices in sphere wakes. Can. J. Phys. 43 (9), 1649–1656.Google Scholar
Maxworthy, T. 1962 Measurements of drag and wake structure in magneto-fluid dynamic flow about a sphere. In Heat Transfer and Fluid Mech. Inst, pp. 197–205. Stanford University Press.Google Scholar
Mistrangelo, C. & Bühler, L. 2009 Influence of helium cooling channels on magnetohydrodynamic flows in the HCLL blanket. Fusion Engng Des. 84 (7), 1323–1328.Google Scholar
Mittal, R. 1999 Planar symmetry in the unsteady wake of a sphere. AIAA J. 37 (3), 388–390.Google Scholar
Moreau, R. J. 2013 Magnetohydrodynamics, Springer Science & Business Media.Google Scholar
Mück, B., Günther, C., Müller, U. & Bühler, L. 2000 Three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.Google Scholar
Mutschke, G., Gerbeth, G., Shatrov, V. & Tomboulides, A. 2001 The scenario of three-dimensional instabilities of the cylinder wake in an external magnetic field. Phys. Fluids 13 (3), 723–734.CrossRefGoogle Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Ni, M.-J., Munipalli, R., Huang, P., Morley, N. B. & Abdou, M. A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part II: On an arbitrary collocated mesh. J. Comput. Phys. 227 (1), 205–228.Google Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83 (1), 80–83.Google Scholar
Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME J. Fluids Engng 112, 386–392.Google Scholar
Sekhar, T. V. S., Sivakumar, R. & Kumar, T. R. 2005 Magnetohydrodynamic flow around a sphere. Fluid Dyn. Res. 37 (5), 357–373.CrossRefGoogle Scholar
Shatrov, V., Mutschke, G. & Gerbeth, G. 1997 Numerical simulation of the two-dimensional flow around a circular cylinder. Magnetohydrodynamics 33 (1), 2–10.Google Scholar
Smolentsev, S., Badia, S., Bhattacharyay, R., Bühler, L., Chen, L., Huang, Q., Jin, H.-G., Krasnov, D., Lee, D.-W., de les Valls, E. M. et al. 2015 An approach to verification and validation of MHD codes for fusion applications. Fusion Engng Des. 100, 65–72.Google Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.Google Scholar
Sukoriansky, S., Klaiman, D., Branover, H. & Greenspan, E. 1989 MHD enhancement of heat transfer and its relevance to fusion reactor blanket design. Fusion Engng Des. 8, 277–282.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
Verhille, G., Khalilov, R., Plihon, N., Frick, P. & Pinton, J.-F. 2012 Transition from hydrodynamic turbulence to magnetohydrodynamic turbulence in von Kármán flows. J. Fluid Mech. 693, 243–260.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Yonas, G. 1967 Measurements of drag in a conducting fluid with an aligned field and large interaction parameter. J. Fluid Mech. 30 (4), 813–821.Google Scholar