Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T17:22:46.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake behind a discontinuous cylinder: unveiling the role of the large scales in wake growth and entrainment

Published online by Cambridge University Press:  07 February 2022

V.S.R. Mandava Open the ORCID record for V.S.R. Mandava [Opens in a new window] ,
Joan Herrero ,
Gregory A. Kopp  and
Francesc Giralt Open the ORCID record for Francesc Giralt [Opens in a new window]
V.S.R. Mandava
Affiliation:
Departament d'Enginyeria Química, Universitat Rovira i Virgili, Tarragona, Catalunya43007, Spain
Joan Herrero
Affiliation:
Departament d'Enginyeria Química, Universitat Rovira i Virgili, Tarragona, Catalunya43007, Spain
Gregory A. Kopp
Affiliation:
Boundary Layer Wind Tunnel Laboratory, Faculty of Engineering, University of Western Ontario, London, ONN6A 5B9, Canada
Francesc Giralt*
Affiliation:
Departament d'Enginyeria Química, Universitat Rovira i Virgili, Tarragona, Catalunya43007, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

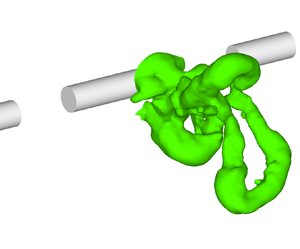
The turbulent flow in the wake of a discontinuous cylinder (DC) was investigated. The DC geometry consisted of cylinder segments $5D$ long (with $D$ being the diameter of the cylinder) separated by gaps of width $2.5D$. Particle image velocimetry and hot-wire anemometry were used to analyse the flow at two Reynolds numbers, $Re = 4000$ and $10\,000$, for $x/D \le 180$. Large eddy simulations for both the DC and the infinite continuous cylinder (CC) wakes were also carried out at $Re = 10\,000$. The DC configuration was devised to trigger the shedding of horseshoe vortices (HSV) in the very-near-wake region with the intent of illustrating the role that these three-dimensional HSVs, previously identified in the far-wake region of CC, play in the entrainment process in turbulent wakes. The DC geometry produced HSVs by the interaction between the high momentum flow through the gaps and the main spanwise vortex shed behind each cylinder segment, while in the CC wake they evolve from near-wake instabilities straddled with hairpin vortices that detach spanwise vorticity from the shed Kármán vortices. The DC wake was found to grow and spread in the transverse direction with a much faster rate than for the CC wake, up until approximately $x/D \approx 50$. Prior to this location, the enhanced growth rate caused by the shear-aligned HSV led to a wake width of approximately 3 times that of the CC wake, with a maximum mean velocity deficit that was approximately half.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 936 , 10 April 2022 , A4
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bailey, S.C.C., Martinuzzi, R.J. & Kopp, G.A. 2002 The effects of wall proximity on vortex shedding from a square cylinder: three-dimensional effects. Phys. Fluids 14 (12), 4160–4177.CrossRefGoogle Scholar
Bisset, D.K., Hunt, J.C.R. & Rogers, M.M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Brown, G.L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
Cao, H.L., Chen, J.G., Zhou, T., Antonia, R.A. & Zhou, Y. 2014 Three-dimensional momentum and heat transport in a turbulent cylinder wake. In 19th Australasian Fluid Mechanics Conference. AFMS.Google Scholar
Chevray, R. 1982 Entrainment interface in free turbulent shear flows. Prog. Energy Combust. Sci. 8, 303–315.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A.L. 1955 Free-stream boundaries of turbulent flows. Technical Rep. TN-1244. NACA.Google Scholar
Dahm, W.J.A. & Dimotakis, P.E. 1987 Measurements of entrainment and mixing in turbulent jets. AIAA J. 25, 1216–1223.CrossRefGoogle Scholar
DaSilva, C.B. & Pereira, J.C.F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.CrossRefGoogle Scholar
Diaz, F., Gavalda, J., Kawall, J.G., Keffer, J.F. & Giralt, F. 1985 Asymmetrical wake generated by a spinning cylinder. AIAA J. 23, 49–54.CrossRefGoogle Scholar
Dimotakis, P.E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
Dol, S.S., Kopp, G.A. & Martinuzzi, R.J. 2008 The suppression of periodic vortex shedding from a rotating circular cylinder. J. Wind Engng Ind. Aerodyn. 96, 1164–1184.CrossRefGoogle Scholar
Dong, S., Karniadakis, G.E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation-particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.CrossRefGoogle Scholar
Ferré, J.A. & Giralt, F. 1989 a Pattern-recognition analysis of the velocity field in plane turbulent wakes. J. Fluid Mech. 198, 27–64.CrossRefGoogle Scholar
Ferré, J.A. & Giralt, F. 1989 b Some topological features of the entrainment process in a heated turbulent wake. J. Fluid Mech. 198, 65–78.CrossRefGoogle Scholar
Ferré, J.A., Mumford, J.C., Savill, A.M. & Giralt, F. 1990 Three-dimensional large-eddy motions and fine-scale activity in a plane turbulent wake. J. Fluid Mech. 210, 371–414.CrossRefGoogle Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W.H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A3 (7), 1760–1765.CrossRefGoogle Scholar
Gerrard, J.H. 1967 Experimental investigation of separated boundary layer undergoing transition to turbulence. Phys. Fluids 10, S98–100.CrossRefGoogle Scholar
Giralt, F. & Ferré, J.A. 1993 Structure and flow patterns in turbulent wakes. Phys. Fluids A5, 1783–1789.CrossRefGoogle Scholar
Grant, H.L. 1958 The large eddies of turbulent motion. J. Fluid Mech. 4, 149–190.CrossRefGoogle Scholar
Hairer, E. & Wanner, G. 1996 Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems, 2nd edn, Springer Series in Computational Mathematics. Springer.CrossRefGoogle Scholar
Hayakawa, M. & Hussain, F. 1989 Three-dimensionality of organized structures in a plane turbulent wake. J. Fluid Mech. 206, 375–404.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19, 071702.CrossRefGoogle Scholar
Hunt, J.C.R., Eames, I., da Silva, C.B. & Westerweel, J. 2011 Interfaces and inhomogeneous turbulence. Phil. Trans. R. Soc. Lond. A 369, 811–832.Google ScholarPubMed
Hunt, J.C.R., Eames, I. & Westerweel, J. 2006 Mechanics of inhomogeneous turbulence and interfacial layers. J. Fluid Mech. 554, 499–519.CrossRefGoogle Scholar
Inoue, O. & Sakuragi, A. 2008 Vortex shedding from a circular cylinder of finite length at low Reynolds numbers. Phys. Fluids 20, 033601.CrossRefGoogle Scholar
Kármán, V. & Rubach, H. 1912 Über den mechanismus des flüssigkeits- und luftwiderstandes. Phys. Z. XIII, Fourty nine-fifty nine.Google Scholar
King, L.V. 1914 On the convection of heat from small cylinders in a stream of fluid: determination of the convection constants of small platinum wires, with applications to hot–wire anemometry. Proc. R. Soc. A 90, 563–570.Google Scholar
Kopp, G.A., Giralt, F. & Keffer, J.F. 2002 Entrainment vortices and interfacial intermittent turbulent bulges in a plane turbulent wake. J. Fluid Mech. 469, 49–70.CrossRefGoogle Scholar
Kopp, G.A., Kawall, J.G. & Keffer, J.F. 1995 The evolution of the coherent structures in a uniformly distorted plane turbulent wake. J. Fluid Mech. 291, 299–322.CrossRefGoogle Scholar
LaRue, J.C. & Libby, P.A. 1974 Temperature and intermittency in the turbulent wake of a heated cylinder. Phys. Fluids 17 (5), 873–878.CrossRefGoogle Scholar
Lilly, D.K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4 (3), 633–635.CrossRefGoogle Scholar
Ma, X., Karamanos, G.S. & Karniadakis, G.E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.CrossRefGoogle Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.CrossRefGoogle Scholar
Mandava, V.S.R., Kopp, G.A., Herrero, J. & Giralt, F. 2009 Experimental investigation of the wake behind a discontinuous cylinder. In Sixth International Symposium on Turbulence and Shear Flow Phenomena (ed. N. Kasagi, F. Rainer, J.A.C. Humphrey & H.J. Sung), vol. 3, pp. 1089–1094.Google Scholar
Martinuzzi, R.J., Bailey, S.C.C. & Kopp, G.A. 2003 Influence of wall proximity on vortex shedding from a square cylinder. Exp. Fluids 34, 585–596.CrossRefGoogle Scholar
Mathew, J. & Basu, A.J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14, 2065–2072.CrossRefGoogle Scholar
McClure, J., Pavan, C. & Yarusevych, S. 2019 Secondary vortex dynamics in the cylinder wake during laminar-to-turbulent transition. Phys. Rev. Fluids 4, 124702.CrossRefGoogle Scholar
Mumford, J.C. 1983 The structure of the large eddies in fully developed turbulent shear flows. Part 2. The plane wake. J. Fluid Mech. 137, 447–456.CrossRefGoogle Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular-cylinder - influence of aspect ratio. J. Fluids Mech. 258, 287–316.CrossRefGoogle Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.CrossRefGoogle Scholar
Ong, L. & Wallace, J. 1996 The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 20, 441–453.CrossRefGoogle Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24, 055108.CrossRefGoogle Scholar
Rhie, C.M. & Chow, W.L. 1983 A numerical study of the turbulent flow past an isolated airfoil with trailing edge separation. AIAA J. 21, 1525–1532.CrossRefGoogle Scholar
Roshko, A. & Fiszdon, W. 1969 On the persistence of transition in the near wake. In SIAM Problems of Hydrodynamics and Continuum Mechanics, pp. 606–616. SIAM.Google Scholar
Sagaut, P. 2001 Large-Eddy Simulation for Incompressible Flows. An Introduction. Springer.CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic equations. Mon. Weath. Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Tang, S.L., Antonia, R.A., Djenidi, L. & Zhou, Y. 2016 Complete self-preservation along the axis of a circular cylinder far wake. J. Fluid Mech. 786, 253–274.CrossRefGoogle Scholar
Taylor, G.J. 1915 Pressure distribution around a cylinder. Tech. Rep. Advisor Committee for Aeronamities.Google Scholar
Taylor, Z.J., Gurka, R. & Kopp, G.A. 2014 Effects of leading-edge geometry on the vortex shedding frequency of an elongated bluff body at high Reynolds number. J. Wind Engng Ind. Aerodyn. 128, 66–75.CrossRefGoogle Scholar
Taylor, Z.J., Palombi, E., Gurka, R. & Kopp, G.A. 2011 Features of the turbulent flow around symmetric elongated bluff bodies. J. Fluids Struct. 27, 250–265.CrossRefGoogle Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the 2nd Midwestern Conference on Fluid Mechanics. pp. 1-19. Ohio State University.Google Scholar
Townsend, A.A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vernet, A. 1999 Private communication.Google Scholar
Vernet, A., Kopp, G.A., Ferré, J.A. & Giralt, F. 1997 Simultaneous velocity and temperature patterns in the far region of a turbulent cylinder wake. J. Fluids Engng 119, 463–466.CrossRefGoogle Scholar
Vernet, A., Kopp, G.A., Ferré, J.A. & Giralt, F. 1999 Three-dimensional structure and momentum transfer in a turbulent cylinder wake. J. Fluid Mech. 394, 303–337.CrossRefGoogle Scholar
Werner, H. & Wengle, H. 1993 Large-eddy simulation of turbulent flow over and around a cube in a plate channel. Selected Papers from the Eighth International Symposium on Turbulent Shear Flows, 1991. In Turbulent Shear Flows (ed. F. Durst et al. ), vol. 8. Springer.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J.M. & Hunt, J.C.R. 2005 Mechanics of the turbulent and non-turbulent interface of a jet. Phys. Rev. Lett. 17, 174501.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J.M. & Hunt, J.C.R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in a cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Yamane, R., Oshima, S., Okubo, M. & Kotani, J. 1988 Coherent structures in the turbulent wake behind a circular cylinder. 3. Flow visualization and hot wire measurements. Fluid Dyn. Res. 4, 47–56.CrossRefGoogle Scholar
Zdravkovich, M.M. 1990 Conceptual over view of laminar and turbulent flows past smooth and rough cylinders. J. Wind Engng Ind. Aerodyn. 33, 53–62.CrossRefGoogle Scholar
Zdravkovich, M.M., Brand, V.P., Mathew, G. & Weston, A. 1989 Flow past short circular cylinders with two free ends. J. Fluid Mech. 203, 557–575.CrossRefGoogle Scholar
Zdravkovich, M.M., Flaherty, A.J., Pahle, M.G. & Skelhorne, I.A. 1998 Some aerodynamic aspects of coin-like cylinders. J. Fluid Mech. 360, 73–84.CrossRefGoogle Scholar