Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T05:22:24.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortical structures in the near wake of tabs with various geometries

Published online by Cambridge University Press:  20 July 2017

A. M. Hamed Open the ORCID record for A. M. Hamed [Opens in a new window] ,
A. Pagan-Vazquez ,
D. Khovalyg ,
Z. Zhang  and
L. P. Chamorro Open the ORCID record for L. P. Chamorro [Opens in a new window]
A. M. Hamed
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
A. Pagan-Vazquez
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
D. Khovalyg
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
Z. Zhang
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
L. P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering Department, University of Illinois, Urbana, IL, 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

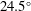The vortical structures and turbulence statistics in the near wake of rectangular, trapezoidal, triangular and ellipsoidal tabs were experimentally studied in a refractive-index-matching channel. The tabs share the same bulk dimensions, including a 17 mm height, a 28 mm base width and a $24.5^{\circ }$ inclination angle. Measurements were performed at two Reynolds numbers based on the tab height, 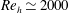$Re_{h}\simeq 2000$ (laminar incoming flow) and 13 000 (turbulent incoming flow). Three-dimensional, three-component particle image velocimetry (PIV) was used to study the mean flow distribution and dominant large-scale vortices, while complementary high-spatial-resolution planar PIV measurements were used to quantify high-order statistics. Instantaneous three-dimensional fields revealed the coexistence of a coherent counter-rotating vortex pair (CVP) and hairpin structures. The CVP and hairpin vortices (the primary structures) exhibit distinctive characteristics and strength across 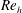$Re_{h}$ and tab geometries. The CVP is coherently present in the mean flow field and grows in strength over a significantly longer distance at the low 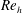$Re_{h}$ due to the lower turbulence levels and the delayed shedding of the hairpin vortices. These features at the low $Re_{h}$ are associated with the presence of Kelvin–Helmholtz instability that develops over three tab heights downstream of the trailing edge. Moreover, a secondary CVP with an opposite sense of rotation resides below the primary one for the four tabs at the low 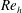$Re_{h}$. The interaction between the hairpin structures and the primary CVP is experimentally measured in three dimensions and shows complex coexistence. Although the CVP undergoes deformation and splitting at times, it maintains its presence and leads to significant mean spanwise and wall-normal flows.

JFM classification

Vortex Flows: Vortex Flows Vortex Flows: Vortex interactions Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 167 - 188
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bai, K. & Katz, J. 2014 On the refractive index of sodium iodide solutions for index matching in piv. Exp. Fluids 55, 1–6.CrossRefGoogle Scholar
Blois, G., Christensen, K. T., Best, J. L., Elliott, G., Austin, J., Dutton, C., Bragg, M., Garcia, M. & Fouke, B. 2012 A versatile refractive-index-matched flow facility for studies of complex flow systems across scientific disciplines. In 50th American Institute of Aeronautics and Astronautics (AIAA) Aerospace Sciences Meeting, Nashville, TN, AIAA, AIAA 2012-0736, doi:10.2514/6.2012-736.Google Scholar
Calderon, D. E., Wang, Z., Gursul, I. & Visbal, M. R. 2013 Volumetric measurements and simulations of the vortex structures generated by low aspect ratio plunging wings. Phys. Fluids 25 (6), 067102.Google Scholar
Cambonie, T., Gautier, N. & Aider, J.-L. 2013 Experimental study of counter-rotating vortex pair trajectories induced by a round jet in cross-flow at low velocity ratios. Exp. Fluids 54 (3), 1–13.Google Scholar
Chamorro, L. P., Troolin, D. R., Lee, S., Arndt, R. E. A. & Sotiropoulos, F. 2013 Three-dimensional flow visualization in the wake of a miniature axial-flow hydrokinetic turbine. Exp. Fluids 54 (2), 1–12.Google Scholar
Cheng, B., Sane, S. P., Barbera, G., Troolin, D. R., Strand, T. & Deng, X. 2013 Three-dimensional flow visualization and vorticity dynamics in revolving wings. Exp. Fluids 54 (1), 1–12.Google Scholar
Chua, L., Yu, S. & Wang, X. 2003 Flow visualization and measurements of a square jet with mixing tabs. Exp. Therm. Fluid Sci. 27 (6), 731–744.CrossRefGoogle Scholar
Dong, S. & Meng, H. 2004 Flow past a trapezoidal tab. J. Fluid. Mech. 510, 219–242.CrossRefGoogle Scholar
Elavarasan, R. & Meng, H. 2000 Flow visualization study of role of coherent structures in a tab wake. Fluid Dyn. Res. 27 (3), 183–197.CrossRefGoogle Scholar
Gad-elhak, M. 2000 Flow Control: Passive, Active and Reactive Flow Management. Cambridge University Press.CrossRefGoogle Scholar
Ghanem, A., Habchi, C., Lemenand, T., Della Valle, D. & Peerhossaini, H. 2013 Energy efficiency in process industry – high-efficiency vortex (HEV) multifunctional heat exchanger. J. Renew. Energy 56, 96–104.Google Scholar
Ghanem, A., Lemenand, T., Della Valle, D., Habchi, C. & Peerhossaini, H. 2012 Vortically enhanced heat transfer and mixing: state of the art and recent results. In ASME 2012 Heat Transfer Summer Conference, pp. 21–30. American Society of Mechanical Engineers.Google Scholar
Gretta, W. J.1990 An exsperimental study of the fluid mixing effects and flow structure due to surface mounted passive vortex generating device. Master’s thesis, Lehigh University, Bethlehem, PA, USA.Google Scholar
Gretta, W. J. & Smith, C. R. 1993 Flow structure and statistics of a passive mixing tab. Trans. ASME 115 (2), 255–263.Google Scholar
Habchi, C., Lemenand, T., Della Valle, D. & Peerhossaini, H. 2010a Alternating mixing tabs in multifunctional heat exchanger-reactor. Chem. Engng Process. 49 (7), 653–661.CrossRefGoogle Scholar
Habchi, C., Lemenand, T., Valle, D. & Peerhossaini, H. 2010b Turbulence behavior of artificially generated vorticity. J. Turbul. 11 (36), 1–28.CrossRefGoogle Scholar
Hamed, A. M., Kamdar, A., Castillo, L. & Chamorro, L. P. 2015 Turbulent boundary layer over 2D and 3D large-scale wavy walls. Phys. Fluids 27 (10), 106601.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88, p. 193.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kaci, H. M., Habchi, C., Lemenand, T., Della Valle, D. & Peerhossaini, H. 2010 Flow structure and heat transfer induced by embedded vorticity. Intl J. Heat Mass Transfer 53 (17), 3575–3584.Google Scholar
Lögdberg, O., Fransson, J. H. M. & Alfredsson, P. H. 2009 Streamwise evolution of longitudinal vortices in a turbulent boundary layer. J. Fluid Mech. 623, 27–58.Google Scholar
Moriconi, L. 2009 Minimalist turbulent boundary layer model. Phys. Rev. E 79 (4), 046306.Google ScholarPubMed
Park, J., Pagan-Vazquez, A., Alvarado, J. L., Chamorro, L. P., Lux, S. & Marsh, C. 2016 Experimental and numerical visualization of counter rotating vortices. J. Heat Transfer 138 (8), 080908.CrossRefGoogle Scholar
Pereira, F. & Gharib, M. 2002 Defocusing digital particle image velocimetry and the three-dimensional characterization of two-phase flows. Meas. Sci. Tech. 13, 683–694.CrossRefGoogle Scholar
Pereira, F., Gharib, M., Dabiri, D. & Modarress, D. 2000 Defocusing digital particle image velocimetry: a 3-component 3-dimensional DPIV measurement technique. Application to bubbly flows. Exp. Fluids 29, S078–S084.CrossRefGoogle Scholar
Reeder, M. & Samimy, M. 1996 The evolution of a jet with vortex-generating tabs: real-time visualization and quantitative measurements. J. Fluid Mech. 311, 73–118.Google Scholar
Sharp, K., Hill, D., Troolin, D., Walters, G. & Lai, W. 2010 Volumetric 3-component velocimetry measurements of the turbulent flow around a Rushton turbine. Exp. Fluids 48 (1), 167–183.CrossRefGoogle Scholar
Stephens, A. V. & Collins, G. A.1955 Turbulent boundary layer control by ramps or wedges. Australian Aeronautical Research Committee – Report p. 19.Google Scholar
Sun, Z., Schrijer, F. F. J., Scarano, F. & Van Oudheusden, B. W. 2012 The three-dimensional flow organization past a micro-ramp in a supersonic boundary layer. Phys. Fluids 24 (5), 055105.CrossRefGoogle Scholar
Troolin, D. & Longmire, E. K. 2009 Volumetric velocity measurements of vortex rings from inclined exits. Exp. Fluids 48 (3), 409–420.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568 (1), 55–76.Google Scholar
Yang, W., Meng, H. & Sheng, J. 2001 Dynamics of hairpin vortices generated by a mixing tab in a channel flow. Exp. Fluids 30 (6), 705–722.Google Scholar
Ye, Q., Schrijer, F. F. J. & Scarano, F. 2016 Boundary layer transition mechanisms behind a micro-ramp. J. Fluid Mech. 793, 132–161.CrossRefGoogle Scholar
Yu, Y., Zhang, J. & Shan, Y. 2015 Convective heat transfer of a row of air jets impingement excited by triangular tabs in a confined crossflow channel. Intl J. Heat Mass Transfer 80, 126–138.Google Scholar
Zaman, K., Reeder, M. & Samimy, M. 1994 Control of an axisymmetric jet using vortex generators. Phys. Fluids 6 (2), 778–793.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar