Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T13:49:35.465Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibrations of a flexible cylinder at subcritical Reynolds number

Published online by Cambridge University Press:  04 September 2020

Rémi Bourguet Open the ORCID record for Rémi Bourguet [Opens in a new window]
Rémi Bourguet*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse and CNRS, Toulouse31400, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow past a fixed rigid cylinder becomes unsteady beyond a critical Reynolds number close to $47$, based on the body diameter and inflow velocity. The present paper explores numerically the vortex-induced vibrations (VIV) that may develop for a flexible cylinder at subcritical Reynolds number ($Re$), i.e. for $Re<47$. Flexible-cylinder VIV are found to occur down to $Re\approx 20$, as previously reported for elastically mounted rigid cylinders. A detailed analysis is carried out for $Re=25$, in two steps: the system behaviour is examined from the emergence of VIV to the excitation of the first structural modes; and then focus is placed on higher-mode responses. In all cases, a single vibration frequency is excited in each direction. 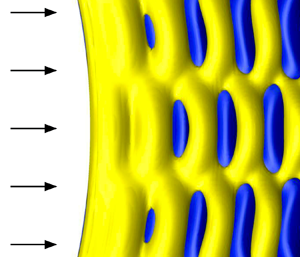The cross-flow and in-line responses exhibit contrasting magnitudes (peak amplitudes of $0.35$ versus $0.01$ diameters), as well as distinct symmetry properties and evolutions (e.g. standing/travelling waves). The flow, unsteady once the cylinder vibrates, is found to be temporally and spatially locked with body motion. The synchronization with the cross-flow standing-wave responses is accompanied by the formation of cellular wake patterns, regardless of the modes involved in the vibrations. Body trajectory varies along the span, but dominant orbits can be identified. Despite the low amplitudes of the in-line responses, connections are uncovered between orbit orientation and flow–structure energy transfer, with different trends in each direction.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 902 , 10 November 2020 , R3
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2011 Vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 677, 342–382.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2013 Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 717, 361–375.CrossRefGoogle Scholar
Buffoni, E. 2003 Vortex shedding in subcritical conditions. Phys. Fluids 15, 814–816.CrossRefGoogle Scholar
Chaplin, J. R., Bearman, P. W., Huera-Huarte, F. J. & Pattenden, R. J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21, 3–24.CrossRefGoogle Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14, 183–196.CrossRefGoogle Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S. & Oakley, O. H. 2010 Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 643, 395–424.CrossRefGoogle Scholar
Dolci, D. I. & Carmo, B. S. 2019 Bifurcation analysis of the primary instability in the flow around a flexibly mounted circular cylinder. J. Fluid Mech. 880, 1–11.CrossRefGoogle Scholar
Fan, D., Wang, Z., Triantafyllou, M. S. & Karniadakis, G. E. 2019 Mapping the properties of the vortex-induced vibrations of flexible cylinders in uniform oncoming flow. J. Fluid Mech. 881, 815–858.CrossRefGoogle Scholar
Gedikli, E. D., Chelidze, D. & Dahl, J. M. 2018 Observed mode shape effects on the vortex-induced vibration of bending dominated flexible cylinders simply supported at both ends. J. Fluids Struct. 81, 399–417.CrossRefGoogle Scholar
Huera-Huarte, F. J., Bangash, Z. A. & González, L. M. 2014 Towing tank experiments on the vortex-induced vibrations of low mass ratio long flexible cylinders. J. Fluids Struct. 48, 81–92.CrossRefGoogle Scholar
Karniadakis, G. E. & Sherwin, S. 1999 Spectral/hp Element Methods for CFD, 1st edn.Oxford University Press.Google Scholar
Kou, J., Zhang, W., Liu, Y. & Li, X. 2017 The lowest Reynolds number of vortex-induced vibrations. Phys. Fluids 29, 041701.CrossRefGoogle Scholar
Mathis, C., Provansal, M. & Boyer, L. 1984 The Bénard-von Kármán instability: an experimental study near the threshold. J. Phys. Lett. 45, 483–491.CrossRefGoogle Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re. J. Fluid Mech. 534, 185–194.CrossRefGoogle Scholar
Newman, D. J. & Karniadakis, G. E. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Edraki, M. & Modarres-Sadeghi, Y. 2019 Effects of boundary conditions on vortex-induced vibration of a fully submerged flexible cylinder. Exp. Fluids 60, 1–14.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Wu, X., Ge, F. & Hong, Y. 2012 A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 28, 292–308.CrossRefGoogle Scholar