Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T14:18:24.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibration of a sphere close to or piercing a free surface

Published online by Cambridge University Press:  04 November 2021

Methma M. Rajamuni Open the ORCID record for Methma M. Rajamuni [Opens in a new window] ,
Kerry Hourigan  and
Mark C. Thompson
Methma M. Rajamuni*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia School of Engineering and Information Technology, University of New South Wales Canberra, Northcott Dr, Campbell, ACT 2612, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

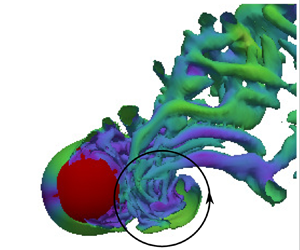
Vortex-induced vibration (VIV) of an elastically mounted sphere placed close to or piercing a free surface (FS) was investigated numerically. The submergence depth ($h$) was systematically varied between $1$ and $-$0.75 sphere diameters ($D$) and the response simulated over the reduced velocity range $U^*\in [3.5,14]$. The incompressible flow was coupled with the sphere motion modelled by a spring–mass–damper system, treating the free-surface boundary as a slip wall. In line with the previous experimental findings, as the submergence depth was decreased from $h^* = h/D =1$, the maximum response amplitude of the fully submerged sphere decreased; however, as the sphere pierced the FS, the amplitude increased until $h^* = -0.375$, and then decreased beyond that point. The fluctuating components of the lift and drag coefficients also followed the same pattern. The variation of the near-wake vortex dynamics over this submergence range was examined in detail to understand the effects of $h^*$ on the VIV response. It was found that $h^* = 1$ is a critical submergence depth, beyond which, as $h^*$ is decreased, the vortical structures in the wake vary significantly. For a fully submerged sphere, the influence of the stress-free condition on the VIV response was dominant over the kinematic constraint preventing flow through the surface. For piercing sphere cases, two previously unseen vortical recirculations were formed behind the sphere near times of maximal displacement, enhancing the VIV response. These were strongest at $h^* = -0.375$, and much weaker for small submergence depths, explaining the observed response-amplitude variation.

JFM classification

Aerodynamics: Flow-structure interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 929 , 25 December 2021 , A41
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barbosa, J.M.O., Qu, Y., Metrikine, A.V. & Lourens, E. 2017 Vortex-induced vibrations of a freely vibrating cylinder near a plane boundary: experimental investigation and theoretical modelling. J. Fluids Struct. 69, 382–401.CrossRefGoogle Scholar
Behara, S., Borazjani, I. & Sotiropoulos, F. 2011 Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at $Re = 300$: hysteresis and vortex shedding modes. J. Fluid Mech. 686, 426–450.CrossRefGoogle Scholar
Behara, S. & Sotiropoulos, F. 2016 Vortex-induced vibrations of an elastically mounted sphere: the effects of Reynolds number and reduced velocity. J. Fluids Struct. 66, 54–68.CrossRefGoogle Scholar
Bernal, L.P. & Kwon, J.T. 1989 Vortex ring dynamics at a free surface. Phys. Fluids A: Fluid Dyn. 1 (3), 449–451.CrossRefGoogle Scholar
Blackburn, H. & Henderson, R. 1996 Lock-in behavior in simulated vortex-induced vibration. Exp. Therm. Fluid Sci. 12 (2), 184–189.CrossRefGoogle Scholar
Campagne, G, Cazalbou, J.B., Joly, L. & Chassaing, P. 2009 The structure of a statistically steady turbulent boundary layer near a free-slip surface. Phys. Fluids 21 (6), 065111.CrossRefGoogle Scholar
Chizfahm, A., Joshi, V. & Jaiman, R. 2021 Transverse flow-induced vibrations of a sphere in the proximity of a free surface: a numerical study. J. Fluids Struct. 101, 103224.CrossRefGoogle Scholar
Chung, M. 2016 Two-degree-of-freedom vortex induced vibration of low-mass horizontal circular cylinder near a free surface at low Reynolds number. Intl J. Heat Fluid Flow 57, 58–78.CrossRefGoogle Scholar
Doğan, S., Özgören, M., Okbaz, A., Şahin, B. & Akıllı, H. 2018 Investigation of interactions between a sphere wake and free surface. J. Fac. Engng Arch. Gazi Univ. 33 (3), 1123–1133.Google Scholar
Gharib, M. & Weigand, A. 1996 Experimental studies of vortex disconnection and connection at a free surface. J. Fluid Mech. 321, 59–86.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 1997 Vortex-induced motions of a tethered sphere. J. Wind Engng Ind. Aerodyn. 69, 375–385.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Govardhan, R.N. & Williamson, C.H.K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.CrossRefGoogle Scholar
Hassanzadeh, R., Sahin, B. & Ozgoren, M. 2012 Large eddy simulation of free–surface effects on the wake structures downstream of a spherical body. Ocean Engng 54, 213–222.CrossRefGoogle Scholar
Issa, R.I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62 (1), 40–65.CrossRefGoogle Scholar
Jauvtis, N., Govardhan, R. & Williamson, C.H.K. 2001 Multiple modes of vortex-induced vibration of a sphere. J. Fluids Struct. 15 (3), 555–563.CrossRefGoogle Scholar
Kawamura, T., Mayer, S., Garapon, A. & Sørensen, L. 2002 Large eddy simulation of a flow past a free surface piercing circular cylinder. Trans. ASME J. Fluids Engng 124 (1), 91–101.CrossRefGoogle Scholar
Leontini, J.S., Lo Jacono, D. & Thompson, M.C. 2013 Wake states and frequency selection of a streamwise oscillating cylinder. J. Fluid Mech. 730, 162–192.CrossRefGoogle Scholar
Leontini, J.S., Thompson, M.C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22 (6), 857–864.CrossRefGoogle Scholar
Lighthill, J. 1986 Wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
Mirauda, D., Plantamura, A.V. & Malavasi, S. 2014 Dynamic response of a sphere immersed in a shallow water flow. Trans. ASME J. Offshore Mech. Arctic Engng 136 (2), 021101.CrossRefGoogle Scholar
Ohring, S. & Lugt, H.J. 1991 Interaction of a viscous vortex pair with a free surface. J. Fluid Mech. 227, 47–70.CrossRefGoogle Scholar
Ozgoren, M., Canli, E., Dogan, S.A., Sahin, B. & Akilli, H. 2013 a Experimental determination of effects of free surface and its interaction with sphere wake flow for an inline two spheres. In 8th World Conference on Experimental Heat Transfer, Fluid Mechanics, and Thermodynamics, pp. 16–20.Google Scholar
Ozgoren, M., Dogan, S., Okbaz, A., Aksoy, M.H., Sahin, B. & Akıllı, H. 2013 b Comparison of flow characteristics of different sphere geometries under the free surface effect. In EPJ Web of Conferences, vol. 45, p. 01022. EDP Sciences.CrossRefGoogle Scholar
Ozgoren, M., Dogan, S., Okbaz, A., Sahin, B. & Akilli, H. 2012 Passive control of flow structure interaction between a sphere and free-surface. In EPJ Web of Conferences, vol. 25, p. 01065. EDP Sciences.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2016 Vortex-induced vibration of rotating spheres. In 20th Australasian Fluid Mechanics Conference Perth, Australia, The University of Melbourne.Google Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2018 a Transverse flow-induced vibrations of a sphere. J. Fluid Mech. 837, 931–966.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2018 b Vortex-induced vibration of a transversely rotating sphere. J. Fluid Mech. 847, 786–820.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2019 Vortex-induced vibration of elastically-mounted spheres: a comparison of the response of three degrees of freedom and one degree of freedom systems. J. Fluids Struct. 89, 142–155.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2020 a Efficient FSI solvers for multiple-degrees-of-freedom flow-induced vibration of a rigid body. Comput. Fluids 196, 104340.CrossRefGoogle Scholar
Rajamuni, M.M., Thompson, M.C. & Hourigan, K. 2020 b Vortex dynamics and vibration modes of a tethered sphere. J. Fluid Mech. 885, A10.CrossRefGoogle Scholar
Rajamuni, R.D.M.M. 2018 Flow-induced vibration of a spherical body. PhD thesis, Monash University.Google Scholar
Reichl, P., Hourigan, K. & Thompson, M.C. 2005 Flow past a cylinder close to a free surface. J. Fluid Mech. 533, 269–296.CrossRefGoogle Scholar
Saelim, N. 1999 Self-excited oscillations of a horizontal cylinder adjacent to a free-surface. Masters of Science thesis, Lehigh University.Google Scholar
Sareen, A., Zhao, J., Sheridan, J., Hourigan, K. & Thompson, M.C. 2018 Vortex-induced vibrations of a sphere close to a free surface. J. Fluid Mech. 846, 1023–1058.CrossRefGoogle Scholar
Sheridan, J., Lin, J.C. & Rockwell, D. 1995 Metastable states of a cylinder wake adjacent to a free surface. Phys. Fluids 7 (9), 2099–2101.CrossRefGoogle Scholar
Sheridan, J., Lin, J.C. & Rockwell, D. 1997 Flow past a cylinder close to a free surface. J. Fluid Mech. 330, 1–30.CrossRefGoogle Scholar
Williamson, C.H.K. & Govardhan, R. 1997 Dynamics and forcing of a tethered sphere in a fluid flow. J. Fluids Struct. 11 (3), 293–305.CrossRefGoogle Scholar
Yu, G., Avital, E.J. & Williams, J.J.R. 2008 Large eddy simulation of flow past free surface piercing circular cylinders. Trans. ASME J. Fluids Engng 130 (10), 101304.CrossRefGoogle Scholar
Zhang, C., Shen, L. & Yue, D.K.P. 1999 The mechanism of vortex connection at a free surface. J. Fluid Mech. 384, 207–241.CrossRefGoogle Scholar

Rajamuni et al. supplementary movie 1

movie1-fr-hs1-u9.avi

Download Rajamuni et al. supplementary movie 1(Video)
Video 1.3 MB

Rajamuni et al. supplementary movie 2

movie2-fr-hs0.0625-u9.avi

Download Rajamuni et al. supplementary movie 2(Video)
Video 1.1 MB

Rajamuni et al. supplementary movie 3

movie3-fr-hs-0.0125-u9.avi

Download Rajamuni et al. supplementary movie 3(Video)
Video 1.5 MB

Rajamuni et al. supplementary movie 4

movie4-fr-hs-0.375-u9.avi
Download Rajamuni et al. supplementary movie 4(Video)
Video 1.9 MB

Rajamuni et al. supplementary movie 5

movie5-fs-hs-0.625-u9.avi
Download Rajamuni et al. supplementary movie 5(Video)
Video 1.2 MB

Rajamuni et al. supplementary movie 6

movie6-fr-hs-0.375-u8.avi
Download Rajamuni et al. supplementary movie 6(Video)
Video 1.5 MB