Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T15:18:29.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibration of a neutrally buoyant tethered sphere

Published online by Cambridge University Press:  19 February 2013

H. Lee ,
K. Hourigan  and
M. C. Thompson
H. Lee
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia Division of Biological Engineering, Monash University, Melbourne, VIC 3800, Australia
M. C. Thompson*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A combined numerical and experimental study examining vortex-induced vibration (VIV) of a neutrally buoyant tethered sphere has been undertaken. The study covered the Reynolds-number range 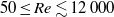$50\leq \mathit{Re}\lesssim 12\hspace{0.167em} 000$, with the numerical (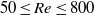$50\leq \mathit{Re}\leq 800$) and experimental (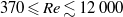$370\leqslant \mathit{Re}\lesssim 12\hspace{0.167em} 000$) ranges overlapping. Neutral buoyancy was chosen to eliminate one parameter, i.e. the influence of gravity, on the VIV behaviour, although, of course, the effect of added mass remains. The tether length was also chosen to be sufficiently long so that, to a good approximation, the sphere was constrained to move within a plane. Seven broad but relatively distinct sphere oscillation and wake states could be distinguished. For regime I, the wake is steady and axisymmetric, and it undergoes transition to a steady two-tailed wake in regime II at 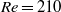$\mathit{Re}= 210$. Those regimes are directly analogous to those of a fixed sphere. Once the sphere begins to vibrate at 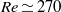$\mathit{Re}\simeq 270$ in regime III, the wake behaviour is distinct from the fixed-sphere wake. Initially the vibration frequency of the sphere is half the shedding frequency in the wake, with the latter consistent with the fixed-sphere wake frequency. The sphere vibration is not purely periodic but modulated over several base periods. However, at slightly higher Reynolds numbers (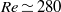$\mathit{Re}\simeq 280$), planar symmetry is broken, and the vibration shifts to the planar normal (or azimuthal) direction, and becomes completely azimuthal at the start of regime IV at 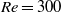$\mathit{Re}= 300$. In comparison, for a fixed sphere, planar symmetry is broken at a much higher Reynolds number of 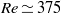$\mathit{Re}\simeq 375$. Interestingly, planar symmetry returns to the wake for 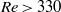$\mathit{Re}\gt 330$, in regime V, for which the oscillations are again radial, and is maintained until 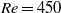$\mathit{Re}= 450$ or higher. At the same time, the characteristic vortex loops in the wake become symmetrical, i.e. two-sided. For 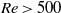$\mathit{Re}\gt 500$, in regime VI, the trajectory of the sphere becomes irregular, possibly chaotic. That state is maintained over the remaining Reynolds-number range simulated numerically (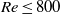$\mathit{Re}\leq 800$). Experiments overlapping this Reynolds-number range confirm the amplitude radial oscillations in regime V and the chaotic wandering for regime VI. At still higher Reynolds numbers of 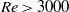$\mathit{Re}\gt 3000$, in regime VII, the trajectories evolve to quasi-circular orbits about the neutral point, with the orbital radius increasing as the Reynolds number is increased. At $\mathit{Re}= 12\hspace{0.167em} 000$, the orbital diameter reaches approximately one sphere diameter. Of interest, this transition sequence is distinct from that for a vertically tethered heavy sphere, which undergoes transition to quasi-circular orbits beyond 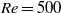$\mathit{Re}= 500$.

JFM classification

Aerodynamics: Aerodynamics Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 97 - 128
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Behara, S., Borazjani, I. & Sotiropoulos, F. 2011 Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at $\mathit{Re}= 300$ : hysteresis and vortex shedding modes. J. Fluid Mech. 686, 426–450.Google Scholar
Bishop, R. E. D & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A 277, 51–75.Google Scholar
Blackburn, H. M. & Henderson, R. D. 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.Google Scholar
Brücker, C. 2001 Spatio-temporal reconstruction of vortex dynamics in axisymmetric wakes. J. Fluids Struct. 15, 543–554.Google Scholar
Carberry, J., Govardhan, R., Sheridan, J., Rockwell, D. & Williamson, C. H. K. 2004 Wake states and response branches of forced and freely oscillating cylinders. Eur. J. Mech. (B/Fluids) 23, 89–97.Google Scholar
Chomaz, J. M., Bonneton, P. & Hopfinger, E. J. 1993 The structure of the near wake of a sphere moving horizontally in a stratified field. J. Fluid Mech. 254, 1–21.Google Scholar
Dennis, S. C. R. & Walker, J. D. A. 1971 Calculation of the steady flow past a sphere at low and moderate Reynolds numbers. J. Fluid Mech. 48, 771–789.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.Google Scholar
Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications. SIAM.CrossRefGoogle Scholar
Gottlieb, O. 1997 Bifurcations of a nonlinear small-body ocean-mooring system excited by finite-amplitude waves. Trans. ASME: J. Offshore Mech. Arctic Engng 119, 234–238.Google Scholar
Govardhan, R. & Williamson, C. H. K. 1997 Vortex-induced motions of a tethered sphere. J. Wind Engng Ind. Aerodyn. 69–71, 375–385.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1982 Some recent studies of vortex shedding with application to marine tubulars and risers. Trans. ASME: J. Energy Resour. Technol. 104, 2–13.Google Scholar
Harlemann, D. & Shapiro, W. 1961 The dynamics of a submerged moored sphere in oscillatory waves. Coast. Engng J. 2, 746–765.Google Scholar
Jauvtis, N., Govardhan, R. & Williamson, C. H. K. 2001 Multiple modes of vortex-induced vibrations of a sphere. J. Fluids Struct. 15, 555–563.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods of the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 31 (11), 3260–3265.Google Scholar
Lee, H., Thompson, M. C. & Hourigan, K. 2008 Vortex-induced vibrations of a tethered sphere with neutral buoyancy. In Proceedings of the XXIIth International Congress on Theoretical and Applied Mechanics (ICTAM 2008), Adelaide, Australia, p. 11299.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.CrossRefGoogle Scholar
Leweke, T., Provansal, M., Ormières, D. & Lebescond, R. 1999 Vortex dynamics in the wake of a sphere. Phys. Fluids 11 (9), S12.Google Scholar
Leweke, T., Thompson, M. C. & Hourigan, K. 2006 Instability of the flow around an impacting sphere. J. Fluid Struct. 22 (6), 961–971.Google Scholar
Magarvey, R. H. & Bishop, R. L. 1961a Transition ranges for three-dimensional wakes. Can. J. Phys. 39, 1418–1422.Google Scholar
Magarvey, R. H. & Bishop, R. L. 1961b Wakes in liquid–liquid systems. Phys. Fluids 4, 800–805.Google Scholar
Mittal, R. 1999a A Fourier–Chebyshev spectral collocation method for simulating flow past spheres and spheroids. Intl J. Numer. Meth. Fluids 30, 921–937.Google Scholar
Mittal, R. 1999b Planar symmetry in the unsteady wake of a sphere. AIAA J. 37, 388–390.Google Scholar
Morison, J. R., O’Brien, M. P., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. Petrol. Trans. AIME 189, 149–157.Google Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83, 80–83.Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 The instability in the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.CrossRefGoogle Scholar
Pregnalato, C. J. 2003 The flow-induced vibrations of a tethered sphere. PhD thesis, Monash University, Melbourne, Australia.Google Scholar
Provansal, M., Schouveiler, L. & Leweke, T. 2004 From the double vortex street behind a cylinder to the the wakes of a sphere. Eur. J. Mech. (B/Fluids) 23, 65–80.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2007 The effect of mass ratio and tether length on the flow around a tethered cylinder. J. Fluid Mech. 591, 117–144.Google Scholar
Sarpkaya, T. 1979 Vortex-induced oscillations. Trans. ASME: J. Appl. Mech. 46, 241–258.Google Scholar
Sarpkaya, T. 1986 Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 165, 61–71.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Schouveiler, L. & Provansal, M. 2002 Self-sustained oscillations in the wake of a sphere. Phys. Fluids 14, 3846–3854.Google Scholar
Shi-Igai, H. & Kono, T. 1969 Study on vibration of submerged spheres caused by surface waves. Coast. Engng Japan 12, 29–40.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 Numerical and experimental studies of the rolling sphere wake. J. Fluid Mech. 643, 137–162.Google Scholar
Taneda, S. 1956 Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Japan 11, 302–307.Google Scholar
Thompson, M. C. & Hourigan, K. 2005 The shear layer instability of a circular cylinder wake. Phys. Fluids 17 (2), 021702.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30 (11), 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C., Leweke, T. & Hourigan, K. 2007 Sphere–wall collision: vortex dynamics and stability. J. Fluid Mech. 575, 121–148.Google Scholar
Thompson, M. C., Leweke, T. & Provansal, M. 2001 Kinematics and dynamics of sphere wake transition. J. Fluids Struct. 15, 575–585.CrossRefGoogle Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
Tomboulides, A. G., Orszag, S. A. & Karniadakis, G. E. 1993 Direct and large-eddy simulation of axisymmetric wakes. AIAA Paper 93-0546..Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. & Govardhan, R. 1997 Dynamics and forcing of a tethered sphere in a fluid flow. J. Fluids Struct. 11, 293–305.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar