Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T06:29:33.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-dipole collapse induced by droplet inertia and phase change

Published online by Cambridge University Press:  26 October 2017

S. Ravichandran Open the ORCID record for S. Ravichandran [Opens in a new window]  and
Rama Govindarajan
S. Ravichandran*
Affiliation:
TIFR Centre for Interdisciplinary Sciences, Narsingi, Hyderabad 500075, India Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore 560064, India
Rama Govindarajan
Affiliation:
International Centre for Theoretical Sciences, Shivakote, Bangalore 560089, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Droplet-laden flows with phase change are common. This study brings to light a mechanism by which droplet inertial dynamics and local phase change, taking place at sub-Kolmogorov scales, affect vortex dynamics in the inertial range of turbulence. To do this we consider vortices placed in a supersaturated ambient initially at constant temperature, homogeneous vapour concentration and uniformly distributed droplets. The droplets also act as sites of phase change. This allows the time scales associated with particle inertia and phase change, which could be significantly different from each other and from the time scale of the flow, to become coupled, and for their combined dynamics to govern the flow. The thermodynamics of condensation and evaporation have a characteristic time scale 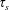$\unicode[STIX]{x1D70F}_{s}$. The water droplets are treated as Stokesian inertial particles with a characteristic time scale 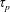$\unicode[STIX]{x1D70F}_{p}$, whose behaviour we approximate using an 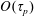$O(\unicode[STIX]{x1D70F}_{p})$ truncation of the Maxey–Riley equation for heavy particles. This inertia leads the water droplets to vacate the vicinity of vortices, leaving no nuclei for the vapour to condense. The condensation process is thus spatially inhomogeneous, and leaves vortices in the flow colder than their surroundings. The combination of buoyancy and vorticity generates a lift force on the vortices perpendicular to their velocity relative to the fluid around them. In the case of a vortex dipole, this lift force can propel the vortices towards each other and undergo collapse, a phenomenon studied by Ravichandran et al. (Phys. Rev. Fluids, vol. 2, 2017, 034702). We find, spanning the space of the two time scales, 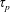$\unicode[STIX]{x1D70F}_{p}$ and 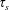$\unicode[STIX]{x1D70F}_{s}$, the region in which lift-induced dipole collapse can occur, and show numerically that the product of the time scales is the determining parameter. Our findings agree with our results from scaling arguments. We also study the influence of varying the initial supersaturation, and find that the strength of the lift-induced mechanism has a power-law dependence on the phase-change time scale 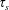$\unicode[STIX]{x1D70F}_{s}$. We then study systems of many vortices and show that the same coupling between the two time scales alters the dynamics of such systems, by energising the smaller scales. We show that this effect is significantly more pronounced at higher Reynolds numbers. Finally, we discuss how this effect could be relevant in conditions typical of clouds.

JFM classification

Phase change: Condensation/evaporation Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 745 - 776
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bohren, C. F. & Albrecht, B. A. 2000 Atmospheric Thermodynamics. AAPT.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18 (2), 027102.Google Scholar
Dixit, H. N. & Govindarajan, R. 2013 Effect of density stratification on vortex merger. Phys. Fluids 25 (1), 016601.CrossRefGoogle Scholar
Douady, S., Couder, Y. & Brachet, M. E. 1991 Direct observation of the intermittency of intense vorticity filaments in turbulence. Phys. Rev. Lett. 67 (8), 983–986.Google Scholar
Garten, J. F., Arendt, S., Fritts, D. C. & Werne, J. 1998 Dynamics of counter-rotating vortex pairs in stratified and sheared environments. J. Fluid Mech. 361, 189–236.CrossRefGoogle Scholar
Gottlieb, S., Shu, C.-W. & Tadmor, E. 2001 Strong stability-preserving high-order time discretization methods. SIAM Rev. 43 (1), 89–112.Google Scholar
Govindarajan, R. 2002 Universal behavior of entrainment due to coherent structures in turbulent shear flow. Phys. Rev. Lett. 88 (13), 134503.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kumar, B., Schumacher, J. & Shaw, R. A. 2013 Cloud microphysical effects of turbulent mixing and entrainment. Theor. Comput. Fluid Dyn. 27 (3–4), 361–376.Google Scholar
de Lozar, A. & Mellado, J.-P. 2014 Cloud droplets in a bulk formulation and its application to buoyancy reversal instability. Q. J. R. Meteorol. Soc. 140 (682), 1493–1504.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phy. Fluids 26 (4), 883–889.Google Scholar
Narasimha, R., Diwan, S. S., Duvvuri, S., Sreenivas, K. R. & Bhat, G. S. 2011 Laboratory simulations show diabatic heating drives cumulus-cloud evolution and entrainment. Proc. Natl Acad. Sci. USA 108 (39), 16164–16169.Google Scholar
Nomura, K. K., Tsutsui, H., Mahoney, D. & Rottman, J. W. 2006 Short-wavelength instability and decay of a vortex pair in a stratified fluid. J. Fluid Mech. 553, 283–322.Google Scholar
Orlandi, P., Egermann, P. & Hopfinger, E. J. 1998 Vortex rings descending in a stratified fluid. Phys. Fluids 10 (11), 2819–2827.Google Scholar
Pruppacher, H. R., Klett, J. D. & Wang, P. K. 1998 Microphysics of Clouds and Precipitation. Taylor & Francis.Google Scholar
Ravichandran, S., Dixit, H. N. & Govindarajan, R. 2017 Lift-induced vortex-dipole collapse. Phys. Rev. Fluids 2, 034702.Google Scholar
Ravichandran, S. & Govindarajan, R. 2015 Caustics and clustering in the vicinity of a vortex. Phys. Fluids 27 (3), 033305.Google Scholar
Rogers, M. C. & Morris, S. W. 2005 Buoyant plumes and vortex rings in an autocatalytic chemical reaction. Phys. Rev. Lett. 95 (2), 024505.Google Scholar
Rosa, B., Parishani, H., Ayala, O. & Wang, L.-P. 2016 Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution {DNS}. Intl J. Multiphase Flow 83, 217–231.Google Scholar
Saffman, P. G. 1972 The motion of a vortex pair in a stratified atmosphere. Stud. Appl. Maths 51 (2), 107–119.Google Scholar
Shaw, R. A., Reade, W. C., Collins, L. R. & Verlinde, J. 1998 Preferential concentration of cloud droplets by turbulence: effects on the early evolution of cumulus cloud droplet spectra. J. Atmos. Sci. 55 (11), 1965–1976.2.0.CO;2>CrossRefGoogle Scholar
Turner, J. S. 1957 Buoyant vortex rings. Proc. R. Soc. Lond. A 239 (1216), 61–75.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.CrossRefGoogle Scholar

Ravichandran supplementary movie

The movie shows the evolution of the four quantities (ω , θ , rv , rl) for the many-vortex case Re=5000, Stp=1, Sts=200. See figures 13–15 in the paper and corresponding text.

Download Ravichandran supplementary movie(Video)
Video 11.8 MB
Supplementary material: PDF

Ravichandran supplementary materials

Supplementary Materials

Download Ravichandran supplementary materials(PDF)
PDF 1.6 MB