Published online by Cambridge University Press: 11 July 2013
The flow structure and turbulence in an open cavity shear layer has been investigated experimentally at a Reynolds number of 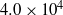 $4. 0\times 1{0}^{4} $, with an emphasis on interactions of the unsteady pressure field with the cavity corners. A large database of time-resolved two-dimensional PIV measurements has been used to obtain the velocity distributions and calculate the pressure by spatially integrating the material acceleration at a series of sample areas covering the entire shear layer and the flow surrounding the corners. Conditional sampling, low-pass filtering and time correlations among variables enable us to elucidate several processes, which have distinctly different frequency ranges, that dominate the shear layer interactions with the corners. Kelvin–Helmholtz shear layer eddies have the expected Strouhal number range of 0.5–3.2. Their interactions with the trailing corner introduce two sources of vorticity fluctuations above the corner. The first is caused by the expected advection of remnants of the shear layer eddies. The second source involves fluctuations in local viscous vorticity flux away from the wall caused by periodic variations in the streamwise pressure gradients. This local production peaks when the shear layer vortices are located away from the corner, creating a lingering region with peak vorticity just above the corner. The associated periodic pressure minima there are lower than any other point in the entire flow field, making the region above the corner most prone to cavitation inception. Flapping of the shear layer and boundary layer upstream of the leading corner occurs at very low Strouhal numbers of ∼0.05, affecting all the flow and turbulence quantities around both corners. Time-dependent correlations of the shear layer elevation show that the flapping starts in the boundary layer upstream of the leading corner and propagates downstream at the free stream speed. Near the trailing corner, when the shear layer elevation is low, the stagnation pressure in front of the wall, the downward jetting flow along this wall, the fraction of shear layer vorticity entrained back into the cavity, and the magnitude of the pressure minimum above the corner are higher than those measured when the shear layer is high. However, the variations in downward jetting decay rapidly with increasing distance from the trailing corner, indicating that it does not play a direct role in a feedback mechanism that sustains the flapping. There is also low correlation between the boundary/shear layer elevation and the returning flow along the upstream vertical wall, providing little evidence that this returning flow affects the flapping directly. However, the characteristic period of flapping, ∼0.6 s, is consistent with recirculation time of the fluid within the cavity away from boundaries. The high negative correlations of shear/boundary layer elevation with the streamwise pressure gradient above the leading corner introduce a plausible mechanism that sustains the flapping: when the shear layer is low, the boundary layer is subjected to high adverse streamwise pressure gradients that force it to widen, and when the shear layer is high, the pressure gradients decrease, allowing the boundary layer to thin down. Flow mechanisms that would cause the flapping-induced pressure changes, and their relations to the flow within the cavity are discussed.
$4. 0\times 1{0}^{4} $, with an emphasis on interactions of the unsteady pressure field with the cavity corners. A large database of time-resolved two-dimensional PIV measurements has been used to obtain the velocity distributions and calculate the pressure by spatially integrating the material acceleration at a series of sample areas covering the entire shear layer and the flow surrounding the corners. Conditional sampling, low-pass filtering and time correlations among variables enable us to elucidate several processes, which have distinctly different frequency ranges, that dominate the shear layer interactions with the corners. Kelvin–Helmholtz shear layer eddies have the expected Strouhal number range of 0.5–3.2. Their interactions with the trailing corner introduce two sources of vorticity fluctuations above the corner. The first is caused by the expected advection of remnants of the shear layer eddies. The second source involves fluctuations in local viscous vorticity flux away from the wall caused by periodic variations in the streamwise pressure gradients. This local production peaks when the shear layer vortices are located away from the corner, creating a lingering region with peak vorticity just above the corner. The associated periodic pressure minima there are lower than any other point in the entire flow field, making the region above the corner most prone to cavitation inception. Flapping of the shear layer and boundary layer upstream of the leading corner occurs at very low Strouhal numbers of ∼0.05, affecting all the flow and turbulence quantities around both corners. Time-dependent correlations of the shear layer elevation show that the flapping starts in the boundary layer upstream of the leading corner and propagates downstream at the free stream speed. Near the trailing corner, when the shear layer elevation is low, the stagnation pressure in front of the wall, the downward jetting flow along this wall, the fraction of shear layer vorticity entrained back into the cavity, and the magnitude of the pressure minimum above the corner are higher than those measured when the shear layer is high. However, the variations in downward jetting decay rapidly with increasing distance from the trailing corner, indicating that it does not play a direct role in a feedback mechanism that sustains the flapping. There is also low correlation between the boundary/shear layer elevation and the returning flow along the upstream vertical wall, providing little evidence that this returning flow affects the flapping directly. However, the characteristic period of flapping, ∼0.6 s, is consistent with recirculation time of the fluid within the cavity away from boundaries. The high negative correlations of shear/boundary layer elevation with the streamwise pressure gradient above the leading corner introduce a plausible mechanism that sustains the flapping: when the shear layer is low, the boundary layer is subjected to high adverse streamwise pressure gradients that force it to widen, and when the shear layer is high, the pressure gradients decrease, allowing the boundary layer to thin down. Flow mechanisms that would cause the flapping-induced pressure changes, and their relations to the flow within the cavity are discussed.