Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T19:40:28.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex separation and interaction in the wake of inclined trapezoidal plates

Published online by Cambridge University Press:  20 April 2015

Yuqi Huang ,
James Venning ,
Mark C. Thompson  and
John Sheridan
Yuqi Huang
Affiliation:
Power Machinery and Vehicular Engineering Institute, Department of Energy Engineering, Zhejiang University, Hangzhou 310027, China Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
James Venning*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Full three-dimensional numerical simulations are employed to investigate the flows over inclined trapezoidal low-aspect-ratio plates at low Reynolds numbers, aiming to understand the unsteadiness induced by the interaction between the trailing vortical wake structures originating from the swept edges, and those from the leading and trailing edges. The flows past eighteen different plate geometries in three broad sets are simulated to study the influence of aspect ratio, taper angle and angle of attack on the wake vortices and the force coefficients. Both taper ratio and angle of attack of plates with the same area are found to have a broadly predictable influence on the wake stability and asymptotic forces. Smaller taper ratios result in lower maximum lift, while an increase in the angle of attack results in a reduction in the differences in maximum lift. Two distinct modes of periodic unsteady flow with significant differences in frequency are observed. The corresponding vortex-shedding mechanisms are analysed with the aid of 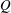$Q$-criterion isosurfaces and streamlines. A low wake frequency is observed at small taper angles when there is relative independence between the von Kármán vortices originating from the leading and trailing edges, and weak swept-edge vortices. The dominant Strouhal number in this state is approximately 0.09. When the taper angle or angle of attack increases, the flows over the swept edges form stronger trailing vortex structures which interact strongly with the leading-edge vortices, combining to produce a regular stream of vortex loops shed into the wake. In this regime, the dominant Strouhal number increases to approximately 0.14–0.18. Higher Reynolds numbers and/or angles of attack result in a loss of centre plane reflection symmetry in the wake. The aerodynamic forces have been quantified as a function of the problem parameters and plate geometry.

JFM classification

Vortex Flows: Vortex interactions Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 771 , 25 May 2015 , pp. 341 - 369
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afgan, I., Benhamadouche, S., Han, X., Sagaut, P. & Laurence, D. 2013 Flow over a flat plate with uniform inlet and incident coherent gusts. J. Fluid Mech. 720, 457–485.Google Scholar
Ahmed, S. R. 1981 An experimental study of the wake structures of typical automobile shapes. J. Wind Engng Ind. Aerodyn. 19, 49–62.Google Scholar
Ahmed, S. R., Ramm, G. & Faitin, G.1984 Some salient features of the time-averaged ground vehicle wake. Tech. Rep. Society of Automotive Engineers, Inc., Warrendale, PA.CrossRefGoogle Scholar
Birch, J. M. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl Biol. 207 (7), 1063–1072.Google Scholar
Blackburn, H. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15 (8), 57–60.Google Scholar
Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.Google Scholar
Chen, K. K., Colonius, T. & Taira, K. 2010 The leading-edge vortex and quasisteady vortex shedding on an accelerating plate. Phys. Fluids 22 (3), 033601.Google Scholar
Cooley, J. W. & Tukey, J. W. 1965 An algorithm for the machine calculation of complex Fourier series. Maths Comput. 19 (90), 297–301.Google Scholar
DeVoria, A. C. & Ringuette, M. J. 2012 Vortex formation and saturation for low-aspect-ratio rotating flat-plate fins. Exp. Fluids 52 (2), 441–462.Google Scholar
Dong, H., Mittal, R. & Najjar, F. M. 2006 Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 566, 309–343.Google Scholar
Gordnier, R. E. & Visbal, M. R.2003 Higher-order compact difference scheme applied to the simulation of a low sweep delta wing flow. In 41st Aerospace Sciences Meeting and Exhibition, 6–9 April, Reno, USA. AIAA.Google Scholar
Green, M. A., Rowley, C. W. & Smits, A. J. 2011 The unsteady three-dimensional wake produced by a trapezoidal pitching panel. J. Fluid Mech. 685, 117–145.Google Scholar
Gresham, N. T., Wang, Z. & Gursul, I. 2009 Low Reynolds number aerodynamics of free-to-roll low aspect ratio wings. Exp. Fluids 49 (1), 11–25.Google Scholar
Gursul, I., Gordnier, R. E. & Visbal, M. R. 2005 Aerodynamics of nonslender delta wings. Prog. Aerosp. Sci. 41, 515–557.Google Scholar
Hamdani, H. & Sun, M. 2000 Aerodynamic forces and flow structures of an airfoil in some unsteady motions at small Reynolds number. Acta Mechanica 145 (1–4), 173–187.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013a Relationship between aerodynamic forces, flow structures and wing camber for rotating insect wing planforms. J. Fluid Mech. 730, 52–75.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013b Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2014 The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight. J. Fluid Mech. 751, 71–105.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research.Google Scholar
Johnson, S. A., Thompson, M. C. & Hourigan, K. 2004 Predicted low frequency structures in the wake of elliptical cylinders. Eur. J. Mech. (B/Fluids) 23 (1), 229–239.Google Scholar
Khaledi, H. A., Narasimhamurthy, V. D. & Andersson, H. I. 2009 Cellular vortex shedding in the wake of a tapered plate at low Reynolds number. Phys. Fluids 21 (1), 013603.Google Scholar
Lam, K. M. & Leung, M. Y. H. 2005 Asymmetric vortex shedding flow past an inclined flat plate at high incidence. Eur. J. Mech. (B/Fluids) 24 (1), 33–48.Google Scholar
Lentick, D. & Dickinson, M. H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212 (16), 2705–2719.Google Scholar
Liu, Y.-C. & Hsiao, F.-B. 2012 Aerodynamic investigations of low-aspect-ratio thin plate wings at low Reynolds numbers. J. Mech. 28 (01), 77–89.Google Scholar
McQueen, T., Venning, J. & Sheridan, J.2014 Effects of aspect ratio on the wake dynamics of the Ahmed body. In Proceedings of the 19th Australasian Fluid Mechanics Conference, December 8–11, Melbourne, Australia.Google Scholar
Mittal, R. 1999 Planar symmetry in the unsteady wake of a sphere. AIAA J. 37 (3), 388–390.CrossRefGoogle Scholar
Najjar, F. M. & Balachandar, S. 1998 Low-frequency unsteadiness in the wake of a normal flat plate. J. Fluid Mech. 370, 101–147.Google Scholar
Narasimhamurthy, V. D., Andersson, H. I. & Pettersen, B. 2008 Cellular vortex shedding in the wake of a tapered plate. J. Fluid Mech. 617, 355–379.Google Scholar
Pitt Ford, C. W. & Babinsky, H. 2013 Lift and the leading-edge vortex. J. Fluid Mech. 720, 280–313.Google Scholar
Radi, A., Thompson, M. C., Sheridan, J. & Hourigan, K. 2013 From the circular cylinder to the flat plate wake: the variation of Strouhal number with Reynolds number for elliptical cylinders. Phys. Fluids 25 (10), 101706.Google Scholar
Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.Google Scholar
Saha, A. K. 2007 Far-wake characteristics of two-dimensional flow past a normal flat plate. Phys. Fluids 19 (12), 128110.Google Scholar
Saha, A. K. 2013 Direct numerical simulation of two-dimensional flow past a normal flat plate. J. Engng Mech. ASCE 139 (12), 1894–1901.Google Scholar
Sfakiotakis, M., Lane, D. M. & Davies, J. B. C. 1999 Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Engng 24 (2), 237–252.Google Scholar
Shields, M. & Mohseni, K. 2012 Effects of sideslip on the aerodynamics of low-aspect-ratio low-Reynolds-number wings. AIAA J. 50 (1), 85–99.Google Scholar
Taira, K. & Colonius, T. 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 623, 187–207.Google Scholar
Taira, K., Dickson, W. B. & Colonius, Tim. 2007 Unsteadiness in flow over a flat plate at angle-of-attack at low Reynolds numbers. In 45th AIAA Aerospace Sciences Meeting and Exhibition, January 8–11, Reno, USA, vol. 710.Google Scholar
Taira, K., Rowley, C. W., Colonius, T. & Williams, D. R. 2010 Lift enhancement for low-aspect-ratio wings with periodic excitation. AIAA J. 48 (8), 1785–1790.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006 Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22 (6–7), 793–806.Google Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.Google Scholar
Torres, G. E. & Mueller, T. J. 2004 Low-aspect-ratio wing aerodynamics at low Reynolds numbers. AIAA J. 42 (5), 865–873.Google Scholar
Venning, J., Lo Jacono, D., Burton, D., Thompson, M. & Sheridan, J. 2015 The effect of aspect ratio on the wake of the Ahmed body. Exp. Fluids (in press).Google Scholar
Viieru, D., Albertani, R., Shyy, W. & Ifju, P. G. 2005 Effect of tip vortex on wing aerodynamics of micro air vehicles. J. Aircraft 42 (6), 1530–1536.Google Scholar
Yang, D., Pettersen, B., Andersson, H. I. & Narasimhamurthy, V. D. 2011 Three-dimensional transition characteristics in the wake of an inclined flat plate. J. Phys.: Conf. Ser. 318 (3), 032044.Google Scholar
Zhang, J., Liu, N.-S. & Lu, X.-Y. 2009 Route to a chaotic state in fluid flow past an inclined flat plate. Phys. Rev. E 79 (4), 1–4.Google Scholar