Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T00:32:22.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex ring bifurcation and secondary structures in a finite-span synthetic jet

Published online by Cambridge University Press:  02 October 2020

Joseph C. Straccia  and
John A. N. Farnsworth Open the ORCID record for John A. N. Farnsworth [Opens in a new window]
Joseph C. Straccia
Affiliation:
Ann and H.J. Smead Department of Aerospace Engineering Sciences, University of Colorado Boulder, Boulder, CO80303, USA
John A. N. Farnsworth*
Affiliation:
Ann and H.J. Smead Department of Aerospace Engineering Sciences, University of Colorado Boulder, Boulder, CO80303, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

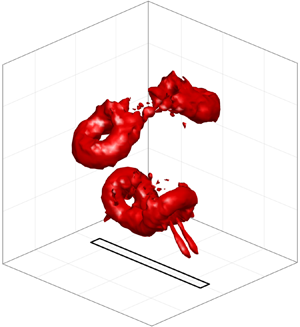
An experimental investigation using stereo particle image velocimetry (SPIV) was performed to study the vortex dynamics of an aspect ratio 13 rectangular orifice synthetic jet issuing into quiescent fluid. Data were obtained on the orifice centreline planes for four Reynolds numbers and five Strouhal numbers, ranging from 298 to 731 and 0.039 to 0.100, respectively. At one condition, SPIV data obtained on parallel planes distributed across the width of the jet were used to reconstruct the three-dimensional, three-component velocity field. The results reveal that the axis switching deformations of the non-circular vortex rings give rise to several types of secondary structures. Before the primary vortex ring completed its first axis switch, the anti-parallel sides of the ring collided, resulting in vorticity reconnection. Consequently, the elongated vortex ring bifurcated into two circular vortex rings which propagated off along independent paths. The development and structure of vortex ring bifurcation in addition to the bifurcation's effect on the jet shape, momentum and entrainment are presented. The bifurcation process captured in the synthetic jet experiment is similar in many ways to computational simulations of isolated vortex rings. Despite these similarities and the fact that vortex ring bifurcation was detected for all conditions tested, it is shown that the bifurcation process is sensitive to the unique conditions in synthetic jets, specifically the proximity of other vortex rings as indicated by the Strouhal number. Finally, the results at different jet conditions are discussed in relation to prior studies of synthetic jets.

JFM classification

Wakes/Jets: Jets Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A42
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adhikari, D. 2009 Some experimental studies on vortex ring formation and interaction. Master's thesis, National University of Singapore. Available at: http://scholarbank.nus.edu.sg/handle/10635/16569.Google Scholar
Afanasyev, Y. D. 2006 Formation of vortex dipoles. Phys. Fluids 18 (3), 037103.CrossRefGoogle Scholar
Amitay, M. & Cannelle, F. 2006 Evolution of finite span synthetic jets. Phys. Fluids 18 (5), 054101.CrossRefGoogle Scholar
Arms, R. J. & Hama, F. R. 1965 Localized-induction concept on a curved vortex and motion of an elliptic vortex ring. Phys. Fluids 8 (4), 553–559.CrossRefGoogle Scholar
Ashurst, W. T. & Meiron, D. I. 1987 Numerical study of vortex reconnection. Phys. Rev. Lett. 58 (16), 1632–1635.CrossRefGoogle ScholarPubMed
Belanger, R., Zingg, D. W. & Lavoie, P. 2020 Vortex structure of a synthetic jet issuing into a turbulent boundary layer from a finite-span rectangular orifice. AIAA Paper 2020-1815.CrossRefGoogle Scholar
Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
Chang, Y.-C., Lee, H.-W. & Tseng, H.-H. 2007 The formation of incense smoke. J. Aerosol Sci. 38 (1), 39–51.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Lim, T. T. 2016 Evolution of an elliptic vortex ring in a viscous fluid. Phys. Fluids 28 (3), 037104.CrossRefGoogle Scholar
Dhanak, M. R. & Bernardinis, B. D. E. 1981 The evolution of an elliptic vortex ring. J. Fluid Mech. 109, 189–216.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30 (1), 101–116.CrossRefGoogle Scholar
Domenichi, F. 2011 Three-dimensional impulsive vortex formation from slender orifices. J. Fluid Mech. 666, 506–520.CrossRefGoogle Scholar
Fohl, T. & Turner, J. S. 1975 Colliding vortex rings. Phys. Fluids 18 (4), 433–436.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.CrossRefGoogle Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12 (9), 1422–1429.CrossRefGoogle Scholar
Grinstein, F. F. 1995 Self-induced vortex ring dynamics in subsonic rectangular jets. Phys. Fluids 7 (10), 2519–2521.CrossRefGoogle Scholar
Grinstein, F. F. & DeVore, C. R. 1996 Dynamics of coherent structures and transition to turbulence in free square jets. Phys. Fluids 8 (5), 1237–1251.CrossRefGoogle Scholar
Grinstein, F. F., Fureby, C. & DeVore, C. R. 2005 On MILES based on flux-limiting algorithms. Intl J. Numer. Meth. Fluids 47 (10–11), 1043–1051.CrossRefGoogle Scholar
Grinstein, F. F., Margolin, L. G. & Rider, W. J., ed. 2007 Implicit Large Eddy Simulation. Cambridge University Press.CrossRefGoogle Scholar
Gutmark, E. J. & Grinstein, F. F. 1999 Flow control with noncircular jets. Annu. Rev. Fluid Mech. 31 (1), 239–272.CrossRefGoogle Scholar
Gutmark, E., Schadow, K. C., Parr, T. P., Hanson-Parr, D. M. & Wilson, K. J. 1989 Noncircular jets in combustion systems. Exp. Fluids 7 (4), 248–258.CrossRefGoogle Scholar
Ho, C.-M. & Gutmark, E. 1987 Vortex induction and mass entrainment in a small-aspect-ratio elliptic jet. J. Fluid Mech. 179, 383–405.CrossRefGoogle Scholar
Holman, R., Utturkar, Y., Mittal, R., Smith, B. L. & Cattafesta, L. 2005 Formation criterion for synthetic jets. AIAA J. 43 (10), 2110–2116.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88, pp. 193–208.Google Scholar
Husain, H. S. & Hussain, F. 1993 Elliptic jets. Part 3. Dynamics of preferred mode coherent structure. J. Fluid Mech. 248, 315–361.CrossRefGoogle Scholar
Hussain, F. & Husain, H. S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and excited jets. J. Fluid Mech. 208, 257–320.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kambe, T. & Takao, T. 1971 Motion of distorted vortex rings. J. Phys. Soc. Japan 31 (2), 591–599.CrossRefGoogle Scholar
Kida, S. & Takaoka, M. 1987 Bridging in vortex reconnection. Phys. Fluids 30 (10), 2911–2914.CrossRefGoogle Scholar
Kida, S., Takaoka, M. & Hussain, F. 1991 a Collision of two vortex rings. J. Fluid Mech. 230, 583–646.CrossRefGoogle Scholar
Kida, S., Takaoka, M. & Hussain, F. 1991 b Formation of head–tail structure in a two-dimensional uniform straining flow. Phys. Fluids A 3 (11), 2688–2697.CrossRefGoogle Scholar
Kiya, M. & Ishii, H. 1991 Deformation and splitting of pseudo-elliptical vortex rings. In Advances in Turbulence (ed. A.V. Johansson & P.H. Alfredsson), vol. 3. Springer.CrossRefGoogle Scholar
Kiya, M., Toyoda, K., Ishii, H., Kitamura, M. & Ohe, T. 1992 Numerical simulation and flow-visualization experiment on deformation of pseudo-elliptic vortex rings. Fluid Dyn. Res. 10 (2), 117–131.CrossRefGoogle Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
Lindstrom, A., Monastero, M. & Amitay, M. 2018 The flow physics of synthetic jets interaction with flow over a flapped airfoil. AIAA Paper 2018-4019.CrossRefGoogle Scholar
Lugt, H. J. 1996 Introduction to Vortex Theory. Vortex Flow Press.Google Scholar
Melander, M. V. & Hussain, F. 1988 Cut-and-connect of two antiparallel vortex tubes. Center for Turbulence Research Rep. CTR-S88, pp. 257–286.Google Scholar
Menon, S. & Soo, J. H. 2004 Simulation of vortex dynamics in three-dimensional synthetic and free jets using the large-eddy lattice Boltzmann method. J. Turbul. 5, 1–26.CrossRefGoogle Scholar
O'Farrell, C. & Dabiri, J. O. 2012 Perturbation response and pinch-off of vortex rings and dipoles. J. Fluid Mech. 704, 280–300.CrossRefGoogle Scholar
Oshima, Y. & Asaka, S. 1977 Interaction of two vortex rings along parallel axes in air. J. Phys. Soc. Japan 42 (2), 708–713.CrossRefGoogle Scholar
Oshima, Y., Izutsu, N., Oshima, K. & Hussain, A. K. M. F. 1988 Bifurcation of an elliptic vortex ring. Fluid Dyn. Res. 3 (1–4), 133–139.CrossRefGoogle Scholar
Pedrizzetti, G. 2010 Vortex formation out of two-dimensional orifices. J. Fluid Mech. 655, 198–216.CrossRefGoogle Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle image velocimetry: a practical guide. Experimental Fluid Mechanics. Springer.CrossRefGoogle Scholar
Sciacchitano, A., Neal, D. R., Smith, B. L., Warner, S. O., Vlachos, P. P., Wieneke, B. & Scarano, F. 2015 Collaborative framework for PIV uncertainty quantification: comparative assessment of methods. Meas. Sci. Technol. 26 (7), 074004.CrossRefGoogle Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.CrossRefGoogle Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.CrossRefGoogle Scholar
Van Buren, T., Whalen, E. & Amitay, M. 2014 b Vortex formation of a finite-span synthetic jet: high Reynolds numbers. Phys. Fluids 26 (1), 014101.CrossRefGoogle Scholar
Van Buren, T. & Amitay, M. 2016 Comparison between finite-span steady and synthetic jets issued into a quiescent fluid. Expl Therm. Fluid Sci. 75, 16–24.CrossRefGoogle Scholar
Van Buren, T., Beyar, M., Leong, C. M. & Amitay, M. 2016 Three-dimensional interaction of a finite-span synthetic jet in a crossflow. Phys. Fluids 28 (3), 037105.CrossRefGoogle Scholar
Van Buren, T., Whalen, E. & Amitay, M. 2014 a Vortex formation of a finite-span synthetic jet: effect of rectangular orifice geometry. J. Fluid Mech. 745, 180–207.CrossRefGoogle Scholar
Viets, H. & Sforza, P. M. 1972 Dynamics of bilaterally symmetric vortex rings. Phys. Fluids 15 (2), 230–240.CrossRefGoogle Scholar
Wang, L., Feng, L.-H., Wang, J.-J. & Li, T. 2018 a Evolution of low-aspect-ratio rectangular synthetic jets in a quiescent environment. Exp. Fluids 59 (6), 91.CrossRefGoogle Scholar
Wang, L., Feng, L.-H., Wang, J.-J. & Li, T. 2018 b Parameter influence on the evolution of low-aspect-ratio rectangular synthetic jets. J. Vis. 21 (1), 105–115.CrossRefGoogle Scholar
Wieneke, B. 2015 PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 26 (7), 074002.CrossRefGoogle Scholar
Zhao, Y. & Shi, X. 1997 Evolution of single elliptic vortex rings. Acta Mech. Sin. 13 (1), 17–25.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar

Straccia and Farnsworth supplementary movie

For movie description see pdf file

Download Straccia and Farnsworth supplementary movie(Video)
Video 9.4 MB
Supplementary material: PDF

Straccia and Farnsworth supplementary material

Caption for movie file

Download Straccia and Farnsworth supplementary material(PDF)
PDF 10.9 KB