Hostname: page-component-599cfd5f84-cdgjw Total loading time: 0 Render date: 2025-01-07T07:20:32.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex generation by deep-water breaking waves

Published online by Cambridge University Press:  08 October 2013

N. E. Pizzo  and
W. Kendall Melville
N. E. Pizzo*
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92093-0213, USA
W. Kendall Melville
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92093-0213, USA
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The connection between wave dissipation by breaking deep-water surface gravity waves and the resulting turbulence and mixing is crucial for an improved understanding of air–sea interaction processes. Starting with the ensemble-averaged Euler equations, governing the evolution of the mean flow, we model the forcing, associated with the breaking-induced Reynolds shear stresses, as a body force describing the bulk scale effects of a breaking deep-water surface gravity wave on the water column. 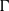From this, we derive an equation describing the generation of circulation, $\Gamma $, of the ensemble-average velocity field, due to the body force. By examining the relationship between a breaking wave and an impulsively forced fluid, we propose a functional form for the body force, allowing us to build upon the classical work on vortex ring phenomena to both quantify the circulation generated by a breaking wave and describe the vortex structure of the induced motion. Using scaling arguments, we show that 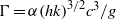$\Gamma = \alpha {(hk)}^{3/ 2} {c}^{3} / g$, where (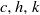$c, h, k$) represent a characteristic speed, height and wavenumber of the breaking wave, respectively, 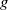$g$ is the acceleration due to gravity and $\alpha $ is a constant. This then allows us to find a direct relationship between the circulation and the wave energy dissipation rate per unit crest length due to breaking, 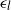${\epsilon }_{l} $. Finally, we compare our model and the available experimental data.

JFM classification

Geophysical and Geological Flows: Air/sea interactions Vortex Flows: Vortex Flows Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 734 , 10 November 2013 , pp. 198 - 218
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
©2013 Cambridge University Press.

References

Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian mean flow. J. Fluid Mech. 89, 609–646.CrossRefGoogle Scholar
Banner, M. L. & Peirson, W. L. 2007 Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 585, 93–115.Google Scholar
Banner, M. L. & Peregrine, D. H. 1993 Wave breaking in deep water. Annu. Rev. Fluid Mech. 25, 373–397.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Mechanics. Cambridge University Press.Google Scholar
Bühler, O. 2007 Impulsive fluid forcing and water strider locomotion. J. Fluid Mech. 573, 211–236.CrossRefGoogle Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
Csanady, G. T. 1994 Vortex pair model of Langmuir circulation. J. Mar. Res. 52, 559–581.Google Scholar
Dhanak, M. R. & De Bernardinis, B. 1981 The evolution of an elliptic vortex ring. J. Fluid Mech. 109, 189–216.CrossRefGoogle Scholar
Drazen, D. A., Melville, W. K. & Lenain, L. 2008 Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 611, 307–332.Google Scholar
Drazen, D. A. & Melville, W. K. 2009 Turbulence and mixing in unsteady breaking surface waves. J. Fluid Mech. 628, 85–119.CrossRefGoogle Scholar
Duncan, J . H. 1981 An experimental investigation of breaking waves produced by a towed hydrofoil. Proc. R. Soc. Lond. Ser. A 377, 331–348.Google Scholar
Duncan, J. H. 2001 Spilling breakers. Annu. Rev. Fluid Mech. 33, 519–547.Google Scholar
Hasselmann, K. 1974 On the spectral dissipation of ocean waves due to white capping. Boundary-Layer Met. 6, 107–127.Google Scholar
Helmholtz, H. 1858 Uber Integrale der hydrodynamischen Gleichungen welche den Wirbelbewe-gungen entsprechen. J. Reine Angew. Math. 55, 25–55.Google Scholar
Hornung, H. G., Willert, C. & Turner, S. 1995 The flow field of a hydraulic jump. J. Fluid Mech. 287, 299–316.Google Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2012 Fluid Mechanics, 5th edn. Academic.Google Scholar
Lamarre, E. & Melville, W. K. 1991 Air entrainment and dissipation in breaking waves. Nature 351, 469–472.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Leibovich, S. 1983 The form and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Linden, P. F. & Turner, J. S. 2001 The formation of optimal vortex rings, and the efficiency of propulsion devices. J. Fluid Mech. 427, 61–72.CrossRefGoogle Scholar
Longuet-Higgins, M. S & Turner, J. S. 1974 An entraining plume model of a spilling breaker. J. Fluid Mech. 63, 1–20.CrossRefGoogle Scholar
Melville, W. K. 1994 Energy dissipation by breaking waves. J. Phys. Oceanogr. 24, 2041–2049.2.0.CO;2>CrossRefGoogle Scholar
Melville, W. K. 1996 The role of wave breaking in air–sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.CrossRefGoogle Scholar
Melville, W. K. & Rapp, R. J. 1985 Momentum flux in breaking waves. Nature 317, 514–516.Google Scholar
Melville, W. K., Veron, F. & White, C. J. 2002 The velocity field under breaking waves: coherent structures and turbulence. J. Fluid Mech. 454, 203–233.CrossRefGoogle Scholar
Peregrine, D. H. 1998 Surf zone currents. Theor. Comput. Fluid Dyn. 10, 295–310.CrossRefGoogle Scholar
Peregrine, D. H. 1999 Large-scale vorticity generation by breakers in shallow and deep water. Eur. J. Mech. (B/Fluids) 18, 403–408.Google Scholar
Phillips, O. M. 1977 The Dynamics of the Upper Ocean, 2nd edn. Cambridge University Press.Google Scholar
Phillips, O. M. 1985 Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J. Fluid Mech. 156, 505–531.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rapp, R. J. 1986 Laboratory measurements of deep water breaking waves. PhD thesis, Ocean Engineering, Massachusetts Institute of Technology.Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331, 735–800.Google Scholar
Restrepo, J. M., Ramirez, J. M., McWilliams, J. C. & Banner, M. 2011 Multiscale momentum flux and diffusion due to whitecapping in wave–current interactions. J. Phys. Oceanogr. 41, 837–856.Google Scholar
Romero, L., Melville, W. K. & Kleiss, J. 2012 Spectral energy dissipation due to surface-wave breaking. J. Phys. Oceanogr. 42, 1421–1444.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2004 The oceanic boundary layer driven by wave breaking with stochastic variability. Part 1. Direct numerical simulations. J. Fluid Mech. 507, 143–174.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2007 Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 593, 405–452.Google Scholar
Sutherland, P., Melville, W. K., Lenain, L. & Statom, N. 2012 Measurements of near-surface wave coherent turbulence in the presence of breaking waves. The Oceanogr. Soc., the Am. Soc. of Lim. and Oceanogr. and the Am. Geophys. Union 2012 Ocean Sci. Meet., Abstract # 10699.Google Scholar
Tait, P. G. 1867 Translation of (Helmholtz 1858): On the integrals of the hydrodynamical equations, which express vortex-motion. Phil. Mag. 33, 485–512.Google Scholar
Taylor, G. I. 1953 Formation of a vortex ring by giving an impulse to a circular disk and then dissolving it away. J. Appl. Phys. 24, 104.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Tian, Z. G., Perlin, M. & Choi, W. 2010 Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mech. 655, 217–257.Google Scholar
Veron, F., Melville, W. K. & Lenain, L. 2009 Measurements of ocean surface turbulence and wave-turbulence interactions. J. Phys. Oceanogr. 39, 2310–2323.CrossRefGoogle Scholar
White, C. J. 1996 A laboratory study of breaking waves using digital particle image velocimetry. MS thesis, University of California, San Diego.Google Scholar